超聲振動珩磨作用下空化泡動力學及影響參數?

郭策　祝錫晶　劉國東　王建青　成全

（中北大學　機械與動力工程學院　太原　030051）

超聲振動珩磨作用下空化泡動力學及影響參數?

郭策?祝錫晶劉國東王建青成全

（中北大學機械與動力工程學院太原030051）

為了合理利用超聲振動珩磨作用下的空化效應，以磨削區單個空化泡為研究對象，考慮珩磨頭合成擾動速度和珩磨壓力的作用建立了磨削區空化泡的動力學模型。數值模擬了空化泡初始半徑，珩磨壓力，液體靜壓力和超聲聲壓幅值對磨削區空化效應的影響。研究表明考慮超聲振動珩磨作用時，空化泡膨脹的幅值會受到抑制，其潰滅時間也會縮短，而且較容易出現穩態空化。珩磨壓力和液體靜壓力對磨削區空化主要起抑制作用，超聲波聲壓幅值在一定范圍內能夠促進磨削區空化效果的提升。本文的研究為進一步理解超聲振動珩磨的空化機理提供了理論支持。

超聲振動，珩磨，空化泡，動力學

1　引言

超聲振動珩磨是功率超聲振動加工在精密及超精密加工領域的重要應用之一，該技術在脆硬性、難加工材料如38CrMnA、42MnCr52、NdFeB以及陶瓷材料的加工中取得了良好的效果［1-3］。超聲振動珩磨加工過程磨削區（由油石表面—切削液—工件內壁面組成的加工環境）會發生空化效應，產生大量的空化泡。

空化泡不穩定，不斷地生長、膨脹、壓縮乃至崩潰，其潰滅時還會產生局部的高溫高壓效應［4，5］。Rayleigh指出無粘性、不可壓縮液體中的空化泡崩潰會釋放沖擊波。Lauterborn等人利用高速攝影技術測得半徑約為500μm的空化泡，可以產生1 kPa的沖擊波［6］。Kornfeld和Suvorov認為空化泡可能是非軸對稱的潰滅，潰滅時會產生一束穿過氣泡的液體射流［7］。E.A.Brujan試驗測量近壁面空化泡產生的微射流可達1500 m/s［8］。由于空化的非線性振動，以及潰滅產生的沖擊波、微射流等效應，因此很容易對潛艇螺旋槳、水輪機和蒸汽機以及液體射流噴嘴產生腐蝕作用［9］，但與此同時，空化強大的破壞效應在功率超聲振動加工界如超聲清洗、超聲切割和超聲碎石等領域已引起足夠重視［10］，探討空化在功率超聲振動加工中的作用機理以及對空化泡的預測、控制和利用是進一步完善功率超聲加工理論的基礎。

描述氣泡的動力學規律可以用空化泡動力學模型來表示。目前，較為經典的模型是Rayleigh-Plesset模型，其它模型都是由該模型演變而得到的，包括較為著名的Keller-Miksis模型、Flynn模型、Prosperetti模型、Gilmore模型等等。作者前期對超聲振動珩磨磨削區空化聲場的分布及氣泡的輻射聲場進行過探討［11-12］。本文將在前期研究的基礎上，考慮珩磨頭合成擾動速度和珩磨壓力建立磨削區空化泡的動力學模型，同時也對影響超聲振動珩磨氣泡動力學特性的重要參數進行分析。

2　超聲振動珩磨磨削區氣泡動力學

2.1超聲振動珩磨的物理環境

珩磨加工是利用均勻分布在珩磨頭部的珩磨油石，通過漲心機構施加徑向的珩磨壓力ph從而將油石緊緊壓向缸套內壁。對于傳統珩磨，珩磨頭只進行往復和旋轉運動，而對于超聲振動珩磨，油石還被附加了超聲振動。超聲振動珩磨通常采用煤油或乳化液作為切削液，切削液以一定的流速及壓力經過噴嘴注入到磨削區，從而對珩磨加工過程起到冷卻和潤滑的作用。由于磨削區作用空間狹窄，逐漸注入到狹窄空間的切削液在珩磨頭速度ve的擾動下被分散成大量的微小的液滴和泡核，并存儲到油石及缸套內壁面的狹窄微空間內。

圖1為超聲振動珩磨的物理環境，設珩磨頭旋轉速度為v，往復速度為va，那么此時切削液受到珩磨頭的合成擾動速度ve為

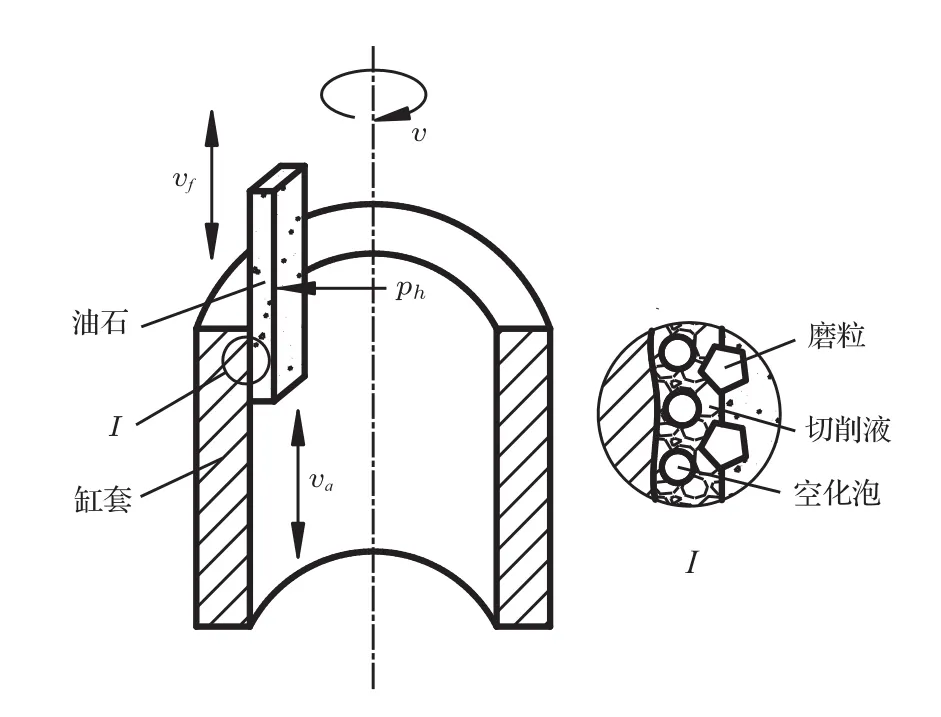
圖1　超聲振動珩磨加工過程的物理環境Fig.1 Physical environment of ultrasonic vibration honing in machining

超聲珩磨加工過程中，由于油石表面產生了高頻（18～22 kHz）及高幅（10～20μm）振動，油石表面、缸套內壁面的微觀縫隙、切削液中大量微小氣泡或泡核就會在超聲波的作用下被激活，并表現為迅速生長和膨脹，然后突然潰滅分裂成更多的小氣泡，也有可能表現為再次重復生長和崩潰的動力學過程。切削液初始流入磨削區時，受到的擾動較小，此時初生空化產生的氣泡表現為游移氣泡，而后隨著切削液在合成擾動速度ve的作用下，還可能產生類似于螺旋漿的梢渦空化。

2.2磨削區氣泡動力學模型

本文對氣泡假設如下：氣泡在運動過程中始終保持球形，而且球心固定；忽略氣泡自身重量；氣泡內的氣體近似為理想氣體；液體不可壓縮；考慮切削液的粘滯性和表面張力；不考慮氣泡振動在切削液傳播的輻射阻尼。那么，基于Rayleigh-Plesset方程的推導方法，切削液中的氣泡在外力W的作用下，轉化為氣泡的動能Ek和其它形式的能量ΔE，即

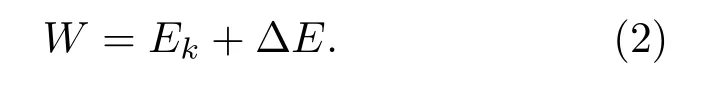
首先考慮到切削液中氣泡的動能Ek，

式中，Ek1為轉化為氣泡自身半徑變化的動能；Ek2為氣泡隨切削液一起流動的動能。那么，

式中，R為空化泡的半徑；r為距離氣泡中心的距離。

而外力對氣泡做功W為

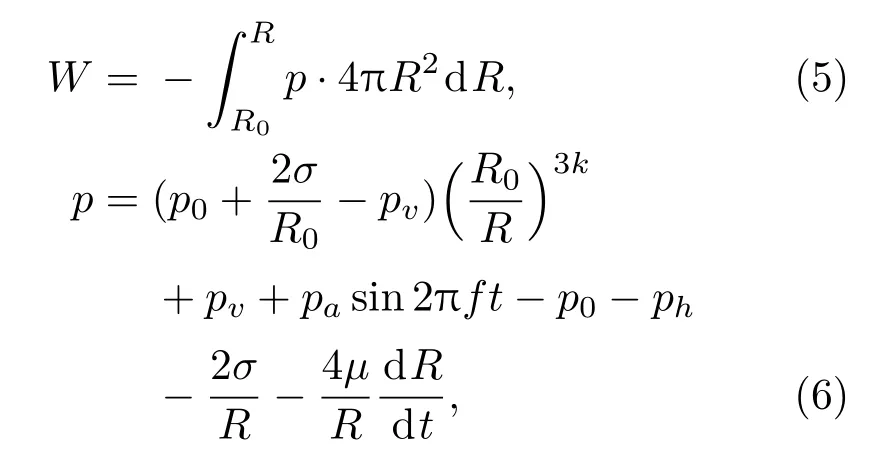
式中，p0為切削液靜壓力；R0為空化泡的初始半徑；σ為切削液表面張力系數；pa為聲壓幅值；pv為切削液的飽和蒸汽壓；f為超聲波頻率；ph為擠壓切削液的珩磨壓力；μ為切削液的粘滯系數；k為系數，當k=1時，泡內理想氣體為等溫過程；當k=γ時，視為絕熱過程，γ為氣體的絕熱指數（即氣體的等壓比熱與等容比熱之比）。

將式（4）～（6）代入式（2），忽略ΔE，就可以得到超聲振動磨削區氣泡的動力學模型如下：

2.3數值求解方法與初始條件

利用四階Runge-Kutta方法對式（3）進行數模擬，初始條件為：t=0時，R=R0，dR/dt=0。本文液體環境為煤油，其物理參數為：ρ=800 kg/m3，σ=0.024 N/m，μ=1.49 Pa·s，k=1.4。根據超聲珩磨的加工特點及工藝，f=20 kHz，v=πdn（d=47 mm，n=80 r/min），va=0.05 m/s［13］。

3　結果與討論

3.1氣泡初始半徑對氣泡運動的影響

強超聲作用下液體介質會出現許多不同尺度的氣泡，在同樣的聲波作用下，不同尺度氣泡雖然遵循相同的力學規律，但是振動行為并不相同。考慮超聲振動珩磨作用下切削液中的氣泡，顯然又會表現出新的變化規律。選擇p0=0.3 MPa，ph=0.4 MPa，pa=1.2 MPa，對R0為5μm、10μm、50μm、100μm的氣泡分別進行數值求解，得到氣泡無量綱位移隨時間的變化如圖2。對比圖2（a）、2（b）可以看出，當空化泡初始半徑較小如R0=5μm時，氣泡會在超聲作用下生長，膨脹至最大值后開始壓縮直至崩潰，而考慮超聲振動珩磨作用的氣泡膨脹的幅值較低、潰滅時間也較短。這說明考慮超聲振動珩磨作用時，氣泡膨脹的振動受到了抑制。隨著R0的逐漸增大，氣泡振動開始變的更為復雜，甚至經歷多個振蕩周期才潰滅。圖2（a）中當R0=10μm時，氣泡經歷三個聲周期才最終潰滅，而圖2（b）氣泡振動一個聲周期就完成了潰滅，對比氣泡首次壓縮的時間可以看出考慮超聲振動珩磨作用時，氣泡首次壓縮的時間更短。對于初始半徑較大的氣泡如R0=50、100μm，氣泡膨脹的幅值進一步降低，氣泡會經歷更多個聲周期振蕩才會潰滅，氣泡首次壓縮到最小的時間也會更長。

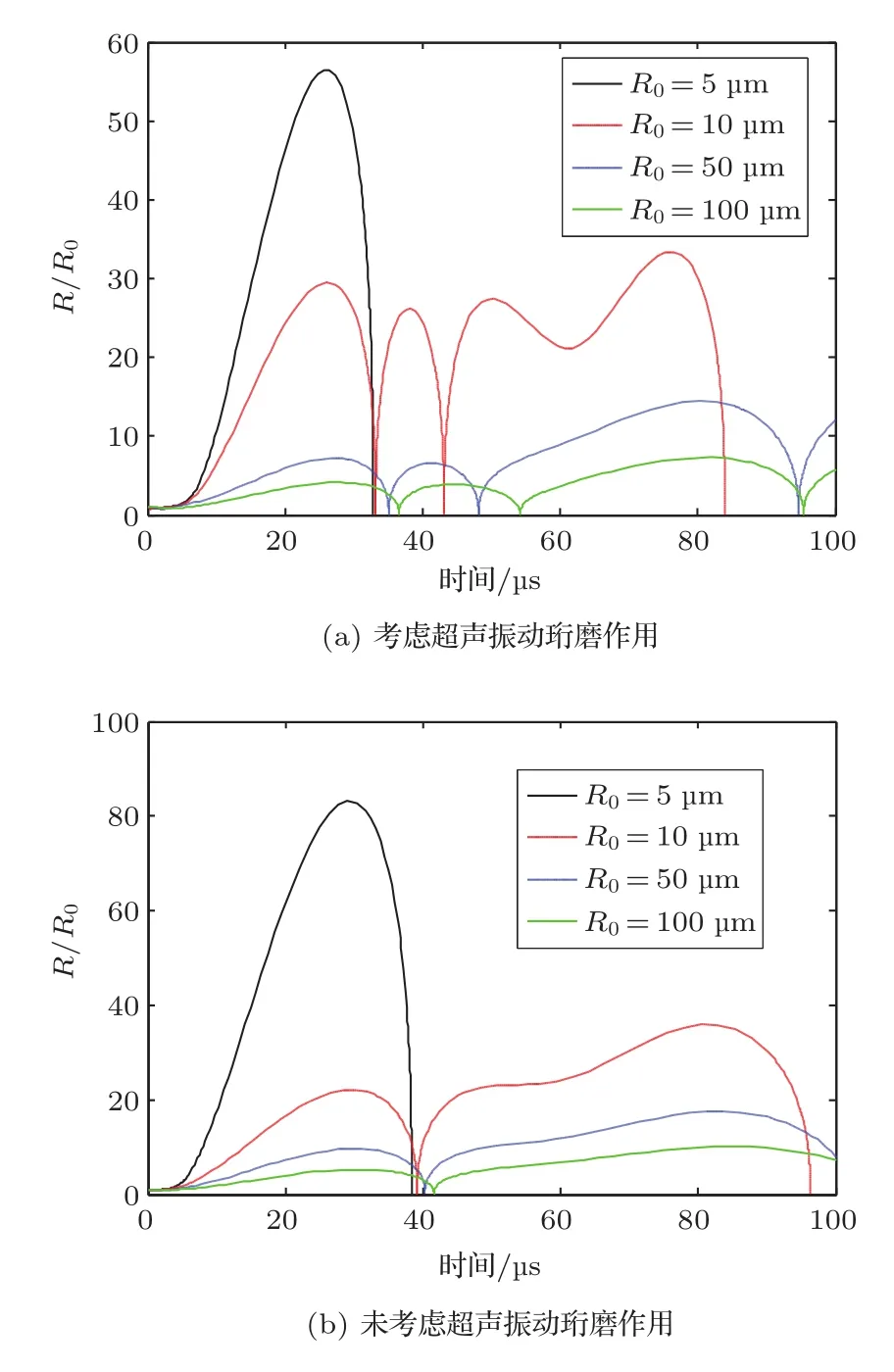
圖2　氣泡無量綱位移隨時間變化Fig.2 The dimensionless displacements of bubbles versus time

保持初始參數p0、ph、pa等參數不變，本文也對其它初始半徑空化泡的無量綱位移隨時間的變化進行了計算，得到結果如圖3。圖中縱坐標為氣泡最大膨脹幅值Rmax/R0與潰滅時間tcollapse，橫坐標為空化泡初始半徑。可以看出隨著R0的增大，Rmax/R0逐漸減少，特別是R0較小的時候，其Rmax/R0可以達到很高的值，但是當R0較大時，Rmax/R0甚至接近與零。而隨著R0的增大，其潰滅時間tcollapse近似于線性上升。對比圖3（a）、3（b）可以發現，考慮超聲振動珩磨作用時，空化泡的無量綱最大膨脹幅值Rmax/R0較低，而潰滅時間tcollapse也較短。

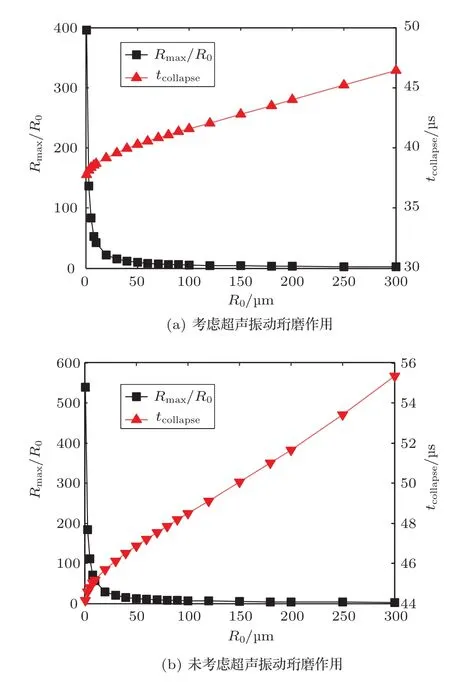
圖3　不同初始半徑空化泡的無量綱膨脹幅值與潰滅時間Fig.3　The dimensionless amplitude of bubble expansion and collapse time versus initial bubble radius

3.2珩磨壓力對氣泡運動的影響

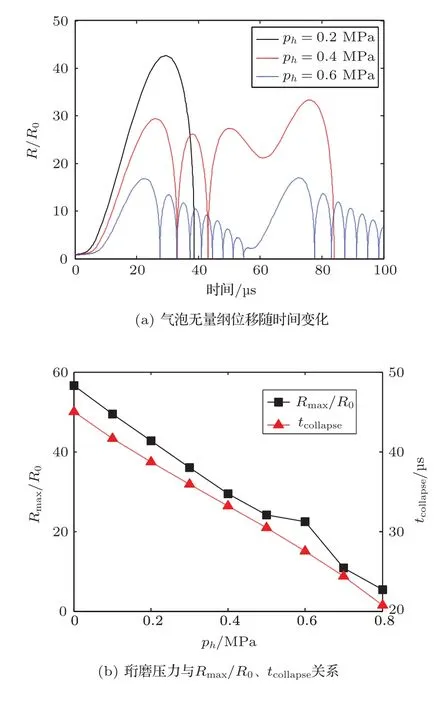
圖4　珩磨壓力對氣泡運動規律的影響Fig.4 Effect of honing pressure on bubble motion

超聲振動珩磨加工時，油石在珩磨壓力ph的作用下，將其表面的切削液緊緊地壓向材料表面，通過控制珩磨壓力可以間接的實現控制磨削區空化的強弱。選擇p0=0.3 MPa，pa=1.2 MPa，對R0=10μm的空化泡進行數值模擬，得到結果如圖4。圖4（a）表明，珩磨壓力較小時，空化泡直接潰滅如ph=0.2 MPa，當珩磨壓力逐漸增大時，空化泡開始變的不穩定，會振蕩多個周期才會發生潰滅如ph=0.4 MPa，當珩磨壓力增大到一定值時（本算例ph=0.6 MPa），空化泡會周期性的重復膨脹及壓縮的過程，近似于穩態空化。圖4（b）保持p0、pa等參數不變，給出了珩磨壓力與無量綱最大膨脹幅值Rmax/R0和潰滅時間tcollapse的關系。可以看出隨著珩磨壓力的增大，空化泡的無量綱最大膨脹幅值Rmax/R0會逐漸降低，而潰滅時間tcollapse（主要記錄的是氣泡首次壓縮到最小值的時間）也會縮短，這說明珩磨壓力對空化泡的振動更多的體現的是抑制的作用。值得注意的是當ph=0.6 MPa時，圖4（b）中Rmax/R0出現了短暫的跳動，而該值正是空化泡由瞬態轉變為穩態的臨界點，說明合理的控制珩磨壓力能夠更好的控制空化的強度及類型。實驗中發現當珩磨壓力增加到1.5～2 MPa的時候，超聲珩磨的磨削效果將不再增加。由于較高的珩磨壓力對機床本身的剛度及珩磨頭體的剛度都要求很高，除此之外，作者認為由于較高的珩磨壓力導致磨削區空化效果很微弱，而且主要以穩態空化為主，這也是超聲振動珩磨加工過程中不易選擇較高珩磨壓力的重要原因之一。

3.3液體靜壓力對氣泡運動的影響

超聲振動珩磨環境下，切削液由噴嘴注入到磨削區，通過控制噴嘴切削液的流速及壓力就可以控制液體靜壓力，從而控制切削液中的空化。選擇ph=0.2 MPa，pa=1.2 MPa，對初始半徑R0=10μm的空化泡進行數值模擬，得到結果如圖5。圖5（a）表明，液體靜壓力較小時，空化泡直接潰滅如p0=0.4 MPa；當液體靜壓力逐漸增大時，空化泡開始變的不穩定，會連續振蕩多個周期如p0=0.6 MPa時，空化泡在首次潰滅后經過多次反彈甚至反彈的幅值要超過首次膨脹的幅值，這主要與本文模型中忽略了液體可壓縮性及聲波向液體介質中傳播的阻尼所致。當液體靜壓力p0增大到0.8 MPa，空化泡開始進行周期性的重復膨脹及壓縮的過程，近似于穩態空化。保持ph、pa等參數不變，圖5（b）給出了液體靜壓力與無量綱最大膨脹幅值Rmax/R0和潰滅時間tcollapse的關系。可以看出隨著液體靜壓力的增大，空化泡的無量綱最大膨脹幅值Rmax/R0會逐漸降低，而潰滅時間tcollapse也會縮短，這說明液體靜壓力對于磨削區的空化也體現出抑制的作用。由于超聲波的聲壓幅值只有大于液體靜壓力才能在切削液中形成負壓，從而導致空化的初生，因此較大的液體靜壓力空化效果微弱甚至不產生空化。從式（10）也可以看出液體靜壓力p0與珩磨壓力ph協同對空化泡進行作用，因此二者共同改變切削液的壓力環境，在實驗中液體靜壓力可以通過噴嘴與流速進行控制，其壓力值主要維持在0.1～0.5 MPa之間。

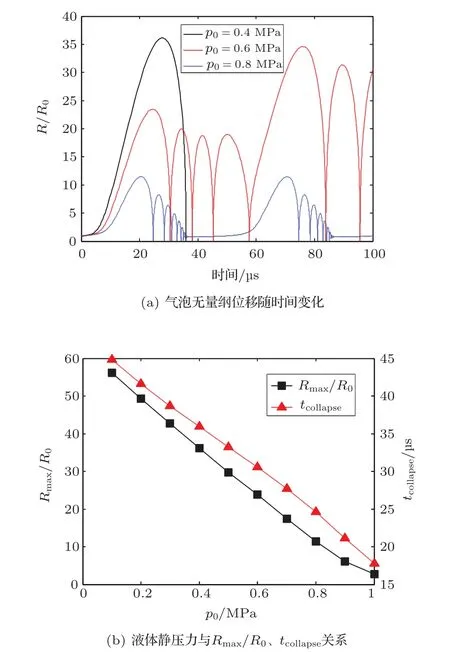
圖5　液體靜壓力對氣泡運動規律的影響Fig.5 Effect of hydrostatic pressure on bubble motion

3.4超聲波聲壓幅值對氣泡運動的影響

超聲振動珩磨加工時，超聲波聲壓幅值主要指的是油石表面產生的高幅振動，聲壓幅值的強度與超聲振動珩磨裝置結構，材料及超聲波性質有關，合理的控制超聲波聲壓幅值對于氣泡運動規律體現明顯。選擇ph=0.2 MPa，p0=0.3 MPa，對R0=10μm的空化泡進行數值模擬，得到結果如圖6。圖6（a）表明，超聲波聲壓幅值較小時，空化泡直接潰滅如pa=0.7 MPa；增大超聲波聲壓幅值時，空化泡會變得不穩定，會振蕩多個周期然后潰滅如pa=0.8 MPa，然而較大的超聲波聲壓幅值也會出現穩態空化的問題，如pa=1.5 MPa。保持ph、p0等參數不變，圖6（b）給出了超聲波聲壓幅值與無量綱最大膨脹幅值Rmax/R0和潰滅時間tcollapse的關系。可以看出隨著超聲波聲壓幅值的增大，空化泡的無量綱最大膨脹幅值Rmax/R0會逐漸增大，而潰滅時間tcollapse也會延長，但是當超聲波聲壓幅值較大時，其Rmax/R0和tcollapse增大的趨勢近似平緩，說明超聲波聲壓幅值控制在一定的范圍內，有助于空化效果的提升，當其值超過這一范圍時繼續增大超聲波聲壓幅值其空化效果將不再增強。由超聲波聲壓幅值的近似公式pa=ρcωA（式中：ρ為切削液的密度，c為超聲波在切削液中的傳播速度，ω為超聲波角頻率，A為超聲波振幅）可以看出，影響pa的因素較多，此外還會受到磨削區邊界條件的影響，特別是A和ω會受到超聲振動系統設計的限制，這些都使得pa并不利于加工過程中的調節，理論上主要控制在0.7～1.5MPa之間。如何在超聲振動珩磨過程中實現精確控制超聲波聲壓幅值將是超聲振動珩磨技術領域面臨的一大難題。

圖6　超聲波聲壓幅值對氣泡運動規律的影響Fig.6　Effect of acoustic amplitude on bubble motion

4　結論

研究超聲振動珩磨環境下磨削區氣泡的運動特性是超聲空化效應在機械領域的新應用。本文首先理論解釋了超聲振動珩磨環境下磨削區空化初生機理，通過考慮珩磨頭的合成擾動速度和珩磨壓力等因素對Rayleigh-Plesset模型進行了修正。通過分析發現：

（1）考慮超聲振動珩磨的作用，空化泡膨脹的幅值會受到抑制，其潰滅時間也會縮短，而且較容易出現穩態空化。

（2）珩磨壓力和液體靜壓力對磨削區空化泡的振動更多的體現的是抑制的作用，特別是合理的控制珩磨壓力能夠得到瞬態空化轉變為穩態空化的臨界點。

（3）超聲波聲壓幅值控制在一定的范圍內，有助于空化效果的提升，但當其值超過某一范圍時繼續增大超聲波聲壓幅值其空化效果將不再增強。

在工程實際應用過程中，磨削區還會受到極端環境如高溫、高壓以及大量脫落的切屑和磨粒的影響，故本文對磨削區空化泡的研究是基于理想液體的情況，為超聲振動珩磨實際加工提供必要的理論指導。

［1］ZHU X S，XU K W，ZHAO B，et al.Experimental and theoretical research on‘local resonance’in an ultrasonic honing system［J］.Journal of Materials Processing Technology，2002，129（1/2/3）：207-211.

［2］ZHU X J，WANG J Q，CHENG Q，et al.Research on dynamic grinding force in ultrasonic honing chatter［J］. Advances in Grinding and Abrasive Technology，2011，487：433-437.

［3］ZHU X J，WANG J Q，CHENG Q，et al.Radial power ultrasonic vibration honing friction analysis［J］.Solid State Phenomena：Application of Diamond and Related Materials，2011，175：183-186.

［4］莫潤陽，林書玉，王成會.超聲空化的研究方法及進展［J］.應用聲學，2009，28（5）：389-400. MO Runyang，LIN Shuyu，WANG Chenghui.Methods of study on sound cavitations［J］.J.Applied Acoustics，2009，28（5）：389-400.

［5］SOHRAB B，AMIN J S，WIRIA S，et al.Tawards classification of the bifurcation structure of a spherical cavitaion bubble［J］.Ultrasonics，2009，49（8）：605-610.

［6］LAUTERBOR W，KURZ T，GEISLESR R，et al.Acoustic cavitation bubble dynamics and sonoluminescence［J］. Ultrasonics Sonochemistry，2007，14（4）：484-491.

［7］KORNFELD D M，SUVOROV L.On the destructive action of cavitation［J］.Japanese Journal of Applied Physics，1944，15：495-506.

［8］BRUJAN E A，IKEDA T，MATSUMOTO Y.On the pressure of cavitation bubbles［J］.Experimental Thermal and Fluid Science，2008，32（5）：1188-1191.

［9］MAHDI M，EBRAHIMI R，SHAMS M.Numerical analysis of the effects of radiation heat transfer and ionization energy loss on the cavitation bubble’s dynamics［J］. Physics Letters A，2011，375（24）：2348-2361.

［10］TAKSHI N，MASATO I，MASATOSHI F.Cavitaion damage reduction by microbubble injection［J］.Nuclear Instruments and Methods in Physics Research A，2008，586（3）：382-386.

［11］郭策.功率超聲珩磨磨削區空化泡動力學及其輻射聲場［D］.太原：中北大學，2013.

［12］LIU G D，ZHU X J，GUO C.Research on modeling and simulation of cavitations sound field in the grinding zone of the power ultrasonic honing［J］.Acta Acoustica，2013，38（6）：663-668.

［13］祝錫晶.功率超聲振動珩磨技術的基礎與應用研究［D］.南京：南京航空航天大學，2007.

Dynamics of cavitation bubble and parameters under ultrasonic vibration honing?

GUO Ce?ZHU XijingLIU GuodongWANG JianqingCHENG Quan
（School of Mechanics and Power Engineering，North University of China city，Taiyuan 030051，China）

In order to make good use of the cavitation effect under power ultrasonic honing,based on a cavitation bubble in the grinding area,the dynamic model of cavitation bubble was established with consideration of ultrasonic honing velocity and honing pressure.The effect of initial bubble radius,honing pressure, hydrostatic pressure and acoustic amplitude on the cavitation in the grinding area was simulated numerically. The results show that taking the effect of ultrasonic vibration honing into account,the expansion of cavitation bubble is inhibited,the collapse time is reduced and it is easy to generate stable cavitation.The cavitation effect in the grinding area can be decreased by honing pressure and ambient hydrostatic,and increased by acoustic amplitude within a certain range.The study provides a theoretical support for further understanding the cavitation mechanism of ultrasonic vibration honing.

Ultrasonic vibration,Honing,Cavatation bubble,Dynamics

O427.4；TG580.67；N941.3s

A

1000-310X（2015）01-0051-07

10.11684/j.issn.1000-310X.2015.01.008

2014-04-16收稿；2014-06-14定稿

?國家自然科學基金項目（50975265，51275490），山西省研究生優秀創新項目（20143077）

郭策（1986-），男，山西懷仁縣人，博士研究生，研究方向：功率超聲振動加工技術。

E-mail：guoce1027@163.com