地聲參數及傳播損失不確定性估計與建模?

過武宏　笪良龍　趙建昕

（海軍潛艇學院　青島　266071）

地聲參數及傳播損失不確定性估計與建模?

過武宏?笪良龍趙建昕

（海軍潛艇學院青島266071）

地聲參數的不確定性對水聲傳播具有重要的影響。通過貝葉斯理論建立水聲環境不確定性推理模型，理論推導了地聲參數的似然函數以及地聲參數和傳播損失的后驗概率密度，并采用MCMC（Markov Chain Monte Carlo）進行了仿真計算，給出了地聲參數的二維后驗聯合概率密度和一維邊緣概率密度，在此基礎上對傳播損失的不確定性進行了估計，得到了傳播損失80%的可信區間。仿真和實驗結果表明，該方法適用于地聲參數反演和不確定性估計，并能獲取因地聲參數不確定性導致的傳播損失不確定性估計。

貝葉斯，后驗概率密度，地聲參數，馬爾可夫鏈蒙特卡洛

1　引言

海洋水體環境參數與海底地聲參數共同構成了水下聲傳播計算的環境參數，而地聲參數反演技術一直是水聲學中的熱門課題，然而現有的參數反演算法一般只給出參數的點估計，并且很少對參數的不確定性進行進一步描述。相比較而言貝葉斯推理能通過后驗概率密度給出整個模型參數的概率分布，所以采用優化算法容易丟失一些地聲參數反演問題解的重要信息，而對于具有多參數的模型，貝葉斯方法能用來對任何特定參數或參數的函數進行推理分析。有必要采用貝葉斯理論對水聲傳播模型中地聲參數估計與不確定性進行研究，獲取地聲參數的后驗概率密度，在此基礎上研究地聲參數不確定性對傳播損失的影響。

2　模型與算法

2.1水聲環境不確定性推理模型

將水聲環境觀測數據、地聲參數以及傳播損失劃分為三個域，如圖1［1-2］所示，它反映了從數據的觀測域d∈D到環境域m∈M，再到應用域u∈U的映射關系。這也說明了從海洋水聲觀測（觀測域）到傳播損失（應用域）估計的總體思路。地聲參數的估計作為中間步驟給出地聲參數的后驗概率分布p（m|d）（環境域）。在此基礎上，傳播損失的概率分布p（u|d）可由Monte Carlo求積獲得。由圖中可以看出，觀測數據d和應用域u都與m相關，并且由映射關系D（m）和U（m）相聯系，如果映射關系是唯一的，那么u=U（D-1（d））［3］。

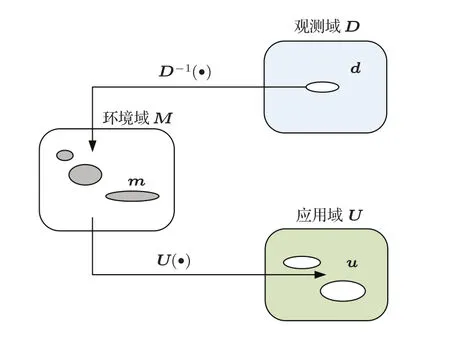
圖1　觀測域d∈D到環境域m∈M到應用域u∈U的映射關系圖［1-2］Fig.1　An observation d　∈　D is mapped into a distribution of environmental parameters m∈M that potentially could have generated it.　These environmental parameters are then mapped into the usage domain u∈U［1-2］

在貝葉斯統計方法中，認為總體分布中未知的環境參數向量m為隨機向量，在對m進行統計推斷時，需要對m設定一個先驗分布p（d|m），它是在獲得觀測數據前對于未知環境參數信息的概率表述。獲得觀測數據d之后，使用貝葉斯公式就可將參數的先驗分布更新為后驗分布。根據Bayesian理論，地聲參數的后驗分布、觀測信息、先驗分布之間有如下關系［1-2］：

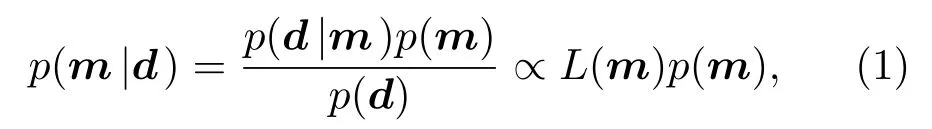
式中：p（d）為歸一化因子，由于觀測數據已經給出，它是一個與m無關的常數，可忽略；其中條件概率密度p（d|m）又稱似然函數，也可寫作L（m），表示估計的環境參數和實際的觀測數據的擬合程度，值越大表明擬合程度越高，反之越低。在此基礎上將先驗信息和觀測信息相結合，就可以得到反映未知的隨機環境參數向量m綜合信息的后驗概率密度p（m|d），它定義在整個解空間，表示了問題的“完全”解，而構造并計算p（m|d）是貝葉斯推論的核心問題。

2.2MCMC采樣方法

一旦獲得了參數的后驗分布，就可以獲得參數的任何特征，如單個參數的邊緣分布或均值、方差等［4］。然而除非對于很簡單的情況，后驗概率分布都不能以解析解的形式給出，所以必須采用數值積分方法。馬爾科夫鏈蒙特卡羅（MCMC）就是一種為了獲得參數后驗分布而發展起來，對復雜問題在高維空間上的數值積分方案。MCMC方法的基本原理就是基于建立的平穩分布為f（x）的Markov鏈來獲得f（x）的樣本。產生若干條獨立并行的Markov鏈來探索模型參數空間，通過不斷更新樣本信息而使Markov鏈收斂于高概率密度區，也就是Bayesian方法中的最大后驗估計。

根據Markov鏈所用轉移概率的不同，MCMC方法具有多種抽樣算法，如：Gibbs抽樣、Metropolis抽樣、Metropolis-Hastings抽樣［5-7］。本文采用目前較為常用的Metropolis-Hastings算法，其算法流程如下：

（1）t=1，將初值賦給不同變量；

（2）while t＜T

（a）t=t+1；

（b）產生服從建議分布的推薦變量值m?；

（c）計算接受概率

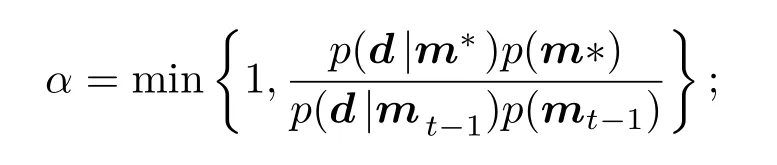
（d）產生服從均勻分布的隨機數u～U（0，1）；

（e）若u＜α，則mt=m?，否則mt=mt-1；

（3）重復第（2）步（a）～（e），直到產生T個樣本為止。

3　似然函數與后驗概率密度

3.1似然函數

若觀測的數據矢量表示為d=D（m）+e，式中D（m）=d（m）s，其中s表示聲源信息，且e是服從均值為0，協方差為Ce正態分布的誤差項，則似然函數為［2］

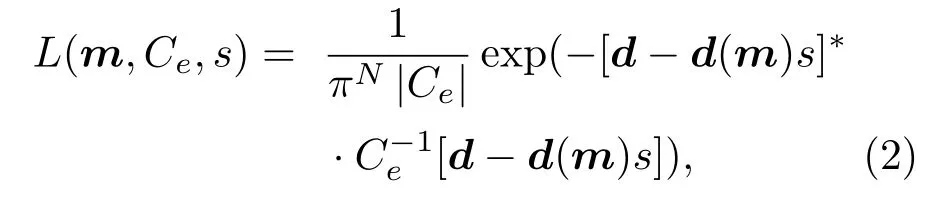
式中：N為數據點的數量，上標?表示共軛轉置，轉換函數d（m）由水聲傳播模型獲得。用獨立同分布的誤差Ce=vI來描述數據的不確定性，其中v為誤差方差，那么當?lgL/?s=0時

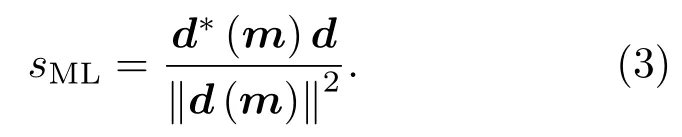
將式（3）代入公式（2），似然函數則變為

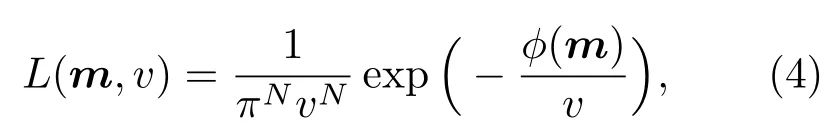
式中

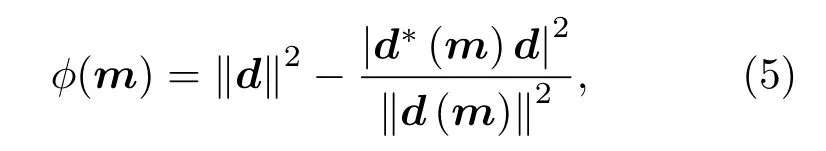
為目標函數。在此，將誤差方差視為冗余參量并通過對公式（4）求積消除v，那么

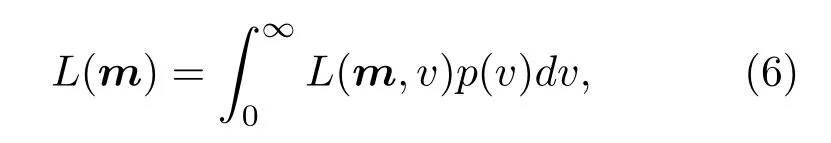
式中p（v）=1/v［2］。至此，似然函數可寫為［2］

3.2地聲參數與傳播損失的后驗概率密度

獲得地聲參數的似然函數L（m），結合參數相應的先驗信息，便可求得環境參數的后驗概率密度p（m|d）。而對于利用水聲環境來說，傳播損失（TL）與聲納探測性能估計直接相關，在模型中用u表示，它可表示為I個離散位置的傳播損失，即ui=u（ri，zi），i=1，···，I，其中ri和zi分別表示距離和深度上的離散值。那么傳播損失的后驗概率密度p（u|d）可由u和m的聯合概率密度函數獲得［2］

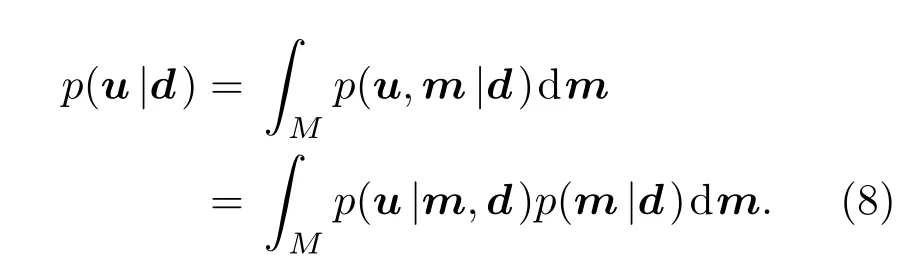
假設所有的不確定性均在數據域d中，并且數據域d中所有的信息都被映射到水聲環境域m，那么

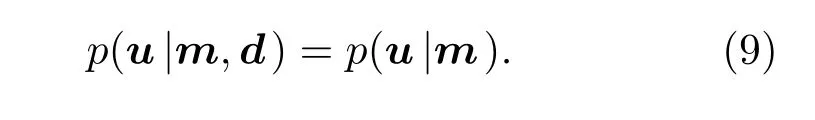
條件概率密度函數p（u|m）用于描述環境知識的不完全情況下，前向映射的不確定性。假設水聲傳播模型是準確的，函數關系表示為ui=Ui（m），i=1，···，I，簡記為u=U（m），這樣對于每一個環境值m，都能給出一個較為準確的傳播損失u。此時概率密度可寫為

如圖2所示，直角部分可以采用兩條Clothoid曲線A0和A1過渡，曲線A0和A1分別起始于點P0與P1，相遇于P，在起始點處與直線曲率相同為0，在點P兩條曲線曲率相同并且切線平行反向，這樣保證了整條運動軌跡曲率G2連續。

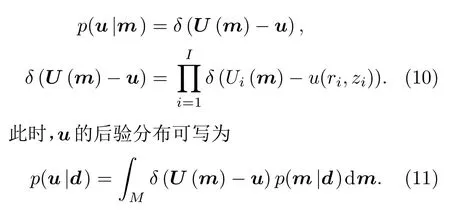
MCMC方法對于Bayesian推論問題較為適用，公式（12）中的積分即δ（U（m）-u）的期望函數，可采用蒙特卡洛積分方法求解，該方法關鍵在于獲得服從復雜目標分布的大量樣本，而MCMC方法可對模型參數后驗分布p（m|d）進行Metropolis-Hastings抽樣{m（t）}來近似。

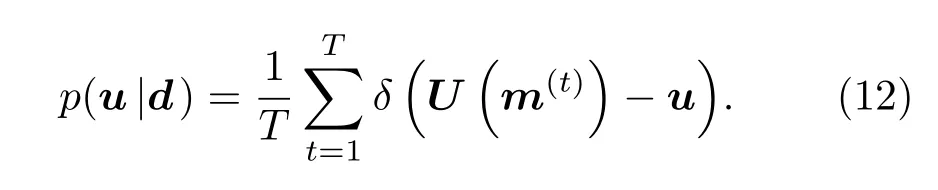
至此，我們便得到了傳播損失，即應用域u的分布，即傳播損失的概率分布，它包含了水聲環境參數估計的不確定性。為了更好的描述傳播損失的不確定性情況，在此采用后驗預測概率分布50%處的中值u50%和β1%處與β2%處之間的區域［uβ1%，uβ2%］來描述傳播損失分布。通過滿足下式進行求解：

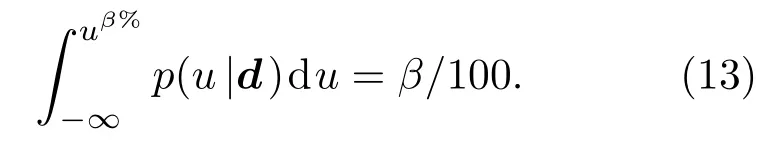
根據地聲環境參數不確定性程度及其傳播損失后驗預測概率分布公式，本文β1、β2分別取10與90，并以β2%與β1%之間的范圍表示傳播損失估計范圍，把其稱為傳播損失（β2-β1）%的可信區間（Credibility interval）。

4　實驗與算例

4.1實驗概況

2012年6月30日在黃海北部某海域進行了水聲傳播實驗，實驗過程及水聽器布放如圖2所示，接收船靜止布放16元垂直陣，水聽器之間距離2 m，發射船以10節速度遠離接收船，每隔1 min投放一枚手榴彈作為爆炸聲源，接收船接收爆炸聲信號，實驗海區聲速剖面如圖3所示。實驗數據獲取與處理參見文獻［8］。

圖3　實驗海區聲速剖面Fig.3 Sound speed profile in experimental area

海洋環境模型是進行地聲環境參數及其不確定性估計的基礎。目前，國內外估計淺海水聲環境參數時大都采用分層的海底模型，其中兩層海底模型應用最多。根據淺海水聲環境參數估計的特點及試驗所在海區的底質情況，采用兩層海底模型，如圖2所示。考慮待估的地聲環境參數為7個，分別為：沉積層密度rhos（g/cm3）、巖石層密度rhor（g/cm3）、沉積層聲速Csed（m/s）、巖石層聲速Crock（m/s）、沉積層厚度Dsed（m）、巖石層厚度Drock（m）、沉積層衰減alphy（dB/λ）。推理模型中的映射關系D（m）和U（m）采用KRAKEN簡正波傳播模型。各參數的先驗分布，根據參數的取值范圍設定為截斷正態分布，沉積層密度、聲速的均值根據海圖標注的底質給出經驗取值。各參數初始取值分別為：1.83 g/cm3、2.5 g/cm3、1677 m/s、1850 m/s、4 m、15 m、0.1 dB/λ。

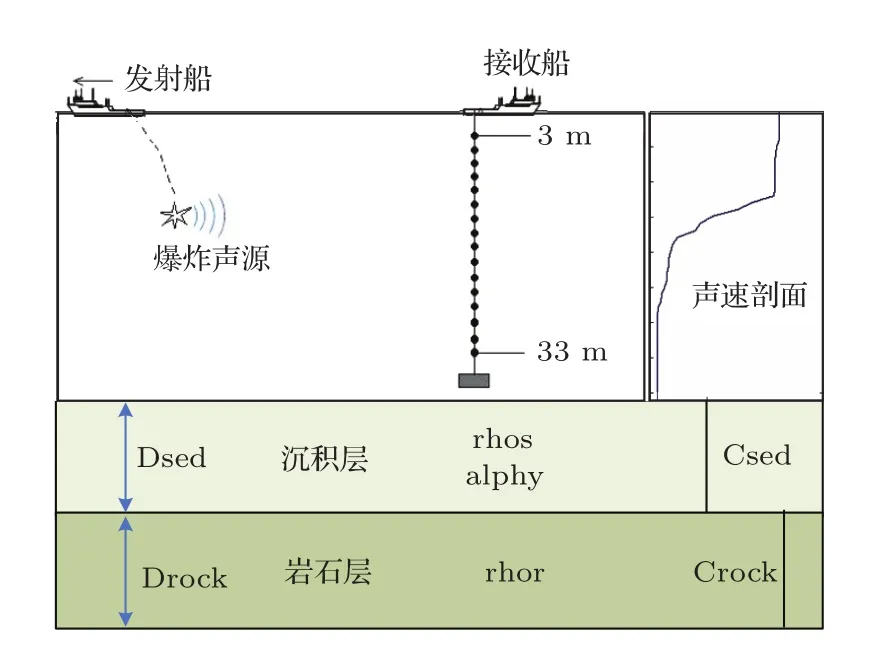
圖2　實驗示意圖及淺海環境模型Fig.2　Schematic diagram of experiment and shallow water model

4.3結果分析

仿真計算時采用聲源頻率100 Hz，各參數的二維后驗概率密度分布如圖4所示，其中顏色越亮代表后驗概率密度值越高，它表達了各參數在二維空間中的取值范圍。同時，圖5給出了各參數一維的后驗概率密度分布圖，表1給出了各地聲參數后驗概率密度的均值與均方差。從結果可以看出，采用MCMC方法獲得的地聲參數后驗概率密度可以對先驗知識進行修正，而其中因沉積層衰減對模型計算的敏感程度較高，后驗估計對先驗信息有較大的改善。從圖中也可以看出，與以往地聲參數反演問題的點估計相比，本文給出了參數的概率密度分布，包含的參數信息也更全面。

根據水聲環境不確定性推理模型，得出地聲參數的后驗概率密度可作為傳播損失不確定性估計的中間步驟，由公式（13）便可求得傳播損失的后驗概率密度，并根據公式（14）求得某一距離上滿足一定概率的傳播損失區間。

如圖6、7所示，分別是接收深度13 m和31 m時傳播損失的不確定性估計，其中（a）、（b）為10 km以內，傳播損失的均值（中間紅色實線）與80%的可信區間（兩條黑色虛線之間的區間）；（b）和（c）分別是3 km和8 km處傳播損失的概率密度直方圖。從圖中可以看出以上兩個深度傳播損失的實驗數據（“*”表示）均落于80%的可信區間，而且從傳播趨勢以及均方差可以看出，距離聲源越遠，不確定性越大。

圖4　地聲環境參數二維后驗概率密度Fig.4 2D posterior probability densities of geoacoustic parameters

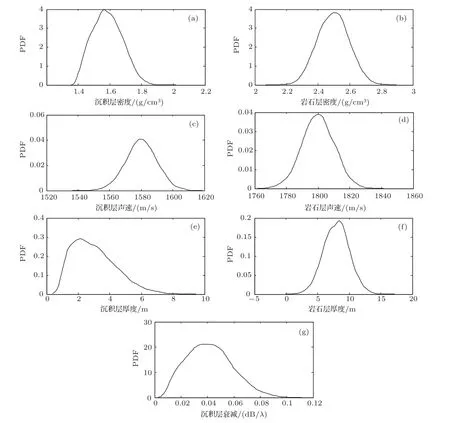
圖5　地聲環境參數一維邊緣后驗概率密度Fig.5 1D marginal posterior probability densities of geoacoustic parameters

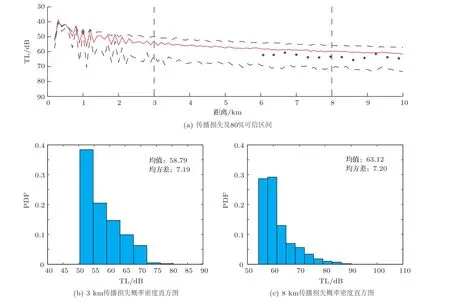
圖6　接收深度13 m時的傳播損失不確定性Fig.6 Uncertainty of transmission loss（TL）at 13 m depth

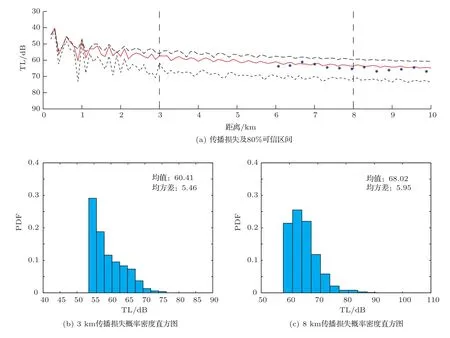
圖7　接收深度31 m時的傳播損失不確定性Fig.7 Uncertainty of transmission loss（TL）at 31 m depth

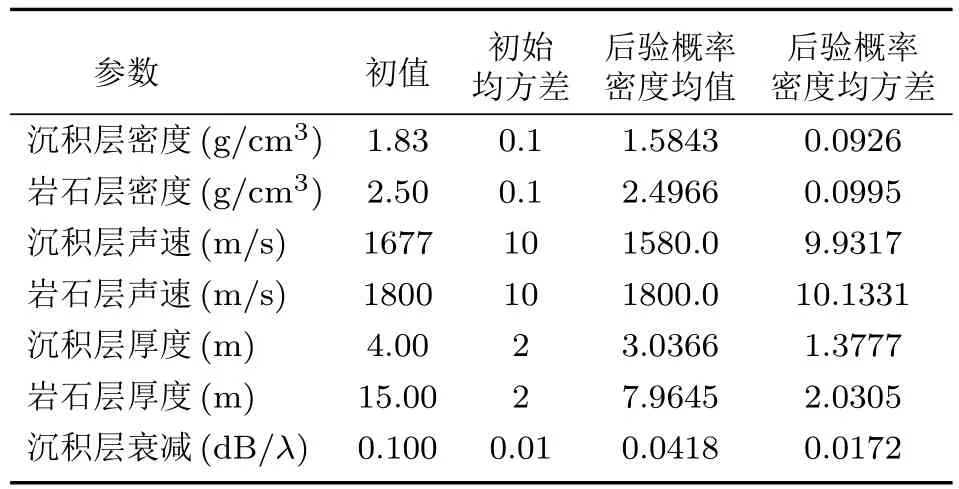
表1　地聲參數后驗概率密度均值與均方差Table 1　Mean value and mean square deviation of geoacoustic parameters posterior probability densities mean

同理，其他深度上傳播損失的均值與80%的可信區間如圖8所示，從圖中可以看出除表層（7 m、9 m）和躍層中下深度（23 m、25 m、27 m）的實驗數據與計算數據吻合程度相對較差，其余深度的實驗數據均落在傳播損失80%的可信區間之內。這是因為靠近海面的水聽器受海面影響較大，數據的質量相對較低，而23～27 m正好是躍層向均勻層過渡的深度，受躍變層不穩定性和海底因素等影響較大，因此計算的傳播損失區間與實驗數據有一定出入。

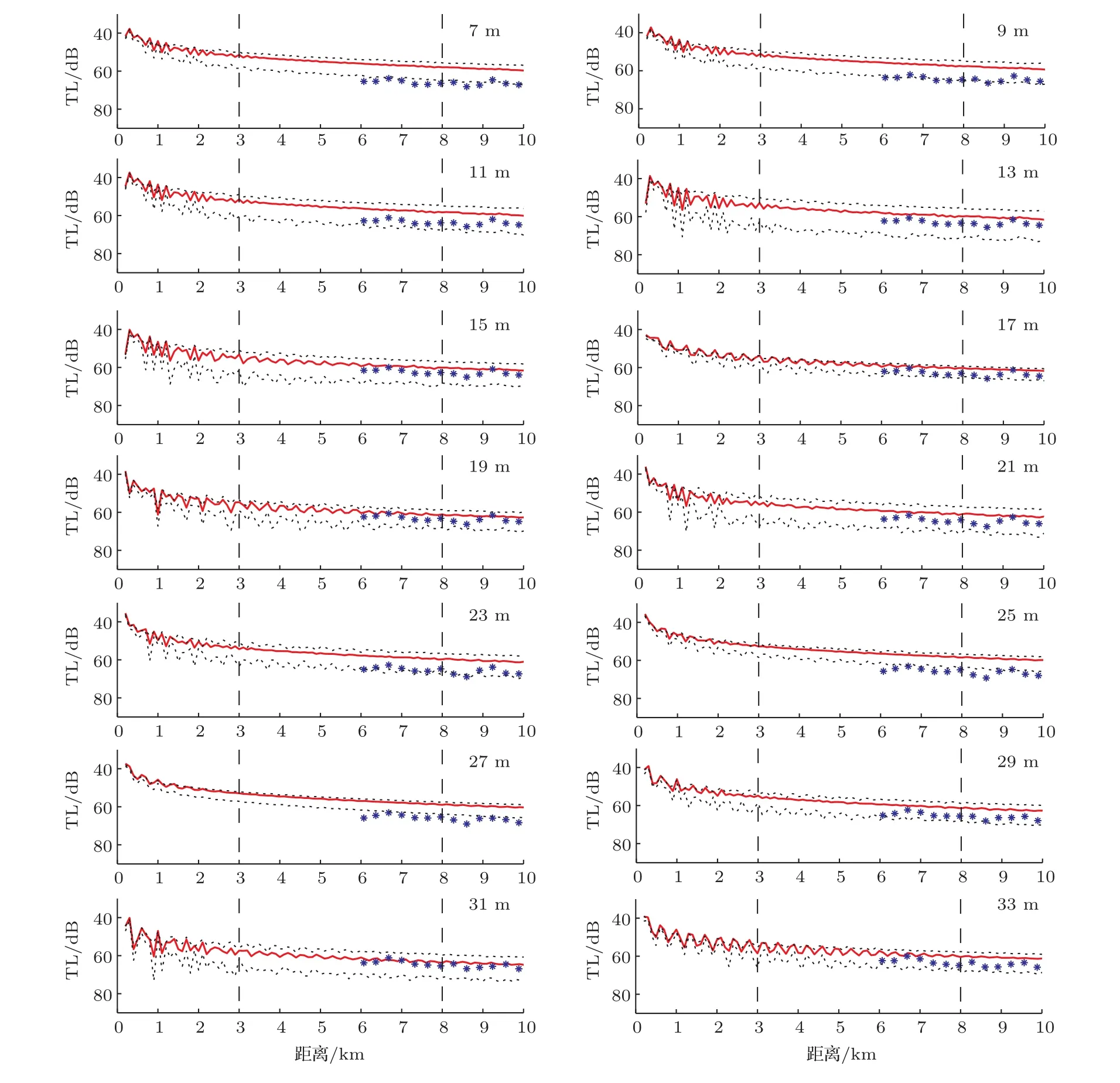
圖8　不同接收深度時傳播損失的80%可信區間與實驗數據對比Fig.8 Predicted and measured TL and its 80%credibility interval at different depth

5　結論

本文首先通過貝葉斯理論建立水聲環境不確定性推理模型，介紹了MCMC算法，推導了地聲參數的似然函數以及地聲參數和傳播損失的后驗概率密度，采用2012年黃海北部某海域水聲傳播實驗數據反演了地聲參數的后驗概率密度，并在此基礎上對傳播損失的不確定性進行了估計，得到了傳播損失80%的可信區間。經與實驗數據對比，驗證了該方法對地聲參數的不確定性估計具有一定的優勢，與已有的地聲參數反演與水聲不確定性研究相比，本文的主要改進之處在于將先驗信息和觀測信息相結合，得到反映地聲參數向量綜合信息的后驗概率密度，已有的地聲參數反演是在選定的變化范圍根據觀測數據進行尋優計算使代價函數達到最小值，來確定地聲參數，這里計及環境參數的隨機因素，應用概率統計方法獲取地聲參數后驗概率密度均值表征反演后的取值概率，比較科學。并應用到與環境參數密切相關的傳播損失的不確定性的估計，表示了問題的“完全”解。但是該方法計算效率相對較低，在抽樣算法方面還可進行進一步的深入研究。

［1］GERSTOFT P，HUANG C F，HODGKISS W S.Estimation of transmission loss in the presence of geoacoustic inversion uncertainty［J］.IEEE Journal of Ocean Engineering，2006，31（2）：299-307.

［2］HUANG C F，GERSTOFT P，HODGKISS W S.Validation of statistical estimation of transmission loss in the presence of geoacoustic inversion uncertainty［J］.Journal of Acoustical Society of America，2006，120（4）：1932-1941.

［3］笪良龍.海洋水聲環境效應建模與應用［M］.北京：科學出版社，2012：131-134. DA Lianglong.Ocean acoustic environment modeling and application［M］.Beijing：Science Press，2012：131-134.

［4］朱嵩，毛根海，程偉平，等.基于貝葉斯推理的水環境系統參數識別［J］.江蘇大學學報（自然科學版），2007，28（3）：237-240. ZHU Song，MAO Genhai，CHENG Weiping，et al.Parameters identification for water environmental system based on Bayesian inference［J］.Journal of Jiangsu University（Natural Science Edition），2007，28（3）：237-240.

［5］PENG R H，CHEN R R，FARHANG-BOROUJENY B. Markov Chain Monte Carlo detectors for channels with intersymbol interference［J］.IEEE Transactions on Signal Processing，2010，58（4）：2206-2217.

［6］SPALL J C.Estimation via Markov Chain Monte Carlo［J］. IEEE Control Systems Magazine，2003，23（2）：34-45.

［7］JOSEPH L S，RECAI M Y.Computational strategies for multivariate linear mixed-effects models with missing values［J］.Journal of Computational and Graphical Statistics，2002，11（2）：437-457.

［8］過武宏，笪良龍，趙建昕.動態水聲環境不確定性的估計與分析［J］.應用聲學，2013，32（6）：464-472. GUO Wuhong，DA Lianglong，ZHAO Jianxin.Uncertainty estimation and analysis for dynamic underwater acoustic environment［J］.Applied Acoustics，2013，32（6）：464-472.

Estimation and modeling of geoacoustic parameters and transmission loss uncertainty?

GUO Wuhong?DA LianglongZHAO Jianxin
（Navy Submarine Academy，Qingdao 266071，China）

Uncertainty of geoacoustic parameters has a great effect on acoustic propagation.In this paper,the uncertainty inference model of the acoustic environment is established via Bayes theorem.Then the likelihood function of the geoacoustic parameters and the posterior probability distribution of the geoacoustic parameters and transmission loss are deduced.Furthermore,a simulation is made using Markov Chain Monte Carlo（MCMC）.Two-dimensional and one-dimensional posterior probability densities of the geoacoustic parameters are given.Meanwhile,the uncertainty of transmission loss is estimated.The mean and 80%credibility interval of transmission loss in different depths are given.The results of the simulation and experiments show that the method is good at geoacoustic parameters inversion and uncertainty estimation,and it can get the uncertainty estimation of the transmission loss that is caused by uncertainty of the geoacoustic parameters.

Bayesian，Posterior probability density，Geoacoustic parameters，Markov Chain Monte Carlo

TP391

A

1000-310X（2015）01-0071-08

10.11684/j.issn.1000-310X.2015.01.011

2014-01-18收稿；2014-05-10定稿

?中國博士后科學基金項目（20110491884），總裝預研基金項目（9140A03060213JB15039）

過武宏（1980-），男，浙江杭州人，博士后，研究方向：海洋、水聲環境預報與不確定性。

E-mail：g1w2h31980@163.com