關節(jié)軸承摩擦溫度場計算方法

俞建衛(wèi)　王禮飛　魏　巍

合肥工業(yè)大學，合肥，230009

關節(jié)軸承摩擦溫度場計算方法

俞建衛(wèi)王禮飛魏巍

合肥工業(yè)大學，合肥，230009

以推力型關節(jié)軸承為研究對象，分析了軸向載荷下的接觸應力，并根據(jù)試驗所得摩擦力矩反推出了動態(tài)摩擦因數(shù)。結合接觸應力及摩擦因數(shù)求出了摩擦熱流率，并將其作為第二類邊界條件進行了軸承非定常溫度場有限元分析，最后利用紅外熱像儀拍攝了摩擦過程中軸承側表面溫度分布，檢驗仿真結果的可靠性。仿真與試驗結果表明：該計算方法解決了球面摩擦副摩擦因數(shù)的精確計算和熱流率的空間分配問題，建模時忽略球面間隙會直接影響接觸應力分布并造成溫度場分布出現(xiàn)較大誤差，考慮球面間隙可以更精確地計算軸承摩擦溫度場。

關節(jié)軸承；球面間隙；接觸應力；溫度場；紅外測量；有限元

0　引言

關節(jié)軸承又稱球面滑動軸承，是一種摩擦副為球面的特殊滑動軸承，常在重負荷條件下做低速擺動或旋轉，在軍用機械、建筑及航空等眾多領域均有大量應用[1-3]。潤滑型關節(jié)軸承材料多數(shù)使用GCr15鋼,采用淬火后低溫回火處理[4],當使用溫度高于回火溫度時,材料硬度急劇下降,材料磨損加劇。另外,摩擦熱效應還會顯著降低潤滑油膜的黏度,黏度的下降又會導致潤滑油膜的承載能力降低,甚至導致潤滑失效[5]。

研究表明：摩擦副表層或亞表層材料發(fā)生變形或撕裂時產生的能量大部分會轉化為熱能，引起摩擦表面溫度升高并向四周傳遞[6]。軸承摩擦過程中摩擦面作為生熱面，溫度會明顯高于外表面，傳統(tǒng)的測溫方法僅在軸承表面布置熱電偶測量單點溫度，對摩擦面及整體溫度場分布缺乏研究;又由于摩擦面和軸承內部的不可見性，其溫度值不宜直接獲得。因此有必要對軸承展開摩擦三維非定常溫度場的分析。

在平面滑動摩擦副的溫度場研究中,假設接觸區(qū)域壓力恒定，將理論計算與實測溫度對比可知,當考慮熱流率隨時間和旋轉半徑變化時，可以得到更符合實際的摩擦溫度場模型[7]。但關節(jié)軸承的摩擦副為空間球面,其接觸形式不同于赫茲接觸，需要進行數(shù)值方法求解[8]。又由于球面間隙的存在，因此假設球面完全協(xié)調接觸也會導致較大的計算誤差[9]。本文先使用有限元方法分析軸承接觸應力分布,結合實測摩擦力矩反求動態(tài)摩擦因數(shù)，根據(jù)摩擦生熱原理計算熱流率隨時間和空間坐標分布,并將其作為摩擦面的第二類邊界條件建立溫度場模型,然后使用熱像儀測試溫度進行試驗驗證,最后基于上述方法分別研究建模時忽略球面間隙和考慮球面間隙對軸承溫度場的影響。

1　試驗裝置與實體模型

如圖1所示，以GX25S推力型油潤滑關節(jié)軸承為試驗試樣,基于HDM-20型號端面磨損試驗機設計試驗夾具。試驗過程中,由下平臺的加載面施加向上的軸向載荷;試驗機通過銷槽傳遞扭矩,帶動芯軸和內圈做順時針單向旋轉運動;軸承外圈與下平臺采用過渡配合，裝置在下平臺的牽引螺釘連接拉力傳感器，可實時測量軸承摩擦力矩；試驗潤滑劑為鋰基潤滑脂。使用Thermo VisionTMA40-M在線紅外熱像儀拍攝軸承表面,獲得外表面實際溫度分布。

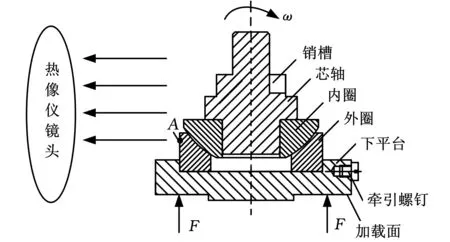
圖1　試驗原理圖

有限元建模時忽略芯軸的銷槽、潤滑油槽及其他細小特征的影響，則整體模型關于芯軸中心對稱,為縮短計算時間將其簡化為平面軸對稱模型。

由于試驗工況下軸承溫升較小,故假設材料各項參數(shù)在溫升范圍內未發(fā)生變化。各材料參數(shù)如表1所示。

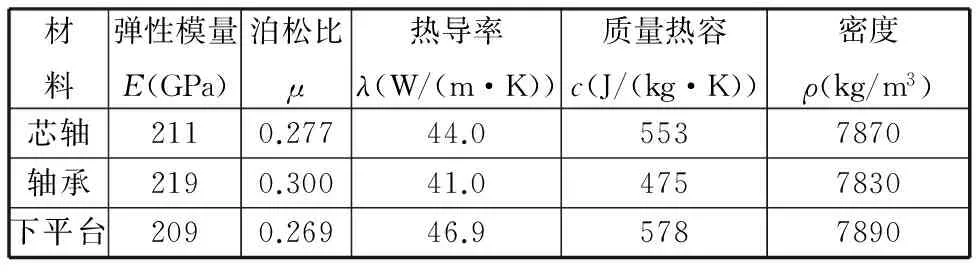
表1　材料屬性

2　有限元模型的建立

2.1模型建立及簡化

在軸承的實際結構中,為滿足儲存潤滑油及滿足轉動靈活的需要,外圈的球面直徑會略大于內圈的球面直徑。使用ZEISS三坐標儀分別測量內外球面直徑,實測值如下:外圈內徑為68.1000 mm,內圈外徑為67.9400 mm,兩球面的曲率半徑差值為0.008 mm。數(shù)據(jù)顯示,內外球面在幾何上存在初始的曲率半徑差值(下文中將這個差值統(tǒng)稱為球面間隙),而并非完全相同。但由于間隙值相對整體尺寸非常小,不利于有限元的建模處理，因此有研究在分析球面接觸應力時忽略了球面間隙的存在,假設內外球面完全一致,但試驗證明忽略間隙值會導致應力分析結果出現(xiàn)較大誤差[9]。為研究間隙值對接觸應力及溫度場的影響,分別將建模時忽略間隙(內外球面直徑均為68.000 mm)和考慮間隙(球面直徑為實測值)作為兩種不同情況進行有限元建模研究,則對球面接觸可作如下假設：①忽略間隙時球面完全接觸，假設內外球面接觸位置的溫度相同;②考慮間隙時,由于球面間隙極小并涂有大量潤滑脂，內外球面存在較大的熱交換，也假設內外圈球面接觸位置的溫度相同。

基于上述假設,在溫度場計算中使用MPC算法將接觸時對應球面位置的溫度自由度“系”在一起。

2.2摩擦熱量的計算

摩擦生熱量可由下式計算[10]:

q=μp vr

(1)

式中,q為單位接觸面積上產生的熱量,即熱流密度;μ為摩擦因數(shù);p為接觸正壓力;vr為接觸位置的相對線速度。

由式(1)可知,摩擦熱的生成與摩擦因數(shù)、接觸應力分布及相對線速度均有直接關系。

關節(jié)軸承試驗機上的摩擦因數(shù)計算式為[11]

(2)

式中,M為摩擦力矩;N為載荷;dk為球面直徑。

但式(1)并沒有考慮加載方式和球面間隙等參數(shù)對接觸應力及摩擦因數(shù)的影響,引入到熱流率的計算時會導致誤差較大。

采用等效離散法,在結構有限元中對模型進行網格劃分,可將球面等效成一系列不同半徑的圓環(huán)面接觸。假設在某一載荷條件下共有n個圓環(huán)參與實際接觸，忽略潤滑脂的影響，則各圓環(huán)對旋轉中心的摩擦力矩之和等于實測摩擦力矩。

試驗過程中,設各圓環(huán)摩擦因數(shù)為μi(t),則由力矩平衡可得

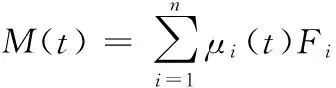
(3)

為簡化模型,假設各圓環(huán)摩擦因數(shù)相同,且均為μ(t),則有

(4)

式中,M(t)為實測摩擦力矩;Fi為圓環(huán)接觸總反力;ri為圓環(huán)半徑,且ri∈[17.25 mm,27.701 mm]。

根據(jù)式(1),摩擦生熱量可表示為

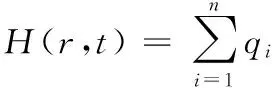
(5)

式中,H(r,t)為熱流率;ω(t)為旋轉角速度;Ai為圓環(huán)面積。

對任一圓環(huán)有

Fi=piAi

(6)

因此,關節(jié)軸承的球面摩擦熱流率可表示為

Hi(r,t)=μ(t)Fiω(t)ri

(7)

2.3熱量傳導及定解條件

基于傅里葉導熱定律,對各向同性的固體導熱有如下方程[12]：

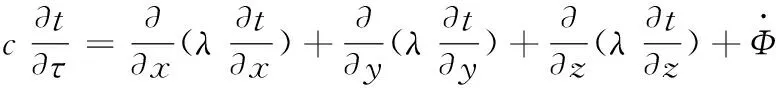
(8)

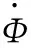
定解條件包括初始條件和邊界條件。試驗在室溫下進行，初始溫度為25 ℃。

對流換熱可根據(jù)牛頓冷卻公式計算：

Φ=hA(Tw-Tf)

(9)

式中,h為表面換熱系數(shù);A為表面面積;Tw和Tf分別為表面溫度和環(huán)境溫度。

熱輻射計算為非線性,增大了收斂難度,因此將傳熱系數(shù)提高10%替代熱輻射效果[13]。

2.4有限元計算

根據(jù)式(7)所需參數(shù),使用APDL語言編寫計算控制程序，程序流程如圖2所示。

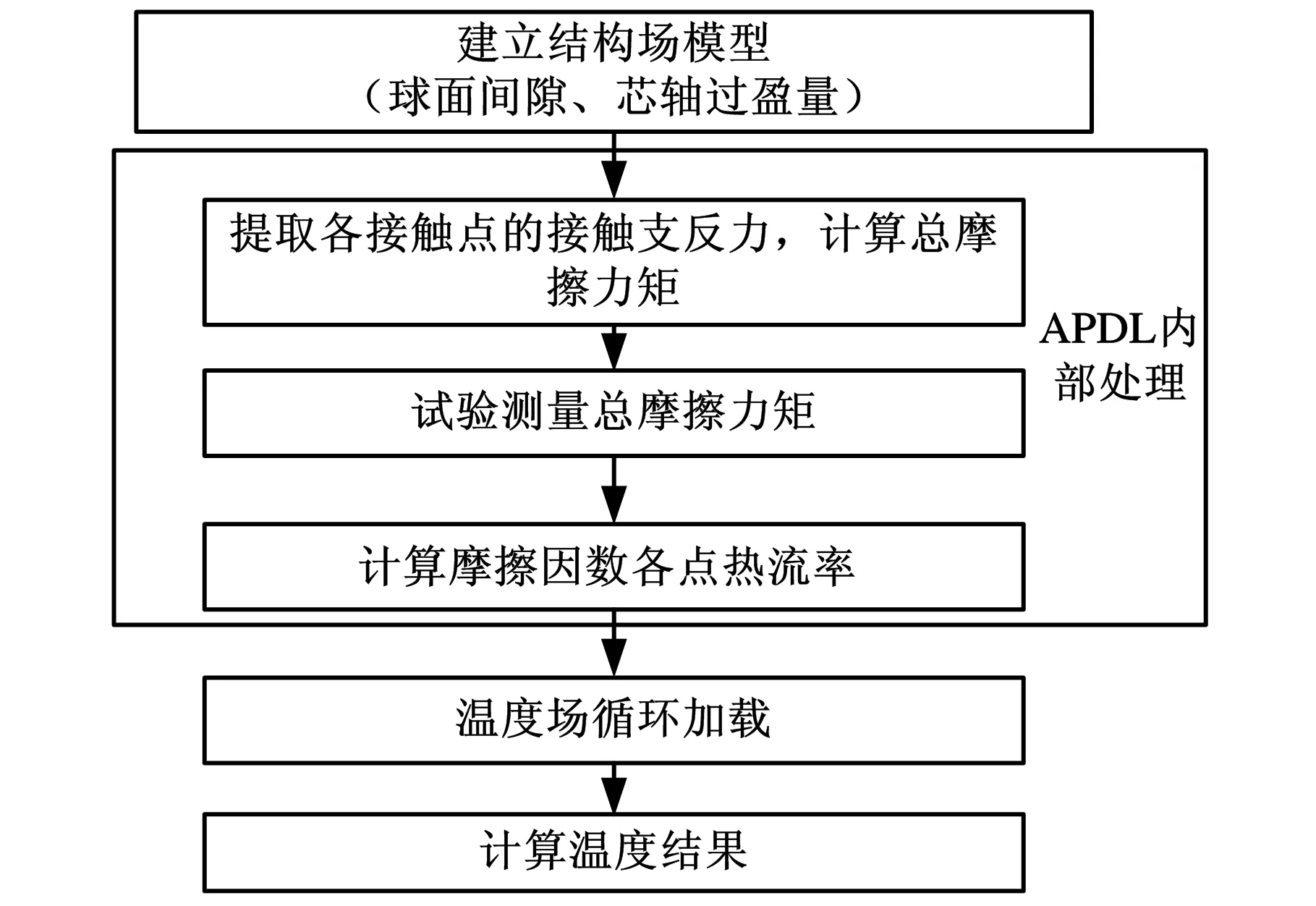
圖2　APDL程序流程圖

試驗工況為：載荷2 kN,轉速30 r/min。按照圖2所示流程,程序先計算出兩類模型下的接觸應力分布(圖3),再根據(jù)實測摩擦力矩計算出實時摩擦因數(shù)(圖4),結合接觸反力、摩擦因數(shù)及轉速計算出熱流率分布(圖5),最后計算出溫度場(圖6)。

3　結果與分析

3.1接觸應力分布

圖3所示分別為兩類模型的球面接觸應力徑向坐標的變化情況。其中無間隙模型是假設內外球面直徑均為68.000 mm,軸承內外圈恰好處于完全協(xié)調接觸；有間隙模型根據(jù)實測球面的曲率半徑進行建模處理，軸承內外圈在初始狀態(tài)下并未接觸，由于載荷的施加，初始間隙被逐漸合并，并最先在球面底部產生初始接觸。

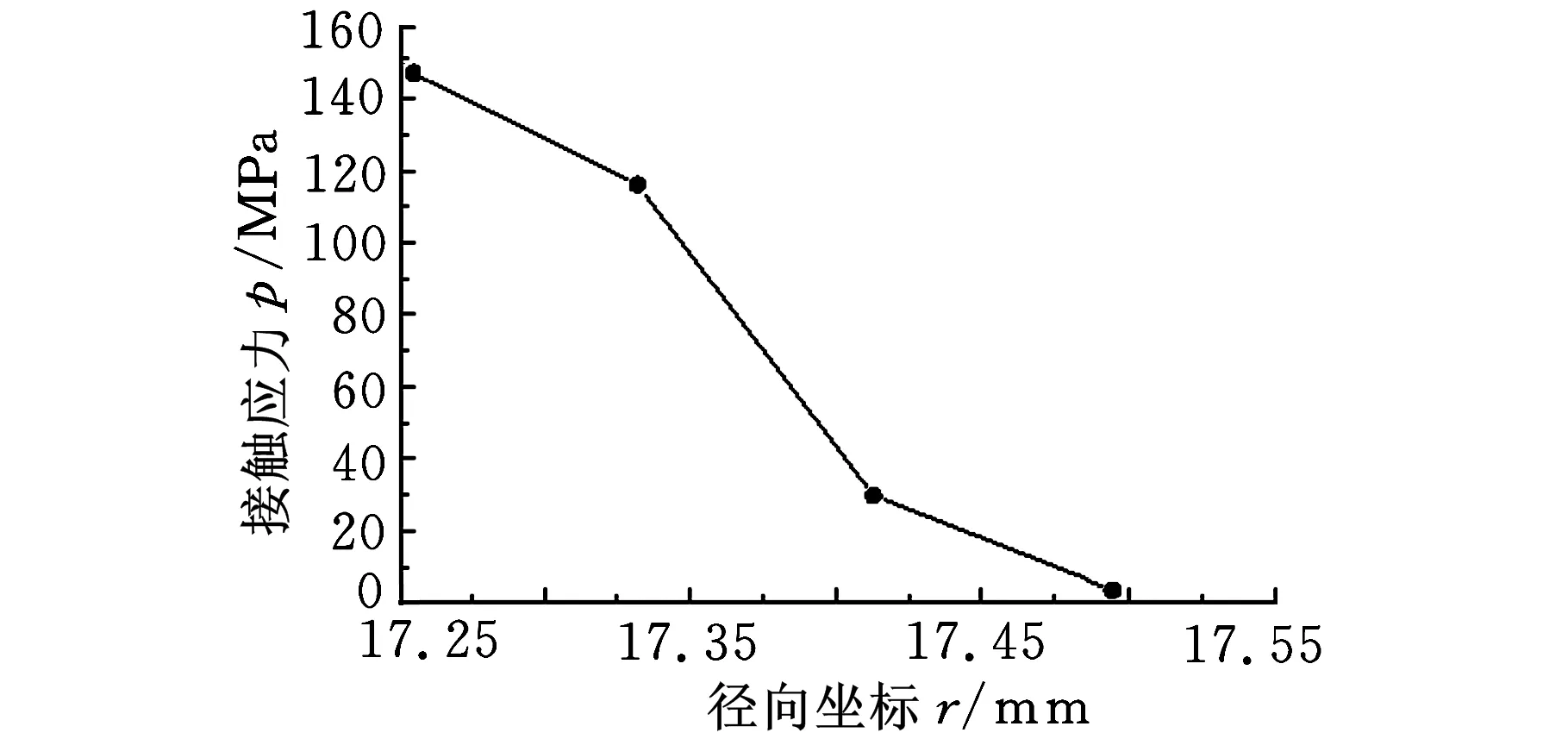
(a)軸承內外圈有間隙

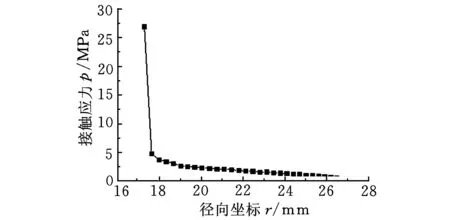
(b)忽略軸承內外圈間隙圖3　接觸應力

由圖3可知:兩類模型均在球面最底端出現(xiàn)最大接觸應力，且均隨徑向坐標的增大先急劇減小，而后下降趨勢趨于平緩。無間隙模型與文獻[9]得到了類似的接觸應力分布趨勢，間隙模型接觸區(qū)域的徑向坐標范圍遠遠小于無間隙情況，其最大接觸應力也遠遠大于無間隙狀態(tài)。這是因為間隙模型中球面間隙破壞了球面接觸的協(xié)調性，初始接觸時只有球面最底端的區(qū)域參與接觸，導致其應力分布與無間隙模型出現(xiàn)明顯差異。此外，由式(1)可知，接觸應力的分布會直接影響摩擦生熱量在空間上的分布;由式(4)可知,接觸應力的分布也同時影響摩擦因數(shù)的反推。因此建模時考慮實際的幾何間隙,可以提高熱流率的計算精度。

3.2摩擦因數(shù)及熱流率

圖4中,在忽略間隙和計入間隙兩種模型中,摩擦因數(shù)與摩擦力矩的變化趨勢均保持一致,但無間隙模型反推出的摩擦因數(shù)明顯小于有間隙模型反推出的摩擦因數(shù)。由于二者采用相同計算方法由相同摩擦力矩反推得到,無間隙模型中球面接觸區(qū)域較大，軸承轉動不靈活易造成較大摩擦力矩，因此反推出的摩擦因數(shù)較有間隙模型反推出的摩擦因數(shù)偏小。

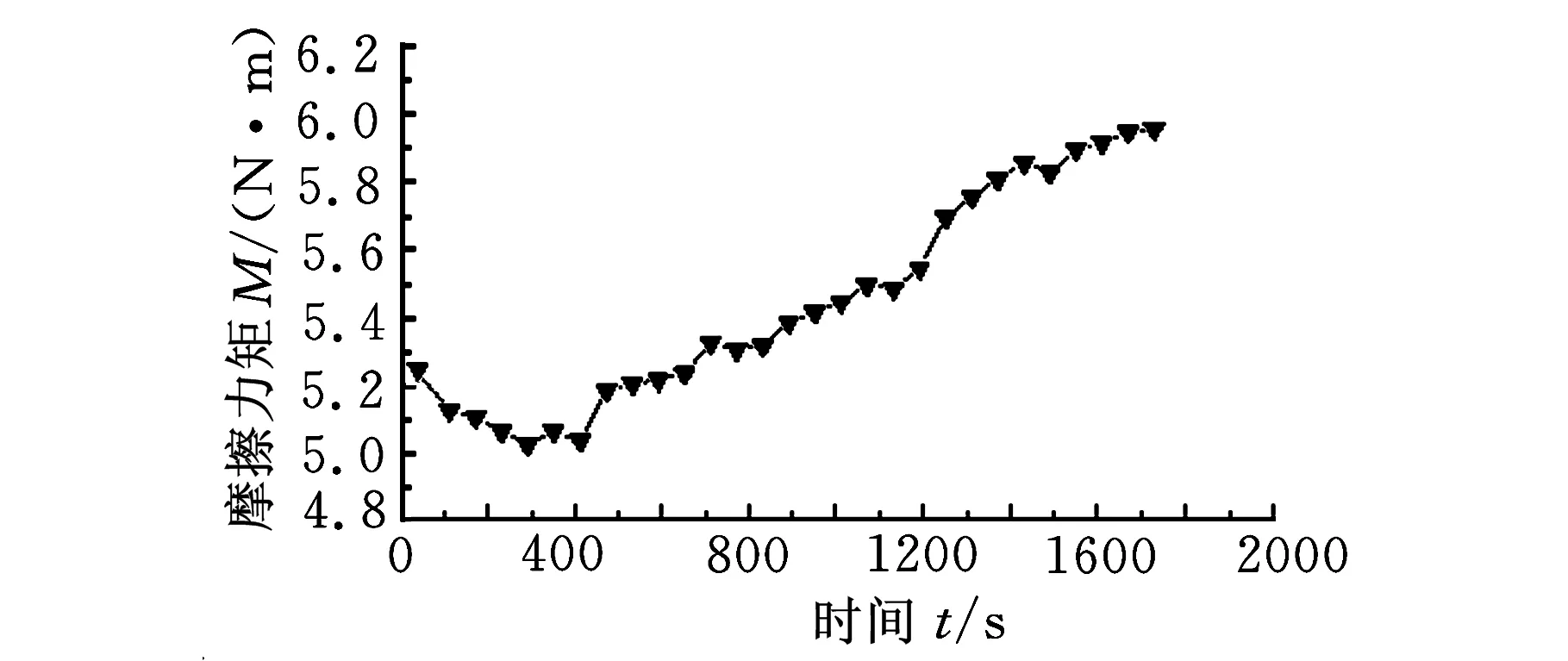
(a)摩擦力矩

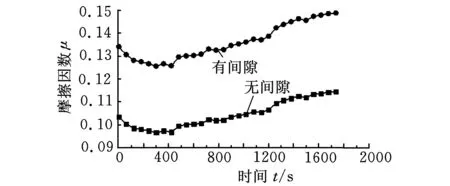
(b)摩擦因數(shù)圖4　摩擦力矩及摩擦因數(shù)

圖5中兩類模型的熱流率均隨球面徑向坐標和時間變化。有間隙模型中接觸面上只有球面最底端附近區(qū)域有摩擦熱生成，無間隙模型的熱流率分布范圍比有間隙模型的熱流率分布范圍更廣,但其峰值也明顯偏小。根據(jù)式(1)可知，在相同的轉速下接觸應力分布和摩擦因數(shù)直接決定摩擦熱的分布,因此兩類模型的熱流率在空間上分布與接觸應力分布成正比，在時間上的變化與動態(tài)摩擦因數(shù)的變化成正比。

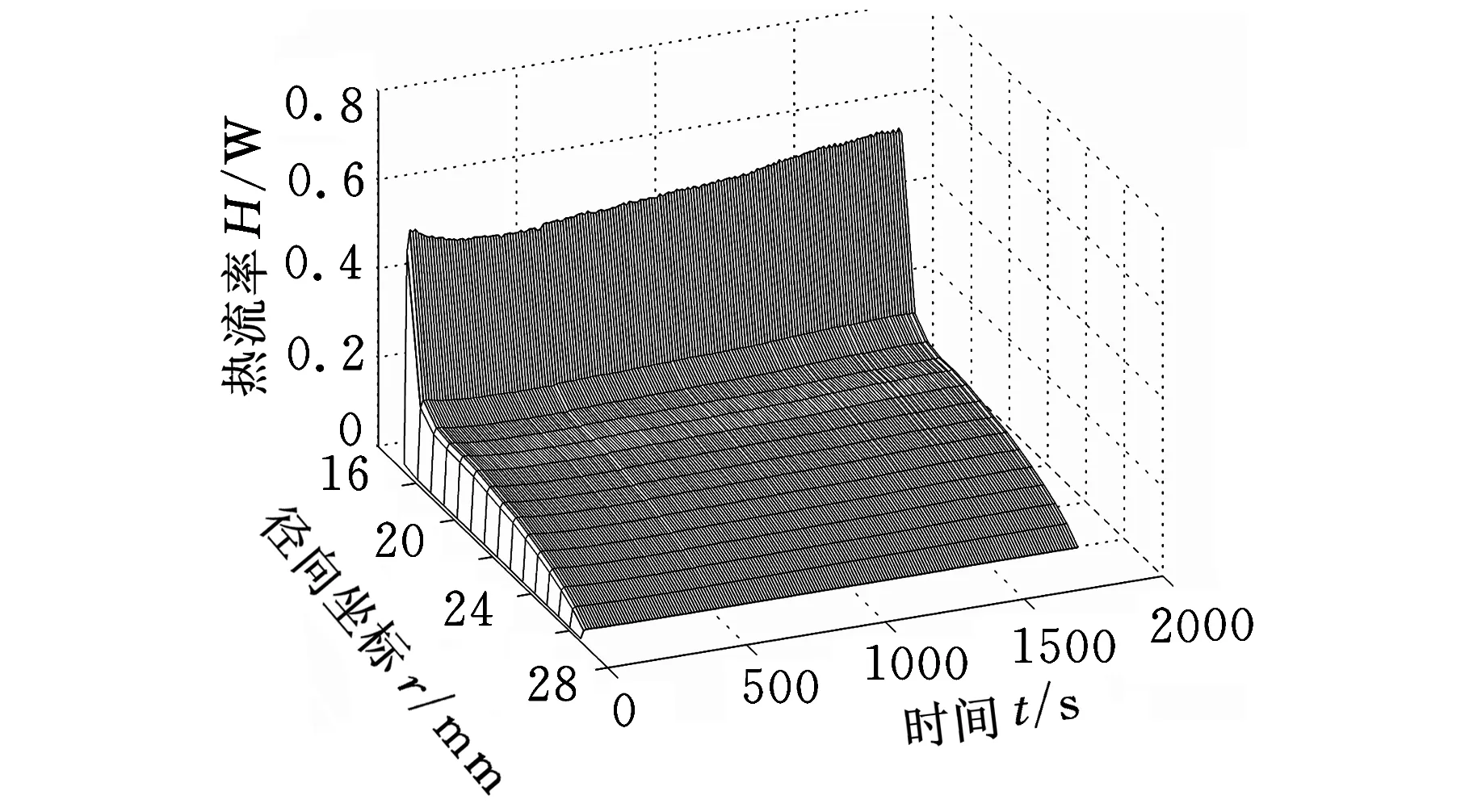
(a)無間隙狀態(tài)下熱流率分布

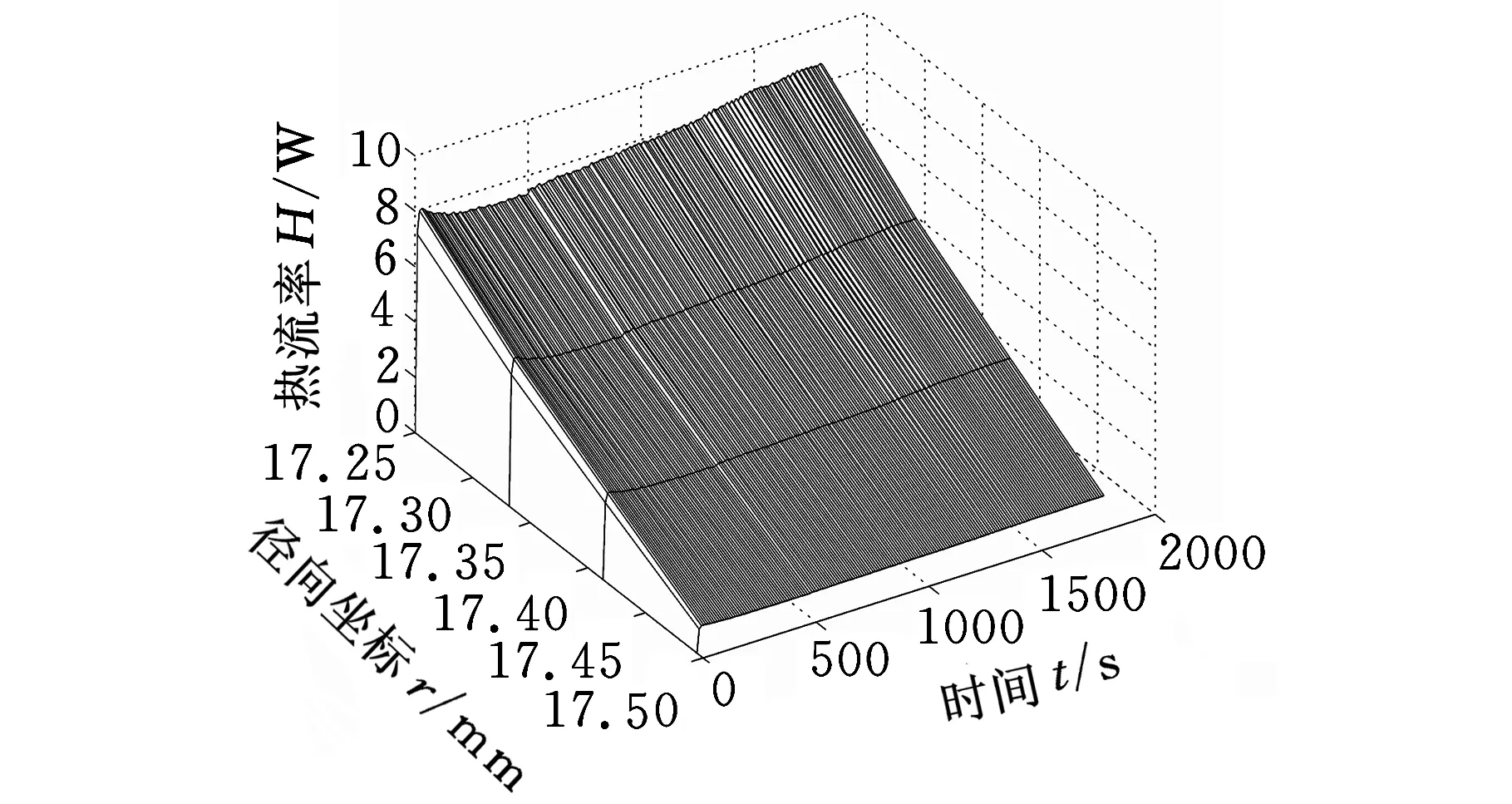
(b)間隙狀態(tài)下熱流率分布圖5　熱流率分布

3.3溫度分布及驗證

圖6為軸承外圈在1800 s時的溫度灰度圖。由圖6可知:兩類模型的總體溫升大致相同，最高溫度都出現(xiàn)在球面底部；但二者的溫度場分布出現(xiàn)較大差異，無間隙模型的總體溫度分布更加均勻，摩擦生熱區(qū)域與軸承表面的溫差較間隙模型更小。出現(xiàn)此類現(xiàn)象的原因主要為：①式(7)是將摩擦阻力做功轉換成熱能，因此單位時間內輸入軸承的總熱量相同，在相同的散熱邊界條件下,兩類模型的總體溫升也大致相同；②圖6中兩類模型的熱流率都集中于球面底部，故大量熱量輸入此處形成高溫區(qū)；③無間隙模型的接觸區(qū)域大于間隙模型，有利于球面上生成的摩擦熱向低溫區(qū)擴散并形成較均勻的溫度分布，而間隙模型的生熱區(qū)域明顯偏小，不利于溫度擴散，因此摩擦面的最高溫度與軸承表面出現(xiàn)更大的溫差。

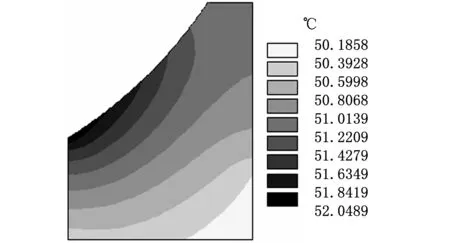
(a)無間隙模型

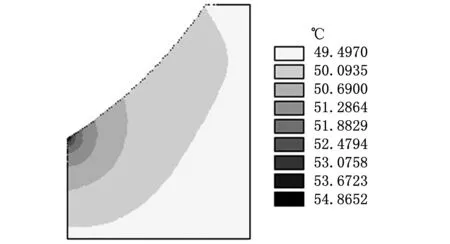
(b)有間隙模型圖6　軸承外圈溫度分布

取軸承外圈表面距上表面3 mm處點A(圖1所示)作為溫度驗證點，實測溫度與計算溫度隨時間變化曲線如圖7所示。

在摩擦前期,理論計算值與測量值都以較快速度上升并基本保持一致；隨著時間的延長溫升速度均有所減緩，無間隙模型溫度逐漸高于間隙模型溫度和實測溫度，實測溫度低于兩類模型的計算溫度且差距逐漸增大。在第30 min計算值與實測值出現(xiàn)最大誤差，實測值與無間隙模型的誤差約為6.75℃,實測值與間隙模型的誤差約為4.53℃。

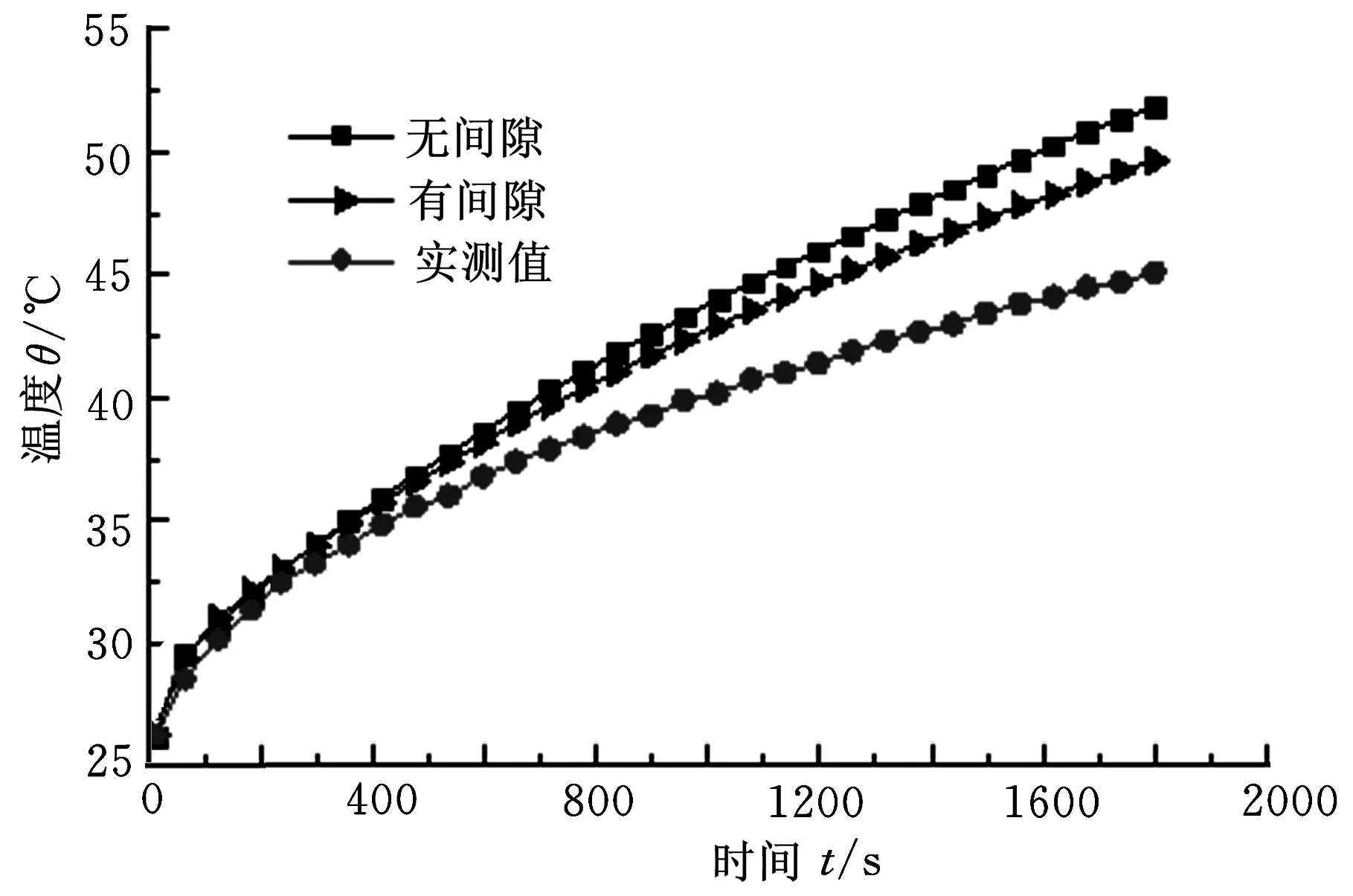
圖7　驗證點溫升過程對比

分析產生誤差的原因為:①建模過程中將幾何模型的細小特征作了簡化,同時也忽略了潤滑油和磨屑帶走的熱量，導致計算溫度偏高；②有研究指出金屬摩擦生熱過程中摩擦力所做功約有95%轉化為熱量[14],而式(7)假設摩擦力做功全部轉化為熱能也會造成理論計算溫度高于實測溫度;③無間隙模型的熱量流入范圍較大，熱源距離測溫點的距離也較間隙模型更近,導致A點溫升高于間隙模型的溫升，同時誤差也大于間隙模型的誤差。另外，由于球面間隙較小，高溫導致的熱變形會改變球面的接觸面積，進而影響熱流率在空間上的分配，當使用溫度較高時需要進一步考慮熱力耦合的影響。

4　結論

(1)球面間隙的存在對球面接觸應力分布、摩擦因數(shù)及摩擦熱的生成均有重要影響，建模時忽略間隙值會產生較大誤差。

(2)摩擦產生的熱流率隨時間和空間坐標動態(tài)變化,其中動態(tài)的摩擦因數(shù)決定熱流率在時間上的變化規(guī)律，接觸應力分布決定熱流率在空間上的能量分配。

(3)根據(jù)間隙模型的分析結果，當軸承使用溫度在50 ℃左右時，內部高溫區(qū)比軸承表面溫度高出約5℃，因此，在試驗中通過測量表面溫度判斷軸承實際溫升的方法存在較大誤差。

(4)依據(jù)本文建立的間隙模型,在已知軸承尺寸、材料參數(shù)及換熱條件的情況下，結合試驗所得摩擦力矩可以反推實時摩擦因數(shù)和熱流率分布。

[1]Kim B C,Park D C,Kim H S,et al.Development of Composite Spherical Bearing[J].Composite Structures,2006,75(1):231-240.

[2]潘漢明,陳以一,趙憲忠,等.廣州新電視塔雙向鉸節(jié)點試驗研究[J].工業(yè)建筑,2009(1):117-121.

Pan Hanming,Chen Yiyi,Zhao Xianzhong,et al.Experimental Study on Bidirectional Pin-hinged Joints of Guangzhou New TV Tower[J].Industrial Construction,2009(1):117-121.

[3]Germaneau A,Peyruseigt F,Mistou S,et al.3D Mechanical Analysis of Aeronautical Plain Bearings:Validation of a Finite Element Model from Measurement of Displacement Fields by Digital Volume Correlation and Optical Scanning Tomography[J].Optics and Lasers in Engineering，2010,48(6):676-683.

[4]《機械工程材料性能數(shù)據(jù)手冊》編委會.機械工程材料性能數(shù)據(jù)手冊[M].北京:機械工業(yè)出版社,1995．

[5]溫詩鑄, 黃平. 摩擦學原理[M].北京：清華大學出版社有限公司, 2002.

[6]Yang Jianheng.Analysis to the Thermal Mechanism of Wear in Dry Friction Condition[J].Lubrication Engineering,2005,171(5):173-176.

[7]魏巍,俞建衛(wèi),沈持正,等.基于試驗數(shù)據(jù)的滑動摩擦溫度場仿真方法研究[J].中國機械工程,2013,24(18):2426-2430.

Wei Wei,Yu Jianwei,Shen Chizheng,et al.Research on Sliding Friction Temperature Field Simulation Method Based on Experimental Data[J].China Mechanical Engineering,2013,24(18):2426-2430.

[8]Germaneau A,Peyruseigt F,Mistou S,et al.Verification of a Spherical Plain Bearing Finite-element Model Using Scattered Light Photoelasticity Tests[J].Proceedings of the Institution of Mechanical Engineers,Part J:Journal of Engineering Tribology,2008,222(5):647-656.

[9]劉六井,高偉.大型推力關節(jié)軸承結構有限元分析[J].船海工程,2004(2):25-27.

Liu Liujing,Gao Wei.The Structure Finite Element Analysis of Large-scale Thrust Jiont Bearing[J].Ship and Ocean Engineering,2004(2):25-27.

[10]Yang Y C,Chen W L.A Nonlinear Inverse Problem in Estimating the Heat Flux of the Disc in a Disc Brake System[J].Applied Thermal Engineering,2011,31(14):2439-2448.

[11]王國鋒. 復合擺動式關節(jié)軸承性能試驗機的研制及試驗研究[D].洛陽:河南科技大學, 2011.

[12]楊世銘,陶文銓.傳熱學[M].3版.北京:高等教育出版社, 1998.

[13]李奇亮. 基于界面測溫的面接觸摩擦溫度場研究[D].合肥:合肥工業(yè)大學,2009.

[14]Majcherczak D,Dufrenoy P,Berthier Y.Tribological Thermal and Mechanical Coupling Aspects of the Dry Sliding Contact[J].Tribology International,2007,40:834-843.

(編輯王艷麗)

Calculation Method of Spherical Plain Bearing Friction Temperature Field

Yu JianweiWang LifeiWei Wei

Hefei University of Technology,Hefei,230009

Taking thrust spherical plain bearing as the research object,the contact stress under axial load was analyzed and based on the experimental friction torque the dynamic friction coefficient was solved.Then combined with contact stress and friction coefficient,heat flow rate was calculated and served as the second boundary condition for the unsteady temperature field finite element analysis of the bearing.Finally,using infrared camera to shoot the outer surface of two-dimensional temperature distribution of the bearing friction process,then reliability of simulation results was tested.Simulation and experimental results show that: the calculation method has solved the problems of accurate calculation of spherical friction coefficient and spatial distribution of the heat flow rate.Ignoring the spherical gap when modeling will affect the contact stress distribution directly and cause a larger error in temperature distribution.Considering a spherical gap a more accurate bearing friction temperature field can be obtained.

spherical plain bearing;spherical gap;contact stress;temperature field;infrared measurement;finite element

2014-06-13

國家自然科學基金資助項目(51075114)

TH117.1DOI：10.3969/j.issn.1004-132X.2015.10.002

俞建衛(wèi),男,1956年生。合肥工業(yè)大學摩擦學研究所及安徽省粉末冶金工程技術研究中心研究員。主要研究方向為摩擦學測試技術。王禮飛,男,1991年生。合肥工業(yè)大學機械與汽車工程學院碩士研究生。魏巍，男，1986年生。合肥工業(yè)大學儀器科學與光電工程學院博士研究生。