基于過控制頂點曲線的微線段過渡插補方法

吳　婷　張禮兵　黃風立

嘉興學院,嘉興,314001

基于過控制頂點曲線的微線段過渡插補方法

吳婷張禮兵黃風立

嘉興學院,嘉興,314001

針對微線段數控加工過程中的插補問題,為減小微線段數控加工中的速度波動,實現轉接點的平滑過渡,提出過控制頂點曲線的過渡插補算法。首先構建微線段曲線的過渡矢量模型,根據基于特征多邊形頂點的曲線模型的幾何特性,構建過控制頂點曲線的過渡矢量模型,然后采用過控制頂點曲線過渡模型對微線段進行插補計算,根據加工誤差計算控制頂點,確定約束速度并實時進行前瞻處理,最后通過實例進行了驗證。實驗結果表明,所提出的方法有效地提高了微線段轉接速度,縮短了加工時間，實現了曲線的平滑過渡。

數控加工;微線段插補;曲線過渡;前瞻控制;過控制頂點曲線

0　引言

隨著計算機和先進制造技術的發展，高速高精度加工已成為現代數控技術一個重要的發展方向。數控加工代碼通常由CAM系統生成大量的微線段,這些微線段具有數量大、長度短等特點[1],其中長度為毫米級,有的甚至為亞微米級,而且生成的數控加工程序沒有考慮相鄰微線段之間轉接點對加工精度、加工速度和加工質量的影響[2],如果直接按照數控代碼進行加工必然引起伺服電機啟動頻繁,對數控機床產生較大的沖擊,從而縮短刀具使用壽命,同時也耗費更多的加工時間,影響數控加工精度和加工效率[3],因此,對微線段數控加工進行平滑插補處理是提高加工精度和加工效率的一種有效方法。

針對微線段平滑加工研究方法主要有:直接過渡法、局部過渡法和曲線擬合法。王宇晗等[4]根據相鄰小線段間約束條件建立了小線段高速加工速度銜接模型。Ye等[5]提出了一種基于前瞻算法的連續小線段插補方法,這種方法可提高系統運動的平穩性。張立先等[6]采用多個插補周期進行拐角過渡以提高線段連接處的轉接速度。這些方法均采用直接過渡法對微線段進行平滑處理。通過分析，直接過渡法主要存在以下問題:①不能保證連接點處單個軸的加速度小于或等于系統允許的加速度，當某個軸的速度波動較大時，會對機床產生較大的沖擊；②線段間實際連接點并不一定與理論連接點重合,從而存在轉接誤差，當轉接誤差較大時，影響轉接點處的加工精度。一些研究人員采用局部過渡法對微線段進行過渡處理,如何均等[7]采用圓弧對相鄰微線段進行過渡處理以提高過渡速度，另外，何均等[8]也提出基于Ferguson樣條曲線的微線段過渡算法以實現數控加工的平穩過渡。與直接過渡法相比，局部過渡法更有利于實現速度的平滑過渡。Li等[9]采用五次樣條曲線對微線段進行擬合,Wang等[10]和沈斌等[11]采用NURBS曲線對微線段進行擬合。Yau等[12]提出了基于Bezier曲線過渡方法。任錕等[13]對離散加工路徑采用五次樣條曲線擬合分析,預估高曲率點處最優速度，實現了加工速度的平滑過渡。采用曲線擬合方法對微線段進行插補處理,由于擬合過程計算量大，運算復雜，所以難以滿足數控系統的實時性要求。綜上所述，局部過渡法更有利于實現微線段之間的平滑過渡。但是目前局部過渡方法所采用的曲線并不通過控制頂點，控制頂點的位置僅僅控制曲線的基本形狀，而不能直接控制曲線的變化，不能有效保證曲線的幾何精度。因此，研究過控制頂點的光滑曲線過渡插補方法，有利于保證過渡曲線的形狀和幾何精度，從而有效提高微線段加工精度和效率。

1　曲線過渡矢量模型

為實現連續微線段高速平滑加工,在相鄰微線段之間插入一段曲線,曲線過渡矢量模型如圖1所示,P0P1和P1P2分別為相鄰的兩條微線段,S(u)為插入的過渡曲線,G0和G2點分別為曲線S(u)與微線段P0P1和P1P2的切點,G1點為∠P0P1P2的平分線與過渡曲線S(u)的交點。在保證加工精度的條件下，微線段P0P1和P1P2加工軌跡由線段P0G0、曲線S(u)和線段G2P2所代替,從而實現微線段高速加工的平滑過渡。為了確保插入曲線實現平滑過渡,ΔG0P1G2為等腰三角形,曲線段G0G1和G1G2關于∠P0P1P2的平分線P1G1軸對稱。

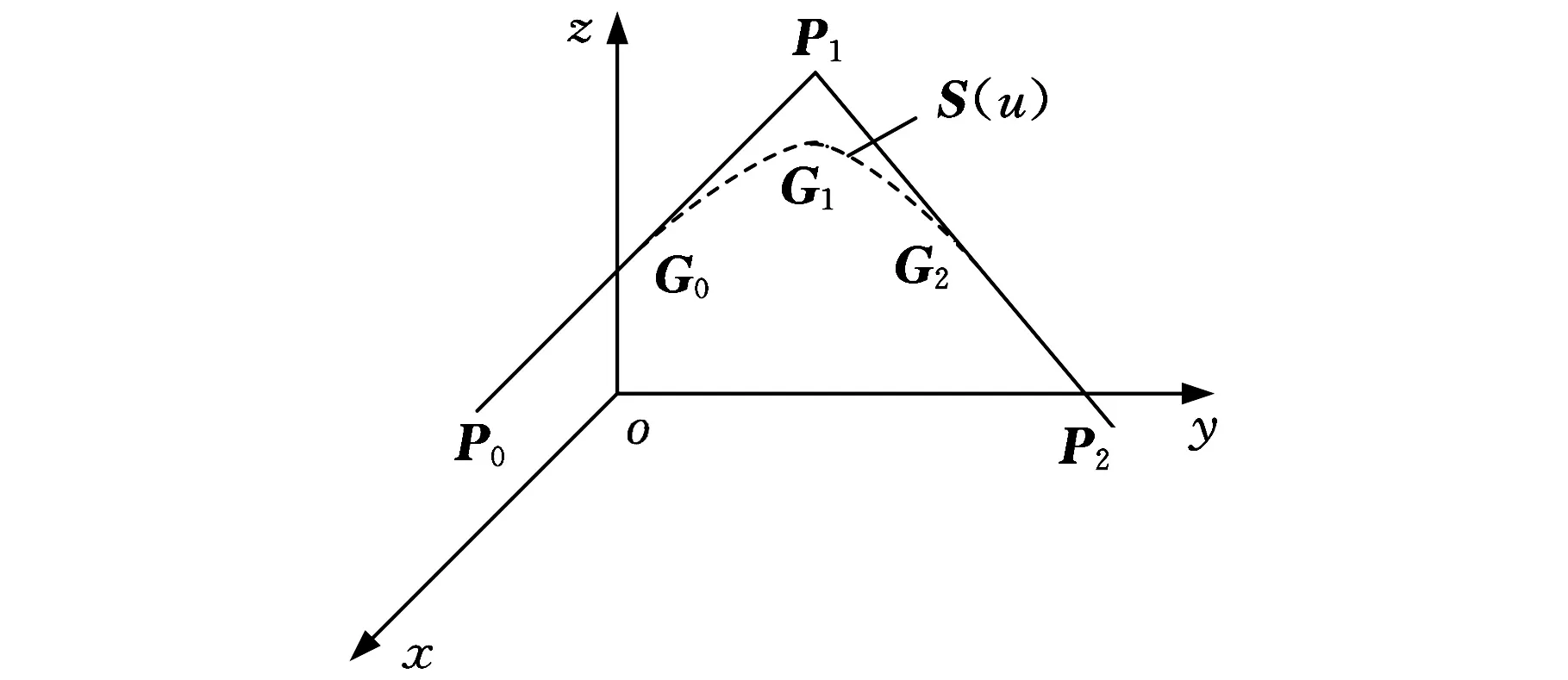
圖1　微線段數控高速加工曲線過渡矢量模型

1.1基于特征多邊形頂點的曲線模型

在連續微線段數控加工過程中,相鄰微線段之間采用過控制頂點的二次曲線進行局部過渡，通過曲線的幾何特性確保系統的精度要求,相對于三次或者更高次曲線而言，二次曲線計算量較小，過渡處理所耗費的時間短，從而滿足數控系統的精度和實時性要求。

基于特征多邊形頂點的二次曲線表達式以矢量形式表示為

(1)

式中,Si(u)為二次曲線;Di、Di+1和Di+2為二次曲線的特征多邊形頂點;u為參數,u∈[0,1]。

基于特征多邊形頂點的二次曲線,首末兩端點的位置分別表示為

(2)

式中,Si(0)為二次曲線首端位置;Si(1)為二次曲線末端位置。

對式(1)求導，得到

(3)

基于特征多邊形頂點二次曲線,首末兩端點的切矢分別表示為

(4)

根據式(2)和式(4),得到該曲線的幾何特性如下：①首末兩端點通過特征多邊形相應邊的中點；②首末兩端點的切矢方向與特征多邊形的相應邊重合。

1.2過控制頂點曲線過渡模型

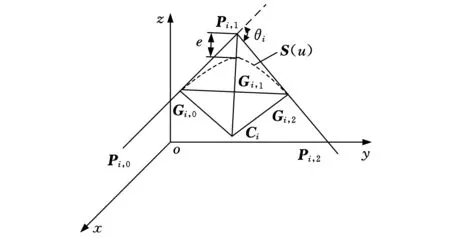
圖2過控制頂點的二次曲線過渡模型

過控制頂點的曲線過渡模型如圖2所示,點Pi,1為線段Pi,0Pi,1和Pi,1Pi,2的拐點,θi為相鄰兩線段之間的夾角,曲線Gi,0Gi,2為過渡曲線,Gi,0和Gi,2點均為微線段與過渡曲線之間的轉接點,拐點Pi,1到轉接點Gi,0和Gi,2的距離稱為過渡距離。曲線Gi,0Gi,1和Gi,1Gi,2關于直線Pi,1Gi,1對稱,點Gi,1為過渡曲線的中點,e為過渡曲線與微線段之間的偏差。

如圖2所示,已知曲線首末兩端點分別為Gi,0和Gi,2,確定曲線特征多邊形頂點Di,0、Di,1和Di,2基于特征多邊形頂點二次曲線的幾何特性①,可得

(5)

根據式(4)可得

(6)

(7)

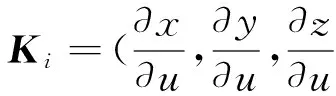
(8)

聯立式(5)～式(7),可得到二次曲線的特征多邊形頂點與控制頂點之間的關系表達式，用矢量形式可表示為

(9)

根據式(1)和式(9),可得過已知控制頂點二次曲線的數學模型表達式為

(10)

2　曲線過渡插補算法

在進行微線段數控加工高平穩控制時,需要控制曲線過渡的加工誤差。因此，在曲線過渡插補算法實現過程中，需要考慮三個問題:①根據微線段的幾何特征和加工精度要求，計算曲線過控制頂點的位置；②根據特征多邊形頂點二次曲線的幾何特征、動力學分析和極限速度等條件，確定數控加工過渡曲線的速度約束；③實時前瞻處理，實時構造過渡曲線和確定微線段的減速點，滿足系統實時性要求。

2.1控制頂點的計算

由于Gi,1為過渡曲線的中點(圖2),由式(10)可得

(11)

當采用過控制頂點二次曲線對微線段進行平滑過渡時,實際加工路徑與原始加工路徑之間會產生一定的偏差,為確保零件加工精度,需要對偏差量進行有效控制。假設系統允許的最大加工誤差為emax,根據加工誤差得到相鄰微線段的過渡長度為li,線段Pi,0Pi,1和Pi,1Pi,2的長度分別為Li,0和Li,1,求得過渡曲線的起點Gi,0和終點Gi,2位置坐標,以矢量形式表示為

就在族長即將暴怒時，一個聲音從后方天葬院中傳了出來：“我以天葬師之名，接受你的訴求，為了云浮的未來，敬祈天神！”

(12)

線段Gi,0Gi,2的中點坐標矢量滿足與(Gi,0+Gi,0)/2相等，根據拐點Pi,1、弦長中點和Oi點之間的關系,求得Oi的位置坐標滿足以矢量形式表示為

(13)

點Gi,1將線段OiPi,1分成兩段,可求得點Gi,1的位置坐標,以矢量形式表示為

(14)

根據式(11)～式(14),得到的li為變量的方程是一個無理二次方程,需要進行迭代求解,計算量較大,難以滿足數控系統的實時性要求,因此,在獲取加工誤差與微線段的過渡長度li之間的關系時,為滿足系統實時性要求,進行簡化求解,提出一種假設圓弧過渡方法。

如圖3所示,假設過渡曲線采用圓弧過渡,實際加工路徑與原始加工路徑的偏差為δi,可得到δi與emax之間的關系為

δi=αemax

通過RtΔGi,0Pi,1Ci得到微線段的過渡長度與數控系統所允許的最大偏差之間的關系如下：

(15)

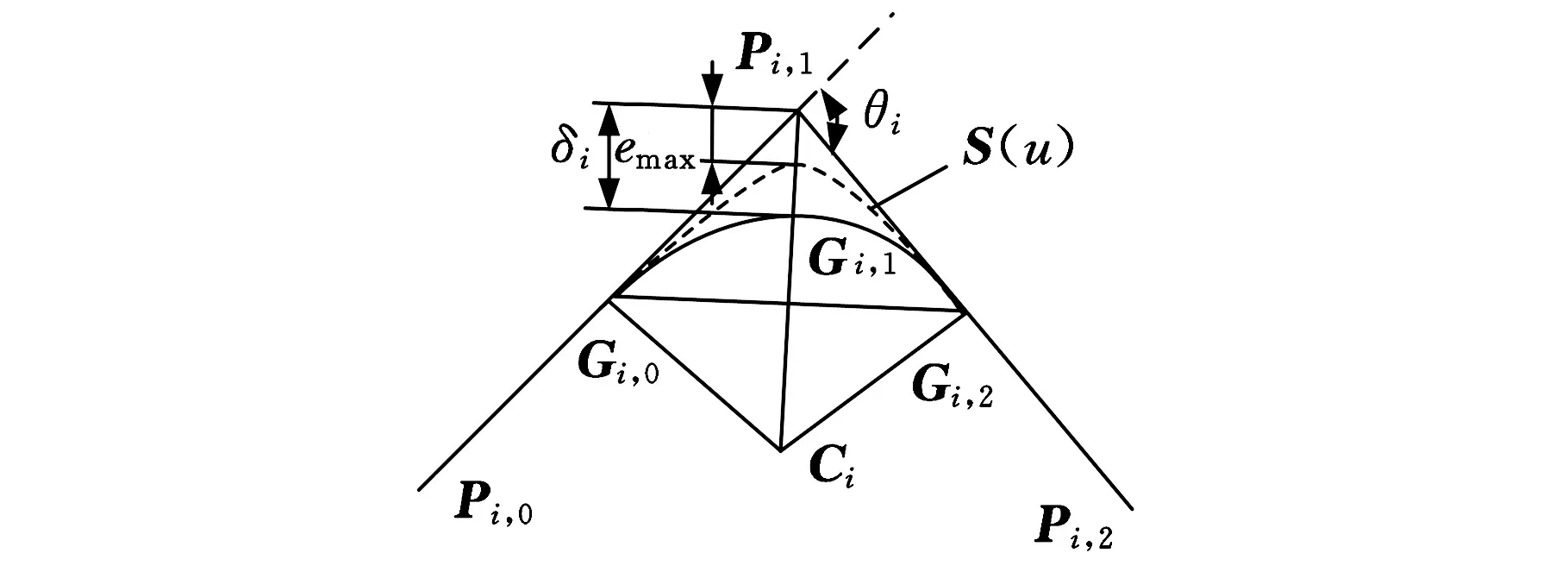
圖3　微線段假設圓弧過渡模型

根據式(12)和式(15),可得到曲線的控制頂點Gi,0和Gi,2位置,用矢量形式表示為

(16)

2.2約束速度的確定

當采用過渡曲線進行插補時,產生的弦高誤差與過渡曲線曲率半徑和進給速度之間存在耦合關系。為使產生的弦高誤差在系統允許范圍內,根據過渡曲線的幾何特性對進給速度加以限制。如圖4所示，設數控系統最大弦高誤差為δmax,進給速度為vi,插補周期為T,過渡曲線曲率變徑為Ri,則弦長為過渡曲線的插補長度。根據曲線的幾何關系得到弦高誤差、進給速度和曲率半徑之間滿足下列關系：

(17)

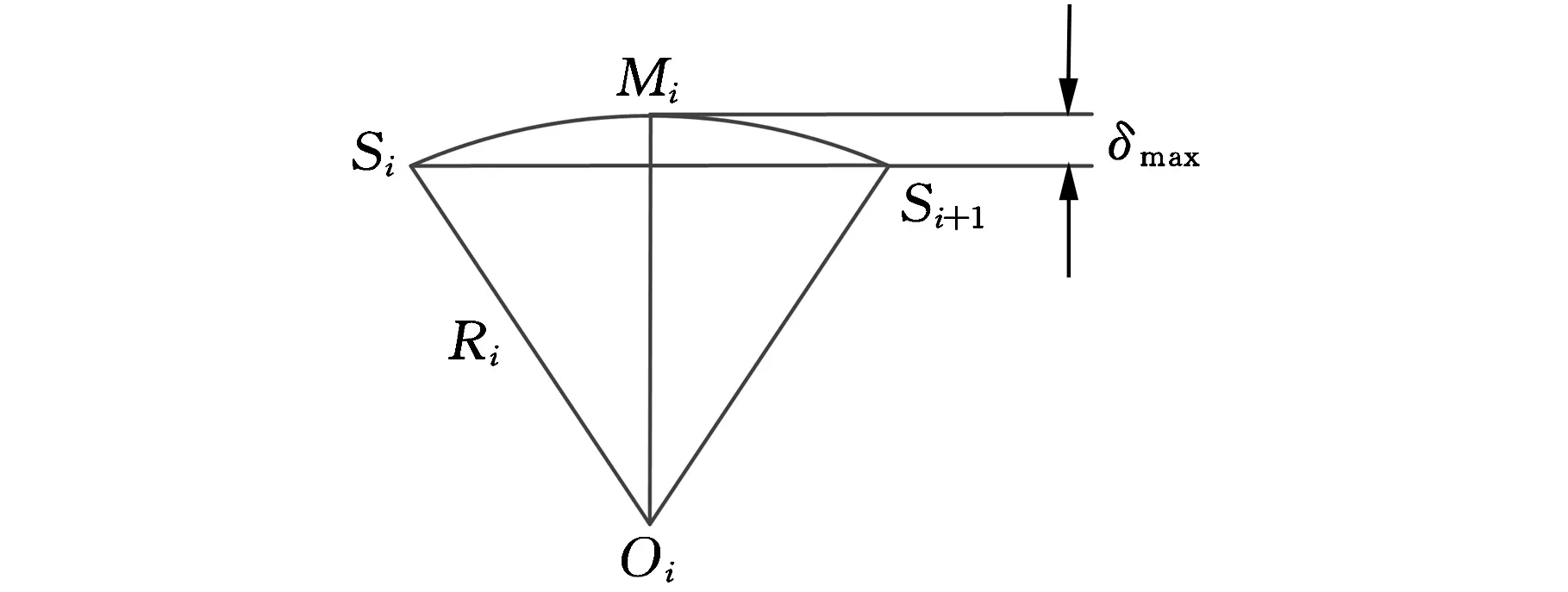
圖4　弦高誤差與進給速度關系圖

在實際加工過程中,為了減少機床的振動,需要考慮機床動力學特性,系統最大允許加速度為amax,由系統最大加速度對加工速度的限制,得到進給速度與加速度之間關系為

(18)

為實現過渡曲線高平穩和高精度加工,加工速度既要滿足弦高誤差和機床機械特性的限制,又要考慮數控系統所允許的最大進給速度vmax,因此綜合考慮三個方面,得到過渡曲線的速度約束條件為

(19)

2.3實時前瞻處理

當連續微線段數控加工采用過控制頂點曲線進行過渡時,加工路徑由一系列的微線段和過控制頂點的過渡曲線組成。為了滿足數控系統的實時性要求，采用滾動式前瞻控制技術對過渡曲線進行前瞻處理。滾動式前瞻控制技術在對當前微線段進行插補計算的同時，還要向前預讀多段微線段進行前瞻處理，隨著插補的進行，前瞻處理依次向前滾動，從而保證數控加工的前瞻性和連續性。前瞻處理包括兩個部分：一是構造過控制頂點的曲線；二是確定預處理微線段的約束速度和減速點。

(1)構造過控制頂點的曲線。通過實時前瞻處理預先獲取待加工微線段的幾何信息,提前對相鄰微線段進行曲線過渡,其實現過程如下:①根據系統允許的最大偏差，計算微線段的過渡長度;②根據式(16)確定曲線的控制頂點；③根據前瞻處理的相鄰微線段，計算微線段的直線方程,方程的x、y、z分量分別對參數u求導數,由式(10)得到過控制頂點的曲線。

(2)確定預處理微線段的約束速度和減速點。在對微線段進行速度規劃時,通過實時前瞻處理預先獲取待加工路徑的運動信息,提前獲取加工路徑的約束速度和減速點，以便及時調整進給速度，避免發生過切。其實現過程如下：①根據式(19)確定過渡曲線的速度約束;②根據過渡曲線的實時插補長度，確定過渡曲線的減速點。采用迭代思想,根據下式得到實時插補長度:

L(ui)=L(ui-1)+|S(ui)-S(ui-1)|

(20)

式中,L(ui)為第i個插補周期的插補長度。

3　實驗驗證

為驗證所提出的過渡插補算法的有效性,采用自主研發的數控系統進行實驗驗證,該系統所采用的處理器為DSP28335,數控系統的插補周期為T=2ms,系統最大進給速度vmax=50mm/s,系統最大加速度amax=1000mm/s2,系統最大加加速度jmax=2m/s3。以加工由21段小線段組成的卡通小動物輪廓為例,其各點x軸和y軸的坐標值如表1所示,其加工路徑如圖5所示。

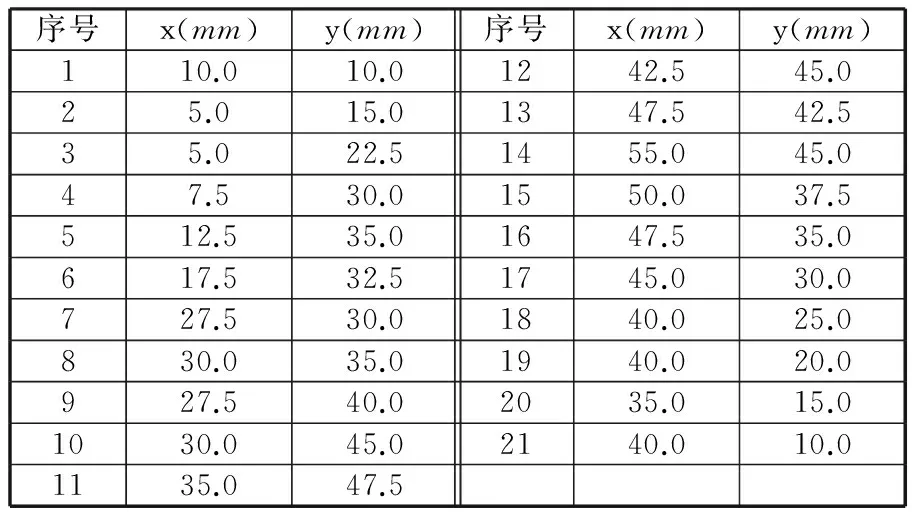
表1　卡通動物輪廓各點坐標

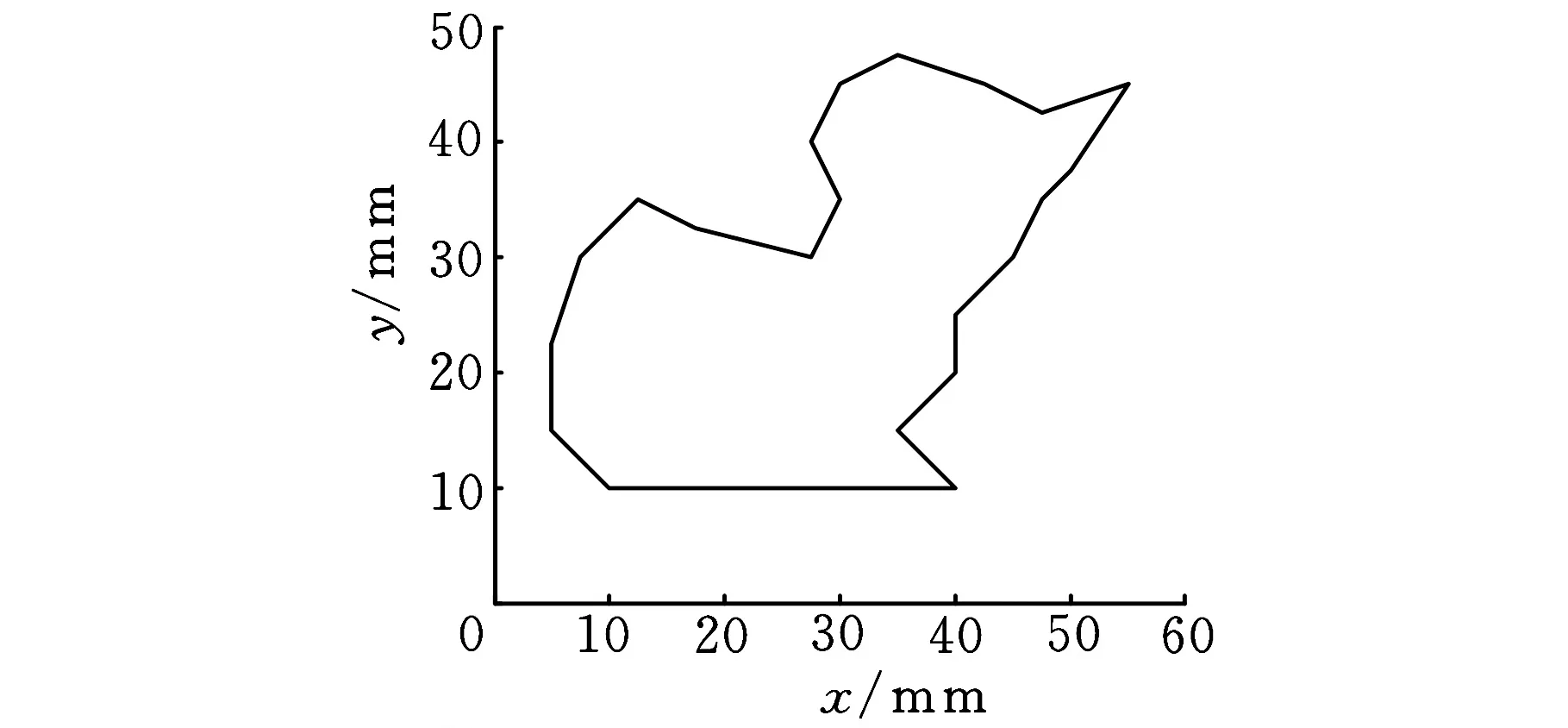
圖5　卡通動物輪廓加工路徑圖

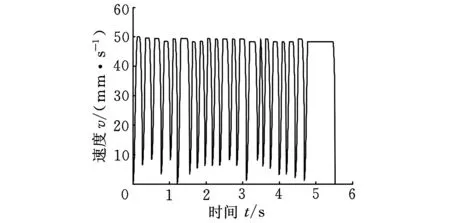
圖6　直接過渡法速度曲線

相鄰微線段間分別采用過控制頂點的二次曲線過渡方法和直接過渡法對微線段進行數控加工實驗。數控系統在速度規劃時,采用S形加減速控制方法,通過自主研發控制器中的數據采集模塊對實際輸出數據進行實時采集,采用MATLABR2009a軟件平臺進行數據處理，得到的結果如圖6和圖7所示。圖6為采用直接過渡方法得到的速度曲線,圖7為采用過控制頂點曲線過渡方法得到的速度曲線。通過分析圖6和圖7可知,兩種過渡方法的轉接速度波動不同,當采用直接過渡法對微線段進行數控加工時，其速度波動范圍為1.263～50.0mm/s,所耗費的加工時間為5.5s;當采用過控制頂點的曲線過渡方法時,其速度波動范圍為22.8～50.0mm/s,所耗費的加工時間為4.48s。因此,采用過控制頂點曲線進行過渡插補時,加工過程中速度波動較小,加工所用的時間較短。通過分析可知,影響直接過渡法的加工速度除了微線段自身特性外,還與數控系統的基本參數有關;影響過控制頂點曲線過渡方法的加工速度主要有弦高誤差、過渡曲線曲率半徑和插補周期等因素。因此，采用直接過渡法對微線段進行插補計算，由于轉接速度較小，在加工過程中頻繁地進行加減速，速度波動大，加工時間長；采用過控制頂點曲線過渡方法進行插補計算，由于轉接速度比較大，速度波動更小、加工速度更平穩、加工時間更短。因此，過控制頂點曲線過渡方法具有更好的運動平穩性，同時具有較高的加工效率，更適合于連續小線段的高速加工場合。

4　結論

(1)針對微線段數控加工過程中的轉接點的插補問題,為減小微線段加工的速度波動、實現加工速度平滑過渡,通過基于特征多邊形頂點曲線模型的幾何特性,構建微線段過控制頂點的過渡曲線數學模型。

(2)提出了一種基于過控制頂點曲線過渡插補算法。根據微線段幾何特征和加工精度要求，計算曲線過控制頂點的位置；根據特征多邊形頂點曲線的幾何特征、動力學分析和極限速度等條件,確定過渡曲線的約束速度；根據約束速度，采用實時前瞻處理方法對過渡曲線的進給速度進行自適應控制。

(3)實例對比驗證結果表明，所提出的方法在保證加工精度的條件下,有效地提高了微線段數控加工轉接速度，實現了平穩加工，同時縮短了加工時間。該算法適用于連續微線段高速加工場合。

[1]皮佑國,范德和.數控加工中連續微線段軌跡的B樣條曲線擬合[J].華南理工大學學報(自然科學版),2012,40(1):53-57.

PiYouguo,FanDehe.B-spineCurveFittingofConsecutiveMicro-segmentTrajectoryinNCMaching[J].JournalofSouthChinaUniversityofTechnology(NaturalScienceEdition),2012,40(1):53-57.

[2]張曉輝,于東,楊東升,等.面向微線段高速加工的拐角曲線過渡插補算[J].機械工程學報,2010,46(19):183-191.

ZhangXiaohui,YuDong,YangDongsheng,etal.CornerCurveTransitionInterpolationAlgorithmforHighSpeedMachiningofMicro-lineSegment[J].JournalofMechanicalEngineering,2010,46(19):183-191.

[3]ZhangLibing,YouYoupeng,HeJun,etal.TheTransitionAlgorithmBasedonParametricSplineCurveforHigh-speedMachiningofContinuousShortLineSegments[J].InternationalJournalAdvancedManufacturingTechnology,2011,52:245-254.

[4]王宇晗,肖凌劍,曾水生,等.小線段高速加工速度銜接數學模型[J].上海交通大學學報,2004,38(6):901-904.

WangYuhan,XiaoLingjian,ZengShuisheng,etal.AnOptimalFeedrateModelandSolutionforHigh-speedMachingofSmallLineBlockswithLook-ahead[J].JournalofShanghaiJiaotongUniversity,2004,38(6):901-904.

[5]YePeiqing,ShiChuan,YangKaiming,etal.InterpolationofContinuousMicroLineSegmentTrajectoriesBasedonLook-aheadAlgorithminHigh-speedMachining[J].InternationalJournalofAdvancedManufacturingTechnology,2008,37:881-897.[6]張立先,孫瑞勇,高小山,等.數控機床高速微線段插補算法與自適應前瞻處理[J].中國科學:技術科學,2011,41(6):774-789.

ZhangLixian,SunRuiyong,GaoXiaoshan,etal.HighSpeedInterpolationforMicro-lineTrajectoryandAdaptiveReal-timeLook-aheadinCNCMachining[J].ScienceChinaTechnologicalSciences,2011,41(6):774-789.

[7]何均,游有鵬,陳浩,等.連續短線段空間圓弧轉接與插補[J].航空學報,2010,31(5):1086-1092.

HeJun,YouYoupeng,ChenHao,etal.AnInterpolatorforContinuousShort-segmentsBasedonSpaceArcTransition[J].ActaAeronauticaetAstronauticaSinica,2010,31(5):1086-1092.

[8]何均，游有鵬，王化明.面向微線段高速加工的Ferguson樣條過渡算法[J]. 中國機械工程，2008，19 (17): 2085-2089.

HeJun,YouYoupeng,WangHuaming.AMicro-lineTransitionAlgorithmBasedonFergusonSplineforHighSpeedMachining(HSM)[J].ChinaMechanicalEngineering,2008,19(17):2085-2089.

[9]LiW,LiuYD,YamazakiK.TheDesignofaNURBSPre-interpolatorforFive-axisMachining[J].InternationalJournalofAdvancedManufacturingTechnology,2008,36:927-935.

[10]WangJunbin,YauHT.Real-timeNURBSInterpolator:ApplicationtoShortLinearSegments[J].InternationalJournalAdvancedManufacturingTechnology,2009,41:1169-1185.

[11]沈斌,齊黨進,樊留群,等.基于NURBS曲線擬合的微段高速自適應加工算法[J].中國機械工程,2012,23(15):1825-1829.

ShenBin,QiDangjin,FanLiuqun,etal.High-speedAdaptiveInterpolationAlgorithmBasedonNURBSFittingforMicroSections[J].ChinaMechanicalEngineering,2012,23(15):1825-1829.

[12]YauHT,WangJunbin.FastBezierInterpolatorwithReal-timeLook-aheadFunctionforHigh-accuracyMachining[J].InternationalJournalofMachineTools&Manufacture,2007,47(1):1518-1529.

[13]任錕,傅建中,陳子辰.高速加工中速度前瞻控制新算法研究[J].浙江大學學報(工學版),2006,40(6):1985-1988.

RenKun,FuJianzhong,ChenZichen.NewLook-aheadAlgorithmforVelocityControlinHighSpeedMaching[J].JournalofZhejiangUniversity(EngineeringScience),2006,40(6):1985-1988.

(編輯王艷麗)

Transition Interpolation Algorithm for Micro-line Segments Based on Curve through Control Points

Wu TingZhang LibingHuang Fengli

Jiaxing University,Jiaxing,Zhejiang,314001

In order to reduce the velocity fluctuations and realize smoothing transition for machining of micro line segments,an interpolation algorithm was presented based on curve though control points.The curve transition vector model of micro-line segments was constructed.On the basis of geometric characteristics of curve model based on the characteristic polygon vertex,a vector model was proposed based on curve transition through control points.Interpolation of micro-line segments were calculated by using vector model based on the curve transition according to the machining errors and geometric characteristics of the curve,values of control vertex were calculated,the constraint velocity was determined,and real-time look-ahead control was processed.The proposed method was evaluated by an experiment,and experimental results demonstrate that the algorithm can effectively improve transition speed of the micro-line segments,shorten the machining time,and achieve smooth transition.

CNC machining;micro-line interpolation;curve transition;look-ahead control;curve through control points

2015-01-20

國家自然科學基金青年科學基金資助項目(51405197);浙江省自然科學基金資助項目(LQ14E050006,LY13E050021);嘉興市科技計劃資助項目(2013AY11020);“十二五”浙江省高校重點學科資助項目

TH162;TP273DOI：10.3969/j.issn.1004-132X.2015.10.015

吳婷,女,1979年生。嘉興學院機電工程學院講師、博士。主要研究方向為數字化設計與制造、數控技術。發表論文20余篇。張禮兵,男,1974年生。嘉興學院機電工程學院講師。黃風立,男,1976年生。嘉興學院機電工程學院副教授、博士。