垂直平面三桿柔性機械手動力學建模及仿真

田　穎　張建華　張明路

河北工業大學,天津,300130

垂直平面三桿柔性機械手動力學建模及仿真

田穎張建華張明路

河北工業大學,天津,300130

為解決柔性機械手動力學建模常用的有限元等方法導致模型精度不高的問題,將柔性機械手視為連續整體,用矢量法建立了機械手的動力學模型。對比了矢量法和FEM法建立的動力學模型以及理想狀態下機械手剛體動力學模型的仿真結果。對比結果表明，用矢量法建立的柔性機械手動力學模型是可行的,精度也較高。

柔性機械手;矢量法;動力學;Lagrange方程

0　引言

機械手柔性對其末端運動軌跡有一定影響,并且機械手桿件越長,柔性變形越不可忽略。因此對輕質柔性機械手的研究成為機器人領域研究的熱點。對于由輕質桿件組成的機械臂來說,常用的動力學研究方式分為三種:質量集中法、假定模態法(AMM)與有限元法(FEM)。

質量集中法是建立柔性機械手動力學模型的最簡單方法，但建立的模型精度較低。AMM與FEM的核心思想是將桿件離散為有限個剛性體組成的系統，使用這兩種方法建立的動力學模型其精度較質量集中法有所提高,但應用范圍較小[1]。Priyanka等[2]使用AMM進行了單桿機械手動力學分析，用浮動切線坐標系定義桿件上的點位置，并給出了仿真結果。但該方法僅適合于簡單機械手系統，多用于單桿勻質機械手。桿件數目增加或是桿件截面不規則時，確定模態難度很大，AMM不再適用。FEM與AMM相比，其適用范圍有所擴大。Shin等[3]闡述了應用FEM的兩桿機械手的動力學建模過程,但未能進行仿真。Wen[4]研究了三桿及三桿以上機械手的動力學分析，給出了仿真結果。FEM的缺點在于它的精度依然不高,而且該方法適宜在平面運動的機械手,不能滿足空間機械手的建模要求。Vicente等[5]應用矢量法對單桿機械手進行動力學分析，并以此為基礎進一步建立了控制模型，驗證了該方法的可行性。Masoud等[6]從建立數學模型的角度證明了矢量法應用于三桿以上的多桿機械手的動力學分析的可行性，但是僅針對多桿機械手中的某一桿件進行了仿真實驗,沒有得出以多桿機械手作為整體的機械手系統仿真結果。本文針對以上情況,以垂直平面三桿機械手為例,討論如何應用矢量法建立柔性機械手動力學模型，并通過仿真對比驗證分析柔性機械手運動情況。

1　垂直平面三桿柔性機械手的簡化

本文以勻質剛性鉸接的三桿機械手為例,對其進行簡化。由于機械手運動過程中的縱向變形和扭曲變形遠小于橫向變形，可以認為桿件只有橫向變形，且變形前后桿件兩端直線距離保持不變。圖1所示為垂直平面三桿機械手簡化模型。其中,θ1、θ2、θ3分別為理想剛性臂與水平地面的夾角;M1、M2、M3分別為第一關節、第二關節和末端的負載;L1、L2、L3分別為三連桿的長度;τ1、τ2、τ3為機械臂的轉矩。從圖1可以看出，機械手的獨立坐標變量應當包括θ1、θ2、θ3和各桿件的橫向變形。

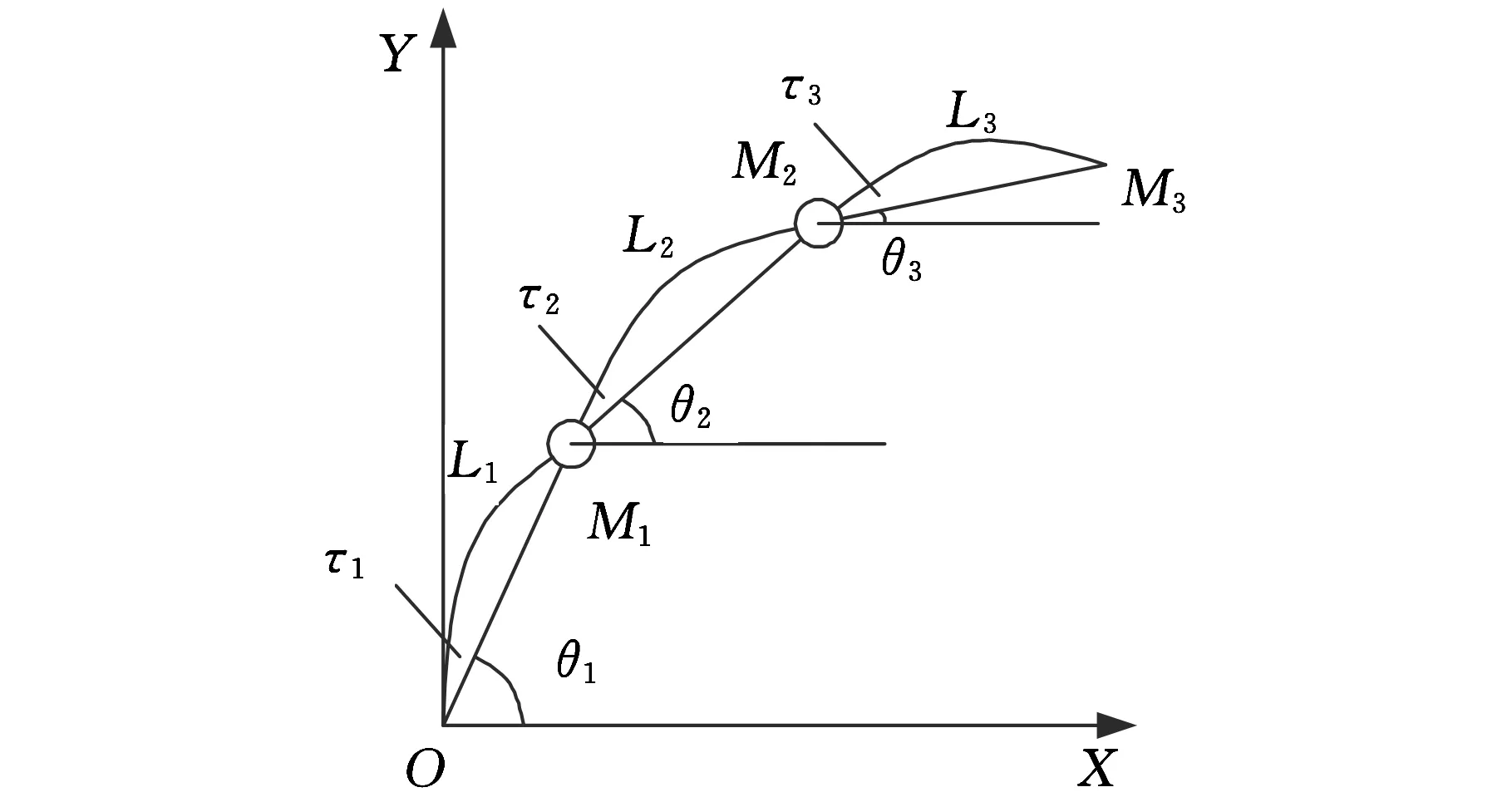
圖1　三桿機械手簡化模型

2　矢量法的機械手動力學模型

2.1柔性機械手能量計算

FEM和AMM法對柔性機械手的動能和勢能的處理如下:先將柔性構件離散為有限個剛性構件，再將剛性構件的能量分別計算累積求和,因此在離散過程中會產生一定的誤差。矢量法將桿件視為柔性整體，從源頭上避免了這一問題的出現。

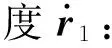
則桿1的動能為

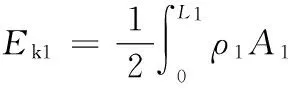
(1)

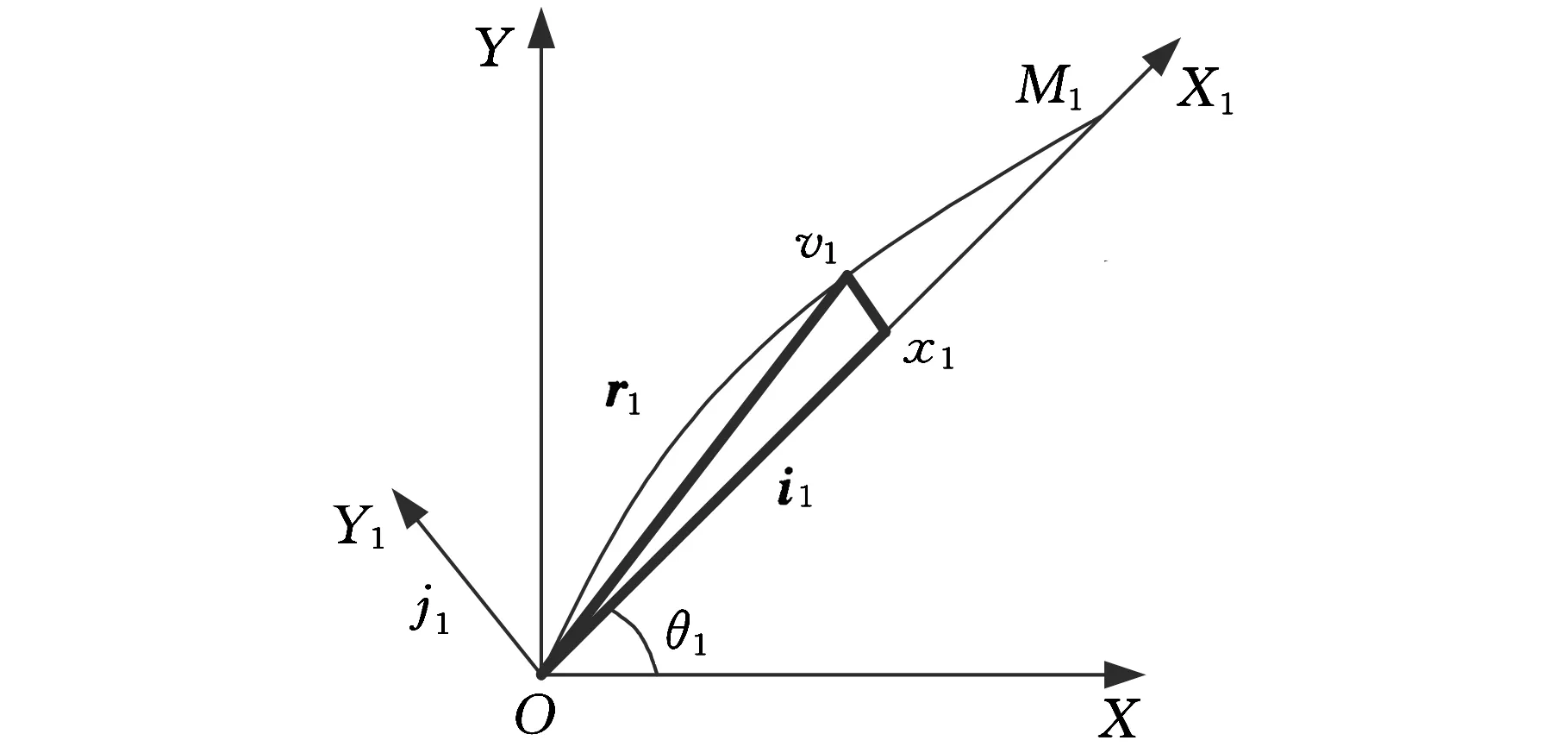
圖2　桿1彈性變量示意圖

圖3中桿2任一點矢量表示為

則桿2的動能為

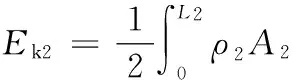
(2)

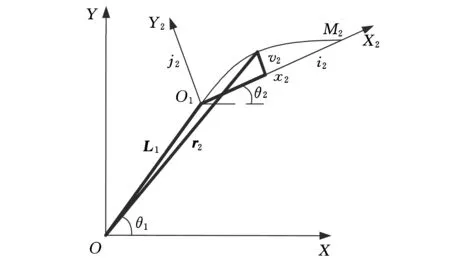
圖3　桿2彈性變量示意圖

依此類推,桿3的任一點矢量為

桿3的動能為

(3)

式(1)～式(3)中,單位向量的運算關系滿足：

k,m=1,2,3且k≠m

則柔性機械手系統的動能之和為

Ek=Ek1+Ek2+Ek3

(4)

第i(i=1,2,3)桿的彈性勢能為

(5)

vi=φi1(xi)qi1+φi2(xi)qi2

φij(xi)=sin(jπxi/Li)i=1,2,3;j=1,2

式中,EiIi為第i桿的彎曲剛度;vi為第i桿上任一點的橫向變形;φi j(xi)為振型函數,下標i、j分別表示第i桿和j階彈性模量;qi1、qi2分別為一階和二階彈性模態的時間函數,與桿件轉動角度一起,組成了矢量法中的獨立坐標變量。

基于以上彈性勢能公式的推導，可得三桿機械手彈性勢能之和：

Ep=Ep1+Ep2+Ep3

(6)

平面三桿柔性機械手的重力勢能簡化為每桿重力等效在變形后的桿件中點產生的重力勢能。則桿1的重力勢能為

W1=(m1|r1(L1/2)|+M1L1)gsinθ1

(7)

桿2的重力勢能為

W2=m2gsin(θ1+θ2)|r2(L2/2)|+

M2g(L1sinθ1+L2sinθ2)

(8)

桿3的重力勢能為

W3=m3gsin(θ1+θ2+θ3)|r3||x3=L3/2+

M3g(L1sinθ1+L2sinθ2+L3sinθ3)

(9)

三桿機械手系統的重力勢能為

W=W1+W2+W3

(10)

由于柔性機械臂是一個非保守系統，其能量公式可應用于Lagrange方程：

(11)

L=Ek-(Ep+W)

機械手系統獨立坐標變量為

在不考慮重力的影響下,系統所作的虛功為

(12)

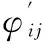
通過式(12)可以求得系統廣義力Qn。

2.2三桿機械手動力學方程的符號推導

式(11)經過整理后，可得柔性機械手的顯式動力學方程：

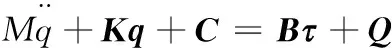
(13)

L1L2(M2+2m3+M3)cos(θ1-θ2)-

m2L1L2(2q21+q22)sin(θ1-θ2)/π

m51=m15=-2ρ2A2l1cos(θ1-θ2)

m71=m17=(m3L3+M3)L1L3cos(θ1-θ3)-

m3L1L3(2q31+q32)sin(θ1-θ3)/π

m81=m18=-2m3L1L3cos(θ1-θ3)/π

m91=m19=-m3L1L3cos(θ1-θ3)/π

m22=m33=m1L1

m47=m74=L2L3(m3L3+M3)cos(θ2-θ3)-

m3L2L3(2q31-q32)sin(θ2-θ3)/π

m48=m84=-2m3L2L3cos(θ2-θ3)/π

m49=m94=-m3L2L3cos(θ2-θ3)/π

m55=m66=m2L2

m88=m99=m3L3

3　剛性機械手動力學建模

垂直平面三桿剛性機械手自由度為3,其廣義坐標變量

qg=[θ1gθ2gθ3g]T=[q1gq2gq3g]T

剛性三桿機械手動能為

(14)

三桿剛性機械手勢能為

Wg=(m3/2+M3)gL3sinθ3g+

(m2/2+m3+M2+M3)gL2sinθ2g+

(m1/2+m2+m3+M1+M2+M3)gL1sinθ1g

(15)

由于剛性機械臂是一個非保守系統,其能量公式可應用于Lagrange方程：

(16)

Lg=Ekg-Wg

整理式(16)可得三桿剛性機械手的顯式動力學方程：

(17)

mg33=m3L3

4　仿真結果比較與分析

通過比較矢量法、FEM法建立的柔性機械手動力學模型和剛性機械手動力學模型仿真結果,可以判斷矢量法的可行性并定性分析矢量法建模的精度。

表1所示為柔性三桿機械手的仿真參數,除彎曲剛度EiIi外,其余仿真參數也應用于剛性三桿機械手的仿真。

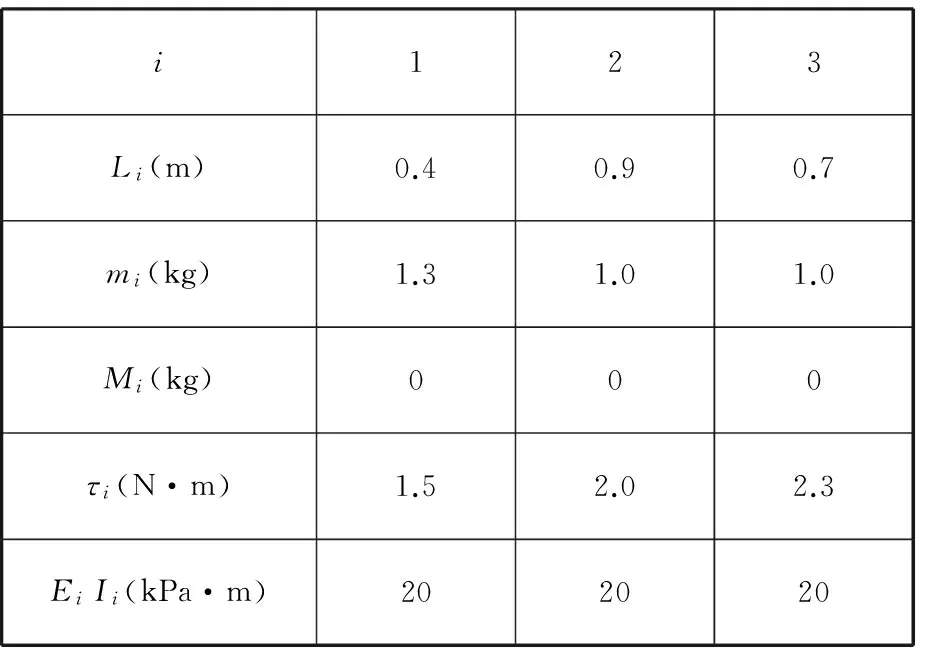
表1　三桿機械手參數值

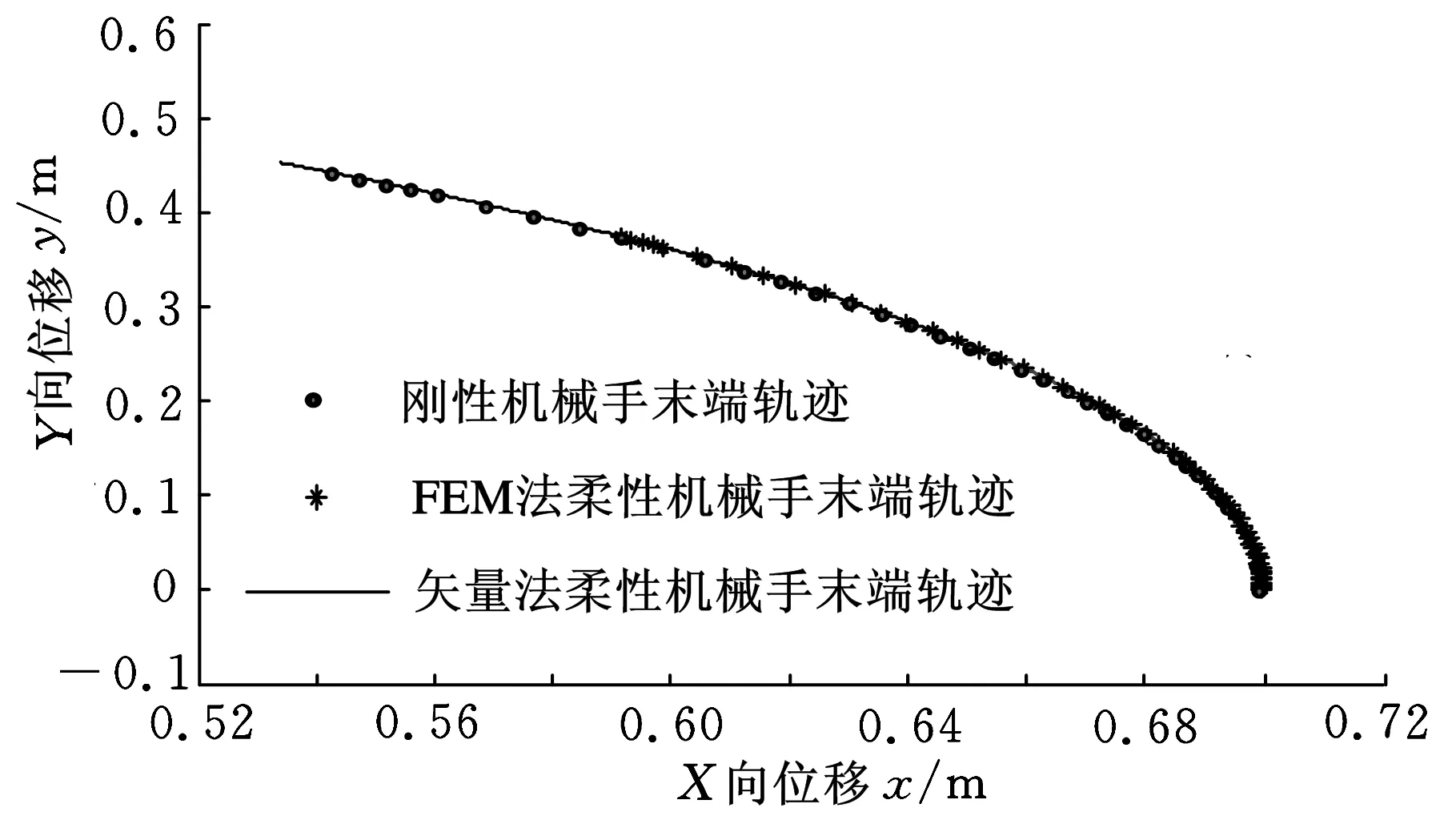
圖4　柔性與剛性機械手末端運動軌跡

圖4所示為使用矢量法、FEM法的柔性機械手末端運動軌跡仿真結果與理想剛性機械手末端運動軌跡仿真結果。由圖4可以看出,在表1所示條件下,機械手的柔性變形較大,不可忽略。矢量法和FEM法的軌跡較為吻合,證明矢量法可行。

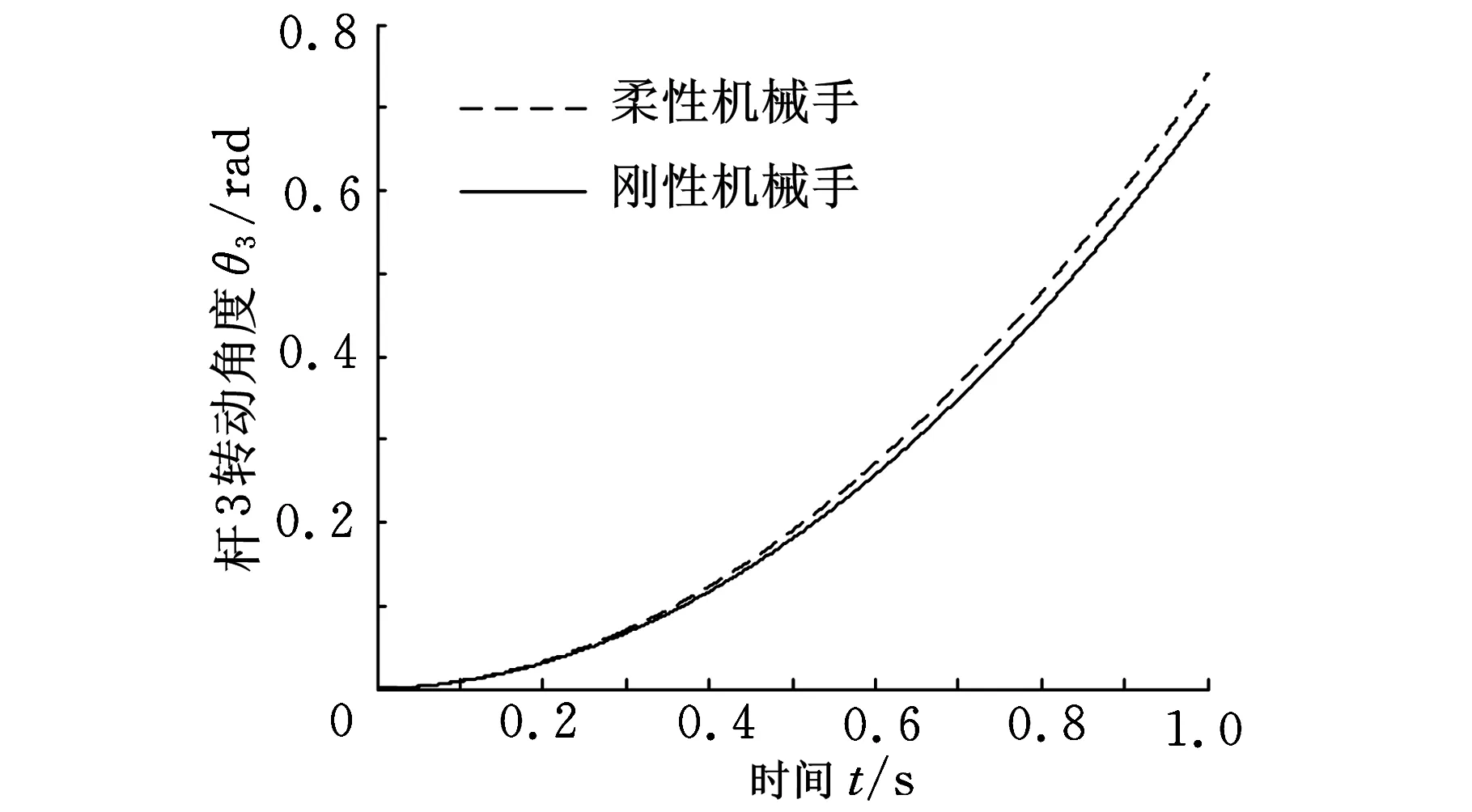
圖5　桿3的轉動角度仿真結果

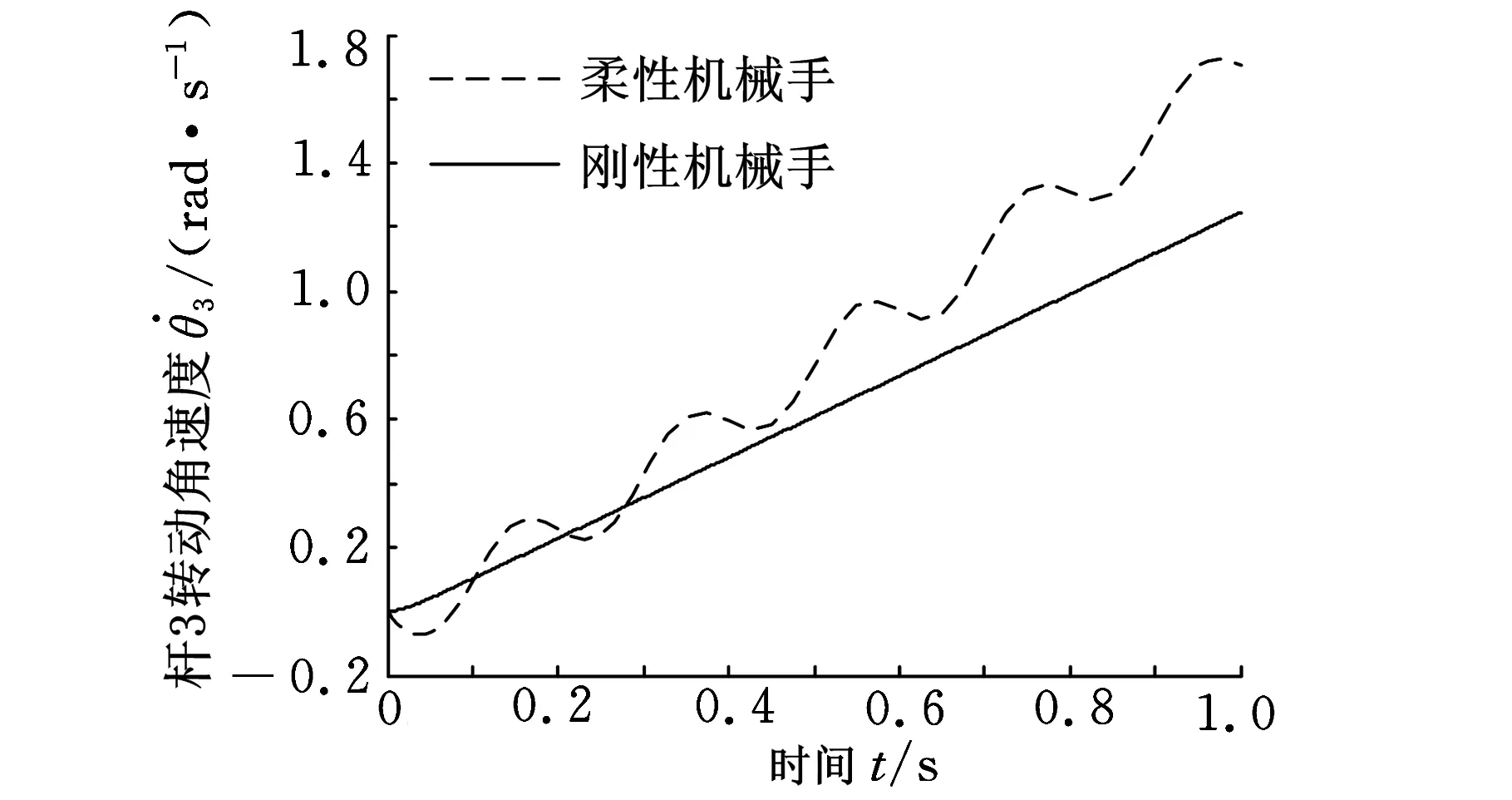
圖6　桿3的轉動角速度仿真結果

由圖7、圖8可以看出，柔性機械手的橫向變形較小，最大值小于0.4mm,這符合機械手實際運動情況。對于剛度較大的桿件材料和結構，其彈性變形較小，通常情況下可以忽略，但對于高精度要求下的機械手作業，該變形不能忽略。

圖7　柔性機械手桿3的一階橫向變形

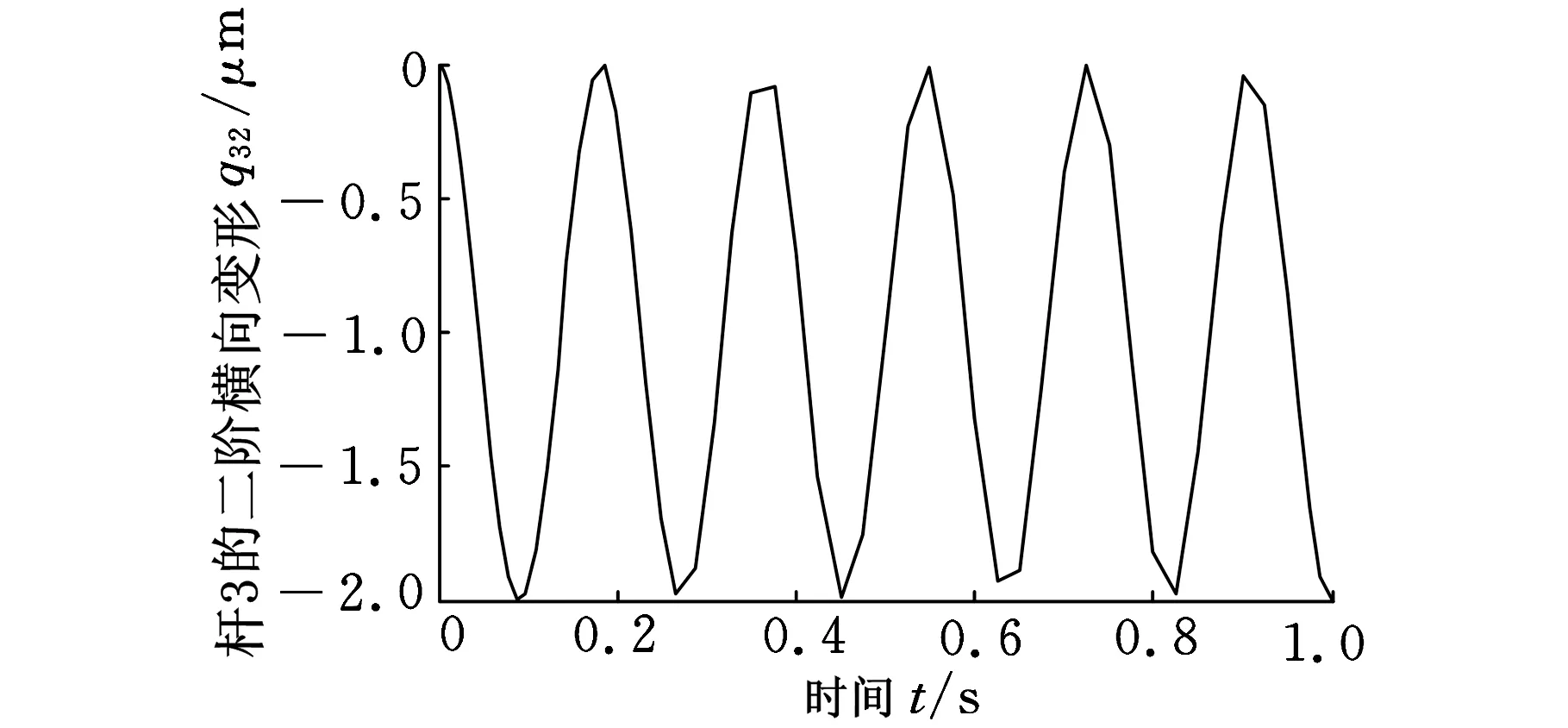
圖8　柔性機械手桿3的二階橫向變形

5　結語

用矢量法建立的垂直平面三桿柔性機械手系統的動力學模型,具有計算精度高、計算復雜程度低的特點。剛性機械手和柔性機械手的仿真結果對比證明了該模型的可行性。柔性機械手的仿真結果還表明,對于剛度較小、精度要求較高的柔性機械手,其柔性變形已不能忽略,機械手系統如果繼續作為理想剛性機械手處理會引起較大誤差。

但矢量法也有其缺點,由第二節建立動力學模型的過程可以看出,大量的符號運算提高了計算精度,但導致數據的計算較為繁瑣，如何在提高模型精度的基礎上進一步簡化計算過程，是矢量法建模今后的研究方向。

[1]Santosha K D,Peter E.Dynamic Analysis of Flexible Manipulators,a Literature Review[J].Mechanism and Machine Theory,2006,41(7):749-777.

[2]Priyanka M,Qiao Sun,Yoshikazu Kanamiya.A Pseudo-rigid Model for the Inverse Dynamics of an Euler Beam[J].Applied Mathematical Modelling,2011,35(8)：3854-3865.

[3]Shin Ho-Cheol,Choi Seung-Bok.Position Control of a Two-link Flexible Manipulator Featuring Piezoelectric Actuators and Sensors[J].Mechatronics,2001,11(6):707-729.

[4]Wen Chen.Dynamic Modeling of Multi-link Flexible Robotic Manipulators[J].Computers and Structures,2001,79(2)：183-195.

[5]Vicente F,Emiliano P,Iván M D.Passivity-based Control of Single-link Flexible Manipulators Using a Linear Strain Feedback[J].Mechanism and Machine Theory,2014,71:191-208.

[6]Masoud M,Mostafa G,Mohammad J S.A Nonlinear High Gain Observer Based Input-output Control of Flexible Link Manipulator[J].Mechanics Research Communications,2012,45:34-41.

(編輯張洋)

Dynamics Modeling and Simulation of Three-link Flexible Manipulator on Vertical Plane

Tian YingZhang JianhuaZhang Minglu

Hebei University of Technology,Tianjin,300130

For solving problem of lower accuracy induced by common methods in flexible manipulator dynamics modeling,such as FEM etc.,flexible manipulator was considered as a continuous whole and its dynamics model was built by vector method.Simulation results of dynamics model of flexible manipulator under vector method and FEM,and dynamic model of ideal rigid manipulators were compared to prove that vector method is effective and more accurate.

flexible manipulator;vector method;dynamics;Lagrange equation

2013-09-09

TH113.22DOI：10.3969/j.issn.1004-132X.2015.08.005

田穎，女，1987年生。河北工業大學機械工程學院博士研究生。主要研究方向為機器人動力學及控制。張明路，男，1964年生。河北工業大學機械工程學院教授、博士研究生導師。張建華，男，1979年生。河北工業大學機械工程學院副教授。