基于動態系數法的微型渦噴發動機實時建模
徐 鑫 張天宏 盛漢霖
南京航空航天大學江蘇省航空動力系統重點實驗室,南京,210016
基于動態系數法的微型渦噴發動機實時建模
徐鑫張天宏盛漢霖
南京航空航天大學江蘇省航空動力系統重點實驗室,南京,210016
利用時域法系統辨識獲得了發動機一系列穩態點附近的轉速-燃油量穩態特性和動態特性,通過插值算法獲得了全范圍穩態關系和加速度系數,采用動態系數法建立了發動機全范圍實時模型。該模型結構簡單,運算量較小,實時性好。仿真試驗表明:該模型可以較好地反映微型渦噴發動機的穩態特性和動態特性,與試驗數據相比,模型的穩態點誤差不超過1%,過渡過程誤差不超過6%,可用于微型渦噴發動機的容錯控制。
微型渦噴發動機;容錯控制;系統辨識;動態系數法;實時模型
0 引言
微型渦噴發動機控制系統傳感器的穩定性對于保證發動機全權限數字電子控制系統正常工作至關重要[1]。針對微型渦噴發動機傳感器故障診斷與容錯控制的需求,本文建立了用于故障診斷的發動機實時機載模型。
目前,國內外常用的發動機建模方法有解析法和試驗法[2-6]。解析法建模先根據氣動熱力學公式,結合部件特性和工作狀態,建立發動機非線性部件級模型,再根據臺架試車數據或試飛數據對其進行修正[7]。用解析法建立的模型一般比較精確,但由于算法復雜,迭代量較大,從而使得解析法建立的模型運算耗時太長,甚至導致模型運算不收斂,故不適合作為機載實時模型。試驗法建模根據發動機系統的輸入輸出數據關系建立模型,將發動機整體看作“黑箱”或“灰箱”,傳統試驗法建立的模型雖然實時性較好,但模型的精度低,難以在全包線范圍內模擬發動機的穩態和動態特性[8-10]。
為了建立精度高、實時性好、可在全包線范圍內模擬發動機各種工況的微型渦噴發動機模型,本文在試驗法的基礎上,提出了一種新的建模思路[8],即根據發動機臺架試車數據,運用系統辨識、插值算法和動態系數法建立微型渦噴發動機模型。由于發動機起動過程比較復雜,故本文主要研究發動機起動過程以上工作狀態(起動過程模型利用最小二乘法擬合得到)。起動過程以上工作狀態建模過程如下:首先利用時域系統辨識法[11-12]獲得發動機一系列穩態點附近的轉速-燃油流量穩態特性和動態特性,通過插值算法獲得全范圍穩態關系和加速度系數,采用動態系數法建立發動機全范圍實時模型;然后利用實時模型對微型渦噴發動機開展從慢車狀態到最大狀態的數值仿真。仿真結果與原始試車數據的比較結果表明,該模型具有較好的穩態和動態精度,可以用作傳感器故障診斷機載模型。
1 建模數據的獲取與預處理
由于發動機具有非線性特點,所以應通過臺架試驗得到發動機運行過程中不同工作點的輸入輸出數據,試驗臺如圖1所示。本文用油泵電壓占空比來控制燃油流量,經過多次試驗測試,在相同工作狀態下,油泵電壓占空比與燃油流量之間為固定的線性關系,故將燃油流量作為輸入,將發動機轉速作為輸出。

圖1 發動機試車臺
為了準確獲得發動機的動態特性,必須對其進行動態激勵。本文采用的激勵措施為在各個穩態工作點附近加入M序列信號。本文選取5級線性移位寄存器的M序列信號[10],其步長為0.2 s,幅值為輸入信號最大幅值的5%。激勵的具體實驗步驟為先將發動機運行至慢車狀態,之后在各個穩態工作點施加4~5個周期的M序列激勵,圖2所示為70 000 r/min下的動態試車曲線,轉速信號的采樣周期為20 ms。
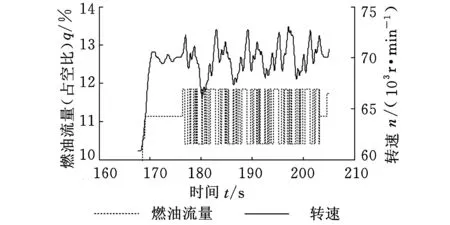
圖2 發動機轉速在70 000 r/min的試車數據
由試車數據可以獲取各個穩態工作點的燃油流量與發動機轉速穩態關系,以及穩態工作點附近的燃油流量與發動機轉速動態關系。
下面利用野點剔除、濾波、相似變換以及歸一化等方法對原始試車數據進行預處理。
以燃油流量為橫坐標,穩態轉速為縱坐標,得到發動機轉速-燃油流量穩態特性曲線。參照該曲線,對明顯偏離曲線的個別數據進行修正或直接舍去;對慢車以上動態曲線進行濾波處理,以提高原始試驗數據的有效性。
為了建立適用于全包線范圍內發動機動態仿真的數學模型,需對原始試車數據進行相似變換,將其換算至標準大氣狀況(p0=101 325 Pa,T0=288.15 K)下,以便將其用于不同大氣條件的發動機模型計算。在環境溫度為T1、環境壓力為p1的大氣條件下,發動機轉速n、燃油流量q的換算公式如下[13]:
(1)
(2)
將得到的相似參數進行歸一化處理:
ncor=nc/nc,max
(3)
qcor=qc/qc,max
(4)
式中,下標max表示最大值。
2 動態系數法
2.1動態系數的物理意義
根據微型渦噴發動機穩態轉速與燃油流量的對應關系,采用一維插值法,建立其穩態模型:
(5)
式中,f(*)為一維插值函數,φ(*)=f-1(*);下標s代表穩態。
發動機在動態工作過程中,若t時刻轉速為n(t),燃油流量為q(t),定義當前剩余燃油流量為
Δq=q(t)-φ(n(t))
(6)
Δq>0即燃油流量有剩余時,渦輪產生的功率大于壓氣機所需功率,發動機將加速;Δq<0即燃油流量減少時,渦輪產生的功率小于壓氣機所需功率,發動機將減速。Δq越大,發動機加速或減速得越快。由此可見,發動機的轉速變化量與剩余燃油量存在某種關系,用燃油加速度動態系數C來量化此關系,即
C=Δn/(ΔqΔt)
(7)
式中,Δn為剩余燃油流量產生的轉速增量;Δt為采樣周期。
2.2動態系數的獲取
下面采用系統辨識法推導出動態系數[9]。由于發動機內部的氣動熱力學過程比較復雜,為了簡化發動機模型公式的推導,特作以下假設:①只考慮發動機轉子慣性對發動機動態特性的影響,忽略熱慣性和部件通道容積動力學的影響;②只研究發動機在其穩態點附近的小偏離運動,并認為動態過程中,部件效率及總壓損失系數保持不變;③臺架試車環境條件不變;④燃油泵不由發動機帶動,而是由控制器驅動;⑤忽略燃燒延遲及燃氣與空氣流量的差別。
根據假設①,描述發動機動態特性的方程就是發動機轉子的動態力矩平衡方程,即
Jdω/dt=ΔM=MT-MC
(8)
式中,J為微型渦噴發動機轉子的轉動慣量,kg·m2;ω為微型渦噴發動機轉子的角速度,rad/s;ΔM為作用在轉子軸上的外力矩之和即剩余力矩,N·m;MT為渦輪扭矩,N·m;MC為壓氣機扭矩,N·m。
根據微型渦噴發動機的工作原理,渦輪扭矩MT和壓氣機扭矩MC是轉速n、燃油流量q和外界干擾量d的函數。假設d=0,則
MT=MT(n,q)
(9)
MC=MT(n,q)
(10)
對式(9)、式(10)按Talor公式展開為冪級數,并只取級數的一次項,得到線性函數,即將式(9)和式(10)在穩態點附近線性化,得
MT=MTs+ΔMT=
(11)
MC=MCs+ΔMC=
(12)
穩態時,渦輪扭矩等于壓氣機扭矩,即MTs=MCs=Ms。
將式(11)、式(12)代入式(8),得
(13)
為了分析方便,通常采用相對增量即參數的絕對增量與基準值之比的形式進行計算。基準值可以選取原穩定狀態參數值或取最大狀態穩態值等。令轉速的相對增量δn=Δn/nb,燃油量的相對增量δq=Δq/qb,下標b表示基準值,將二者代入式(13),得
Td(δn)/dt+δn=Kδq
(14)
式中,T為微型渦噴發動機基本時間常數;K為微型渦噴發動機基本放大常數。
將式(14)在零初始條件下進行拉氏變換,得微型渦噴發動機的傳遞函數:
(15)
式(15)為微型渦噴發動機簡化后最基本的數學模型。由式(15)可知,微型渦噴發動機的基本簡化數學模型為無零點的一階系統,即慣性環節。t=0、δn=0的條件下,輸入δq為階躍量時,動態方程(式(14))的解為
δn=K(1-e-t/T)δq
(16)
對式(16)兩邊同時求導,得
d(δn)/dt=Ke-t/Tδq/T
(17)
根據假設②,微型渦噴發動機只在原平衡狀態附近做小偏離運動,原平衡狀態點即為t=0的時刻。于是,式(17)可以變形為
(18)
本文通過MATLAB自帶的系統辨識工具箱,將燃油流量作為輸入,將轉速作為輸出,選擇一階慣性環節作為辨識的傳遞函數模型,可快速地求得T和K。則發動機當前時刻轉速為
n(t)=n(t-1)+C(t)(q(t)-φ(n(t-1))Δt
(19)
式中,C(t)可由上一時刻轉速n(t-1)插值得到。
在每個穩態點,利用系統辨識算法得到此狀態下的T和K,根據式(18)計算出燃油加速度動態系數。將各穩態點的系數組合在一起,形成動態系數插值表(表1),供一階模型插值調用。
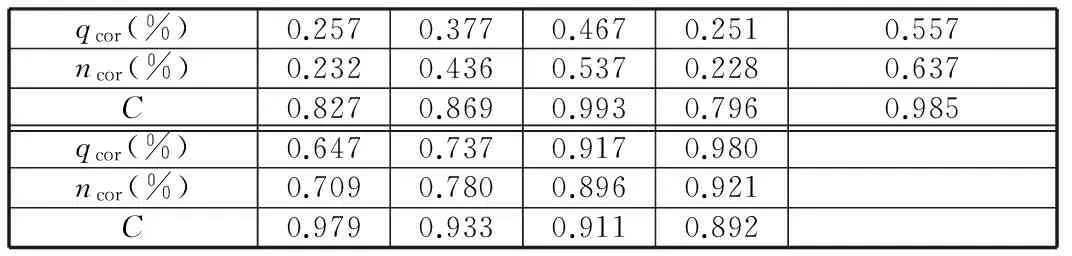
表1 動態系數插值表
3 模型仿真及結果分析
根據已得到的動態系數插值表,采用MATLAB進行編程,建立發動機數學模型。隨機選取2組原始臺架試車數據,對實時模型進行驗證并檢驗建模誤差。模型仿真結果如圖3、圖4所示。

(a)仿真與試車對比曲線
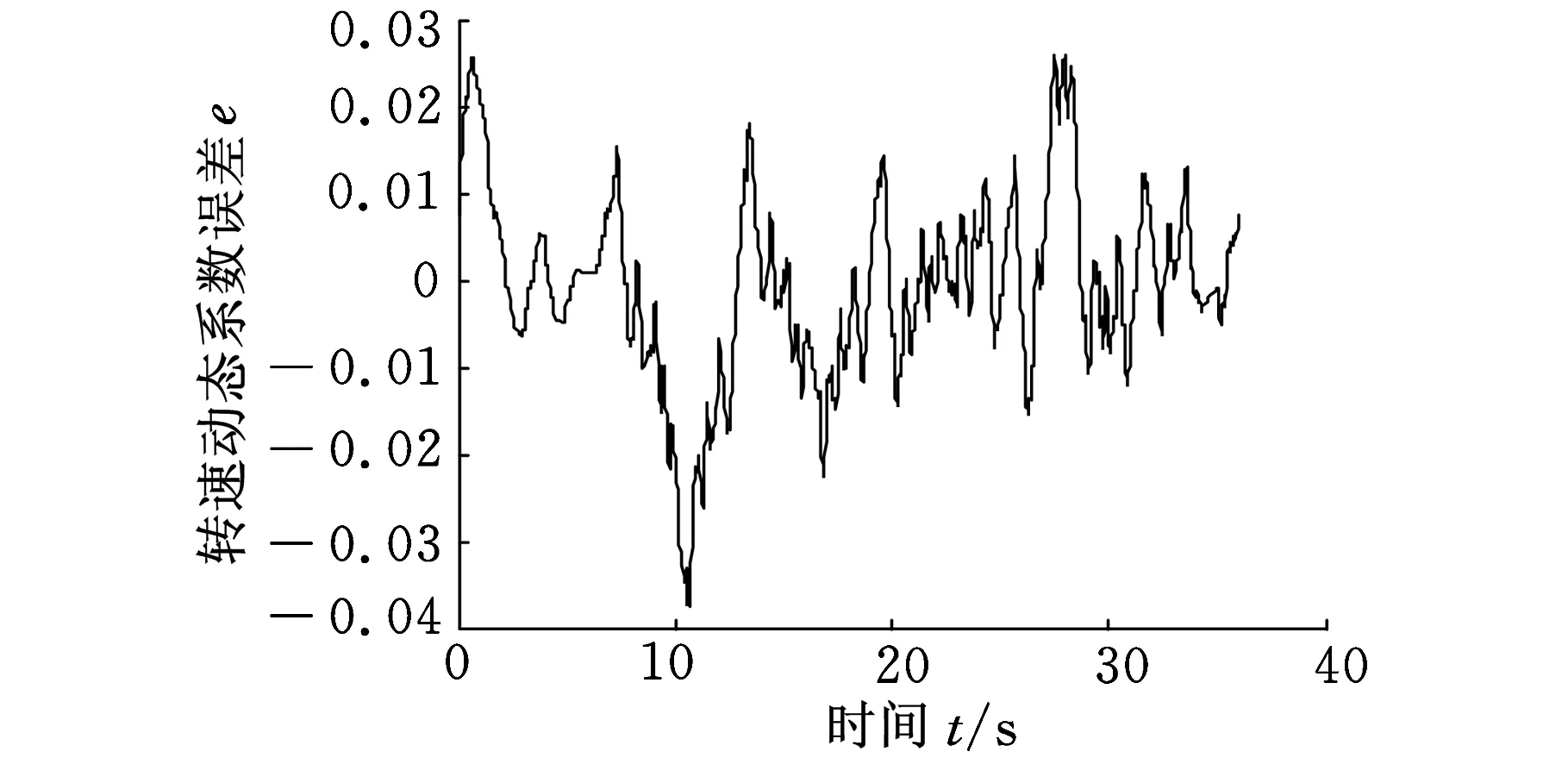
(b)誤差曲線圖圖3 發動機模型在70 000 r/min仿真結果
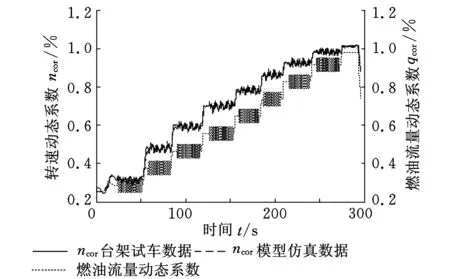
(a)仿真與試車對比曲線
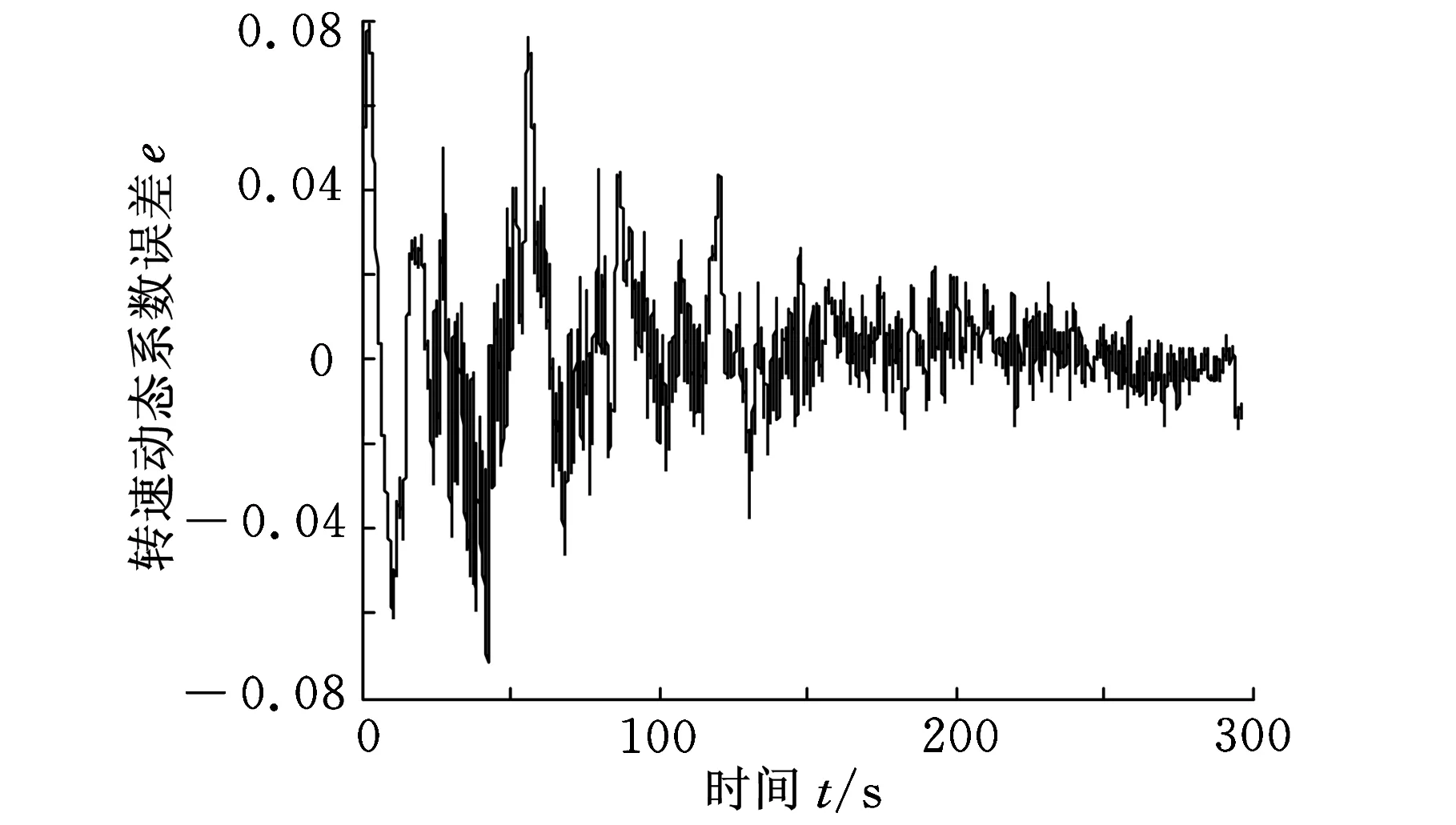
(b)誤差曲線圖圖4 發動機模型在30 000 r/min以上仿真結果圖
定義轉速的仿真誤差為
e=(ne-n)/n
(20)
式中,ne為各轉速模型仿真值;n為轉速實際采集值。
由于篇幅所限,這里只給出了部分的仿真曲線圖。從圖3、圖4可以看出,仿真結果與試車數據一致,說明本文所采用的方法是可行的。仿真精度達到了預期要求,模型穩態點誤差不超過1%,過渡過程誤差不超過6%,可作為控制系統傳感器故障診斷的發動機模型。
進一步將該模型嵌入到以主頻100MHz的DSP芯片TMS320F2808為核心的電子控制器中進行測試,利用定時器測試出模型單步運行時間僅需0.2ms,這對于以20ms為控制步長的發動機容錯控制器來說已具有極好的實時性。
4 結語
本文建立的微型渦噴發動機實時模型算法簡單,采用系統辨識、插值算法和動態系數法,可有效避免傳統部件級建模所必需的迭代計算,大大縮短了仿真時間,易于嵌入到發動機電子控制器中。本文采用的動態系數法可維護性強,當發動機更換或通過試驗得到更精確的穩動態試驗數據后,可通過本文所述的方法獲得動態系數,修改插值數據滿足模型更新的要求。本文只針對轉速建立了發動機轉速-燃油關系的動態模型,可用類似的方法針對燃氣溫度、推力等其他參數建立相應的模型。
[1]孫健國.面向21世紀航空動力控制展望[J].航空動力學報,2001,16(2):97-102.
SunJianguo.ProspectsoftheAeroengineControlDevelopmentintheEarlyTimeofthe21stCentury[J].JournalofAerospacePower,2001,16(2):97-102.
[2]DanieleCJ,KroselSM,SzuchJR,etal.DigitalComputerProgramforGeneratingDynamicTurbofanEngineModels,NASATM283446[R].Cleveland,Ohio:LewisResearchCenter,1983.
[3]KimJH,SongTW,KimTS,etal.ModelDevelopmentandSimulationofTransientBehaviorofHeavyDutyGasTurbines[J].JournalofEngineeringforGasTurbinesandPower,2001,12(3):589-594.
[4]李家瑞.航空發動機建模技術研究[D].南京:南京航空航天大學,2005.
[5]張建良,秦琦峰,黃向華,等.小型航空二沖程活塞發動機建模及控制器在回路仿真研究[J].中國機械工程,2013,24(7):906-909.
ZhangJianliang,QinQifeng,HuangXianghua,etal.ResearchonModelingandECUIn-the-loopSimulatiomforTwoStrokePiston-aeroEngine[J].ChinaMechanicalEngineering,2013,24(7):906-909.
[6]LennartLjung.BlackBoxModelfromInputOutputMeasurement[C]//IEEEInstrumentationandMeasurementTechnologyConference.Budapest,Hungary,2001:21-23.
[7]GeveM.APersonalViewoftheDevelopmentofSystemIdentification[J].IEEEControlSystemsMagazine,2006,26(6):93-105.
[8]周文祥,黃金泉,黃開明.航空發動機簡化實時模型仿真研究[J].南京航空航天大學學報,2005,37(2):251-255.
ZhouWenxiang,HuangJinquan,HuangKaiming.Real-timeSimulationSystemforAeroengineBasedonSimplifiedModel[J].JournalofNanjingUniversityofAeronautics&Astronautics,2005,37(2):251-255.
[9]潘慕絢,黃金泉.航空發動機模型參考自適應控制綜述[J].航空發動機,2003,29(2):51-54.
PanMuxuan,HuangJinquan.SummaryofModelReferenceAdaptiveControlofAeroengine[J].Aeroengine,2003,29(2):51-54.
[10]孫建國,黃金泉,葉志峰,等.現代航空動力裝置控制[M].北京:航空工業出版社,2009.
[11]于連棟,費業泰.狀態變量分析法在系統辨識中的應用[J].中國機械工程,2004,15(16):1472-1474.
YuLiandong,FeiYetai.ApplicationofAnalysisMethodofStateVariableinSystemIdentification[J].ChinaMechanicalEngineering,2004,15(16):1472-1474.
[12]倪博溢,蕭德云.MATLAB環境下的系統辨識仿真工具箱[J].系統仿真學報,2006,18(6):1493-1496.
NiBoyi,XiaoDeyun.SystemIdentificationandSimulationToolboxunderMATLABEnvironment[J].JournalofSystemSimulation,2006,18(6):1493-1496.
[13]廉筱純,吳虎.航空發動機原理[M].西安:西北工業大學出版社,2005.
(編輯張洋)
Research on MTE Real-time Modeling Based on Dynamic Coefficient Method
Xu XinZhang TianhongSheng Hanlin
Jiangsu Province Key Laboratory of Aerospace Power Systems,Nanjing University of Aeronautics and Astronautics,Nanjing,210016
This paper obtained a series of rotating speed-fuel consumption steady state and dynamic property of the engine at some steady points by using system identification method of time domain, obtained steady state relationship and acceleration coefficient for full range by using interpolation method, and established real-time model of the engine for full range by using dynamic coefficient method.This model was characterized by simple structure,small calculating amount,high real-time control.Simulation results show that this model can well reflect the steady state and dynamic property of MTE,compared to experimental data, steady point’s deviation of the model is less than 1%,deviation of transient process is less than 6%,which can apply to fault-tolerant control of MTE.
micro-turbojet engine(MTE);fault tolerant control;system identification;dynamic coefficient method;real-time model
2013-10-10
國家自然科學基金資助項目(51176075);江蘇高校優勢學科建設工程資助項目
V233.7DOI:10.3969/j.issn.1004-132X.2015.02.021
徐鑫,男,1989年生。南京航空航天大學能源與動力學院碩士研究生。主要研究方向為微型渦噴發動機控制器設計與容錯控制。張天宏,男,1968年生。南京航空航天大學能源與動力學院教授。盛漢霖,男,1986年生。南京航空航天大學能源與動力學院博士研究生。

