多目標置換流水車間調度的改進食物鏈算法
陳可嘉 周曉敏
福州大學,福州,350108
多目標置換流水車間調度的改進食物鏈算法
陳可嘉周曉敏
福州大學,福州,350108
針對目標函數為最小化最大完成時間和總延遲時間的多目標置換流水車間調度問題,提出了一種改進的食物鏈算法。該算法在食物鏈算法的基礎上,引入基于Pareto最優解的快速非支配性排序和個體擁擠距離計算,增強了算法的尋優性能。對OR-Library三個典型算例的優化比較表明,該算法在解的質量上明顯超越NSGA-Ⅱ算法。
置換流水車間調度;多目標優化;食物鏈算法;Pareto最優解
0 引言
流水車間調度問題作為許多實際流水線生產調度的簡化模型,是生產調度中的一個重要研究對象。在實際生產中,生產者追求的目標并不是單一的,往往要求生產能夠滿足多個目標。因此,多目標流水車間調度問題更加符合生產制造的實際情況,具有研究的現實意義。Ishibuchi等[1]提出了基于局部搜索的遺傳算法,求解了以最小化最大完成時間和最大延遲時間為目標的流水車間調度問題。Ravindran等[2]分析了最小化最大完成時間和最小化總流程時間的雙目標流水車間調度問題,設計了三種啟發式算法。Yagmahan等[3]采用蟻群算法,解決了以最小化最大完成時間和總流程時間為目標的流水車間調度問題。Lee等[4]針對目標函數為最小化加權延遲時間和最大完成時間的流水車間調度問題,給出了遺傳算法。多目標置換流水車間調度要求每臺機器上工件加工順序相同,是一類典型多目標流水車間調度問題,受到了眾多研究學者的關注。Pasupathy等[5]研究了以最小化最大完成時間和總流程時間為目標的置換流水車間調度問題,提出了基于Pareto最優解的遺傳算法。Lemesre等[6]應用精確并行方法,解決了目標函數為最小化最大完成時間和總延遲時間的置換流水車間調度問題。Qian等[7]探討了具有有限緩沖區的同時最小化最大完成時間和最大延遲時間的多目標置換流水車間調度問題,給出了混合差分進化算法。Dubois-Lacoste等[8]將最大完成時間、總完成時間、無加權總延遲時間、加權總延遲時間組合成五類雙目標置換流水車間調度問題,設計了基于兩階段局部搜索和Pareto局部搜索的混合算法。Arroyo等[9]針對最小化最大完成時間、最大延遲時間、總流程時間的多目標置換流水車間調度問題,提出了基于貪婪隨機自適應搜索的啟發式算法。不難看出,智能算法已逐漸成為求解多目標流水車間調度問題的重要工具,對于智能算法的探索加快了復雜多目標置換流水車間調度問題的求解,使得結果更加貼近實際需求。
近年來,國內學者對多目標置換流水車間調度問題的關注也越來越多。楊開兵等[10]將遺傳算法與局部搜索相結合,求解了帶調整時間的以最小化最大完成時間和最大延遲時間為目標的置換流水車間調度問題。董興業等[11]針對最小化最大完成時間和總流程時間的多目標置換流水車間調度問題,給出了局部搜索算法。秦艷[12]采用改進交叉策略的遺傳算法,解決了加權形式的多目標置換流水車間調度問題。顯然,國內學者在研究多目標置換流水車間調度問題時,注重對現有算法進行改進,從而完善算法性能,提高算法精度。
食物鏈算法是模擬生態系統中食物鏈現象而提出的一種新型人工生命算法,具有魯棒性強、并行處理容易等優點,已在供應鏈計劃[13]、分銷網絡優化[14]等問題中取得了良好的應用效果。食物鏈與流水車間之間具有鏈式結構相似性,食物鏈算法對于多目標置換流水車間調度優化問題有著獨特的優勢。然而,從國內外已有文獻來看,將食物鏈算法應用于流水車間調度問題的研究相對較少,將食物鏈算法與多目標置換流水車間問題相結合的研究更少。基于此,本文設計了多目標置換流水車間調度的改進食物鏈算法,通過算例分析,驗證了算法的有效性。
1 問題描述
1.1多目標優化問題
假設求解多目標最小化問題,多目標優化問題的數學形式可描述為[15]
(1)
其中,x為決策向量,y為目標向量,X為決策向量x形成的決策空間,Y為目標向量y形成的目標空間。F()為將x映射至目標向量空間的優化函數,gi(x)≤0(i=1,2,…,h)為x需要滿足的h個約束條件。
定義1Pareto支配。設Xf為多目標優化問題的可行解集,F(x)={f1(x),f2(x),…,fk(x)}為目標向量,xk∈Xf,xl∈Xf,則稱xkPareto支配xl(簡稱支配,記作xkxl)。當且僅當下式成立時,xkPareto支配xl:
(2)
定義2Pareto最優解。如果在某一集合中不存在其他解x′Pareto支配x,則稱x為該集合中的Pareto非支配解(簡稱非支配解);如果x為多目標優化問題整個可行解集中的Pareto非支配解,則稱x為該問題的Pareto最優解。
定義3Pareto最優前沿。一個多目標優化問題所有的Pareto最優解對應的目標向量集合,構成了該問題的Pareto最優前沿。
1.2多目標置換流水車間調度問題
流水車間調度問題是研究m臺機器上n個工件的流水加工過程,每個工件以相同順序依次經過各臺機器的加工,同時約定每個工件在每臺機器上只加工一次,每臺機器一次在某一時刻只能夠加工一個工件,各個工件在各臺機器上所需的加工時間已知。進一步,若約定每臺機器上各個工件的加工順序相同,則稱其為置換流水車間調度問題。
本文多目標置換流水車間調度問題的優化目標是:確定各個工件在每臺機器上的最優加工順序,使得最大完成時間以及總延遲時間達到最小,最大完成時間越小意味著機器的利用率越高,總延遲時間越小意味著所有工件滿足交貨期的總體情況越好。
對于多目標置換流水車間調度問題有如下的數學模型:
(3)
s.t.C(1,1)=t(1,1)
(4)
C(1,j)=C(1,j-1)+t(1,j)
j=2,3,…,m
(5)
C(i,1)=C(i-1,1)+t(i,1)
i=2,3,…,n
(6)
C(i,j)=max{C(i-1,j);C(i,j-1)}+t(i,j)
(7)
i=2,3,…,n;j=2,3,…,m
Ci=C(i,m)=max{C(i-1,m);C(i,m-1)}+t(i,m)i=2,3,…,n
(8)
Cmax=C(n,m)
(9)
ti=max{0,Ci-di}i=1,2,…,n;j=1,2,…,m
(10)
s(i,j)+t(i,j)≤s(i+1,j)i=1,2,…,n;j=1,2,…,m
(11)
s(i,j)+t(i,j)≤s(i,j+1)i=1,2,…n;j=1,2,…,m
(12)
s(i,j)+t(i,j)=C(i,j)i=1,2,…n;j=1,2,…,m
(13)
s(i,j)≥0,C(i,j)≥0i=1,2,…n;j=1,2,…,m
(14)
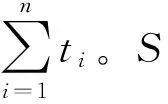
式(4)~式(9)表示最大完成時間Cmax的計算過程;式(10)表示工件Ji的延遲時間等于工件Ji完成時間和交貨期的差值與零之間的較大者;式(11)表示在某一時刻,機器Mj上最多只能加工一個工件;式(12)表示所有工件的工藝路線均相同;式(13)表示工件Ji在機器Mj上結束加工時間等于該工件在機器Mj上開始加工時間加上加工時間;式(14)為非負約束。
2 算法設計
2.1食物鏈算法介紹
食物鏈算法是根據生態系統中食物鏈這一重要的生態現象,借鑒行為生態學理論,利用具有一定自主推理且自主決策、能夠與環境動態交互的人工生命來仿真食物鏈物種之間的捕食行為和進化特征,所構造的一類具有食物鏈形式的人工生命算法。食物鏈算法的基本步驟如下[13-14]:
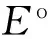
清華大學老校長梅貽琦說過,“大學之謂,非大樓也”。現在大學房子越蓋越豪華,但是教授越來越不像教授,學生越來越不像學生,大學精神不斷淪落,大學校園彌漫的學術不端氛圍,令人憂慮。高校、科研機構擔負著傳承文化、弘揚正義的職責。如果為人師表者學術道德失守,不僅有辱學術尊嚴,還會誤導學生、搞壞學術風氣。韓愈說,“師者,傳道、授業、解惑也”。教師除了教給學生學問外,更有義務教給他們做人的道理、做學問的道德。如果教師自身學術不端,即使道貌岸然給學生講學術道德,學生也聽不進去。
(2)覓食。人工生命個體在鄰域范圍內進行覓食,尋找最優的食物資源。若找到,則設當前最優食物資源位置為局部最優解,并增加能量Ee。若當前局部最優解優于歷史全局最優解,則更新全局最優解。若沒有找到,則消耗能量Ep。所有人工生命個體都要完成一次覓食搜索。
(3)位置更新。所有人工生命個體移動到當前最優食物資源位置。
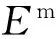
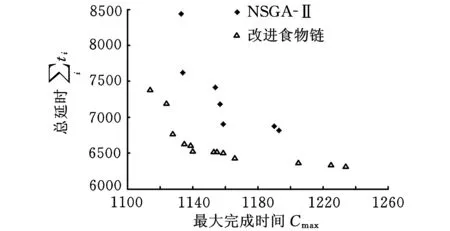
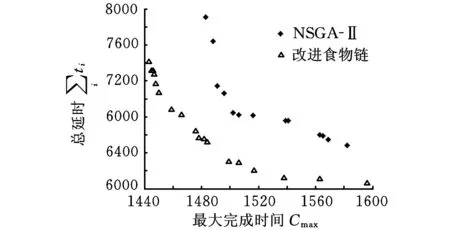
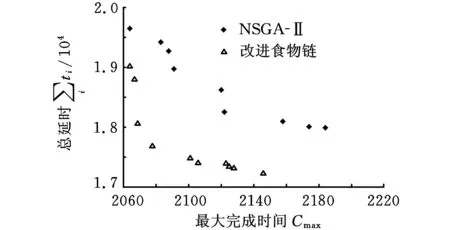
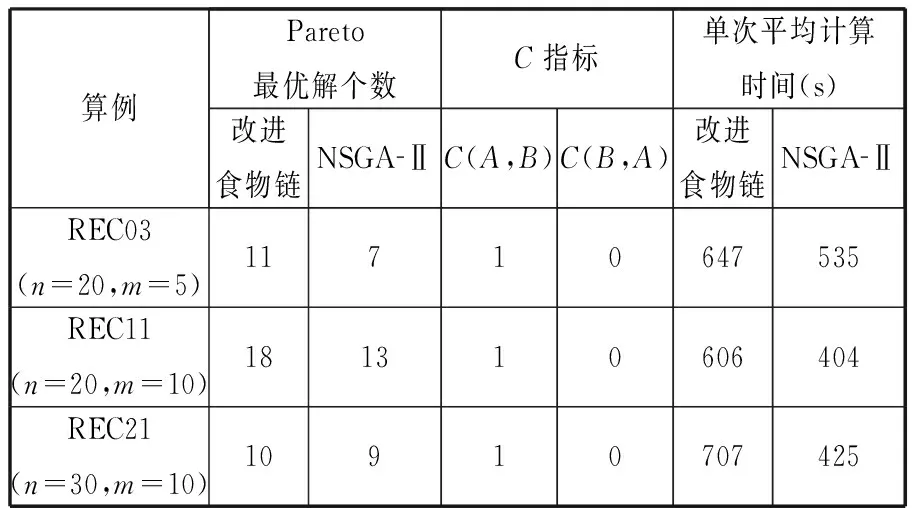
(5)循環控制。每完成一次人工生命集的新陳代謝,迭代次數K增加1。若迭代次數K 2.2改進食物鏈算法設計 多目標優化問題的傳統處理方法是給各個目標附加權重,將多目標轉化為單目標優化問題,從而求得唯一最優解。然而在實際多目標優化問題中,各個目標之間往往是相互制約、相互沖突的,同時決策者對于權重系數的選擇存在主觀因素,因此求解出多目標優化問題的Pareto最優解集,更加有利于決策者制定正確的決策。NSGA-Ⅱ是公認的最為有效的多目標進化算法之一[16],它對NSGA進行了改進,采用快速非支配排序,將種群中的個體進行分層,降低了計算的復雜性;通過計算個體的擁擠距離,判斷個體的分布是否均勻,提高了Pareto最優解的分布性。基于以上優點,本文引入NSGA-Ⅱ的快速非支配排序和個體擁擠距離計算,改進食物鏈算法,用于求解多目標置換流水車間調度問題。改進食物鏈算法的流程圖如圖1所示,具體計算步驟如下: 圖1 改進食物鏈算法流程圖 (1)初始化。定義N個人工生命個體,構成初始人工生命集。人工生命個體包括3個部分:第一部分采用基于工序的編碼方法,n個元素是n個工件號隨機排序形成的可行解;第二部分的2個元素為根據該可行解計算出的2個目標函數值;第三部分的2個元素分別是根據第二部分函數值進行快速非支配排序得到的個體等級數以及計算得到的個體擁擠距離,在初始化階段,該部分為空,在新陳代謝階段,該部分將被計算。例如,對于工件數量n=4、機器數量m=3的置換流水車間調度問題,加工時間矩陣t和交貨期矩陣d(本文加工時間和交貨期均為量綱一參量)為 (2)覓食。在算法的覓食階段,對人工生命個體中第一部分的元素排序進行調整,并重新計算第二部分的目標函數值。本文采用可變鄰域實現覓食,通過可變鄰域,使得覓食的方向多樣化,提高覓食的遍歷性。可變鄰域設置為δ=δinitial-mod(K,10)×(δinitial/10),其中,δinitial為初始鄰域,mod(K,10)為求K/10的余數。為了保證至少調整兩個元素,通過計算max(2,δn),確定人工生命個體中需要調整的元素個數。對于步驟(1)所生成的人工生命個體Gk1,假設δinitial=0.5,K=6,因此δ=0.2,max(2,δn)=2。隨機選出2個元素,假設為元素“4”和元素“1”,對這兩個元素隨機排序,得到新人工生命個體Gk2:(1-3-4-2)-(32-14)-(null-null)。對新個體和原個體進行非支配排序,可以看出,新個體的兩個目標函數值都比原個體的兩個目標函數值小,新個體支配原個體,此次覓食成功,個體更新。若新個體的兩個目標函數值,一個比原個體大,一個比原個體小,則這兩個個體處于同一非支配等級上,個體不更新;若新個體的兩個目標函數值都比原個體要大,原個體支配新個體,個體也不更新;對于這兩種情況,原個體沒有覓食成功。 (3)位置更新。當人工生命集中所有人工生命個體且完成覓食行為后,形成一個新的人工生命集,其中的人工生命個體實現了位置的優化和更新。 (4)新陳代謝。在算法的新陳代謝階段,選取成熟的人工生命個體繁殖產生下一代新的人工生命個體,以彌補死亡的人工生命個體,使人工生命集中的個體數量保持不變。在選擇成熟人工生命個體時,引入快速非支配排序及個體擁擠距離計算的方法,代替傳統的適應值計算比較,以便能夠更加有效地選出成熟人工生命個體。 非支配排序就是按照Pareto支配的定義,確定人工生命個體的非支配性。快速非支配排序,是將人工生命集中的人工生命個體按照非支配性進行分層,每一層人工生命個體的非支配性相同。具體過程為:首先,找出當前人工生命集中的所有非支配個體并分配等級1;然后,排除該層非支配個體集,對剩下的個體進行非支配個體集搜索并分配等級2;重復這個過程,直到人工生命集中的所有個體都被賦予相應的等級為止。 通過快速非支配排序及個體擁擠距離計算,實現人工生命個體第三部分等級數和擁擠距離2個元素的賦值,進而完成新陳代謝。對人工生命個體進行快速非支配排序,賦予等級數。將人工生命個體按照等級數從小到大排序,選取前N/2個人工生命個體,采用與覓食行為相同的策略,產生N/2個新人工生命個體。將N/2個新人工生命個體與原來N個人工生命個體混合,再次進行快速非支配排序,更新等級數。對同一非支配層中的人工生命個體,計算擁擠距離,將人工生命個體按照擁擠距離從大到小排序。通過非支配等級和擁擠距離的雙重排序,淘汰排序靠后的N/2個人工生命個體,保留前N個成熟人工生命個體形成新一代的人工生命集。例如,對于步驟(1)生成的Gk1和步驟(2)生成的Gk2,采用快速非支配排序對它們分配等級數,由于Gk2的兩個目標函數值都要小于Gk1,因此Gk2分配等級1、Gk1分配等級2。同時,由于Gk2優于Gk1,Gk2產生一個新人工生命個體Gk3:(2-1-3-4)-(33-21)-(null-null)。對Gk1、Gk2、Gk3三個人工生命個體再次進行快速非支配排序,Gk1和Gk2等級不變,Gk3分配等級2。假設三個人工生命個體的擁擠距離分別為0.6、0.7、∞,則Gk1:(4-3-1-2)-(36-15)-(2-0.6);Gk2:(1-3-4-2)-(32-14)-(1-0.7);Gk3:(2-1-3-4)-(33-21)-(2-∞)。因此三個人工生命個體的排序為:Gk2-Gk3-Gk1。按照新陳代謝原則,淘汰Gk1。 步驟(5)循環控制。通過以上步驟,人工生命集完成了一次循環過程,達到最大循環次數后,算法終止。非支配等級為1的所有個體就是算法找到的一組Pareto最優解。 3.1Pareto最優解比較指標 本文采用以下兩個指標對算法求得的Pareto最優解進行比較: (1)Pareto最優解的個數。通過將每種算法求得的Pareto最優解的個數進行比較,可以看出不同算法的搜索能力。個數越多,表明算法搜索能力越強。 (2)C指標。采用文獻[15]中的C指標評價兩種算法產生的Pareto最優解集A和B,C指標的計算公式: (15) C(A,B)表示B的Pareto最優解被A的Pareto最優解占優支配的個數占B的Pareto最優解總數的比率,它的取值介于0到1之間。當B中任何點都被A中某些點占優支配時,C(A,B)=1。當B中所有點都不被A中任何點占優支配時,C(A,B)=0。一般C(A,B)≠C(B,A)。該指標反映了解的質量及算法的收斂性。 3.2算例結果分析 以文獻[16]提出的NSGA-Ⅱ作為參照算法,它克服了NSGA的缺點,是目前公認的最為有效的多目標進化算法之一。設置兩種算法的群體規模均為200,最大迭代次數均為500,NSGA-Ⅱ的交叉概率和變異概率分別為0.9和0.1,改進食物鏈算法的初始鄰域為0.5。在Intel Core i3-2350M CPU 2.30 GHz處理器、2GB內存、Windows XP系統下,以MATLAB實現兩種算法,分別對三個典型算例運算15次,合并各次的解集,剔除其中的劣解,獲得三個典型算例最終的Pareto最優解集(圖2~圖4)。結果顯示,改進食物鏈算法比NSGA-Ⅱ能夠獲得更多的Pareto最優解,同時改進食物鏈算法產生的Pareto最優解均在NSGA-Ⅱ產生的解的左下方,得出的結果要優于NSGA-Ⅱ。 圖2 兩種算法優化REC03算例獲得的Pareto最優解集 圖3 兩種算法優化REC11算例獲得的Pareto最優解集 圖4 兩種算法優化REC21算例獲得的Pareto最優解集 將改進食物鏈算法與NSGA-Ⅱ兩種算法優化三個典型算例的求解統計結果列于表1。從表1可以看出,對于三個典型算例,改進食物鏈算法求得的Pareto最優解個數均多于NSGA-Ⅱ。C指標結果更進一步表明,改進食物鏈算法獲得的Pareto最優解集A與NSGA-Ⅱ獲得的Pareto最優解集B相比,在B中任意一個Pareto最優解,A中都存在優于它的解。就單次平均計算時間而言,改進食物鏈算法求解三個典型算例的時間均稍長于NSGA-Ⅱ。這主要是由于為了尋找更多的最優解,改進食物鏈算法在覓食階段對于Pareto最優解的局部搜索花費了較多時間。綜合以上結果可知,在相同的條件下,雖然改進食物鏈算法的優化時間略長于NSGA-Ⅱ,但是改進食物鏈算法對多目標置換流水車間調度問題的尋優能力明顯勝過NSGA-Ⅱ,從而驗證了改進食物鏈算法求解多目標置換流水車間調度問題的有效性。 表1 求解統計結果 多目標的置換流水車間調度問題更加符合實際的生產情況,具有重要的研究意義。本文根據流水車間與食物鏈具有相似鏈式結構的特點,提出了一種改進的食物鏈算法,并用于求解多目標置換流水車間調度問題。改進食物鏈算法采用可變鄰域覓食,保證了搜索方向的多樣性及遍歷性;引進快速非支配性排序和個體擁擠距離計算,提高了求解多目標問題的優化性能。應用改進食物鏈算法對OR-Library三個典型算例進行求解,研究結果表明,本文給出的算法取得了比NSGA-Ⅱ更加理想的Pareto最優解集,具有較好的實際應用前景。 [1]Ishibuchi H, Murata T. A Multi-objective Genetic Local Search Algorithm and Its Application to Flowshop Scheduling[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C: Applications and Reviews, 1998, 28(3): 392-403. [2]Ravindran D, Haq A N, Selvakumar S J, et al. Flow Shop Scheduling with Multiple Objective of Minimizing Makespan and Total Flow Time[J]. International Journal of Advanced Manufacturing Technology, 2005, 25(9/10): 1007-1012. [3]Yagmahan B, Yenisey M M. A Multi-objective Ant Colony System Algorithm for Flow Shop Scheduling Problem[J]. Expert Systems with Applications, 2010, 37(2): 1361-1368. [4]Lee C K M, Lin D, Ho W, et al. Design of a Genetic Algorithm for Bi-objective Flow Shop Scheduling Problems with Re-entrant Jobs[J]. International Journal of Advanced Manufacturing Technology, 2011, 56(9/12): 1105-1113. [5]Pasupathy T, Rajendran C, Suresh R K. A Multi-objective Genetic Algorithm for Scheduling in Flow Shops to Minimize the Makespan and Total Flow Time of Jobs[J]. International Journal of Advanced Manufacturing Technology, 2006, 27(7/8): 804-815. [6]Lemesre J, Dhaenens C, Talbi E G. An Exact Parallel Method for a Bi-objective Permutation Flowshop Problem[J]. European Journal of Operational Research, 2007, 177(3): 1641-1655. [7]Qian B, Wang L, Huang D X, et al. An Effective Hybrid DE-based Algorithm for Multi-objective Flow Shop Scheduling with Limited Buffers[J]. Computers & Operations Research, 2009, 36(1): 209-233. [8]Dubois-Lacoste J, López-Ibáez M, Stützle T. A Hybrid TP+PLS Algorithm for Bi-objective Flow-shop Scheduling Problems[J]. Computers & Operations Research, 2011, 38(8): 1219-1236. [9]Arroyo J E C, de Souza Pereira A A. A GRASP Heuristic for the Multi-objective Permutation Flowshop Scheduling Problem[J]. International Journal of Advanced Manufacturing Technology, 2011, 55(5/8): 741-753. [10]楊開兵, 劉曉冰. 帶調整時間的多目標流水車間調度的優化算法[J]. 工業工程與管理, 2008, 13(5): 1-5. Yang Kaibing, Liu Xiaobing. Optimization Algorithm for Multi-objective Flow Shop Scheduling with Setup Times[J]. Industrial Engineering and Management, 2008, 13(5): 1-5. [11]董興業, 黃厚寬, 陳萍. 多目標同順序流水作業的局部搜索算法[J]. 計算機集成制造系統, 2008, 14(3): 535-542. Dong Xingye, Huang Houkuan, Chen Ping. Local Search Algorithm for Multi-objective Permutation Flowshop Sequencing Problem[J]. Computer Integrated Manufacturing Systems, 2008, 14(3): 535-542. [12]秦艷. 改進交叉策略的GA在流水車間多目標調度中的應用[J]. 現代制造工程, 2010(12): 29-32. Qin Yan. Application of GA with Improved Crossover Operators in Multi-objective Flow Shop Scheduling[J]. Modern Manufacturing Engineering, 2010(12): 29-32.[13]喻海飛, 汪定偉. 食物鏈算法及其在供應鏈計劃中的應用[J]. 系統仿真學報, 2005, 17(5): 1195-1198. YuHaifei,WangDingwei.Food-chainAlgorithmandApplicationtoSupply-chainPlanning[J].JournalofSystemSimulation, 2005, 17(5): 1195-1198. [14]喻海飛, 汪定偉. 食物鏈算法及其在分銷網絡優化中的應用[J]. 東北大學學報(自然科學版), 2006, 27(2): 146-149. YuHaifei,WangDingwei.Food-chainAlgorithmandItsApplicationtoOptimizingDistributionNetwork[J].JournalofNortheasternUniversity(NaturalScience), 2006, 27(2): 146-149. [15]ZitzlerE.EvolutionaryAlgorithmsforMultiobjectiveOptimization:MethodsandApplications[M].Aachen:ShakerVerlag, 1999. [16]DebK,PratapA,AgarwalS,MeyarivanT.AFastandElitistMultiobjectiveGeneticAlgorithm:NSGA-Ⅱ[J].IEEETransactionsonEvolutionaryComputation, 2002, 6(2):182-197. [17]BeasleyJE.OR-Library[DB/OL]. (2012-06-12)[2013-09-13].http://people.brunel.ac.uk/~mastjjb/jeb/info.html. [18]師瑞峰, 周泓, 上官春霞. 混合遞進多目標進化算法及其在flowshop排序中的應用[J]. 系統工程理論與實踐, 2006, 26(8): 101-108. ShiRuifeng,ZhouHong,ShangguanChunxia.AHybridEscalatingMulti-objectiveEvolutionaryAlgorithmwithItsApplicationtoFlowShopProblems[J].SystemsEngineering-Theory&Practice, 2006, 26(8): 101-108. (編輯郭偉) Improved Food Chain Algorithm for Multi-objective Permutation Flow Shop Scheduling Chen KejiaZhou Xiaomin Fuzhou University,Fuzhou,350108 An improved food chain algorithm was proposed for permutation flow shop scheduling with multiple objectives of minimizing makespan and total tardiness. Fast non-dominated sorting and crowded distance estimation were introduced into the food chain algorithm to improve the optimization ability based on Pareto optimal solutions. Three typical OR-Library examples were selected to conduct comparison. Numerical results show that the designed algorithm can obtain much better solutions than NSGA-Ⅱ. permutation flow shop scheduling; multi-objective optimization; food chain algorithm; Pareto optimal solution 2013-11-08 國家自然科學基金資助項目(70901021,71201033);教育部新世紀優秀人才支持計劃資助項目(NCET-11-0903) F406.2DOI:10.3969/j.issn.1004-132X.2015.03.011 陳可嘉,男,1978年生。福州大學經濟與管理學院教授、博士。主要研究方向工業工程、系統工程。周曉敏,女,1988年生。福州大學經濟與管理學院碩士研究生。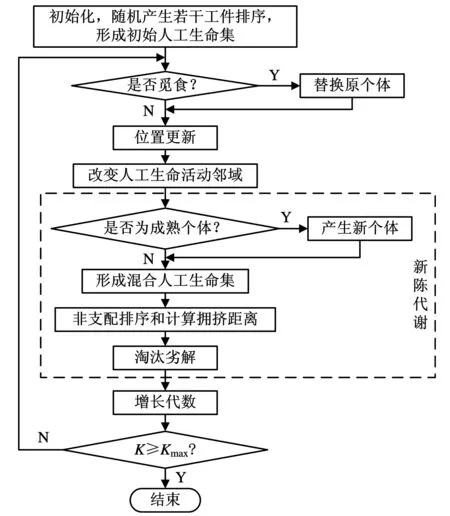
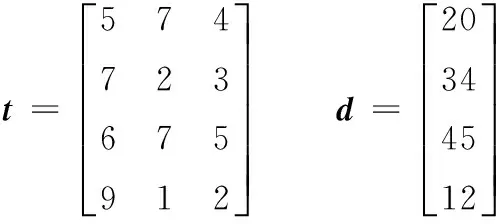
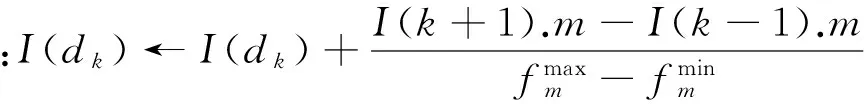
3 算例分析
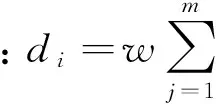
4 結語

