串聯結構產品可靠性建模與統計分析
陳曉平 陳文華 許家清 胡如夫
1.浙江理工大學機電產品可靠性技術研究浙江省重點實驗室,杭州,3100182.寧波工程學院,寧波,315016
串聯結構產品可靠性建模與統計分析
陳曉平1,2陳文華1許家清2胡如夫2
1.浙江理工大學機電產品可靠性技術研究浙江省重點實驗室,杭州,3100182.寧波工程學院,寧波,315016
針對電連接器接觸對數量較小的情況下,其接觸壽命不適宜用Weibull分布描述的問題,研究了串聯結構產品可靠性建模及統計分析方法,建立了任意接觸對數量下電連接器接觸壽命分布的可靠性模型,研究了基于區間數據的模型參數點估計和Bootstrap區間估計方法。試驗研究結果表明:對于串聯結構產品,采用串聯結構的真實分布比近似地采用威布爾分布的擬合優度高,可更加客觀地評價產品的可靠性水平。
電連接器;串聯系統;可靠性模型;統計分析
0 引言
串聯結構是一種常見的產品結構類型,對于串聯結構產品,只有構成產品的所有單元都能正常地執行其功能時才能保證整個系統有效地運行。一個復雜的航天器系統分布著上千個各種類型的電連接器,只要有一個電連接器發生失效,就有可能導致整個系統發射任務的失敗[1]。電連接器是由一定數量的接觸對組成的,只要一個接觸對發生失效,就會造成電連接器整體的失效,因此,通常將電連接器接觸可靠性問題按串聯結構進行研究[2-4]。目前,已有的研究通常是將電連接器接觸壽命近似地按二參數Weibull分布來進行的[5-14],而Weibull分布近似方法只有在電連接器接觸對數量足夠多時理論上才近似可行[15],而常用電連接器接觸對一般數量不多,只有幾個或十幾個,如Y11X-0804型電連接器只有4個接觸對,因此,有必要研究串聯結構產品可靠性建模與統計分析的方法,以便對串聯結構產品的可靠性做出一個正確評價。本文以Y11X-1419型電連接器為實例,研究串聯結構產品壽命的概率分布,以及相應的統計分析方法。
1 串聯結構產品可靠性統計模型
某串聯結構產品由m個相同的單元組成,各個單元的失效時間分別為t1,t2,…,tm,它們相互獨立,ti(i=1,2,…,m)的分布密度函數為f(t,θ)(θ是分布參數),分布函數為F(t,θ),則該串聯結構產品的壽命分布相當于求最小次序統計量t(1)的分布,即
Ft(1)(t,θ)=1-(1-F(t,θ))m
相應的概率密度函數為
ft(1)(t,θ)=m(1-F(t,θ))m-1f(t,θ)
以電連接器為例,假定接觸對數量為m,其中第i個接觸對的壽命為ti(i=1,2,…,m),接觸對的壽命相互獨立,均服從對數正態分布[3]。電連接器可視為一個接觸對相互獨立的串聯系統,其接觸壽命T由最早失效的接觸對決定,即T=min{t1,t2,…,tm},因此,電連接器的接觸壽命分布F(t)可由下式來確定[3]:
F(t)=1-P{T>t}=1-(1-Fx(t))m
(1)
其中,Fx(t)為單個接觸對的壽命分布,有
(2)
式中,μ為對數壽命均值;σ為對數壽命標準差。
因而,有
(3)
電連接器接觸壽命的概率密度函數為
(4)
2 模型參數的估計方法
2.1模型參數點估計
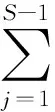
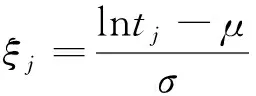
(5)
式中,Φ(·)為標準正態分布的分布函數。
對式(5)取對數,可得
(6)
其中,F(t0)=0。解似然函數方程組
(7)
式中,φ(·)為標準正態分布的密度函數。
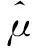
2.2模型參數Bootstrap區間估計
2.2.1Bootstrap區間估計方法
Bootstrap方法是Efron等[9-10]提出的一種統計模擬方法,本質上是一種再抽樣技術,即把樣本看作是總體的一個“縮影”,其基本思想是[11]:既然經驗分布函數是總體分布的良好擬合,那么來自總體分布的隨機觀測值的概率性質可以用經驗分布函數的相應統計量的概率性質來近似刻畫,而后者可以通過計算機模擬甚至直接計算得到。
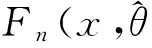
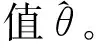
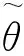
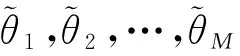
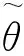
2.2.2Bootstrap糾偏估計
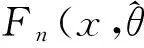
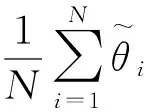
3 實例分析
3.1擬合優度檢驗
Y11X-1419型電連接器由m=19個接觸對組成,選取樣本量n=20進行壽命試驗,溫度應力水平為105℃,試驗的截尾時間為tS=1500 h。定時測試的時間節點、各測試區間的失效數如表1所示[16],有5個樣本到達截尾時間沒有失效。

表1 各測試區間的失效數
擬合優度的檢驗,可以根據樣本的測量值,檢驗其母體的分布與假設的理論分布相一致的程度來衡量[15]。擬合優度檢驗的方法很多,其中皮爾遜卡方檢驗應用最廣泛[17-19],其統計量為
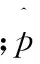
對于上述實例,區間數k=7,未知參數個數r=2,按電連接器接觸壽命真實分布計算,可得到檢驗統計量χ2=3.578。在顯著性水平α=0.05下,由于P(χ2(k-r-1)<3.578)=0.4561>α,假設不能拒絕,于是通過真實分布擬合檢驗。
若將電連接器接觸壽命近似為Weibull分布,則其檢驗統計量χ2=555.078。在顯著性水平α=0.05下,P(χ2(k-r-1)<555.078)≈0<α,假設不能成立,于是Weibull布擬合檢驗不能通過。
結果表明:相對于近似Weibull分布,采用串聯結構的真實分布能更準確地描述產品的壽命分布。
3.2參數估計
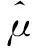
相應地,可靠度函數為
3.3估計精度檢驗
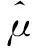
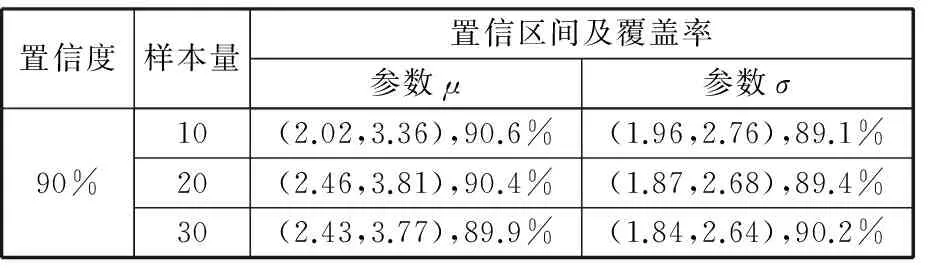
表2 不同樣本量下的Bootstrap置信區間精度模擬結果
從模擬結果看,在各置信水平和各樣本容量下,用Bootstrap方法求得的置信區間的估計值覆蓋率都基本達到置信水平的要求,表明本文所提出的模型參數估計方法是可行的。
4 結束語
本文在建立串聯結構產品可靠性模型的基礎上,研究了基于區間試驗數據的模型參數點估計方法,同時研究了通過Bootstrap區間估計和糾偏處理求解小樣本條件下模型參數和特征量的置信區間估計的方法。研究表明:對于串聯結構產品,采用串聯結構的真實分布比近似Weibull分布擬合效果好,可更加客觀地評價產品的可靠性水平。
[1]邱利瓊,舒俊輝.串聯系統可靠性模糊優化[J].重慶大學學報,2002,25(7):20-22.
Qiu Liqiong,Shu Junhui.Fuzzy Optimization for Reliability Apportionment of Series System[J].Journal of Chongqing University(Natural Sciecne Edition),2002,25(7):20-22.
[2]高亮,陳文華,劉娟,等.航天電連接器的空間環境效應和失效模式分析[J].中國機械工程,2010,21(13):1598-1604.
Gao Liang,Chen Wenhua,Liu Juan,et al.Analysis of Space Environment Effects and Failure Modes of Aerospace Electrical Connectors[J].China Mechanical Engineering,2010,21(13):1598-1604.
[3]陳文華,程耀東,李平真,等.航天電連接器的可靠性數學模型[J].航空學報,1997,18(6):732-734.
Chen Wenhua,Cheng Yaodong,Li Pingzhen,et al.Reliability Mathematics Model of Aerospace Electrical Connector[J].Acta Aeronautica Et Astronautica Sinica,1997,18(6):732-734.
[4]潘駿.航天電連接器振動可靠性建模與評估[D].杭州:浙江大學,2002.
[5]陳文華,楊帆,劉俊俊,等.航天電連接器的可靠性統計通用模型[J]. 機械工程學報,2012,48(22):177-181,188.
Chen Wenhua,Yang Fan,Liu Junjun,et al.Theory and Method for Simulation Evaluation of Accelerated Life Test Plan under Step-stress[J].Journal of Mechanical Engineering,2012,48(22):177-181,188.
[6]錢萍,陳文華,馬子魁,等.綜合應力加速壽命模型驗證方法的研究[J].機械工程學報,2010,46(24):156-161.
Qian Ping,Chen Wenhua,Ma Zikui,et al.Research of Multiple Stresses Accelerated Life Model Verification Method[J].Journal of Mechanical Engineering,2010,46(24):156-161.
[7]錢萍,陳文華,高亮,等. 航天電連接器綜合應力可靠性統計模型的驗證[J].中國機械工程,2011,22(3):257-261,273.
Qian P, Chen W H,Gao L,et al.Reliability Statistical Model Verification of Aerospace Electrical Connectors under Multiple Stresses[J].China Mechanical Engineering,2011,22(3):257-261,273.
[8]Karl V,Bury K.Statistical Models in Applied Science[M].New York:John Wiley & Sons,1975.
[9]Efron B,Tibshirani R.An Introduction to the Bootstrap[M].London:Chapman & Hall,1993.
[10]Efron B.Better Bootstrap Confidence Intervals[J].Journal of American Statistical Association,1987(82):171-185.
[11]趙宇,楊軍,馬小兵.可靠性數據分析教程[M].北京:北京航空航天大學出版社,2009.
[12]Efron B.Bootstrap Methods[J].The Annuals of Statistics,1979,7(1):1-26.
[13]陳文華,李奇志,張為鄂.產品可靠性的bootstrap區間估計方法[J].機械工程學報,2003,39(6):106-109.
Chen Wenhua,Li Qizhi,Zhang,Weie.Method of Bootstrap Interval Estimation for Product Reliability[J].Chinese Journal of Mechanical Engineering,2003,39(6):106-109.
[14]普雷斯 W H,弗拉內里 B P,托科爾斯基 S A.數值方法大全[M].王璞,等譯.蘭州:蘭州大學出版社,1991.
[15]張杰,王海清,李玉明,等.基于主觀估計法和FMEDA的失效數據分析及應用[J].計算機工程與應用,2013,49(16):255-259.
Zhang Jie,Wang Haiqing,Li Yuming,et al.Failure Data Analysis Based on Subjective Estimation and FMEDA and Application[J].Computer Engineering and Applications,2013,49(16):255-259.
[16]陳文華.航天電連接器可靠性試驗和分析的研究[D].杭州:浙江大學,1997.
[17]Rausand M.System Reliability Theory:Models,Statistical Methods,and Applications[M].北京:國防工業出版社,2010.
[18]莊楚強,何春雄.應用數理統計基礎[M].廣州:華南理工大學出版社,2006.
[19]賈希勝.以可靠性為中心的維修決策模型[M].北京:國防工業出版社,2001.
(編輯郭偉)
Reliability Modeling and Statistical Analysis for Series Structural Products
Chen Xiaoping1,2Chen Wenhua1Xu Jiaqing2Hu Rufu2
1.Zhejiang Province’s Key Laboratory for Reliability Technology of Mechanical &Electrical Products,Zhejiang Sci-Tech University,Hangzhou,310018 2.Ningbo University of Technology,Ningbo,Zhejiang,315016
Due to the small number of electrical connector, the contact reliability life could not be described by the Weibull distribution model.This paper studied a new reliability modeling and statistical method, as well as the model parameter point estimation and Bootstrap interval estimation method for the reliability life analysis of any given numbers of electrical connector.The results were verified by the experiments and show that the real distribution may evaluate more accurately than Weibull distribution approximation model for the series structural products.
electrical connector;series system;reliability modeling;statistical analysis
2014-11-10
國家自然科學基金資助項目(51275480,51305215);全國統計科學研究計劃資助項目(2012LY061)
TH112DOI:10.3969/j.issn.1004-132X.2015.12.007
陳曉平,男,1978年生。浙江理工大學機電產品可靠性技術研究浙江省重點實驗室博士后研究人員,寧波工程學院機械工程學院副教授。主要研究方向為疲勞強度可靠性設計與試驗。陳文華(通信作者),男,1963年生。浙江理工大學機電產品可靠性技術研究浙江省重點實驗室教授、博士研究生導師。許家清,男,1965年生。寧波工程學院機械工程學院高級統計師。胡如夫,男,1966年生。寧波工程學院機械工程學院教授、博士。

