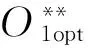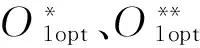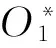浮動平底推桿-盤形凸輪組合機構的第Ⅰ類機構綜合問題
常 勇 林榮富 李延平
集美大學,廈門,361021
浮動平底推桿-盤形凸輪組合機構的第Ⅰ類機構綜合問題
常勇林榮富李延平
集美大學,廈門,361021
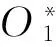
等距/網格/離散化;浮動坐標系;支撐函數;瞬時區域套;經濟搜索區域;脊點/脊線
0 引言
2010~2012年,筆者以德國進口的高速印刷機機構為研究對象,提出浮動滾子推桿-盤形凸輪組合機構的Ⅰ、Ⅱ兩類機構綜合問題,對后者通過引入“瞬時、整程區間(域)套”、“浮動數軸、坐標系”、“最經濟搜索帶域”等一系列概念和“降維快速求解”的理論方法,取得了較系統的研究成果[1-3]。回過頭來看,關于Ⅰ類機構綜合問題,早在1991年即通過引入“虛擬擺桿”的新概念得到較為圓滿的解決[4]。
隨著研究的自然引伸和拓展,筆者又產生了如下設想:若將前述機構中的滾子以平底替代,對應的Ⅰ、Ⅱ兩類機構綜合問題的準確描述該如何給出?如何解決?
平底較之滾子,在承載能力、潤滑特性、工作壽命、傳動和高速性能等諸多方面具有顯著優越性,自然也可以應用于高速印刷機機構場合。不難推想,研究解決上述引伸拓展性課題,具有機構學理論研究和工程實際應用兩方面的重要意義。
2013年,我們在進行Ⅱ類綜合問題準確描述的基礎上,通過揭示出“瞬時一維直線區域”和“瞬時區間套”,提出求解平底方位線容許選擇區域、凸輪基圓半徑許用取值范圍的基本原理等,解決了浮動平底推桿-盤形凸輪組合機構的第Ⅱ類機構綜合問題[5]。
國內外已有許多學者以壓力角為評價指標對平面盤形凸輪機構進行了尺寸綜合[6-10],對做平面運動的滾子從動件凸輪機構的綜合問題也作了相應研究[11-16]。
研究認為,浮動平底推桿-盤形凸輪組合機構Ⅰ類綜合問題的準確描述如下:已知從動構件系統的運動學尺寸、輸出件推/回程始終位置和(角)位移規律,推/回程許用壓力角、平底位于連桿位置及與連桿夾角等條件,求解凸輪軸心許用區域、凸輪基圓半徑r0許用取值范圍等。
較之平底Ⅱ類、滾子Ⅰ類機構綜合問題,平底Ⅰ類機構綜合問題困難、復雜得多。滾子情形時,因任一瞬時滾子中心確定,故根據虛擬擺桿概念和類速度圖原理,先求解任一瞬時凸輪軸心的位置區域,再通過求交得到整程凸輪軸心的位置區域,即可使綜合問題得到解決。然而平底情形時,雖然任一瞬時平底位置確定,但凸輪、平底接觸點即“瞬時滾子中心”不確定,導致任一瞬時的虛擬擺桿不確定,因此與類速度圖原理無法順利實現“鏈接”,從而導致“整程”凸輪軸心的位置區域無法求解確定。
與滾子情形“虛擬擺桿+類速度圖”的求解原理不同,本文提出一種新穎的“預設凸輪軸心O1+等距/網格/離散化+校核+取舍”的求解思路、原理和方法,較為圓滿地解決了浮動平底推桿-盤形凸輪組合機構的第Ⅰ類機構綜合問題。
圍繞“預設凸輪軸心O1+等距/網格/離散化+校核+取舍”的求解路線,通過建立“固定、浮動坐標系”,特別是通過引入“支撐函數法”、“瞬時區域套理論”、“經濟搜索區域”等新概念和“等距/網格/離散化”方法,循序漸進地研究了滿足ρ>0、α≤[α]∩α≤[α]r及ρ>0∩α≤[α]∩α≤[α]r(ρ為凸輪輪廓曲率半徑,α為壓力角,“∩”表示同時滿足)等單純、組合條件下凸輪軸心O1的求解原理、解析表達、“位置區域Πρ、Π[α]和Πρ∩[α]”及其形態特征,提出了搜索求解的思路、原理和方法,最后提出平底工作段及其長度、總長度的求解確定方法。
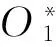
1 高速印刷機機構平底演化型第Ⅰ類機構綜合問題的準確表述
圖1所示為凸輪分別沿順時針、逆時針轉動的浮動平底推桿-盤形凸輪組合機構,由凸輪1、連桿2、搖塊3、搖桿4和機架0等組成,凸輪1、搖桿4分別為輸入件、輸出件。實質上,該機構可視為德國進口高速印刷機機構[1-3]的演化型式。
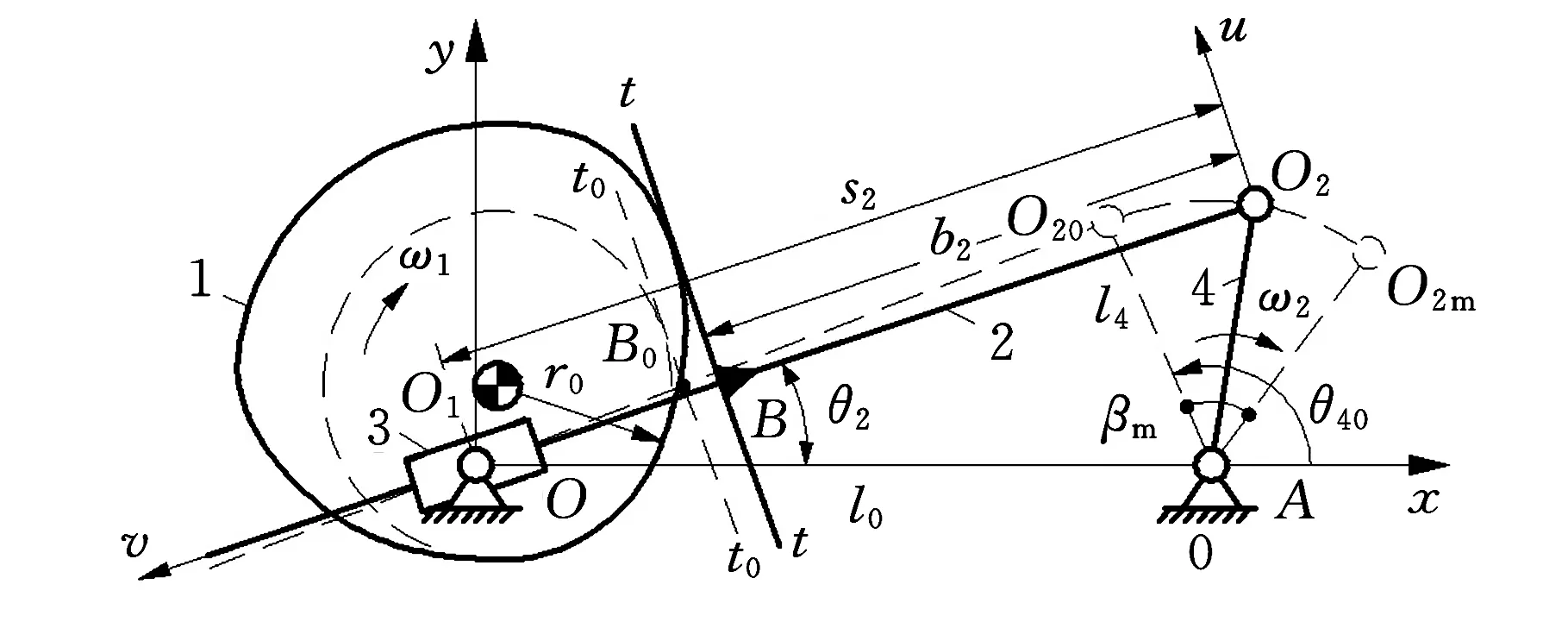
(a)凸輪順時針轉動
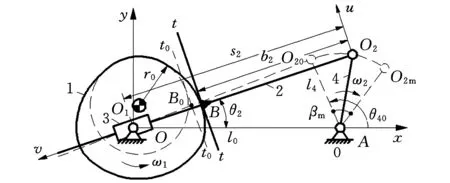
(b)凸輪逆時針轉動圖1 浮動平底推桿-盤形凸輪組合機構
圖1所示的兩機構的差異是凸輪分別沿順時針、逆時針轉動,其機構綜合問題準確描述如下:
已知:機架和搖桿長度分別為l0、l4,t-t垂直于OO2,OO2與t-t的交點為B,O2與t-t間的距離為b2,搖桿的初位角為θ40、行程角為βm,搖桿推/回程位移規律分別為β=β(θ1)、βr=βr(θ1),推/回程運動角分別為Φ、Φr,推/回程許用壓力角分別為[α]、[α]r。
求解:滿足ρ>0、α≤[α]∩α≤[α]r條件的機構解集,即凸輪軸心O1的容許選擇區域、凸輪基圓半徑r0的許用取值范圍等。
顯而易見,上述機構綜合問題屬于第Ⅰ類機構綜合問題。
2 預先準備工作
2.1固定坐標系建立和預備公式推導
建立固定直角坐標系Oxy,如圖1所示。選取搖塊軸心與原點O重合,x軸正向與OA方向一致,θ2、θ4分別為任一瞬時連桿、搖桿位置角,即OO2、AO2與x軸正向夾角,θ1為凸輪轉角。
建立封閉矢量方程(略),連桿2的時變長度(s2、s20)、位置角(θ2、θ20)和類角速度(dθ2/dθ1)分別為
(1)
(2)
θ2=arctan{l4sin(θ40-β)/[l0+l4cos(θ40-β)]}
(3)
θ20=arctan[l4sinθ40/(l0+l4cosθ40)]
(4)
(5)
(6)
式中,xO2、yO2為O2點的x、y坐標。
據上可知,s2、θ2、dθ2/dθ1和xO2、yO2等皆為θ1的一元函數。
連桿2的絕對瞬心P20的坐標為
(7)
連桿2的相對瞬心P21的坐標為
(8)
式(8)中,“±”中的“+”表示適用于凸輪順時針轉動的推程前半區段和凸輪逆時針轉動的推程后半區段,“-”則表示適用于凸輪順時針轉動的推程后半區段和凸輪逆時針轉動的推程前半區段。
如圖2所示,P21、P20兩點和P21、O1(P10)兩點間距離分別為
(9)
lP21P20、lP21O1皆是θ1的一元函數。下面將lP21P20簡記為l21。
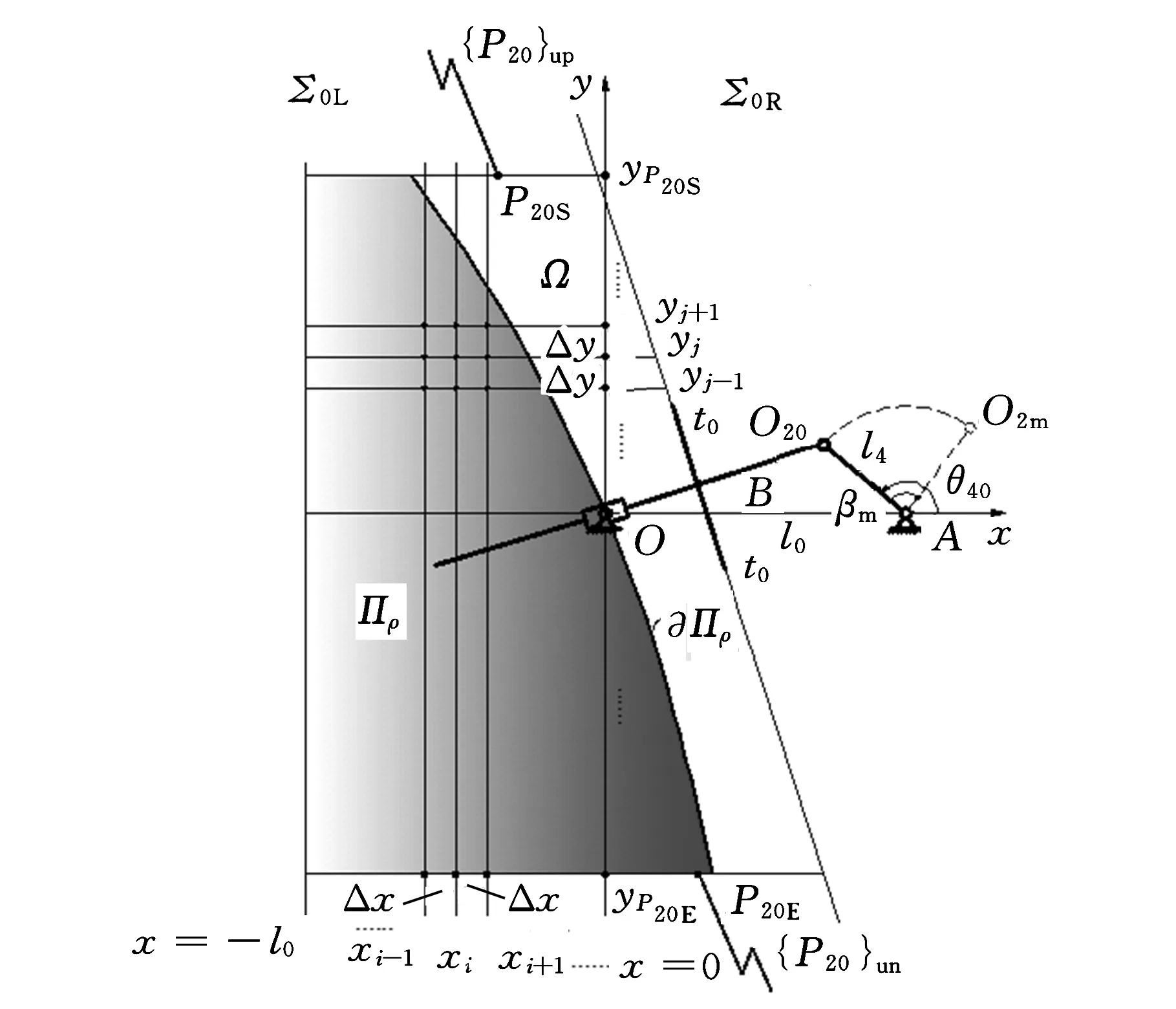
如圖1所示,點B的坐標為
(10)
點B0的坐標為
(11)
s20、θ20可據式(2)和式(4)解得。
任一瞬時,t-t的方程為
cotθ2x+y-cotθ2xB-yB=0
(12)
推程起始瞬時,t0-t0的方程為
cotθ20x+y-cotθ20xB0-yB0=0
(13)
點(xk,yk)至t0-t0的距離為
d=|cotθ20xk+yk-cotθ20xB0-yB0|sinθ20
(14)
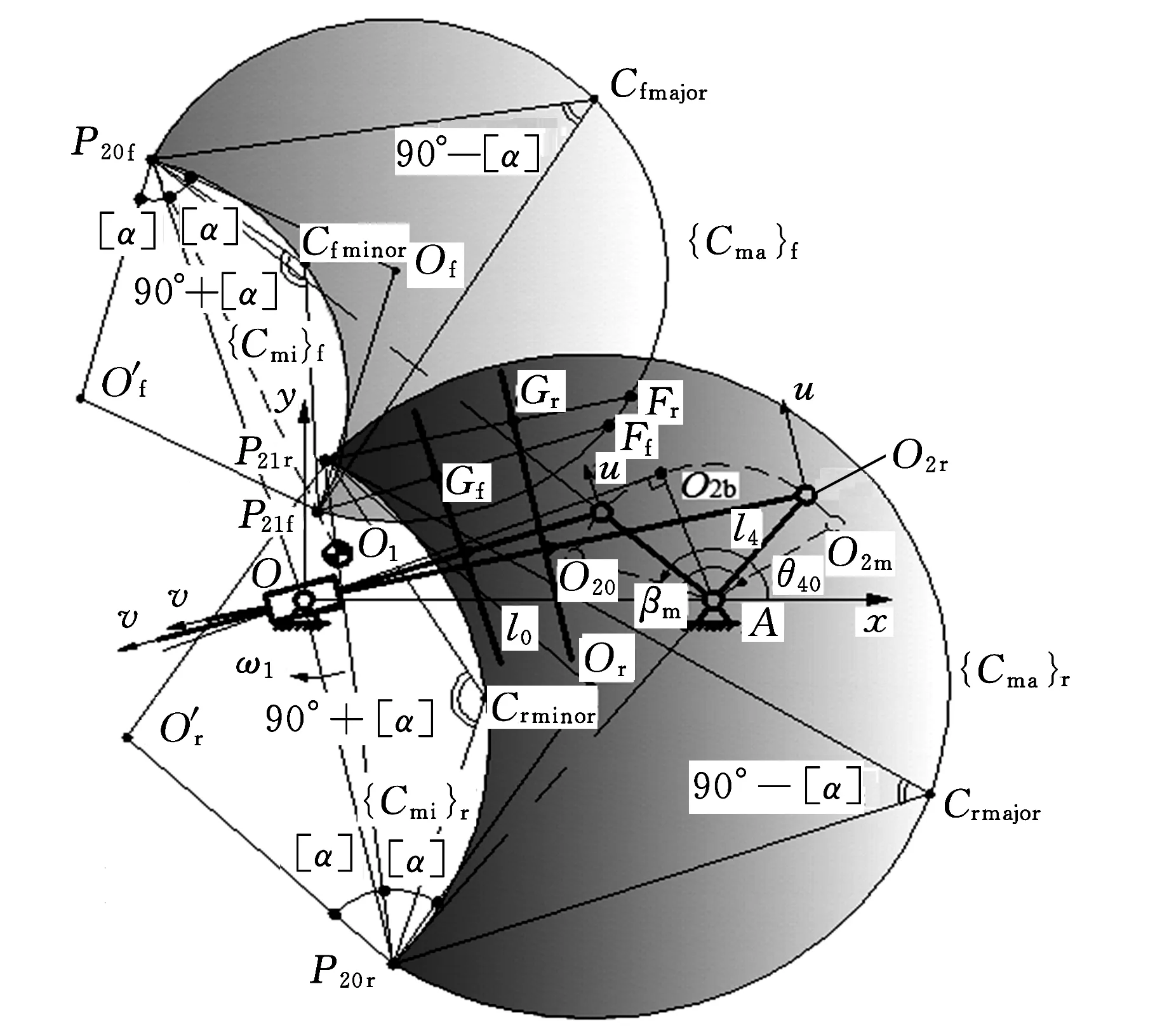
(a)推程
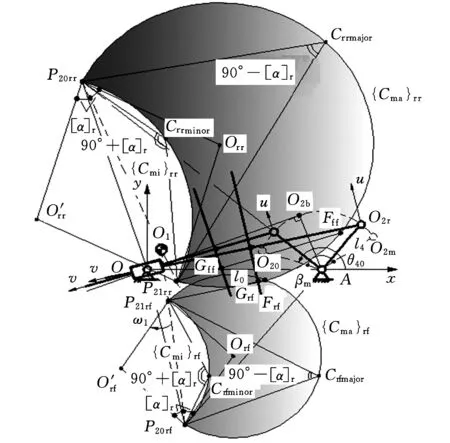
(b)回程圖2 推程和回程前/后半區段劃分和滿足α≤[α]∩α≤[α]r條件的凸輪軸心O1的求解原理(凸輪順時針轉動情形)
2.2浮動坐標系O2u v的建立[2]
浮動坐標系指固連于連桿平面Σ2上,以O2為原點的直角坐標系O2uv。機構運動過程中,O2uv隨連桿平面Σ2做平面運動即“浮動”,如圖1所示。2.3推程前半/后半區段劃分
如圖2所示,P20、P21分別為推程時連桿2的絕對瞬心和相對瞬心,P10為凸輪1的絕對瞬心。
推程前半區段,搖桿4位于O20A、O2bA之間,P20位于OO2上方;推程后半區段,搖桿4位于O2bA、O2mA之間,P20位于OO2下方。分界點O2b滿足O2bA⊥O2bO。此時,P20位于垂直于OO2的無窮遠處。有
cos(180°-θ40+β*)=l4/l0
(15)
β*=arccos(l4/l0)+θ40-180°
(16)
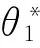
2.4支撐函數法的預備知識[17]
2.4.1凸集的支撐線、支撐函數和方向角
設N為有界閉凸集,邊界?N為閉凸曲線,如圖3所示。任選坐標系O1x′y′,自原點O1引射線O1R,且與x′軸正向夾角為φ(逆時針為正),作垂直于O1R且與N相交的任一直線G1(p1,φ),集合p1的上確界記為p,即
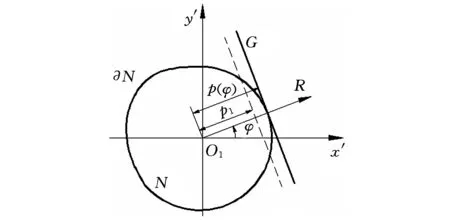
圖3 支撐線、支撐函數與方向角
定義1與p對應的直線G(p,φ)稱作凸集N沿φ方向的支撐線。
定義2與p對應的函數p(φ)稱作凸集N沿φ方向的支撐函數。
定義3與p對應的角度φ稱作支撐線G(p,φ)的方向角。
2.4.2凸集的充要條件
在邊界曲線?N適當定向下,凸集成立的充要條件是曲率半徑ρ恒為正,即
ρ=p(φ)+p″(φ)>00≤φ<2π
(17)
3 滿足ρ>0∩α≤[α]∩α≤[α]r條件的凸輪軸心O1的求解原理和解析表達
探索、建立滿足ρ>0∩α≤[α]∩α≤[α]r條件的凸輪軸心O1的求解原理和解析表達,是本文的一個核心和難點所在。
3.1滿足ρ>0條件的凸輪軸心O1的求解原理和解析表達
本文擬采用支撐函數法[7-8]來解決凸輪輪廓全部外凸即運動保真性問題。
3.1.1凸輪順時針轉動
3.1.1.1推程
如圖4所示,OBO2A、OB0O20A分別為機構任一瞬時位置、推程起始瞬時位置,T、T0為對應的凸輪、平底接觸點。

(a)凸輪順時針轉動
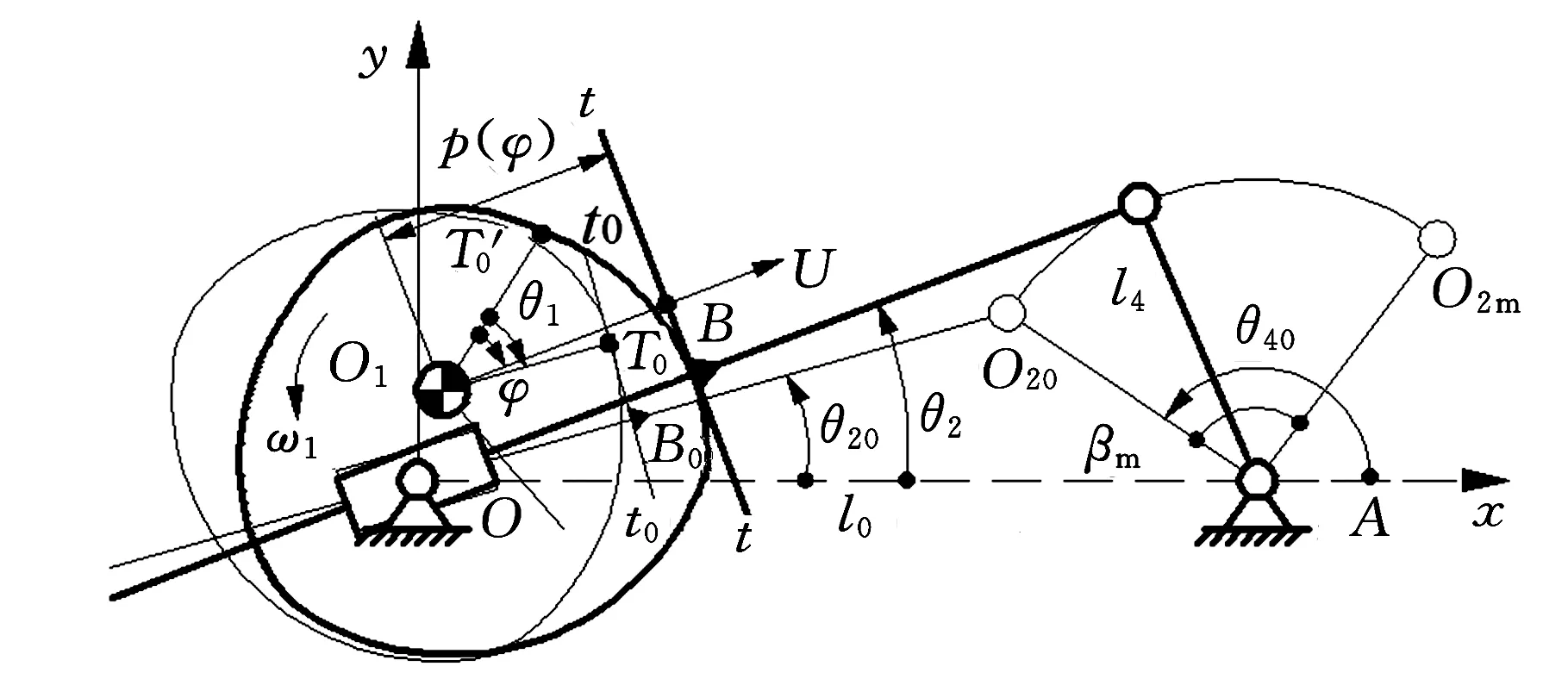
(b)凸輪逆時針轉動圖4 支撐函數、方向角的分析和提取
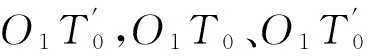
根據解析幾何,點O1到t-t的距離為
O1T′=|cotθ2xO1+yO1-cotθ2xB-yB|sinθ2
(18)
支撐函數為
p(φ)=p(θ1)=O1T′=|cotθ2xO1+
yO1-cotθ2xB-yB|sinθ2
(19)
方向角為
φ=θ1+λ(θ2-θ20)
(20)
式中,λ為轉向系數,凸輪順時針轉動時λ=1,逆時針轉動時λ=-1。
將p(φ)對φ求一階導數:
p′(φ)=dp(φ)/dφ=(dp(φ)/dθ1)/(dφ/dθ1)
(21)
令
D=dp(φ)/dθ1=d(O1T′)/dθ1=
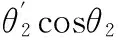
(22)
其中
|A|′=d|A|/dθ1=AA′/|A|
(23)
A=cotθ2xO1+yO1-cotθ2xB-yB
(24)
A′=(xB-xO1)θ2′csc2θ2-yB′-xB′cotθ2
(25)
(26)
(27)
(28)
(29)
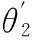
(30)
據式(21)~式(30),有
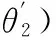
(31)
再將p(φ)對φ求二階導數:
p″(φ)=d2p(φ)/dφ2=dp′(φ)/dφ=
(dp′(φ)/dθ1)/(dφ/dθ1)
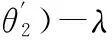
(32)
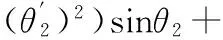
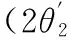
(33)
|A|″=d|A|′/dθ1=AA″/|A|
(34)
csc2θ2-y″B-x″Bcotθ2
(35)
(36)
(37)
(38)
據上,有
p″(φ)=dp′(φ)/dφ=
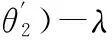
(39)
根據文獻[18],對p(φ)和p″(φ)求和:
ρ=p(φ)+p″(φ)=|cotθ2xO1+yO1-
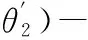
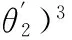
(40)
式(40)為預設凸輪軸心O1(xO1,yO1)時,凸輪輪廓曲率半徑的通用解析計算公式。
據凸輪輪廓全部外凸的條件ρ>0,得
|cotθ2xO1+yO1-cotθ2xB-yB|sinθ2+
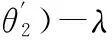
(41)
式(41)為預設凸輪軸心O1(xO1,yO1)時,機構的運動保真條件。
3.1.1.2回程
對于回程,式(18)~式(41)通用,不再贅述。
3.1.2凸輪逆時針轉動
與3.1.1同理,從略。
3.2滿足α≤[α]∩α≤[α]r條件的凸輪軸心O1的求解原理和解析表達
3.2.1凸輪順時針轉動(圖2)
3.2.1.1推程(圖2a)
將整個推程劃分為推程前半區段、后半區段[1-2]進行分析。
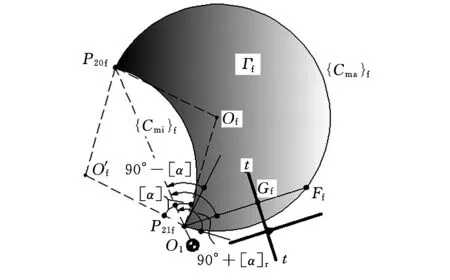
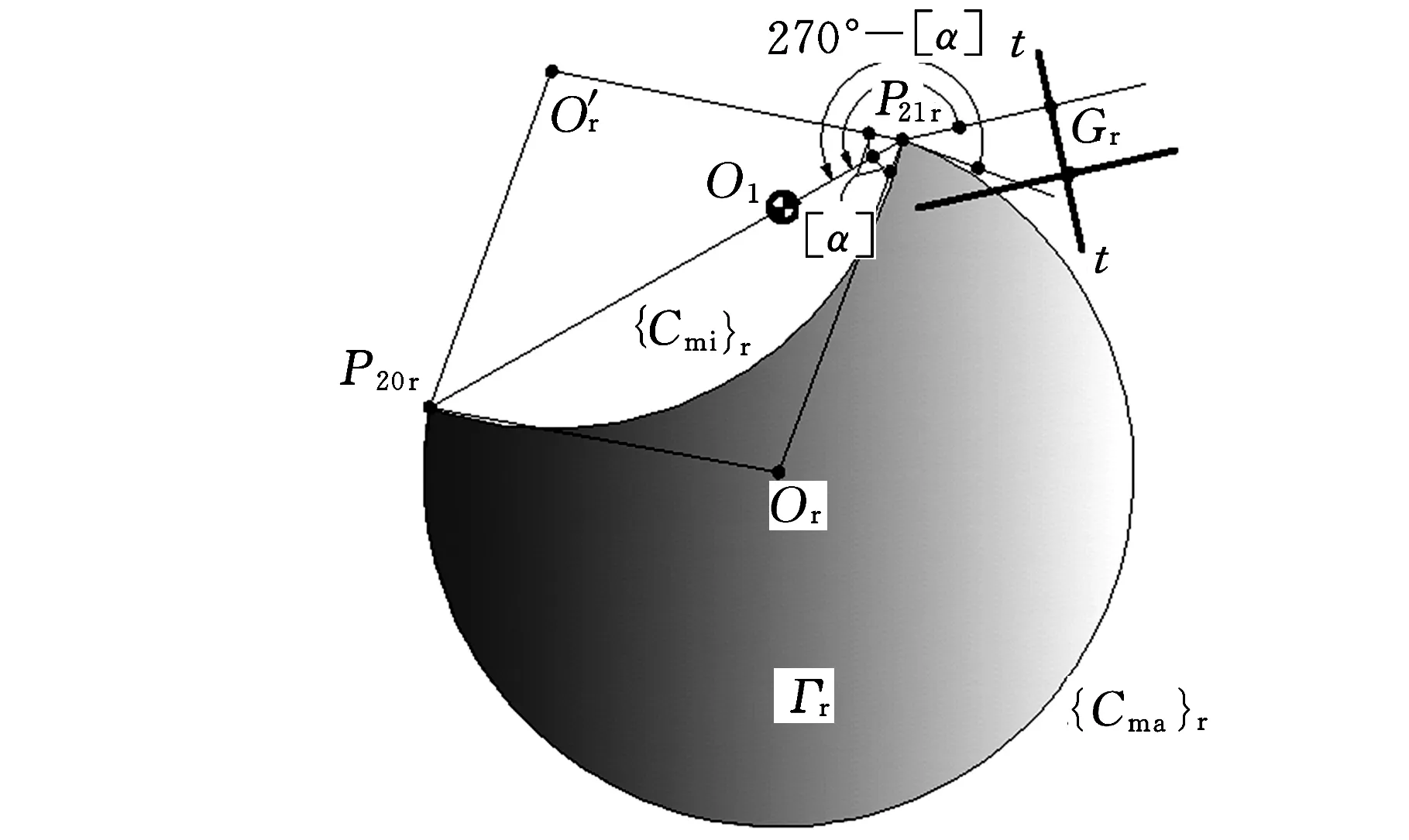
如圖2a所示,任一瞬時位置,在連桿平面Σ2上,以P20P21為弦、朝O2v軸負向作優弧{Cma}、劣弧{Cmi},使其滿足
∠P20CmajorP21=90°-[α]
(42)
∠P20CminorP21=90°+[α]
(43)
根據文獻[2],浮動滾子推桿機構在該瞬時滿足α≤[α]條件的滾子中心點的全集為“瞬時區域套”Γ(u,v),即由{Cma}、{Cmi}合作圍成的“盈月形”二維平面區域(圖2陰影部分)。
過P21引t-t的垂線P21G,得垂足G,G即為該瞬時凸輪、平底接觸點,同時可能得到與{Cmi}、{Cma}的交點E和F。分別選取P21G、P21P20為∠GP21P20的始邊、終邊,則有
∠GP21P20=∠xP21P20-∠xP21G
(44)
式中,∠xP21G和∠xP21P20分別為始邊P21G、終邊P21P20的傾斜角,即有向線段P21G、P21P20沿逆時針與x軸正向的夾角。
特別規定:∠GP21P20沿逆時針方向量取計算,恒為正。理論上,∠GP21P20取值域為
∠GP21P20∈[0,360°)
(45)
根據對象機構的特殊性,恒有
∠xP21G=θ2<90°
(46)
即∠xP21G恒為銳角。
設
ζ=arctan((yP20-yP21)/(xP20-xP21))
(47)
其取值域為ζ∈(-90°,90°)。對應地,∠xP21P20的計算方法有如下3種情況:①xP20-xP21>0、yP20-yP21≥0時,若ζ≥θ2,則∠xP21P20=ζ;若ζ<θ2,則∠xP21P20=360°+ζ;②xP20-xP21<0、yP20-yP21>0時和xP20-xP21<0、yP20-yP21<0時,∠xP21P20=180°+ζ;③xP20-xP21>0、yP20-yP21<0時∠xP21P20=360°+ζ。
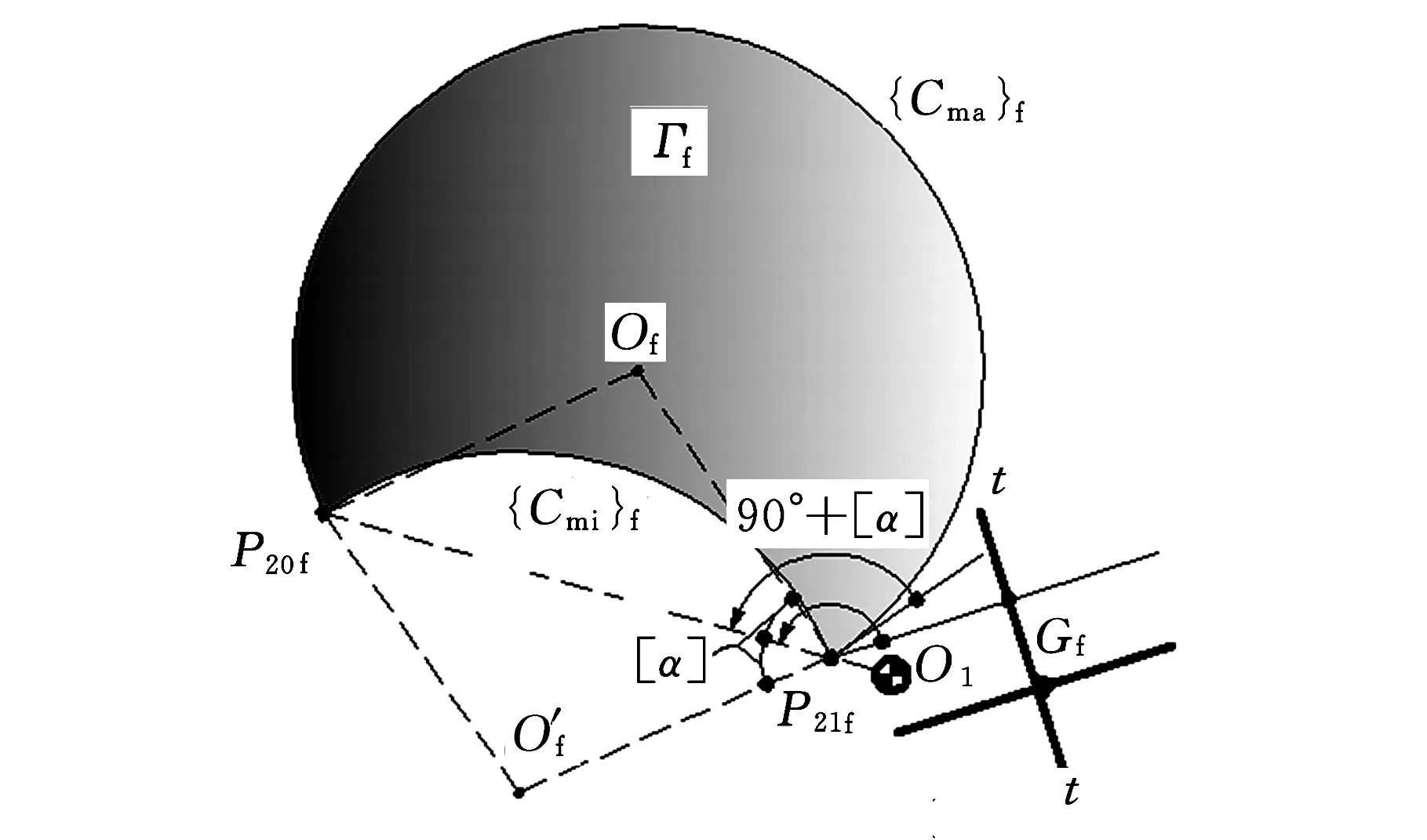
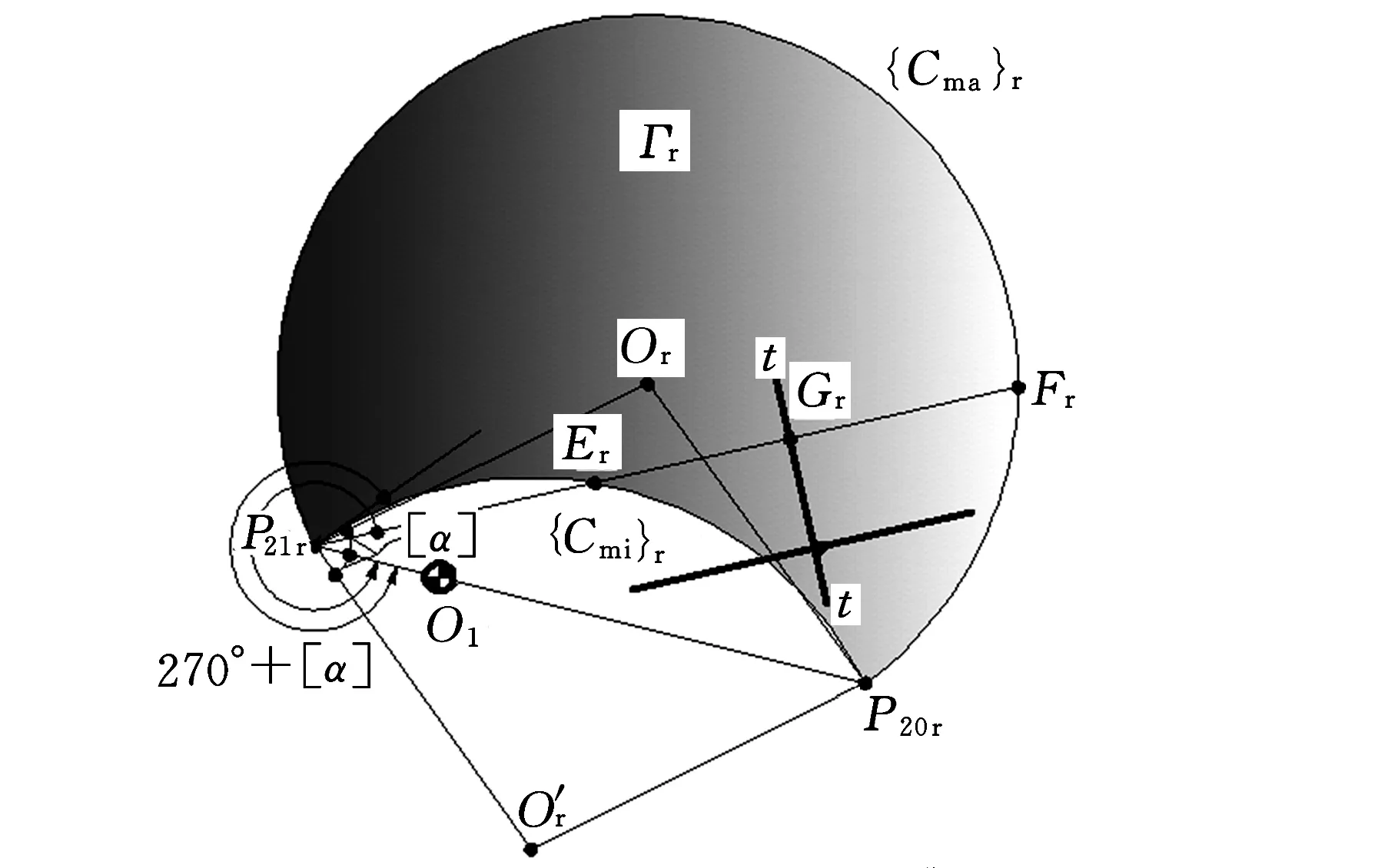
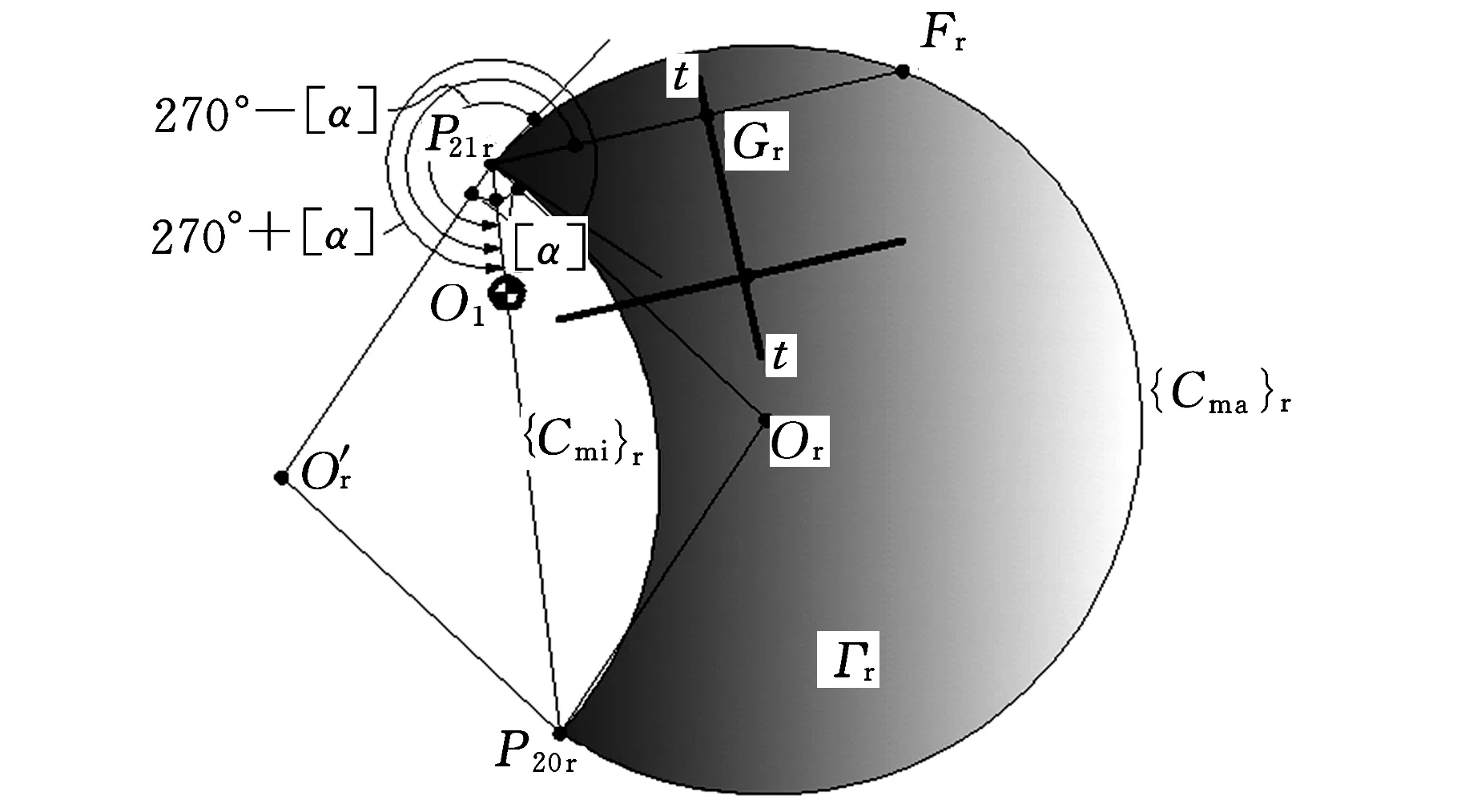
(1)推程前半區段(圖2a)。推程前半區段,P21f位于P20f、O1(P10)之間,如圖2a所示,此時垂足Gf與瞬時區域套Γf(u,v)的相對位置存在下述三種可能情況(圖5):
①0°≤∠GfP21fP20f<90°-[α](圖5a),即Ef、Ff(Ef、Ff為Gf與瞬時區域套Γf(u,v)的兩交點)皆存在。在ΔGfP21fP20f中,據正弦定理,有
P21fEf=f1(θ1)=
l21|cos([α]+η∠GfP21fP20f)|/cos[α]
(48)
P21fFf=f2(θ1)=
l21|cos([α]-η∠GfP21fP20f)|/cos[α]
(49)
式中,η為區段系數,推程前半區段η=1,后半區段η=-1。
根據點到直線距離公式[5],任一瞬時P21f到tf-tf的距離為
P21fGf=f3(θ1)=
|cotθ2xP21+yP21-cotθ2xB-yB|sinθ2
(50)
據式(48)~式(50)知,P21fEf、P21fFf和P21fGf即f1(θ1)、f2(θ1)和f3(θ1)皆為θ1的一元函數。
上述情況又分為兩種情況:
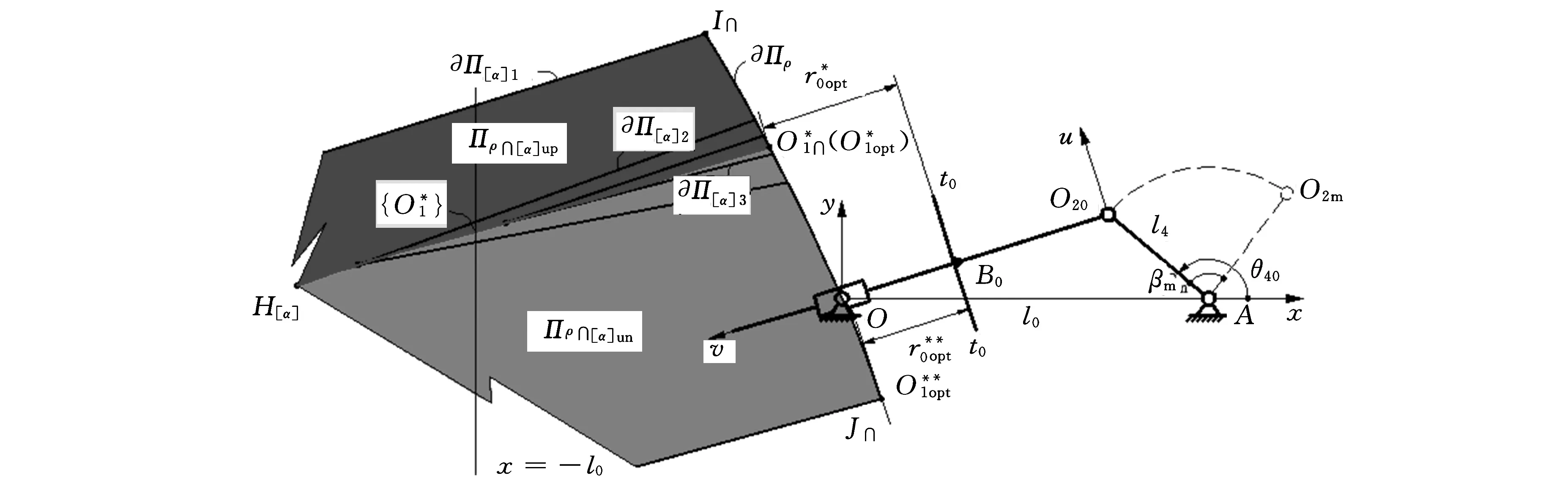
a.P21fEf≤P21fGf≤P21fFf即f1(θ1)≤f3(θ1)≤f2(θ1),此時Gf位于Γf(u,v)內部,滿足α≤[α]條件。該情況下,若P21fEf b.P21fGf ②90°-[α]≤∠GfP21fP20f≤90°+[α](圖5b),即Ff存在、Ef不存在,此時式(50)通用。此情況又分為兩種情況: a.P21fGf≤P21fFf即f3(θ1)≤f2(θ1),此時Gf位于Γf(u,v)內部,滿足α≤[α]條件。該種情況下,若P21fGf b.P21fGf>P21fFf即f3(θ1)>f2(θ1),此時Gf位于Γf(u,v)外部,不滿足α≤[α]條件。 ③90°+[α]<∠GfP21fP20f<360°(圖5c),即Ef、Ff皆不存在,此時G位于Γ(u,v)外部,不滿足 (a)Ff存在,Ef存在 (b)Ff存在,Ef不存在 (c)Ff不存在,Ef不存在圖5 推程前半區段Gf與Γf(u,v)相對位置 α≤[α]條件。 (2)推程后半區段(圖2b)。推程后半區段,P21r位于P20r、O1(P10)延長線上,如圖2b所示。此時Gr與Γr(u,v)的相對位置亦存在三種可能情況(圖6): (a)Fr存在,Er存在 (b)Fr存在,Er不存在 (c)Fr不存在,Er不存在圖6 推程后半區段Gf與Γf(u,v)相對位置 ①270°+[α]<∠GrP21rP20r≤360°(圖6a),此時Er、Fr(Er、Fr為Gr與瞬時區域套Γr(u,v)的兩交點)皆存在,式(48)~式(50)通用,不過,式(48)和式(49)中,η=-1。該情況又分為兩種情況: a.P21rEr≤P21rGr≤P21rFr,此時Gr位于Γr(u,v)內部或{Cmi}r、{Cma}r上,滿足f1(θ1)≤f3(θ1)≤f2(θ1),該瞬時滿足α≤[α]條件。 b.P21rGr ②270°-[α]≤∠GrP21rP20r≤270°+[α](圖6b),即Fr存在、Er不存在,式(50)通用。該情況又分為兩種情況: a.P21rGr≤P21rFr,即Gr位于Γr(u,v)內部或{Cma}r上,滿足f3(θ1)≤f2(θ1),該瞬時滿足α≤[α]條件。 b.P21rGr>P21rFr,即Gr位于Γr(u,v)外部,滿足f3(θ1)>f2(θ1),該瞬時不滿足α≤[α]條件。 ③0°<∠GrP21rP20r<270°-[α](圖6c),即Er、Fr皆不存在,此時Gr位于Γr(u,v)外部,不滿足α≤[α]條件。 綜上所述,得到重要結論:推程任一瞬時,若屬于①a情況或②a情況,則該瞬時滿足α≤[α]條件;反之,該瞬時不滿足α≤[α]條件。 推延、歸納之,得到重要結論:整個推程所有瞬時,無論前半區段還是后半區段,若皆屬①a情況或②a情況,則為滿足α≤[α]條件的凸輪軸心O1;反之,為不滿足α≤[α]條件的凸輪軸心O1。上述“反之”表示“只要某一瞬時不屬于①a情況或②a情況”之意。 3.2.1.2回程 絕大多數情況下,因為[α]r∈(70°,80°),回程時α≤[α]r條件通常可獲得自然滿足,故回程一般可免予考慮。 3.2.2凸輪逆時針轉動(圖4b) 與3.2.1節類似,從略。 如何在“漫無邊界”的機架平面Σ0上挖掘、揭示出滿足ρ>0∩α≤[α]∩α≤[α]r條件的凸輪軸心O1的位置區域,是本文的另外一個關鍵和難點所在。 4.1“經濟搜索區域”的概念及其等距/網格/離散化 顯然,t0-t0將整個機架平面Σ0劃分為左半平面Σ0L和右半平面Σ0R。因凸輪推平底運動,故凸輪軸心O1僅可能位于t0-t0為邊界的平面Σ0L上,不可能位于t0-t0為邊界的平面Σ0R上。 如圖7所示,絕對瞬心線{P20}由{P20}up和{P20}un上下兩分支構成,分別對應推程前半區段和后半區段。 圖7 滿足ρ>0條件的凸輪軸心O1的位置區域 研究發現,與推程始點、終點瞬時對應的絕對瞬心P20S、P20E分別位于{P20}up、{P20}un的最低點、最高點,即 (51) 根據上述分析,提出并認定凸輪軸心O1必位于如下“經濟搜索區域Ω”內: (52) 式中,xt0為t0-t0上點的x坐標;yP20S、yP20E分別為P20S和P20E的y坐標。 式(52)的隱性涵義是:t0-t0為邊界的左半平面Σ0L的y=yP20S以下、y=yP20E以上兩子區域的所有點,皆屬3.2節的情況①b、②b或情況③。證明從略。 不言而喻,經濟搜索區域Ω是有限區域,左半平面是無限區域,前者是后者的子區域。顯而易見,經濟搜索區域Ω呈現梯形的形態特征。 經濟搜索區域Ω的提出,在確保O1位置區域完整、無缺失前提下,大大縮小了搜索范圍,顯著提高了求解效率。 現在,對經濟搜索區域Ω進行等距、網格、離散化處理,具體步驟如下: (1)以y=0(橫軸)為基準,分別朝上、朝下作等距、離散平行的直線族{yj},其方程為 y=yj=jΔyj=jmin,…,-1,0,1,…,jmax (53) 且有 jmax=ent(yP20S/Δy) (54) jmin=ent(yP20S/Δy) (55) 式中,Δy為相鄰兩直線y=yj、y=yj+1間的距離。 (2)以x=0(縱軸)為基準,分別朝左、朝右作等距、離散平行直線族{xi},其方程為 x=xi=iΔxi=imin,…,-1,0,1,…,imax (56) 且有 imax=ent(xt0/Δx) (57) imin=ent(-l0/Δx) (58) 式中,Δx為相鄰兩直線x=xi、x=xi+1間距離。 (3)正交單元網格的邊長為 Δx=Δy=10-p(mm) (59) 式中,p=1,2,…,根據精度要求確定。 通過等距、網格、離散化處理后,Ω由連續、無數點轉化為離散、有限點的網格節點族{(xi,yj)},如圖7所示。(xi,yj)即表示兩直線x=xi、y=yj相交得到的任一網格節點。 4.2滿足ρ>0條件的凸輪軸心O1的位置區域及其形態特征 4.2.1凸輪順時針轉動 對于網格節點族{(xi,yj)},自y=yjmin到y=yjmax逐層、各層自x=ximax到x=ximin逐節點作遍歷性計算,校核推程、回程是否皆滿足運動保真條件,若滿足,則將點{(xi,yj)}保存,否則舍棄。于是,可得到滿足ρ>0條件的凸輪軸心O1的位置區域Πρ即網格節點集合{(xi,yj)}ρ>0。 大量案例計算表明:位置區域Πρ為有一條朝 左開放邊界?Πρ的解區域,如圖7所示。 4.2.2凸輪逆時針轉動 同理,從略。 4.3滿足α≤[α]∩α≤[α]r條件的凸輪軸心O1的位置區域及其形態特征 4.3.1凸輪順時針轉動 同4.2.1節,自y=yjmin到y=yjmax逐層、各層自x=ximax到x=ximin逐節點作遍歷性計算,校核整個推程是否皆滿足運動保真條件,若皆滿足運動保真條件則保存{(xi,yj)};否則舍棄之。于是,得到滿足α≤[α]∩α≤[α]r條件的凸輪軸心O1的位置區域Π[α]即網格節點集合{(xi,yj)}α≤[α]。 根據大量案例的求解計算,得到如下重要結論: (1)位置區域Π[α]的形態特性。Π[α]具有類似等腰三角形的形態特征。上下兩腰HI、HJ和底邊IJ(在t0-t0上)構成邊界?Π[α],如圖8所示。 圖8 滿足α≤[α]∩α≤[α]r條件的凸輪軸心O1的位置區域 若記頂點為H[α](x[α]a,y[α]a),則有x[α]a=min{xi}Π[α],min{xi}Π[α]為Π[α]中所有網格節點x坐標的最小者。 對于兩腰HI、HJ上的點,有α=[α];而對于底邊IJ上的點,有α≠[α]。對于上腰HI,從H到I諸點,基圓半徑r0呈單調遞減變化,在I處取得最小值。對于下腰HJ,從H到J諸點,基圓半徑r0亦呈單調遞減變化,在J處取得最小值。 根據圖8,有r0I>r0J,故滿足α=[α]條件時有r0J=min{r0[α]},min{r0[α]}為滿足α=[α]條件的所有凸輪軸心O1的凸輪基圓半徑。 (2)Π[α]、?Π[α]的收縮聚斂特性。取不同[α]值,對應得到Π[α]1、Π[α]2和Π[α]3,若[α]3≤[α]2≤[α]1,則Π[α]1?Π[α]2?Π[α]3,?Π[α]1??Π[α]2??Π[α]3,表明:隨[α]值減小,Π[α]、?Π[α]不斷收縮,[α]小者恒嵌套于大者內部。 cotθ20x+y-cotθ20xB0-yB0+cscθ20kΔt=0 (60) k=1,2,…,kmax 其中,Δt為相鄰兩直線tk-tk、tk+1-tk+1間距離,考慮到與前面Δx、Δy匹配,亦取Δt=10-p(mm)且有kmax=ent(yP20S/Δt)。 取直線tk-tk上任一點為凸輪軸心O1,則其具有相同的基圓半徑r0k,且有 r0k=lk=kΔtk=1,2,…,kmax (61) 在直線族{tk-tk}(k=1,2,…,kmax)中任取一條直線tk-tk,分別與?Π[α]1、?Π[α]2截交各得兩個交點D[α]1up、D[α]1un和D[α]2up、D[α]2un,顯然[D[α]2un,D[α]2up]?[D[α]1un,D[α]1up]。 (62) 以[α]為變量進行一維搜索,直至得到[α]k,若記與之對應的Π[α]k的頂點為H[α]k(x[α]ka,y[α]ka),則據式(14),滿足 |cotθ20x[α]ka+y[α]ka-cotθ20xB0-yB0|sinθ20-kΔt=0 (63) 4.3.2凸輪逆時針轉動 同理,從略。 4.4滿足ρ>0∩α≤[α]∩α≤[α]r條件的凸輪軸心O1的位置區域及其形態特征 4.4.1凸輪順時針轉動 4.4.1.1位置區域Πρ∩[α]的形態特征 基于4.2節和4.3節,得到交集 {(xi,yj)}ρ>0∩α≤[α]= {(xi,yj)}ρ>0∩{(xi,yj)}α≤[α] (64) 該交集即是滿足ρ>0∩α≤[α]∩α≤[α]r條件的位置區域Πρ∩[α]。 如圖9所示,位置區域Πρ∩[α]呈現組合、封閉的形態特征。 圖9 滿足ρ>0∩α≤[α]∩α≤[α]r條件的凸輪軸心O1的位置區域 具體說來,凸輪軸心O1的位置區域仍具有類三角形的區域形態特征。三個頂點分別是H[α]、I∩和J∩。I∩和J∩就是?Πρ與?Π[α]截交得到的兩個交點。 4.4.1.2凸輪軸心O1的優選(非劣)解集 證明從略。 值得指出的是,4.4.1.2~4.4.1.4節選擇凸輪軸心O1僅考慮了r0和α兩個性能參數,存在片面、偏頗之處。工程實際中,除考慮r0和α外,還須兼顧考慮平底工作段分布,以及機構橫向、縱向尺寸的合理分配等。不難想象,后兩者對機構的運動平穩性、動力學特性以及運動空間等皆會產生重要影響。 4.4.2凸輪逆時針轉動 求解方法與凸輪順時針轉動情形類似,不再贅述。 5.1浮動平底工作段的求解確定 平底工作段指機構整程中浮動平底與凸輪輪廓實際接觸的區段。 5.1.1凸輪順時針轉動 如圖2a所示,OBO2A為機構處于任一瞬時的位置。P21G的方程為y-yP21=tanθ2(x-xP21),xP21、yP21可據式(7)、式(8)算得。 將P21G的方程y-yP21=tanθ2(x-xP21)與式(18)聯立,解得凸輪、平底接觸點G在固定系Oxy中的坐標為 (65) xB、yB可據式(11)算得。 根據坐標變換原理,得G在浮動系O2uv中的坐標: (66) xO2、yO2可據式(6)算得。 由式(66)可知,uG是θ1的一元函數,vG是常值。 綜合考慮推程、回程,一維搜索解得uG的最大和最小值分別為uGmax和uGmin,從而解得平底工作段uG∈[uGmin,uGmax]。 5.1.2凸輪逆時針轉動 同理,從略。 5.2浮動平底工作段長度、總長度的求解確定 5.2.1凸輪順時針轉動 平底工作段長度為l=uGmax-uGmin,平底總長度為L=l+(5~7)mm。 5.2.2凸輪逆時針轉動 同理,從略。 解: (1)據已知條件特別是第3、第4章求解理論方法,取p=2,通過編程搜索求解,解得凸輪軸心位置區域Πρ∩[α],如圖9所示。也就是說,圖9是據例題已知條件數據,通過計算機搜索求解自動生成的。 [1]常勇,楊富富.作平面運動滾子從動件盤形凸輪機構的第Ⅱ類機構綜合問題[J].機械工程學報,2010,46(21):37-41. ChangYong,YangFufu.SecondMechanismSynthesisTaskofDiscCamMechanismswithRollerFollowerMovinginPlanarGeneralMotion[J].JournalofMechanicalEngineering,2010,46(21):37-41. [2]常勇,楊富富,李延平,等.作平面運動滾子從動件盤形凸輪機構的廣義第Ⅱ類機構綜合問題[J].機械工程學報,2012,48(15):47-57. ChangYong,YangFufu,LiYanping.ResearchonSecondMechanismsSynthesisTaskofPositive-driveDiscCamMechanismswithRollerFollowerMovinginGeneralPlanarMotion[J].ChineseJournalofMechanicalEngineering,2012,48(15):47-57. [3]常勇,楊富富.作平面運動滾子從動件形鎖合凸輪機構的第Ⅱ類機構綜合問題[J].機械工程學報,2012,48(1):39-46. ChangYong,YangFufu.SecondMechanismsSynthesisTaskofPositive-driveDiscCamMechanismswithRollerFollowerMovinginGeneralPlanarMotion[J].ChineseJournalofMechanicalEngineering,2012,48(1):39-46. [4]常勇,李延平,劉國祥.按許用壓力角設計最小尺寸作平面復雜運動滾子從動件平面凸輪機構的解析法[J].機械工程學報,1991,27(4):37-41. ChangYong,LiYanping,LiuGuoxiang.TheAnalyticsforDesigningMinimumSizeDiscCamMechanismsWhoseRollerFollowerMovinginGeneralPlanarMotionaccordingtoAllowablePressureAngle[J].ChineseJournalofMechanicalEngineering,1991,27(4):37-41. [5]常勇,林榮富,李延平.作平面運動平底從動件盤形凸輪機構第Ⅱ類機構綜合[J].農業機械學報,2013,44(7):286-292. ChangYong,LinRongfu,LiYanping.ClassⅡSynthesisofDiscCamMechanismwithFlat-facedFollowerinPlanarMotion[J].TransactionsoftheChineseSocietyforAgriculturalMachinery,2013,44(7):286-292. [6]常勇,林榮富,李延平.做平面運動滾子從動件盤形凸輪機構的深度廣義第Ⅱ類綜合問題[J].中國機械工程,2014,25(16):2149-2158. ChangYong,LinRongfu,LiYanping.GeneralClassⅡSynthesisofDiscCamMechanismwithRollerFollowerMovinginPalnarGeneralMotion[J].ChinaMechanicalEngineering,2014,25(16):2149-2158. [7]馬喜川, 常勇, 李延平. 支撐函數在機構學中的若干重要應用[J].機械設計, 1996, 13(10): 24-26. MaXichuan,ChangYong,LiYanping.TheSeveralImportantApplicationsofSupportFunctioninMechanisms[J].JournalofMachineDesign,1996,13(10):24-26. [8]SchoenherrJ.SynthesisofPlanarCamMechanicswithLowestDimensions[J].MechanismandMachineTheory,1993,28(3):317-325. [9]NavarroO,WuCJ,AngelesJ.Size-minimizationofPlanarCamMechanisms[J].MechanismandMachineTheory,2001,36(3):371-386. [10]DasguptaA,GhostA.OntheDeterminationofBasicDimensionsofaCamwithaTranslatingRoller-Follower[J].JournalofMechanicalDesign,Trans.ASME,2004,126(1):143-147. [11]CarraS,GarzieraR,PellegriniM.SynthesisofCamswithNegativeRadiusFollowerandEvaluationofthePressureAngle[J],MechanismandMachineTheory,2004,39:1017-1032. [12]JiZ,MannaYA.SizeMinimizationofDiscCamswithRoller-followersunderPressureAngleConstraint[J].MechanicalEngineeringScience,Imeche,2008,222(12):2475-2484. [13]華大年.按許用壓力角設計最小尺寸的擺動從動桿平面凸輪機構的解析法[J].機械工程學報,1982,18(4):74-79.HuaDanian.TheAnalyticsforDesigningMinimumSizeDiscCamMechanismswithOscillatingFolloweraccordingtoAllowablePressureAngle[J].ChineseJournalofMechanicalEngineering,1982,18(4):74-79. [14]常勇,吳從炘,李延平.關于《按許用壓力角設計最小尺寸的擺動從動桿平面凸輪機構的解析法》一文的兩點注記[J].黑龍江商學院學報(自然科學版),1989,5(2):49-54. ChangYong,WuCongxin,LiYanping.TheFurtherNoteson“theAnalyticsforDesigningMinimumSizeDiscCamMechanismswithOscillatingFolloweraccordingtoAllowablePressureAngle”[J].JournalofHeilongjiangCommercialCollege,1989,5(2):49-54. [15]王知行,李瑰賢.關于直動滾子從動件盤形凸輪基本尺寸的討論[J].機械工程學報,1986,22(4):88-93. WangZhixing,LiGuixian.DiscussiononFundamentalSizeofTranslatingFollowerDiscCamMechanisms[J].ChineseJournalofMechanicalEngineering,1986,22(4):88-93. [16]呂庸厚,沈愛紅.組合機構設計與應用[M].北京:機械工業出版社,2008. [17]吳家欽,奚定華.平面解析幾何[M].上海:上海科學技術出版社,1982. [18]任德麟.積分幾何學引論[M].上海:上海科學技術出版社,1988. (編輯蘇衛國) Class Ⅰ Synthesis of Cam Mechanism with Floating Flat Faced Pushrod Chang YongLin RongfuLi Yanping Jimei University,Xiamen,Fujian,361021 equidistant/grid/discretization;floating coordinate system;support function;instantaneous area set;economic searching area;ridge point/ridge line 2013-11-14 2015-04-15 國家自然科學基金資助項目(51175224);福建省自然科學基金資助項目(2010J01302,2006J0169) TH112.2DOI:10.3969/j.issn.1004-132X.2015.12.004 常勇,男,1964年生。集美大學機械工程學院教授。研究方向為凸輪與連桿機構學、機構的起源與進化理論等。發表論文160篇。林榮富,男,1987年生。集美大學機械工程學院助教。李延平(通信作者),女,1963年生。集美大學機械工程學院教授。
4 凸輪軸心O1的位置區域及其形態特征
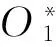
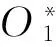
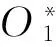
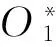
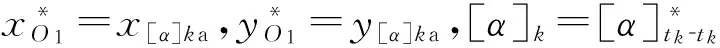
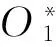

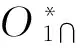
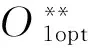
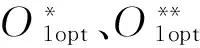
5 浮動平底工作段及其長度、總長度的求解確定
6 機構綜合示例