高速數控加工中NURBS曲線擬合及插補技術的研究

楊　萍　楊明泰　張陽陽

蘭州理工大學,蘭州,730050

高速數控加工中NURBS曲線擬合及插補技術的研究

楊萍楊明泰張陽陽

蘭州理工大學,蘭州,730050

通過分析現代數控系統中自由曲面插補算法的特點，提出了基于最小二乘法的NURBS曲線擬合算法和基于弧長參數補償的NURBS插補技術。采用最小二乘法擬合NURBS曲線，能獲得光滑的刀具加工路徑,并且在一定范圍內能復原曲線的設計輪廓。參數補償的NURBS插補方法，以泰勒展開法得到的插補參數作為臨時插補點,利用該插補法能顯著減小速度波動，可將速度控制在理想的范圍內,可進一步提高加工精度并減小數控機床的振動。仿真實驗表明：該算法簡明高效、易于實現，能夠滿足現代數控系統的要求。

CNC;NURBS曲線;最小二乘法;參數補償

0　引言

隨著制造業的快速發展，超高速、高精度、高柔性的加工技術已成為現代數控加工領域新的研究方向。傳統的計算機數控(computer numerical control,CNC)系統在加工自由曲面時,主要采用直線或圓弧插補方式,由CAM系統進行離線編程，再將參數曲線離散成許多直線段或圓弧段構成的程序傳輸到CNC系統完成插補，采用這種插補方式勢必會降低零件的加工精度和表面質量,也限制了數控系統的加工效率[1-2]。另外，用小線段擬合刀具的軌跡本身就會導致加工表面不光滑且插補誤差難以控制，在加工過程中刀具頻繁的加減速使得機床的穩定性大大降低，進而加劇了刀具的磨損。現代數控加工中可以將自由曲面的參數直接傳輸到CNC系統中，不再分割成若干小線段或圓弧段，從而使CAD/CAM/CNC之間保持完整的參數信息流。當前NURBS直接插補算法已成為高速、高精度加工的研究熱點[3]。

國內外學者對NURBS曲面插補技術作了許多研究,例如:Nam等[4]提出了實時控制加加速度,使加速度控制在約束范圍內的插補算法。Shiuh等[5]提出了自動調節進給速度的限定弓高誤差的NURBS插補算法。Shpitalni等[6]和Yang等[7]提出用泰勒展開式一階與二階近似的方式獲取NURBS插補數據,從而進一步減小速度的波動。Park等[8]提出了一種分階段的方式來處理NURBS插補算法。周紅梅等[9]提出了自適應選擇節點數量的NURBS擬合算法，該算法是通過曲率的信息來確定節點數的，最后通過de Boor迭代法來獲取控制點。本文在前人的研究基礎之上提出了基于最小二乘的NURBS樣條擬合算法，使得擬合后的曲線具有較高的精度指標,進而,針對更高精度的需求,提出了基于弧長參數補償的NURBS插補技術。

1　NURBS曲面上曲線的數學表達式

一條k次NURBS曲線可以表示為一分段有理多項式矢函數:

(1)

式中,u為NURBS曲線的自變量;Di為控制頂點(i=0,1,2,…,n)，Di順序連接成控制多邊形;ωi為權因子,分別與控制頂點相對應,ωn>0,其余ωi≥0,且權因子不同時為零(由此可保留凸包性質和防止分母為零);Ni,k(u)是定義在非周期節點矢量U上的k次B樣條基函數,U=(u0,u1,…,un+k+1)。

一條NURBS曲線由控制點、節點矢量、權因子和基函數的次數4個參數來決定。

2　最小二乘法的NURBS曲線擬合算法

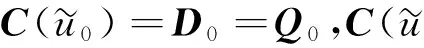
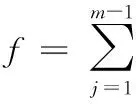
(2)

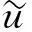
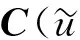
(3)

(4)

應用標準的線性最小二乘擬合技術,欲使目標函數f最小,應令f關于n-1個未知控制點Dl(l=1,2,…,n-1)的偏導數都等于零。它的第l個偏導為

(5)

即

(6)

于是

(7)

式(7)是一個控制點D1,D2,…,Dn-1為未知量的線性方程。讓l=1,2,…,n-1,則得到含n-1個該未知量的n-1個方程的方程組,寫成矩陣形式為

(NTN)D=R

(8)

其中,N是(m-1)×(n-1)矩陣:

(9)

R和D分別為

R=

D=[D1D2…Dn-1]T

(10)

式(8)中的矩陣(NTN)是正定的,可以用高斯消元法來求解控制點。在規定精度范圍內的曲線逼近，控制點的個數選取決定著曲線的最優程度,一般用k+1個控制點(這里是最少的)作為迭代的開始，用式(3)、式(8)和式(10)對數據點進行擬合得到一條逼近曲線，每次擬合之后可以根據最大模偏差公式檢查曲線偏差是否小于逼近誤差E，直至滿足設定的逼近誤差E。當刀位點數與控制點數相等時,逼近誤差E=0。最大模偏差公式為

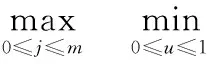
(11)

本文對離散刀位點進行最小二乘擬合,對數據點進行了仿真實驗。圖1結果表明，使用最小二乘法的NURBS曲線擬合方法原理簡明,易于實現,并且具有很高的擬合精度，與其他擬合方法相較有明顯的優勢。

圖1　NURBS曲線的最小二乘擬合

3　基于弧長參數補償的NURBS插補技術

3.1預處理及誤差分析

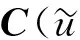
(12)

i=0,1,2,…,n-3

u∈[ui,ui+1]

令

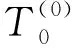
(13)

在插補過程中,要想得到較高插補精度,必須滿足插補速度平穩、速度波動小的要求,即插補時的合成實際速度要與給定的進給速度相一致,本文將進給速度與輪廓誤差作為插補好壞的評價標準。在NURBS曲線插補過程中,通常利用插補點的曲率來計算參數ui處的輪廓誤差Ei。

圖2是用一段圓弧近似地表示在區間u∈[ui,ui+1]內的NURBS曲線,ρi為曲率半徑,且ρi=1/Ki,插補周期為T,并令Li=‖C(ui+1)-C(ui)‖,進給速度為v(ui),通過幾何關系可以求出輪廓誤差:

(14)

其中該點的曲率半徑計算如下:

(15)

圖2　誤差求解幾何關系

假設加工過程中要求最高輪廓誤差為δ,則在要求誤差下的進給速度為

(16)

如果Ei滿足Ei≤δ,插補計算過程將繼續進行下一個點的插補計算;如果Ei滿足Ei>δ,插補過程將會調整插補進給速度v(ui),返回當前插補點,按調整后的進給速度重新進行下一個點的插補計算。在NURBS曲線插補過程中,可以通過調整進給速度來調節規定范圍內的加工精度。

3.2實時插補算法

傳統的NURBS插補技術常用的是泰勒展開法,這種方法難以滿足以弧長為參數的插補,并且NURBS插補過程中計算復雜,速度不能平滑過渡,為了能夠滿足插補過程中計算量小的要求,并實現高精度的快速實時插補,筆者提出了基于弧長參數補償的NURBS插補技術。其方法是以泰勒展開法得到的插補參數作為臨時插補點,對臨時插補點進行參數補償，以確保原曲線弧長為插補參數。假設空間參數曲線為C(u)=x(u)i+y(u)j+z(u)k,u是曲線參數。則插補進給速度v(ui),可以表達為

(17)

可以進一步推導求得:

(18)

變量u在u=ui處的一階泰勒展開式為

(19)

式中,Ts為插補周期;R(u)為誤差余量。

則有

(20)

式(20)是通過一階泰勒展開方法得到的下一個插補點的求解式。若ti在所在領域內二階導數是連續的,此時可以求其二階導數:

(21)

變量u在u=ui處的二階泰勒展開式為

(22)

則有

(23)

式(21)是通過二階泰勒展開方法得到的下一個插補點的求解式。

從得到的一階、二階泰勒展開式可以看出泰勒展開法的本質也是弧長與參數的關系，但是泰勒展開式中省略了誤差余量，導致了弧長與參數的關系式表達不完全精確。可以用基于弧長參數補償的NURBS插補技術來完善這個問題，具體操作步驟是根據插補點的位置坐標、一階導數、二階導數三者之間的關系，在插補的前一個點和臨時插補點之間建立弧長與參數的三次多項式或更高次多項式，使得插補以弧長為基準。

NURBS曲線參數u與弧長S的三次多項式可表達為:u=a+bS+cS2+dS3,進行參數插補的前提是計算臨時參數值,以一階泰勒插補為起點:

(24)

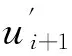
(25)

式(25)可簡寫為

δ=φ·φ

由此可得系數矩陣φ有唯一解φ=φ-1·δ。

假設插補進給速度為v(ui),插補周期內的位移Si=v(ui)Ts,則參數ui+1計算式為

(26)

結合式(25)就可求解出a、b、c、d4個系數。弧長與參數的五次多項式也可以用同樣的方法求解。

4　仿真結果與性能分析

為了驗證本文所提出算法的有效性和正確性，采用MATLAB對空間NURBS曲線進行仿真計算。由于進給速度波動率是評價插補性能的關鍵因素之一，因此主要對插補過程中的進給速度波動進行仿真計算。空間NURBS曲線的參數如下：空間曲線的次數為3,控制點為(0,0,0)、(3.5,12,2)、(12,22.5,6)、(17,18.5,8)、(19,9.75,9)、(25,12,10.25)、(30,21,12)、(38,11.75,14)、(45,0,11)(單位為mm),節點矢量(0,0,0,0,1/7,2/7,3/7,4.1/7,5/7,5/7,1,1,1,1)(mm),權重(1,1,1,1,1,1,1,1)，進給速度vs=63 mm/s,不考慮加減速,插補周期Ts=1.8 ms,空間NURBS曲線如圖3所示。

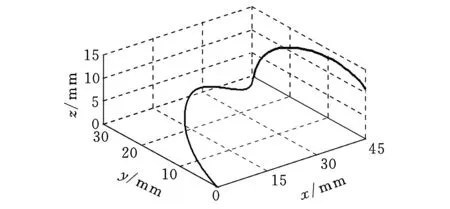
圖3　空間NURBS曲線

插補方法采用一階、二階泰勒展開法,以及三次、五次多項式的參數補償插補法。速度波動計算公式為

圖4　一階泰勒方法速度波動圖

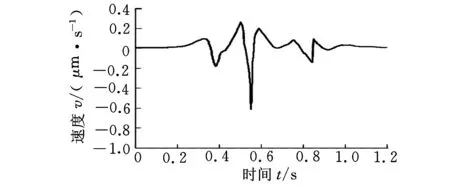
圖5　二階泰勒方法速度波動圖

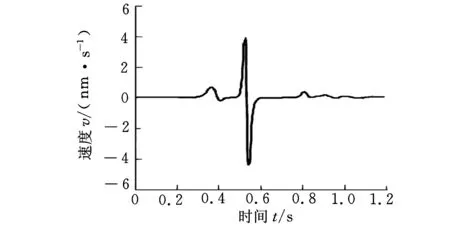
圖6　三次多項式補償速度波動曲線

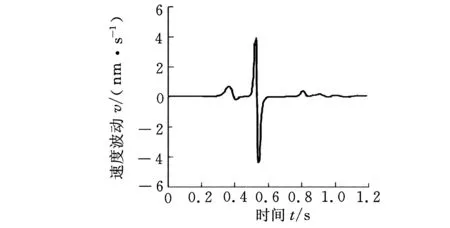
圖7　五次多項式補償速度波動曲線

(27)

通過分析對比仿真結果(圖4～圖7)可以得出以下結論:①參數補償插補方法與泰勒插補方法相比較,參數補償插補方法能顯著減小速度波動，能使速度控制在理想的范圍內,可進一步提高加工精度和減小數控機床的振動。②根據仿真數據可以分析得出參數的補償有可能是負值或者是正值，在曲率比較大的地方為了減小速度的波動可以提高速度。

[1]梁宏濱,王永章,李霞.自動調節進給速度的NURBS插補算法的研究與實現[J].計算機集成制造系統,2006,12(3):428-433.

Liang Hongbing,Wang Yongzhang,Li Xia.Research and Implementation of NURBS Interpolation Algorithm for Adaptive Feed Speed[J].Computer Integrated Manufacturing Systems,2006,12(3):428-433.

[2]Cheng M Y,Tsai M C,Kuo J C.Real-time NURBS Command Generators for CNC Servo Controllers[J].Machine Tools & Manufacture,2002,42(7):801-813.

[3]劉宇,趙波,戴麗,等.基于傳動系統動力學的NURBS曲線插補算法[J].機械工程學報,2009,45(12):187-191.

Liu Yu,Zhao Bo, Dai Li.Feedrate System Dynamics Based Interpolator for NURBS Curve[J].Journal of Mechanical Engineering,2009,45(12):187-197.

[4]Nam S H,Yang M Y.A Study on a Generalized Parametric Interpolator with Real-time Jerk-limited Acceleration[J].Computer-Aided Design,2004,36(1):27-36．

[5]Shiuh S,Hsu P L.Adaptive-feedrate Interpolation for Parametric Curves with a Confined Chord Error[J].Computer-aided Design,2002,34(3):229-237．

[6]Shpitalni M,Koren Y,Lo C C.Real-time Curve Interpolators[J].Computer-Aided Design,1994,26(11):832-838.

[7]Yang D C H,Kong T.Parametric Interpolator Versus Linear Interpolator for Precision CNC Machining[J].Computer-Aided Design,1994,26(3):225-234.

[8]Park J,Nam S,Yang M.Development of a Real-time Traj-ectory Generator for NURBS Interpolation Based on the Two-stage Interpolation Method[J].The International Journal of Advanced Manufacturing Technology,2005,26(4):359-365.

[9]周紅梅,王燕銘,劉志剛,等.基于最少控制點的非均勻有理B樣條曲線擬合[J].西安交通大學學報,2008,42(1):73-77.

Zhou Hongmei,Wang Yanming,Liu Zhigang,et al.Non-Uniform Rational B-splines Curve Fitting Based on the Least Control Points[J].Journal of Xian Jiaotong University,2008,42(1):73-77.

[10]游有鵬,王珉,朱劍英.NURBS曲線高速高精度加工的插補控制[J].計算機輔助設計與圖形學學報,2001,13(10):943-947.

You Youpeng,Wang Min,Zhu Jianying.An Interpolator for NURBS Curve Machining with High-speed and Accuracy[J].Journal of Computer-aided Design & Computer Graphics，2001，13(10):943-947.

(編輯盧湘帆)

Research on Technologies of NURBS Curve Fitting and Interpolation in High Speed NC Machining

Yang PingYang MingtaiZhang Yangyang

Lanzhou University of Technology,Lanzhou,730050

The algorithm of NURBS curve fitting was put forward based on least square method,and the NURBS interpolation technology based on arc length parameter compensation.By the analyses of characteristics of the free surface interpolation algorithm of modern CNC system,NURBS curve fitted with least square method could achieve a smooth tool path and reconstruct designed outline curves to some extents.The NURBS method of parameter compensation,which used interpolation parameters to be temporary interpolation points obtained by the Taylor expansion method,was applied to ensure that the speed rate fluctuations could be decreased effectively,and that the speed was controlled within the ideal range,and that the process precision was further improved,and that the vibration of machine was reduced.The simulation results show that the algorithm is simple and efficient,and easy to be implemented,which can satisfy the demands of modern CNC system.

CNC;NURBS curve;least square method;parameter compensation

2014-07-24

TH166;TP65< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.12.012

楊萍,女,1964年生。蘭州理工大學機電工程學院教授。研究方向為CAD/CAM一體化、虛擬設計、工業機器人。已發表論文60余篇。楊明泰，男，1986年生。蘭州理工大學機電工程學院碩士研究生。張陽陽,男,1988年生。蘭州理工大學機電工程學院碩士研究生。