智能輪式機器人離散模糊自適應PID控制研究
張文君,盛維濤,袁宇鵬,李曉龍
(1. 四川工程職業技術學院,德陽 618000;2. 重慶大學 自動化學院,重慶 400044)
0 引言
移動機器人是一種在復雜環境下工作的,具有自行組織、自主運行、自主規劃的智能機器人[1],它融合了計算機技術、信息技術、通信技術、微電子技術和機器人技術等。智能輪式機器人是一種典型的移動機器人,廣泛運用于倉庫運輸、博物館向導[2]、變電站巡檢等場合[3]。
智能輪式機器人運動系統的實時、有效控制是智能輪式機器人執行任務的必要保障。PID控制是過程控制中最通用的控制方法,PID控制器及其改進型控制器是工業過程控制等領域最常見的控制器[4]。然而,由于智能輪式機器人具有高度的非線性、強時變性的特點,常規的PID控制方法已經無法完成有效的控制的。因此,在輪式機器人運動系統的控制領域,許多專家學者致力于改進型的PID控制。D. Shen等[5]針對機器人運動控制系統,提出了一種基于李雅普諾夫的自適應PID控制方法。丁度坤等[6]針對噴涂機器人提出了一種基于最小二乘法的自適應PID控制方法。李冬等[7]將PID與神經網絡技術結合,提出BP神經網絡PID控制器來處理機器人運動控制問題。
當今社會的控制領域中,幾乎所有的控制器均是采用數字控制技術,因此離散式控制方法在現代控制領域凸顯了十分重要的地位。本文在常規連續式PID基礎上,采用了一種離散式的PID控制器,并且結合了操作簡單、易于實現的模糊推理理論。在分析了智能輪式機器人運動系統的動力學模型的基礎上,推導出了運動控制系統的連續式和離散式系統控制模型,進而提出了離散式模糊自適應PID控制算法,并通過MATLAB仿真驗證了控制算法的有效性。
1 智能輪式機器人動力學理論研究
本文針對的巡檢類小型三輪智能移動機器人主要可實現小型變電站巡檢、圖書館類巡視等的任務,工作環境相對平整,因此選用的是一類三輪可移動式機器人,如圖1所示。圖中AL和AR分別表示左右后輪,BL和BR分別表示帶動左右后輪轉動的電機,C為前輪。移動機器人的驅動來源是兩后輪差速驅動,前輪為萬向輪僅起到輔助導向以及平衡本體的功能。

圖1 輪式移動機器人運動轉向系統結構示意圖
智能輪式移動機器人的運動轉向系統可表征為典型的復雜系統,具有非線性、強時變性的特點。因此,為建立智能輪式移動機器人運動轉向系統的動力學模型,本文提出了如下假設:1)車輪與地位運行形式僅為純滾動,無打滑行為;2)左右后輪保持精確同心;3)不考慮道路粗糙度以及障礙物對于機器人運動的影響。
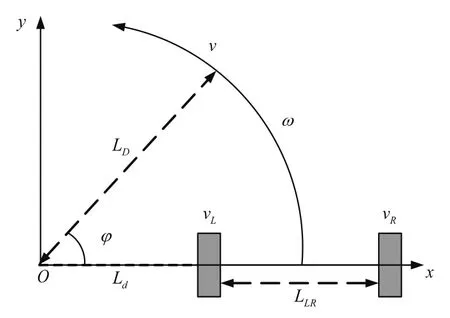
圖2 后驅左右輪運動示意圖
地面運行時,輪式移動機器人的運動行為可分解為直線、旋轉兩類。兩類運動行為的時空疊加組合可表現為移動機器人地面空間上的直線運動、曲線運動、原地轉彎等行為。智能輪式移動機器人的運動行為示意圖如圖2所示。在笛卡爾坐標系下,智能輪式移動機器人的運動方程可表示為:

其中x,y和φ分別表示移動機器人左右后輪的質心坐標與角度,移動機器人的位姿狀態為,v為直線運動速度,ω為旋轉角速度。
本文的智能移動機器人的后輪運動工作在差速驅動模式下,可通過以機器人左右輪不同的速度實現各類基本運動行為,此種控制方式簡單,易于操作。令左右后輪的半徑為DL、DR,則左右輪的速度可表示為:

其中vL和vR為左右輪的運動速度,nL和nR分別表示左右輪的編碼脈沖數量,Ce為輪子速度系數,tL和tR為左右輪旋轉一周的時間。
若假設輪式移動機器人滿足剛體運動規律,根據車輪的物理約束條件可建立如下速度方程:
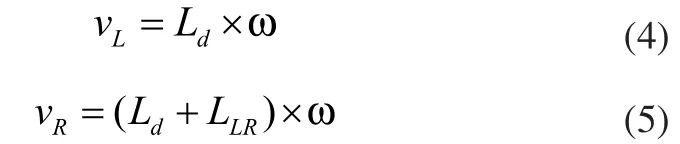
其中Ld為左輪與原點的直線距離,LLR為左右輪之間的直線距離。因此,由式(2)和式(3)可以推導出左右輪中心點的運動速度和旋轉速度:

綜上所述,輪式移動機器人運動過程中,通過實時控制左驅動輪和右驅動輪的速度即可調節輪式移動機器人的運動速度與旋轉角度,進而實現預期的移動機器人位置、姿態與空間定位。對于輪式移動機器人的控制而言,通常均是通過數字控制的方式實現差速驅動轉向,對于驅動輪轉速變換進行數字式離散化高速運算,進而滿足連續調節、精確控制的效果。
2 輪式機器人運動系統的控制模型
通過上文中的動力學理論分析,智能輪式機器人的運動系統的連續式傳遞函數可表示為[7]:

其中0.2α=,18δ=。為進行數字式仿真,同時為了保證系統離散脈沖函數不出現兩個及以上的假性零點,本文以采樣時間Ts=0.1s將以上連續式傳遞函數通過輸入端的零階保持器(ZOH)改寫成離散形式的脈沖傳遞函數:
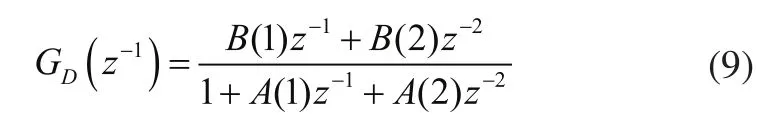
3 輪式機器人運動系統的離散式模糊自適應PID控制器
本節闡述了模糊自適應數字PID控制器的原理,并描述了詳細的設計過程。
3.1 模糊自適應數字PID控制器原理
常規數字式PID控制器控制算法可表示為:
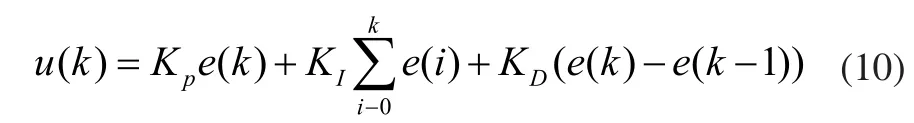
因此,可導出常規增量式數字PID控制算法表達式:
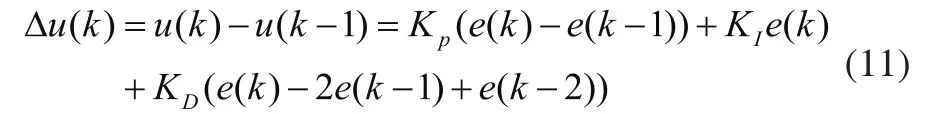
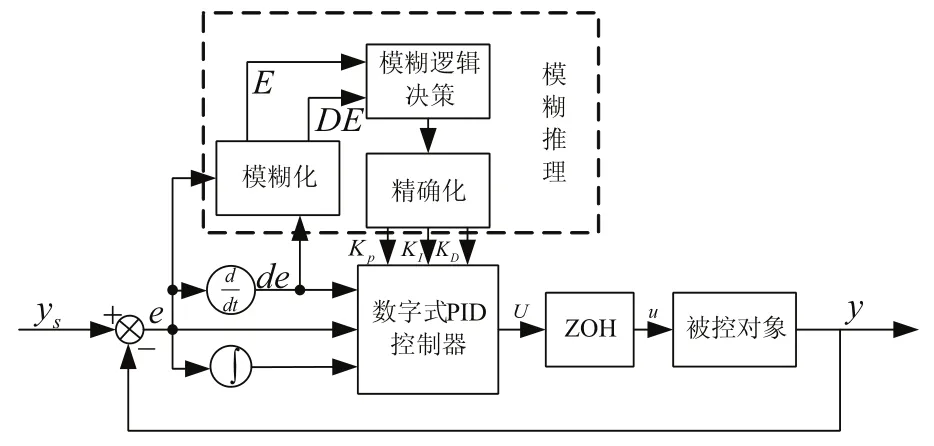
圖3 離散模糊自適應PID控制器原理圖
模糊自適應數字PID控制器原理如圖3所示。模糊自適應數字PID算法結合了模糊推理理論與PID控制算法的特點,能夠根據相關先驗知識,實時在線辨識出數字式PID控制器參數,從而提升控制器的自適應的能力。圖3中首先將誤差e與誤差導數de經過模糊推理的模糊化處理,得到E和DE。然后基于模糊規則庫進行模糊推理決策推理出數字式PID參數并再利用逆模糊化處理進而得到數字式PID控制的實時控制參數KP、KI和KD,從而實現控制輸出的自適應調節。
3.2 模糊自適應數字PID控制器設計
針對實際對象的模糊推理控制器的設計過程的關鍵在于基于設計人員的先驗知識和實際經驗,建立模糊推理規則表。為在線調節PID控制器的三個參數,通過分析pKΔ、IKΔ和DKΔ對于機器人運動控制系統輸出的影響及專家經驗,利用IF-THEN語言,獲取pKΔ、IKΔ和DKΔ參數的模糊規則,本文的模糊自適應數字PID控制器參數的模糊規則表如表1~表3所示[8]。

表1 PID參數中pKΔ的模糊推理規則表
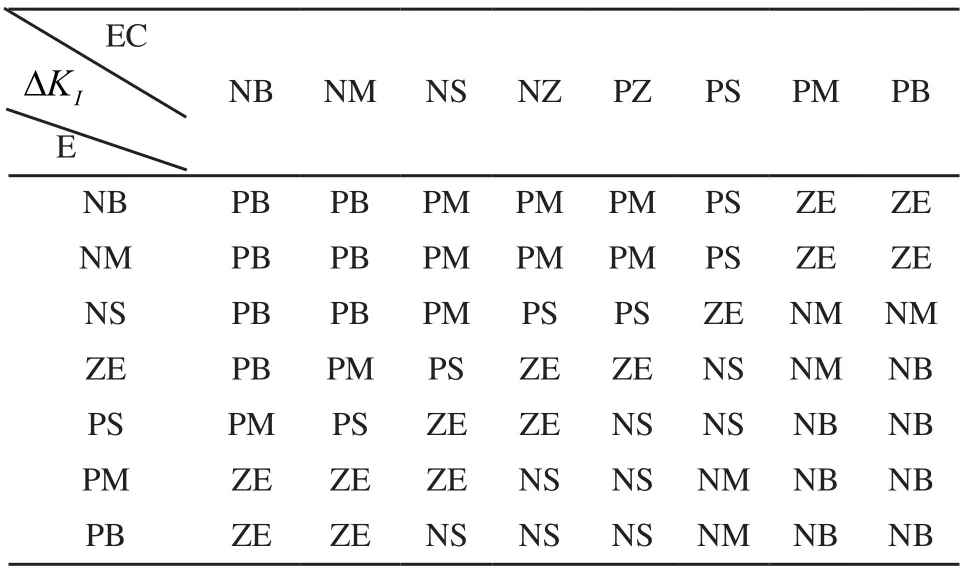
表2 PID參數中IKΔ的模糊推理規則表

表3 PID參數中DKΔ的模糊推理規則表
表中NB、NM、NS、NZ、ZE、PE、PS、PM和PB分別表示“負大(Negative big)”、“負中(Negative middle)”、“負小(Negative small)”、“負零(Negative zero)”、“零(Zero)”、“正零(Positive zero)”、“正小(Positive small)”、“正中(Positive middle)”和“正大(Positive big)”[9]。智能輪式移動機器人運動系統輸出的誤差模糊子集為E={NB,NM,NS,ZE,PS,PM,PB},系統輸出的誤差導數(即誤差增量)的模糊子集為DE={NB,NM,NS,NZ,PZ,PS,PM,PB}。
若PID參數KP、KI、KD和系統誤差E、系統誤差增量DE均服從正態分布,于是可分別建立各自的模糊子集隸屬度函數,并利用模糊子集隸屬度的賦值表與各個參數的模糊控制模型,進而可以制定PID參數KP、KI、KD的模糊推理表。數字式PID參數KP、KI、KD的增量式迭代過程可表示為:
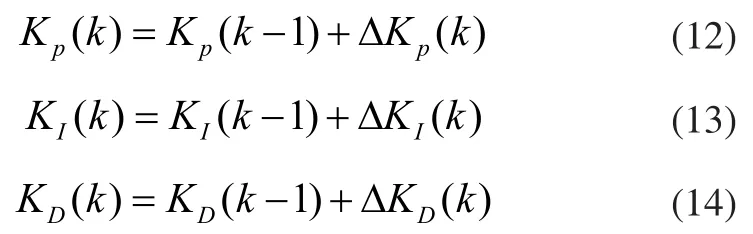
4 仿真結果與分析
本節首先基于輪式機器人運動系統的控制模型分析了運動系統的動態特性,然后對于基于離散模糊自適應PID的輪式機器人運動系統的動態過程進行了仿真分析。
4.1 輪式機器人運動系統控制模型特性分析
在MATLAB(R2011b, MathWorks)平臺上對于運動系統的控制模型進行仿真,控制模型的階躍信號仿真圖如圖4所示。從圖中可以看出,輪式機器人運動系統具有高度的非線性和強時變性。
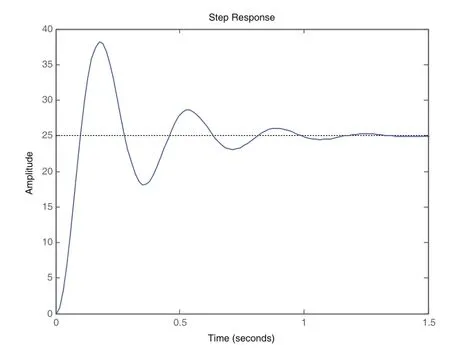
圖4 智能輪式機器人運動系統控制模型的系統響應
4.2 基于離散模糊自適應PID的輪式機器人運動系統的仿真分析
為驗證所設計離散模糊自適應PID控制器的有效性,本文針對智能輪式機器人的動力學模型在MATLAB(R2011b, MathWorks)平臺進行仿真研究。仿真過程中,模糊自適應數字式PID控制器的控制流程如圖5所示。

圖5 離散模糊自適應PID控制器的控制流程圖
基于模糊自適應數字式PID控制器的智能輪式機器人運動系統的仿真如圖6所示。仿真過程系統的參考信號采用階躍信號,由圖6可知模糊自適應PID控制器和常規PID控制器的超調量分別為28%和67.5%,調節時間分別為35s和53s,峰值時間分別為95s和120s。此外,模糊自適應PID控制器僅有一個波峰即達到穩定,而常規PID控制器經過多次波峰才趨于穩定,調節時間過長,所以模糊自適應PID的控制性能明顯優于常規PID控制器的控制效果。

圖6 智能輪式機器人運動系統的仿真圖
5 結束語
本文基于智能輪式機器人的動力學基本理論,建立了輪式機器人運動系統的動力學模型,并闡述了輪式機器人運動系統的連續與離散兩種控制模型。在此基礎上,本文通過將模糊推理理論與離散式PID控制算法相結合的方法,綜合了二者的優勢,提出了離散式模糊自適應PID控制器。最后,本文基于MATLAB平臺,將離散式模糊自適應PID控制器與常規離散式PID控制器運用于輪式機器人運動系統的離散控制模型上進行了仿真對比,仿真結果顯示,離散式模糊自適應PID控制器的控制性能明顯優于常規離散式PID控制器。今后的研究中,在研究單個輪式機器人運動系統控制方法的基礎上,將進一步研究多機器人的編隊控制問題。
[1] S. János, I. Matijevics, Implementation of Potential Field Method for Mobile Robot Navigation in Greenhouse Environment with WSN Support[A].in 2010 8th International Symposium on Intelligent Systems and Informatics (SISY),[C].2010,319-323.
[2] A. C. ?, I.Macaluso, The perception loop in CiceRobot, a museum guide robot[J].Neurocomputing,2009,72(4-6):760-766.
[3] F. Liu, S. Liang, X. Xian, H. Bi, Optimal path planning for mobile robot in consideration of road attributes[J].ICIC Express Letters,2012,6(1):281-287.
[4] 王偉,張晶濤,柴天佑.PID參數先進整定方法綜述[J].自動化學報,2000,26(3):347-355.
[5] 陸磊,模糊PID控制在輪式機器人上的應用[J].微型電腦應用,2010,26(12):31-33.
[6] 丁度坤,鄒焱飚,張鐵,謝存禧.噴涂機器人關節的PID自適應模型[J].華南理工大學學報(自然科學版),2009,37(4):90-94.
[7] 李冬,周利坤.清洗機器人自適應PID控制研究[J].計算機仿真,2012,29(12):239-242.
[8] 宋新甫,梁波.基于模糊自適應PID的風力發電系統變槳距控制[J].電力系統保護與控制,2009,37(16):50-58.
[9] 陳剛,張為公.基于模糊自適應PID的汽車駕駛機器人的車速控制[J].汽車工程,2012,34(6):511-516.

