重視基本活動經驗 培養學生合情推理

錢長國

摘 要：基本活動經驗是指學生的已有知識經驗和生活經驗。小學數學教學中教師要從學生的基本活動經驗入手，創設情境，讓學生通過觀察、猜想、驗證、歸納、類比、聯想等方法，培養學生的合情推理能力。

關鍵詞：基本活動經驗；合情推理

中圖分類號：G623.5 文獻標識碼：A 文章編號：1992-7711（2015）18-073-2

《小學數學課程標準（實驗稿）》在課程的具體目標中指出：“培養和發展學生的合情推理能力。”合情推理最早是美籍數學家波利亞在30年代提出的概念，它是指“觀察、歸納、類比、實驗、猜測、矯正和調控等日常生活中積累的知識、經驗，經過非演繹（非完全演繹）的思維而得到的合乎情理、理想化的一種推理方法。

波利亞說：“有效地應用合情推理是一種實際技能”。在小學數學教學中，教師要從學生的基本活動經驗入手，培養學生的合情推理能力。

一、從學生生活經驗入手，溝通算理聯想推理

蘇教版教材第7冊中教學乘除混合運算時，有這樣一道題，讓學生計算56÷4÷7與56÷（4×7）的結果進行比較。教師讓學生先猜想，然后通過計算得出：56÷4÷7=2，56÷（4×7）=56÷28=2。所以推理出56÷4÷7=56÷（4×7）。教學到此程度，不少教師都會讓學生記住：在三個數連除算式中可以把后兩個數用小括號括起來，括號里除號變乘號。它們的結果是一樣的。事實上，我們可以根據學生已有的知識經驗和生活經驗進一步幫助學生理清算理，明了意義，更有助于學生理解、記憶。教師可以通過編生活中的應用題來理解算理。如：學校為了倡導足球文化，把56只足球平均分給三至六年級4個年級，每個年級7個班，平均每班分得足球多少只？學生有兩種列式理由，一是根據數量關系式先求出平均每個年級分得足球多少只？（56÷4），再求平均每班分得足球多少只？（56÷4÷7）。第二種求法是先求出三至六年級共有幾個班？（4×7），再求平均每班分得足球多少只？56÷（4×7）。最后讓學生比較算理，思考所求問題，進一步得出：56÷4÷7與56÷（4×7）都是求平均每班分得足球多少只，它們是相等的。

二、借助線段圖讓學生觀察，直觀推理

小學數學教學中，巧妙借助線段圖教學，可以化難為易，變抽象為具體，可以有效地幫助學生合情推理。

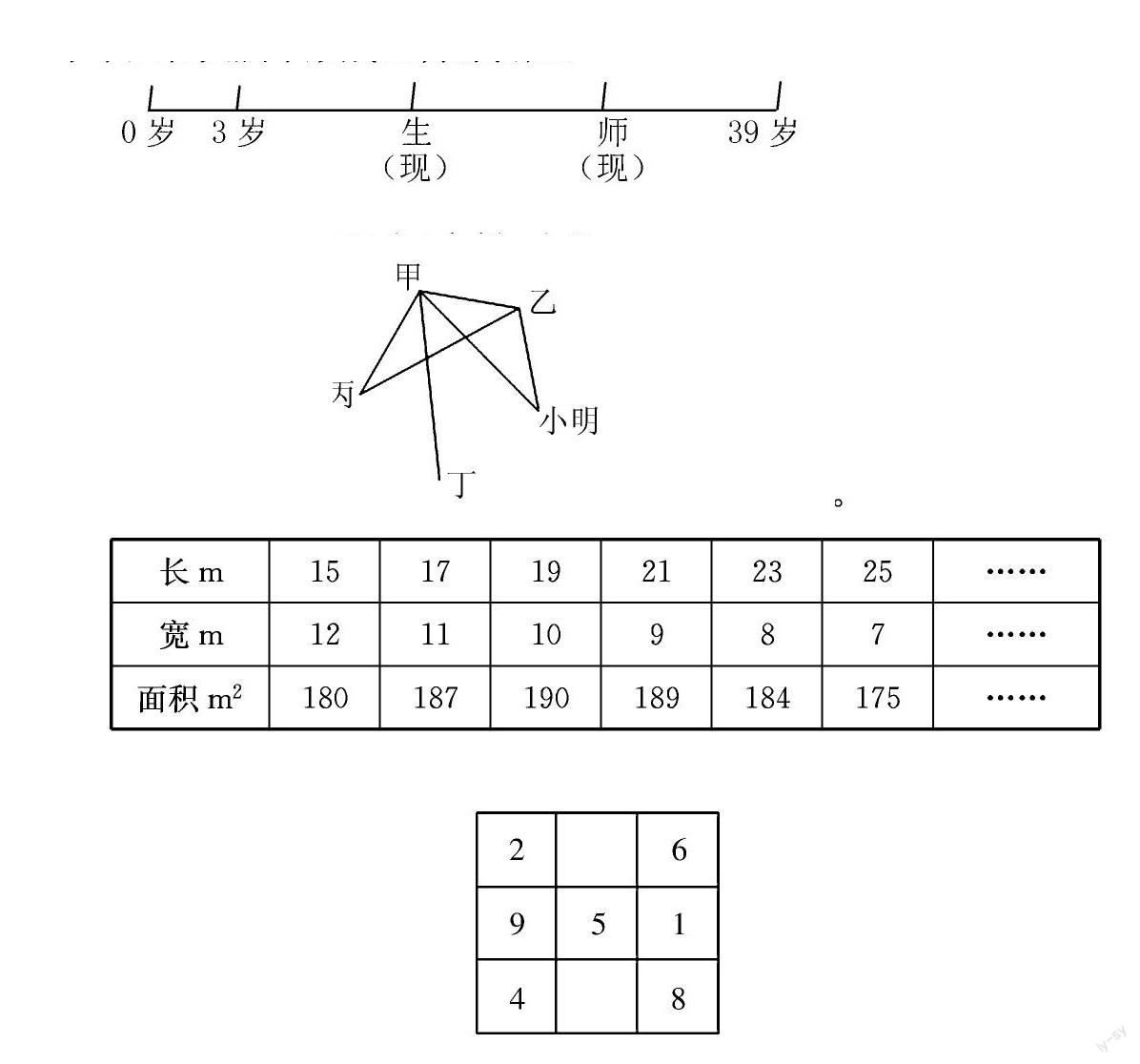
如：“學生問老師多少歲，老師說：‘當我像你這么大時，你剛3歲。當你像我這么大時，我已經39歲。那么，老師今年多少歲？”

這個問題，如果不借助線段圖來直觀觀察，多數學生很難理解題目中隱藏的隱蔽條件，從而很難去推理。如果用線段圖來表示，便于學生在頭腦中形成正確的表征。

從0歲開始畫起，學生3歲，老師是學生現在的年齡。中間存在著一個年齡差。而今年老師與學生的年齡也同樣存在著相同的年齡差。當學生長到老師的年齡時，老師已39歲了。又相隔一段年齡差。也就是說，39-3=36歲實際上就是師生之間年齡差的3倍，所以年齡差應該是（39-3）÷3=12歲。這樣可以推理出老師今年的年齡就是39-12=27歲。

又如：“甲、乙、丙、丁和小明一共五人進行羽毛球比賽，每兩人比賽一場，比賽中途做了一次統計：甲比了4場，乙比了3場，丙比了2場，丁比了1場。這時小明比賽了幾場？”這道題如果老師不借助描點畫圖連線，學生在理解上就會無從下手，丈二和尚摸不著頭腦。根據題意可以用點來代替甲、乙、丙、丁、小明5人，用連線法畫圖如下：

甲比了4場，說明甲與其他4人分別比賽了1場。根據丁比了1場，說明丁只能跟甲比一場，其余都沒有比。根據乙比了3場，可知乙與甲、丙、小明各比了1場。丙比了2場，很明顯從圖中可以看出丙與甲、乙各比賽了1場。由圖可以推理出，此時小明只與甲、乙各比了1場，即小明在中途統計時只比賽了2場。

三、通過枚舉，合情推理

小學數學教學中，一一枚舉，可以清楚地看出一些數量前后變化規律，有助于問題的解決。如“張大伯用一根39米長的草繩靠一面墻圍成了一個長方形籬笆，長與寬都取整米數，當長=（ ）米，寬=（ ）米時，圍成的長方形籬笆面積最大？

教師可啟發學生通過列表枚舉去自主探究。

長m151719212325……

寬m121110987……

面積m2180187190189184175……

通過列表，可以看出，當長等于15米，寬等于12米時，長方形面積是180平方米。當長等于19米，寬等于10米時，長方形籬笆的面積最大是190平方米。當長分別為21米、23米、25米，長方形面積由189平方米逐步減少到175平方米。

有些題目，在枚舉時，要適時地進行調控、矯正、推理要合乎情理。

如：“將“1～9”九個數分別填入下面的九宮格中，使九宮格中橫排、豎排、對角線上的三個數之和分別都相等。”

要把“1～9”九個數填入右圖中，使橫、豎、對角線上的三個數之和都相等。可以先求出1+2+3+……+9的和是45，每一排之和是45÷3=15。我們可以來枚舉一下，1～9九個數哪三個數相加的和等于15呢？

①枚舉如下：1+9+5=15 2+8+5=15 3+7+5=15 4+6+5=15，與5相加的另外兩個數只有這四組。由此可以推理出九宮格中中間一個數是5。也只有5在中間才能保證四種情況即橫、豎排及兩條對角線上三個數之和都等于15。

②枚舉：9+2+4=15 8+1+6=15 8+3+4=15 7+6+2=15；

通過觀察思考：可以知道以上8組數中，與5相加的數有4組，與8相的數有3組，與6相加的數也有3組；分別是A組2+8+5=15，8+1+6=15，8+3+4=15；B組4+6+5=15，7+6+2=15，8+1+6=15。這樣我們可以大膽推斷8與6都在九宮格的四角上。只有在角上，才能保證橫排、豎排及一條對角成上的三個數之和都等于15。但是8與6又不能在一條對角線的兩個角上，因為這樣6+8+5=17，和就不等于15了，不符合要求。為此，8與6在一排上的兩個角上，中間只能是1。這樣一推理，就很快推理出8、5、2一組，6、5、4一組，1、5、9一組。填起來就很容易了。顯然，列舉時教師要引導學生不重復，不遺漏，重視培養學生有序列舉的習慣。

四、建立模型，猜測推理

數學習題中，有些題要思考路徑，讓學生在頭腦中先建立模型，再順藤摸瓜，猜測推理。

如：在等號左邊填上合適的運算符號和括號，使計算結果等于右邊的數。

（一）3 3 3 3=1， （二）3 3 3 3=2。

我們在解這類題目時，可以從結果入手，通過建立模型來解決問題。

先看“3 3 3 3=1”，要使4個3的運算結果等于1，可以這樣想，3與1之間有什么關系？很顯然：3-2=1，這就是模型。我們只需要將最前面的3留下，剩下的3個3湊成2就行了。即：3-（3+3）÷3=1。當然也可以建立模型“0+1=1”，即3-3+3÷3=1。也可以建立模型“1×1=1”，即（3÷3）×（3÷3）=1。再來看“3 3 3 3=2”，可以建立模型1+1=2，即3÷3+3÷3=2；也可以建立模型5-3=2，但是前三個3湊不成5，這樣的模型在實踐探究中需要調整。

五、演示歸納，類比推理

杜威說：“經驗就是教育的創造或改組。”數學教學中對學生的思維訓練有時可以先借助實物演示，然后根據學生已有的認知水平與生活經驗歸納、類比，讓學生合情推理。

如教學：“有一個大正方體，在它的表面涂上顏色，然后將大正方體切割成棱長是1厘米的小正方體，已知兩面都涂色的小正方體共有60個，求原大正方體的體積是多少立方厘米？”

教者可先讓學生觀察實物圖，然后操作演示。啟發學生思考這樣一個數學問題，看“兩面涂色的小正方體在大正方體的什么位置上？”學生觀察得出：兩面涂色的小正方體都在大正方體的12條棱上。但每條棱的兩端兩個小正方體都是三面涂色，不符合要求。通過觀察，可以得出大正方體每條棱上有5個兩面涂色的小正方體。那么可以推理大正方體12條棱上共有兩面涂色的小正方體個數是5×12=60個。這與題目中所給的已知條件完全相同。通過歸納、類比，我們不難得出：大正方體12條棱的長度都相等，每條棱上兩面涂色的小正方體個數是相同的，就是60÷12=5（個）。由于大正方體每一條棱的兩端都有一個三面涂色的小正方體，由此可以推理出大正方體的一條棱上就由5+2=7個小正方體組成，即大正方體的棱長就是7×1=1（厘米）。這樣大正方體的體積就是73=343立方厘米。

當然，合情推理在數學教學中它不是孤立存在的，有時與演繹推理、邏輯推理綜合應用。合情推理只有植根于學生基本活動經驗這塊沃土，才能開出更加艷麗的花朵，結出豐碩的果實。