廣義猶豫正態模糊信息集成及其多屬性群決策

馬慶功

常州大學懷德學院，江蘇常州213016

廣義猶豫正態模糊信息集成及其多屬性群決策

馬慶功

常州大學懷德學院，江蘇常州213016

定義了猶豫正態模糊元及其運算法則、得分函數、Euclidean距離等概念；提出了廣義猶豫正態模糊有序加權平均算子，并研究其性質，該算子不僅盡可能多地保留決策者的偏好信息，還可依據決策者的主觀意愿選擇不同的參數和屬性權重，使得決策結果達到決策者的期望值；緊接著對屬性權重和算子參數賦予不同的數值，獲取廣義猶豫正態模糊有序加權平均算子的若干種特殊算子，并探討兩個常用算子的大小關系；針對屬性權重完全未知的多屬性群決策問題，構建一種基于廣義猶豫正態模糊有序加權平均算子的群決策方法。該方法利用同一屬性下所有方案屬性值間的距離求得最優權重，然后將同一方案下各屬性值集結成為綜合屬性值，進而得到方案優劣排序。通過實例分析說明該方法的可行性和有效性。

猶豫正態模糊元；多屬性群決策；信息集成算子；計算機網絡系統

在管理決策分析中，由于社會的迅速發展，人們認知問題的思維和事物本身的復雜性、模糊性和不確定性，使得決策者在進行評判時，常常無法給出精確的數值。

自1965年Zadeh首先提出模糊集［1］概念之后，模糊集理論成為處理模糊信息的有效工具，并廣泛地應用于風險投資、經濟管理、模式識別、醫療診斷、控制理論等領域。之后，人們提出了模糊集的幾種廣義形式，包括：區間模糊集［2］、直覺模糊集［3］、區間直覺模糊集［4］、猶豫模糊集［5］、區間猶豫模糊集［6-7］、對偶猶豫模糊集［8］等等。Xu和Chen［9］提出了區間直覺模糊算數平均算子，并且將其應用于區間直覺模糊環境下的多屬性決策過程中。徐澤水［10］研究了在直覺模糊信息環境下的各種集結算子，包括有序加權平均算子、有序加權幾何算子、誘導有序加權平均算子及誘導有序加權幾何算子等。Wei［11］在區間猶豫模糊環境下，提出了各種信息集成算子，并討論了這些算子的性質。基于猶豫模糊集和直覺模糊集間的關系，Xia和Xu［12］提出了猶豫模糊信息集成算子。王堅強和李康健［13］構建了一種基于直覺正態模糊信息集結算子的決策方法，并將其應用于發動機零部件制造公司選擇供應商的案例中。

隨著社會的飛速發展，人們的生活中有大量的自然現象和社會現象是服從正態分布的［14］，并且運用正態模糊數表述決策信息可以更加客觀準確地描述和反映現實中的數據信息。一方面，現有的模糊數的概念的論域大多是離散的，題型模糊數定義在某個確定的區間；另一方面，猶豫模糊信息將所有決策者的決策信息全面進行保留，能夠防止因決策信息丟失而導致決策結果不準確的后果［15］。因此，研究定義在整個連續區間上的猶豫模糊信息及其信息集成方式具有十分重要的理論價值和現實意義。本文首先定義了猶豫正態模糊元的相關概念，然后提出了廣義猶豫正態模糊信息集成算子，最后在猶豫正態環境下，基于提出的信息集成算子構建了一種新的多屬性群決策方法，并以政府部門對計算機網絡系統的選擇為例，說明所提方法的有效性。

1　基本概念

本章首先回顧了正態模糊數的概念，然后給出猶豫正態模糊元的定義，最后提出猶豫正態元的運算法則、得分函數以及大小比較方法。

定義1.1［14］在實數域R上，稱隸屬函數為μA（x）=的模糊數A為正態模糊數，記為A=（a，σ）。令Ω為全體正態模糊數的集合。設Ai=（ai，σi）（i=1，2）∈Ω，則它們之間的距離公式［14］為：

為了方便計算，記H?為全體HNFE組成的集合。

與猶豫模糊元相比，HNFE增加了一個新的正態模糊數（a，σ），這使得其論域由離散擴展到整個連續區間，這樣隸屬度不再只是相對于一個模糊的概念，而是相對于該正態模糊數，能更加準確地反映決策信息，同時HNFE能全面地表達決策者們的不同決策信息，應用范圍更加廣泛。

接下來，將提出HNFE的運算法則，并研究它們間的運算性質。

容易證明，上述定義的猶豫正態模糊運算法則滿足以下性質：

下面，將討論HNFE的排序方法。先給出如下概念：

當HNFE退化為正態模糊數時，即h1=h2=｛1｝，則有，此時HNFE的距離公式也退化為正態模糊數的距離公式。

2　廣義猶豫正態模糊有序加權平均算子

基于上一章定義的猶豫正態模糊運算法則，本章將提出一種廣義猶豫正態模糊信息集成算子，并研究其優良性質，包括：單調性、有界性、冪等性、置換不變性。

證明（1）先證明等式（6）成立。首先運用數學歸納法證明對于所有的正整數n，如下等式成立：

假設當n=k時，等式（7）成立，即

當n=k+1時，依據定義1.3，有

即當n=k+1時，等式（7）成立。因此，對于所有的正整數n，等式（7）成立。

由定義1.3的運算，則有

（2）接下來，需證明GHNFOWA算子的集成結果仍是一個HNFE，關鍵是證明對?γ1∈h1，γ2∈h2，…，γn∈hn，有

事實上，因為γ1，γ2，…，γn∈［0，1］，那么對于?j=

綜上，定理2.1成立。

（4）置換不變性：設A?φ（1），A?φ（2），…，A?φ（n）是A?1，A?2，…，A?n的任意一個置換，則有

3　GHNFOWA算子的幾種常見形式

首先依據權重向量w=（w1，w2，…，wn）T和參數λ取不同的數值，得到GHNFOWA算子的若干種特殊形式，然后探究其中兩種常見算子的大小關系。

Case 1：權重向量w=（w1，w2，…，wn）T取不同的數值。

①若w=（1，0，…，0）T，GHNFOWA算子將變為猶豫正態模糊極大（HNF-MAX）算子，即：

②若w=（0，0，…，1）T，GHNFOWA算子將變為猶豫正態模糊極小（HNF-MIN）算子，即：

Case 2：參數λ取不同的數值。

如果λ=1時，GHNFOWA算子將會退化為猶豫正態模糊有序加權算術平均（HNFOWAA）算子：

如果λ→0時，GHNFOWA算子將會退化為猶豫正態模糊有序加權幾何平均（HNFOWGA）算子：

接下來將探究這兩個常用的算子，即猶豫正態模糊有序加權算術平均（HNFOWAA）算子和猶豫正態模糊有序加權幾何平均（HNFOWGA）算子之間的大小關系，為此，先引入以下引理：

引理3.1［15］假設xj＞0，λj≥0，j=1，2，…，n，并且，則有。當且僅當x1=x2=…=xn時，等號成立。

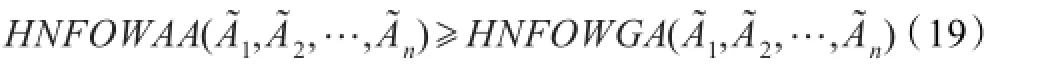
證明為了方便計算，令

依據定義1.5，有：因此結論成立。

定理3.1表明運用HNFOWAA算子得到的猶豫正態模糊元不小于運用HNFOWGA算子得到的猶豫正態模糊元。

4　基于GHNFOWA算子的多屬性群決策方法

基于GHNFOWA算子提出一種新的多屬性群決策方法，其中的屬性權重為實數，屬性值以HNFE的形式表示。

考慮猶豫正態模糊多屬性群決策問題，假設有m個可行方案Y1，Y2，…，Ym，伴隨每個方案的屬性集合為C=｛C1，C2，…，Cn｝，關聯權重向量w=（w1，w2，…，wn）T完全未知，其滿足。在決策過程中，每個決策者都給出可行方案Yi在屬性Cj下的偏好信息。由于每個決策者提供的偏好信息不一定相同，因此這些偏好信息就構成了可行方案Yi在屬性Cj下的HNFE，則所有決策者提供的可行方案集在屬性集下的決策偏好信息可構成一個猶豫正態模糊信息決策矩陣。

針對上述問題，給出基于廣義猶豫正態模糊信息集成的多屬性群決策方法，具體步驟如下：

步驟1標準化處理

①當Cj為效益型屬性時，，其中；

②當Cj為成本型屬性時，，其中。

步驟2確定屬性權重

在進行多屬性決策時，如果某一屬性下的所有方案屬性信息差異越小，則說明該屬性能夠給決策者提供的決策信息量就越少，于是在決策過程中的重要性就越低，則應該賦予這個屬性的權重就越小。反之，若所有方案在某一屬性下的屬性值有明顯的差異，則表明該屬性能夠給決策者提供較多的決策信息，那么該屬性在決策過程中就越重要，則應賦予其較大的權重。因此若屬性Cj（j=1，2，…，n）的權重信息完全未知，則可通過以下方法確定權重wj：

步驟3集結可行方案的綜合屬性值

依據標準決策矩陣R?和提出的GHNFOWA算子，計算每個可行方案Yi（i=1，2，…，m）的綜合屬性值R?i（i=1，2，…，m），即

步驟4計算均值得分函數和標準差得分函數

步驟5可行方案優劣排序

運用定義1.5中的排序方法，對可行方案Yi（i=1，2，…，m）進行優劣排序，并選擇出最優的決策方案。

表1　決策者提供的猶豫正態模糊決策矩陣?=）4×4

表1　決策者提供的猶豫正態模糊決策矩陣?=）4×4

C1 C2 C3 C4 Y1 Y2Y3 Y4＜（7.1，2.1），｛0.45，0.65｝＞＜（4.1，3.0），｛0.32，0.50｝＞＜（8.6，1.9），｛0.55，0.69｝＞＜（9.2，1.2），｛0.54，0.65｝＞＜（4.1，1.8），｛0.35，0.57｝＞＜（6.8，1.0），｛0.15，0.28｝＞＜（6.2，2.1），｛0.60，0.85｝＞＜（7.1，2.4），｛0.40，0.72｝＞＜（5.7，1.7），｛0.45，0.63｝＞＜（7.1，3.0），｛0.39，0.64｝＞＜（5.4，2.4），｛0.62，0.73｝＞＜（6.1，2.0），｛0.40，0.52｝＞＜（4.8，0.6），｛0.59，0.77｝＞＜（5.1，1.7），｛0.70，0.81｝＞＜（6.2，2.5），｛0.65，0.72｝＞＜（7.1，1.3），｛0.49，0.64｝＞

5　案例分析

考慮一個計算機網絡系統選擇問題。某政府機關欲通過計算機網絡和通信等現代信息技術手段，實現政府組織結構和工作流程的優化重組，超越時間、空間和部門分隔的限制，建成一個精簡、高效、廉潔、公平的政府運作模式，以便全方位地向社會提供優質、規范、透明、符合國際水準的管理與服務。該政府采購部門現將從現有4套計算機網絡系統Yi（i=1，2，3，4）中選擇一套計算機網絡系統進行安裝。為了選擇一套性能最優的計算機網絡系統，該政府采購部門將對四套系統分別在以下四個性能指標下進行綜合評估，即C1網絡速率；C2系統利用率；C3帶寬；C4硬件設施，最終選擇性能一套最優的計算機網絡系統。為了保證決策評估的客觀性和權威性，該政府采購部門邀請了不同領域的專家，依據自身的專業知識和實際經驗，并結合四套計算機網絡系統在測試過程中的表現出對這四套系統在上述4個屬性指標下進行性能滿意度測評，給出了表1所示的猶豫正態模糊決策矩陣。下面依據本文提出的猶豫正態模糊多屬性群決策方法，遴選出綜合性能最強的計算機網絡系統。

步驟1標準化處理

由于C1，C2，C3和C4都是效益型屬性，則通過標準化方法（a）對猶豫正態模糊決策矩陣D?進行處理，得到標準化決策矩陣，如表2所示。

步驟3運用GHNFOWA算子分別計算出每套計算機網絡系統Yi（i=1，2，3，4）的綜合屬性值以備選系統Y2為例，令λ=1，計算綜合屬性值為：

步驟4計算在不同參數下每套計算機網絡系統的綜合屬性值R?i（i=1，2，3，4）的均值得分函數1，2，3，4），結果見表3。

步驟5依據定義1.5，在不同的參數下對四套計算機網絡系統Yi（i=1，2，3，4）進行優劣排序，排序結果見表3。從表3可知，當參數λ取不同的數值時，排序結果基本一致，且綜合性能最優的計算機網絡系統均為Y3。

為了說明本文提出群決策方法優良性能，將本文的決策方法與文獻［12］中的決策方法進行對比分析。依據文獻［12］中的猶豫模糊決策方法處理上述問題。

首先，構建猶豫模糊決策矩陣D=（hij）4×4，其中hij為表1中每個HNFE除去均值和標準差后的猶豫模糊元。

然后利用文獻［12］中的公式（27），將每套計算機網絡系統在各個屬性指標下的屬性值集結成為綜合屬性值hi（i=1，2，3，4）（同樣地，計算當λ→0，λ=1，λ=2，λ=5，λ=10時的綜合屬性值），由于hi由16個數值組成，因篇幅的限制，故在此省略。

接著，依據猶豫模糊元的得分函數公式，計算不同參數下每套計算機網絡系統綜合屬性值hi（i=1，2，3，4）的得分函數值s（hi）（i=1，2，3，4），見表4。

表2　標準化的猶豫正態模糊決策矩陣?=）4×4

表2　標準化的猶豫正態模糊決策矩陣?=）4×4

C1 C2 C3 C4 Y1Y2 Y3 Y4＜（0.6，0.6），｛0.45，0.65｝＞＜（1.0，0.4），｛0.32，0.50｝＞＜（0.5，0.6），｛0.55，0.69｝＞＜（0.4，1.0），｛0.54，0.65｝＞＜（0.6，0.7），｛0.35，0.57｝＞＜（0.9，0.4），｛0.15，0.28｝＞＜（0.9，0.9），｛0.60，0.85｝＞＜（1.0，1.0），｛0.40，0.72｝＞＜（0.8，0.6），｛0.41，0.63｝＞＜（1.0，1.0），｛0.39，0.64｝＞＜（0.8，0.8），｛0.62，0.73｝＞＜（0.9，0.7），｛0.48，0.52｝＞＜（0.7，0.4），｛0.59，0.77｝＞＜（0.7，0.7），｛0.70，0.81｝＞＜（0.9，1.0），｛0.65，0.72｝＞＜（1.0，0.5），｛0.49，0.64｝＞

表3　利用GHNFOWA算子計算四套計算機網絡系統的均值得分函數值和優劣排序

表4　利用GHFOWA算子計算四套計算機網絡系統的得分函數值和優劣排序

根據得分函數值的大小對這四套計算機網絡系統進行優劣排序，結果如表4所示。分析比較發現，運用本文方法得到的結果與文獻［12］中方法得到的結果一致，表明本文提出的群決策方法是可行的和有效的。但是本文提出的決策方法相對于文獻［12］中的決策方法有以下優勢：首先，正態分布廣泛存在于各種自然現象、社會現象和生產實踐活動中，運用猶豫正態模糊元表述決策信息可以更加客觀準確地反映現實中的數據信息；其次，猶豫正態隸屬函數具有高階導數連續的性質，而其他幾種模糊數都不具有這種性質［16］；再次，本文提出的決策方法使用范圍更為廣泛，由于文獻［12］中提出的幾何算子其實是本文提出的GHNFOWA算子的一種特殊形式，因此本文的決策方法實用性更強，拓展了猶豫模糊理論的應用范圍；最后，本文提出用HNFE刻畫模糊概念更能貼近人類思維，盡可能多地保留了決策者的偏好信息，并且利用本文提出的決策方法進行決策時，決策者可以依據自身的偏好和樂觀態度選擇不同的參數進行信息集成，從而使得決策過程更具有一定的靈活性，而且能有效的體現決策者的決策意愿。

6　結論

本文首先將離散空間上的猶豫模糊元推廣到連續空間，給出了HNFE及其相關概念，并且定義了猶豫正態模糊運算法則；其次，基于這些運算法則，提出了廣義猶豫正態模糊有序加權平均算子，并研究了其相關優良性質；接著給出了GHNFOWA算子的一些常用形式；針對屬性權重完全未知的猶豫正態模糊多屬性群決策問題，構建了一種基于GHNFOWA算子的決策方法。該決策方法利用HNFE間的距離確定屬性權重，再基于提出的GHNFOWA算子計算得到各方案的綜合屬性值，進而確定方案的優劣排序。最后將提出的決策方法應用于政府部門對計算機網絡系統的選擇過程中，并將本文方法與現有的決策方法進行比較分析，以驗證提出的決策方法是可行的和有效的。因此，本文的研究成果具有一定的理論價值和現實意義。

［1］Zadeh L A.Fuzzy sets［J］.Information and Control，1965，8（3）：338-356.

［2］Turksen I B.Interval valued fuzzy sets based on normal forms［J］.Fuzzy Sets and Systems，1986，20：191-210.

［3］Atanassov K T.Intuitionistic fuzzy sets［J］.Fuzzy Sets and Systems，1986，20（1）：87-96.

［4］Atanassov K，Gargov G.Interval-valued intuition-istic fuzzy sets［J］.Fuzzy Sets and Systems，1989，31：343-349.

［5］Torra V.Hesitant fuzzy sets［J］.International Journal of Intelligent Systems，2010，25：529-539.

［6］Chen N，Xu Z S，Xia M M.Interval-valued hesitant preference relations and their applications to group decision making［J］.Knowledge-Based Systems，2013，37：528-540.

［7］Chen N，Xu Z S，Xia M M.Correlation coefficients of hesitant fuzzy sets and their applications to clustering analysis［J］.Applied Mathematical Modelling，2013，37：2197-2211.

［8］Zhu B，Xu Z S，Xia M M.Dual hesitant fuzzy sets［J］. Journal of Applied Mathematics，2012，32（5）：317-386.

［9］Xu Z S，Chen J.Approach to group decision making based on interval-valued intuitionistic judgment matrices［J］.Systems Engineering-Theory and Practice，2007，27：126-133.

［10］Xu Z S，Intuitionistic fuzzy aggregation operators［J］.IEEE Transactions on Fuzzy Systems，2007，15：1179-1187.

［11］Wei G W，Zhao X F，Lin R.Some hesitant interval-valued fuzzy aggregation operators and their applications to multiple attribute decision making［J］.Knowledge-Based Systems，2013，46：43-53.

［12］Xia M M，Xu Z S.Hesitant fuzzy information aggregation in decision making［J］.International Journal of Approximate Reasoning，2011，52：395-407.

［13］王堅強，李康健.基于直覺正態模糊集結算子的多準則決策方法［J］.系統工程理論與實踐，2013，33（6）：1501-1508.

［14］Wang J，Zhou P，Li K，et al.Multi-criteria decision-making method based on normal intuitionistic fuzzy-induced generalized aggregation operator［J］.TOP，2014：1-20.

［15］Torra V，Narukawa Y.Modeling decisions：information fusion and aggregation operators［M］.［S.l.］：Springer，2007.

［16］李德毅，劉常昱.論正態云模型的普適性［J］.中國工程科學，2004，6（8）：28-34.

Generalized hesitant normal fuzzy information aggregation and their application to multi-attribute group decision making.

MA Qinggong

Changzhou University Huaide College，Changzhou，Jiangsu 213016，China

Hesitant normal fuzzy elements（HNFEs）as well as their operational laws，score functions and Euclidean distance are defined.Then，the generalized hesitant normal fuzzy ordered weighted averaging（GHNFOWA）operator is proposed and some desirable properties of the GHNFOWA operator are studied.The GHNFOWA operator not only preserves the decision maker’s preference information as much as possible，but also the values of the parameter and attribute weights can changes on the base on decision makers’attitude to make the results fix the expected values of decision makers. Furthermore，some special cases of the GHNFOWA operator are given when the weight vector and operator parameter takes different values，and the relationship between two common operators is studied.Finally，for multi-attribute decision making problems with the information of attribute weights is completely unknown，a method based on the GHNFOWA operator is investigated.The optimal weights are calculated by the distances of each alternative under an attribute，and then aggregate all the attribute values into the overall attribute values，which is followed by the ranking of the alternative. An example is given to demonstrate the developed method is practicality and effectiveness.

hesitant normal fuzzy elements；multi-attribute group decision making；information aggregation operator；computer network systems

A

O22

10.3778/j.issn.1002-8331.1503-0068

江蘇省科技支撐計劃（工業）重點項目（No.BE2013005-3）；靖江市科技局產學研項目（No.CDHJK1501001）。

馬慶功（1980—），男，碩士研究生，工程師，研究方向：電子技術及應用。E-mail：2985390216@qq.com

2015-03-08

2015-05-06

1002-8331（2015）22-0134-07

CNKI網絡優先出版：2015-05-27，http://www.cnki.net/kcms/detail/11.2127.TP.20150527.1053.001.html