特定桿長的曲柄搖桿機構設計及瞬態分析
張靈曉, 文學洙
(1.陜西鐵路工程職業技術學院機電工程系,陜西渭南714000;2.延邊大學工學院機械系,吉林延吉133002)
0 引言
現代機械設備中,平面曲柄搖桿機構已被廣泛應用。關于曲柄搖桿機構,其設計的問題一般為已知搖桿長l、搖桿擺角φ及機構的行程速比系數K,利用機構在極位時的幾何關系進行設計[1]。但是僅在以上參數已知的情況下,設計的解有無窮多個,若再添加附加幾何條件則可以準確地設計出該機構;或者在不再給幾何條件的情況下設計出最佳傳動性能的機構。然而對于確定的機構其搖桿的角位移φ、角速度ω、角加速度ε隨時間變化的情況,如果利用機械原理知識求解將十分復雜,且使用不方便。本文就針對已知曲柄桿長、搖桿桿長、搖桿擺角和從動件行程速比系數的條件下利用圖解法確定該機構的其它參數,并利用ANSYS分析軟件有限元求解法求解了搖桿的角位移、角速度、角加速度隨時間的變化情況。
1 特定桿長的曲柄搖桿機構的設計
1.1 已知曲柄AB長度l1、搖桿CD的長度l3及其擺角φ
和行程速比系數K
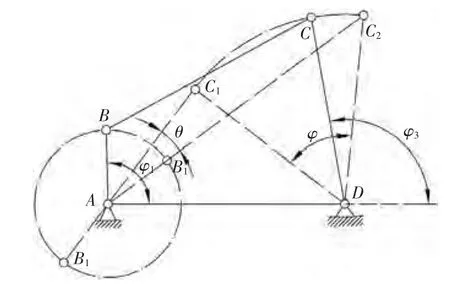
圖1 帶急回特性的曲柄搖桿機構
曲柄搖桿機構中,如圖1所示。曲柄1與連桿2重疊共線AB1和拉直共線AB2分別對應于搖桿2的兩個極限位置C1D和C2D,曲柄的固定點為A。
根據搖桿行程速比系數K,可以計算出:[2]
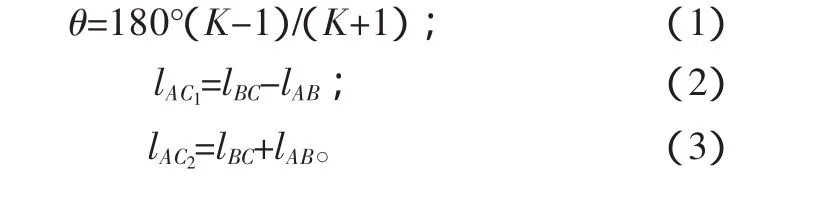
然后根據搖桿長度 l3及擺角 φ作出CD的兩極限位置C1D和C2D,以D點為原點,∠C1DC2角平分線為y軸,建立直角坐標系,如圖2所示,再作∠C2C1O1=90°-θ交 y軸于O1點,以O1點為圓心,O1C1為半徑作圓Ⅰ,交 y軸于 O2,分別延長C1D、C2D交圓于 P、Q兩點,則弧C1Q或弧C2P上的任意一點都可以是曲柄固定點A,此時,設計的解無窮多個。
由于曲柄AB的長度 l1已知,由式(2)和式(3)可得出:
lAC2-lAC1=2lAB(4)
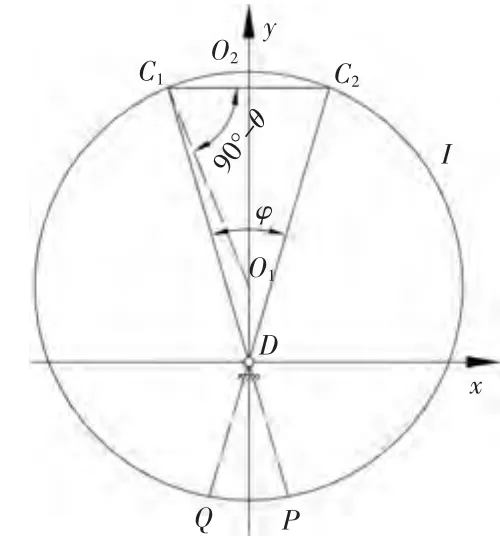
圖2 A點的軌跡
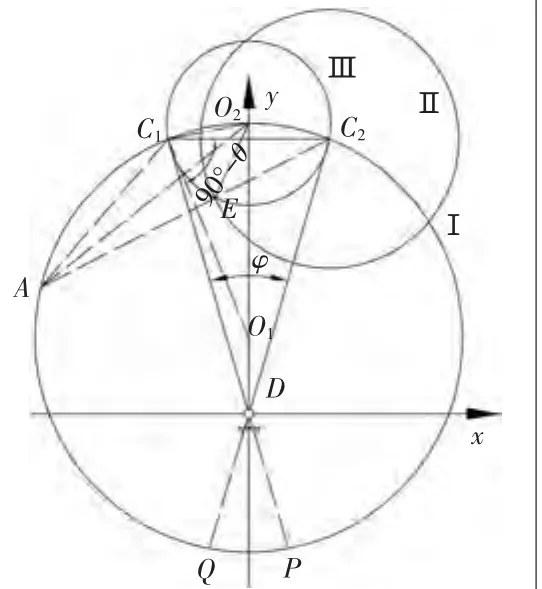
圖3 輔助線法A點位置的確定
也就是說,A點到定點C1和C2的距離之差等于一個定長,說明A點的軌跡為雙曲線。此時可以以C1、C2為焦點作雙曲線與圓Ⅰ的交點即為A點;也可以用作圓的方法找出A點,方法如下:在圖2的基礎上,以C2為圓心、以2l1為半徑作圓Ⅱ,以O2為圓心O2C1為半徑作圓Ⅲ,圓Ⅱ、圓Ⅲ交于E點,連接C2E并延長交圓Ⅰ于一點,該點即為曲柄的固定點 A[3],如圖 3 所示。
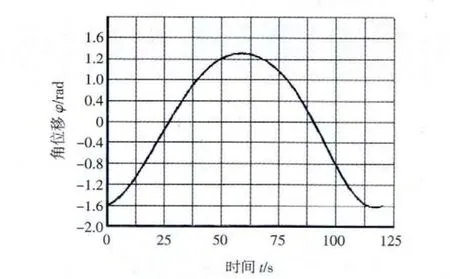
圖4 搖桿角位移-時間圖
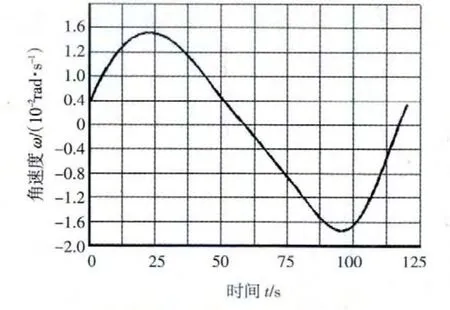
圖5 搖桿角速度-時間圖
1.2 驗證A點的正確性
由于∠C2C1O1=90°-θ,即∠C1O1O2=θ,所以∠C1O1C2=2θ,因此∠C1AC2=θ(同弧所對的的圓周角是圓心角的一半),所以A點在圓Ⅰ上是正確的。
連接O2A,由于∠C1O1O2=∠C2O1O2=θ,所以∠C1AO2=∠C2AO2=θ/2,又因為O2C1=O2E(同圓的兩條半徑相等),O2A為公共邊,則ΔO2C1A≌ΔO2EA,所以AC1=AE,而2l1=C2E=AC2-AE=AC2-AC1,即 lAC2-lAC1=2lAB,所以 A 點的位置正確。
1.3 確定各桿的長度
若給出的曲柄AB的長度l1=120 mm,搖桿CD的長度l3=420 mm,搖桿擺角φ=33.31°,搖桿的行程速比系數K=1.06,曲柄為原動件,轉速n=0.5 r/min,利用上述方法可以求得機架AD的長度l4=500 mm和連桿BC的長度l2=350 mm。下面就利用ANSYS對搖桿CD的角位移、角速度、角加速度隨時間變化的情況進行分析。
2 利用ANSYS對平面搖桿機構做瞬態分析[4]
由于在ANSYS中標準單位是m,所有數據都需換算成以m為單位的數值。
以A點為原點,AD所在直線為x軸,建立直角坐標系,初始位置設 φ1=60°,即 A(0,0)、B(0.06,0.103 92)、C(0.292 76,0.365 31)、D(0.5,0)。
1)分析步驟:設置工作名→設置變量→創建單元類型→定義材料特性→定義實常數→創建節點→指定單元屬性(鉸鏈單元)→創建鉸鏈單元→指定單元屬性(梁單元)→創建梁單元→打開大變形選項→確定第一個載荷步時間和時間步長→設定非線性分析的收斂值→施加約束→求解→定義變量→對變量進行數學操作→查看結果。
2)列表顯示角位移、角速度。搖桿角位移最大值為0.581 401 rad,換算為角度制為33.311 8°;計算出t=0 s時,φ1=60°,當 φ1=120°時,t=20 s;從列表中查得,t=20 s時,ω3=1.497 82×10-2rad/s,對比有機械原理法計算得出的ω3=1.490 36×10-2rad/s,可以看出有限元解是正確的,且有相當高的精度。
角位移、角速度、角加速度隨時間變化圖如圖4~圖6所示。
3 結語
本文首先利用輔助線法求解了特定桿長的曲柄搖桿機構,然后利用ANSYS對該機構進行了分析,得到的結果與圖解法計算出來的結果誤差小,精度高,方法較簡單,只要替換參數就可以得到任何四桿機構的運動瞬態分析結果。
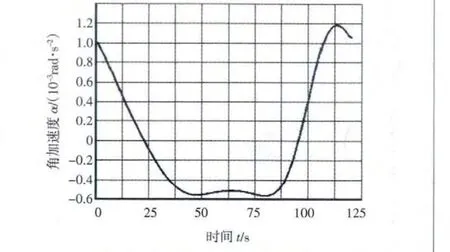
圖6 搖桿角加速度-時間圖
[1] 冀曉紅.具有急回運動特性的曲柄搖桿機構設計[J].機械研究與應用,2008,21(3):75-76.
[2] 孫恒.機械原理[M].北京:高等教育出版社,2008.
[3] 李杰,郭瑞杰,王忠.實現特定桿長的曲柄搖桿機構設計[J].機械設計,2012,29(7):43-45.
[4] 高耀東.ANSYS機械工程應用精華30例[M].北京:電子工業出版社,2010.

