循環競爭博弈的線性控制
唐長慶,田寶國,王 棟(海軍航空工程學院.研究生管理大隊;.基礎部,山東煙臺264001)
?
循環競爭博弈的線性控制
唐長慶a,田寶國b,王棟b
(海軍航空工程學院a.研究生管理大隊;b.基礎部,山東煙臺264001)
摘要:研究了最近鄰空間循環競爭博弈對應的反應擴散方程及其控制動力學,通過相應的數值模擬,得到常參量控制和單變量線性控制的結果,針對各種螺旋波漂移現象,由數值計算得到螺旋波波頭的漂移軌跡,以及平均漂移速率的時間曲線,并進一步擬合得出整個漂移過程的平均速率隨控制參量變化的函數。
關鍵詞:循環競爭博弈;斑圖;線性控制;螺旋波漂移
循環競爭是自然界和人類社會普遍存在的一種現象。有關循環競爭博弈及其擴散的理論與模擬研究結果表明,物種個體的空間分布與擴散均出現復雜的斑圖涌現現象[1-4],例如,在某些條件下出現不規則斑塊,而在其他條件下出現靶波、行波以及各種螺旋波及其擴散運動現象[5-8]。螺旋波在各種可激發系統和種群動力學中相當普遍,如Belousov-Zhabotinsk反應[9-10]、心臟組織[11]、種群動力學[12]和移動的循環競爭種群[1]。螺旋波在種群動力學中很重要,特別是在隨機相互作用的循環競爭種群中,生物多樣性可以通過相互纏繞的螺旋波來得到維持和保持穩定[1,3]。
考慮到現實情況的復雜性,例如,由于地理條件的影響,使得物種捕食、繁殖等活動強度沿地理分布逐漸衰減或增強,這些因素的影響可以通過對反應擴散方程添加控制項來進行研究。本文就是通過在反應擴散方程基礎上加入控制項,來研究上述因素對循環競爭博弈及其擴散運動的影響,研究的情況包括常參量控制和單變量線性控制。
1 反應擴散方程與控制動力學

根據T. Reichenbach等的工作[1,3],只考慮最近鄰相互作用模式下的循環競爭博弈,研究其熱力學極限情況。反應擴散方程組如下:式(1)中:ρA(,,t )、ρB(,,t )、ρC(,,t )分別為物種A、B、C所占的比例;μ為消滅率;σ為繁殖率;d為正常擴散系數。給式(1)加上控制項f,控制項加在方程右端除擴散項外的所有其他項上,得:

在以下的反應擴散方程數值模擬過程中,均采用256×256網格,邊長為1,最小時間間隔Δt=0.1,使用無流邊界條件,采用的數值模擬方法為隱式歐拉法。
2 線性控制與螺旋波漂移

控制項表示為式中:L=256;b1、b2是可調參量。當b2=0時,即為常參量控制。
在數值模擬過程中,選擇合適參量值,會出現3物種空間分布與擴散對應的單臂螺旋波。通過仿真模擬發現,當b2=0且0

圖1 螺旋波波頭的軌跡曲線與3物種的分布斑圖Fig.1 Trajectorcurve of spiral wave tip and the distribution spot pattern of the three species
當b2≠0時,選擇單臂螺旋波穩定漂移為判據,可以得到控制參量b1與b2的關系曲線,如圖2所示。

圖2 控制參量b1、b2的關系曲線Fig.2 Relation curve of control parameter b1and b2
圖2中虛線所示曲線是對b1與b2的關系擬合出來的,擬合所得函數如下:

由式(4)可知,虛線所示曲線是一拋物線。
圖2中陰影部分(包括曲線)為單臂螺旋波穩定漂移的參量區域,其范圍為0.4≤b1≤4.6、0 圖3 a)~c)從左至右分別對應b1=1.0、b1=3.2、b1=3.9時3物種的自組織斑圖。在單臂螺旋波不穩定區,會有2個物種逐漸消失,最終只留下1個物種;或者,先是由單臂螺旋波分裂為多臂螺旋波,經過長時間演化,最終只有1個物種存留下來,哪1個物種能夠存活是隨機的。圖3 d)為b1=2.0且b2=3.0時對應的自組織斑圖。 從螺旋波的漂移過程可以得知,b1是全局性控制項,它影響的是種群在整個空間的繁殖率和消滅率,其越大螺旋波的波長越小;b2是空間梯度控制項,主要影響的是物種在各個位置處的繁殖率和消滅率,其越大螺旋波波頭漂移的速率越大。 圖3 不同控制參量下形成的自組織斑圖Fig.3 Self-organizing spot pattern formed under different control parameters 為了清楚地描述螺旋波的漂移軌跡,我們取一特殊情況進行研究,取b1=2.0,使b2由0遞增,即f沿軸正方向線性增加,新的繁殖率與消滅率同樣隨坐標線性增加。模擬代數最大為105,進行數值模擬,得到各種情況下螺旋波波頭漂移的軌跡曲線與3物種的分布斑圖,分別見圖4 a)~e)。 圖4 螺旋波波頭的軌跡曲線與3物種的分布斑圖Fig.4 Trajectorcurve of spiral wave tip and the distribution spot pattern of the three species 由圖4 a)~e)可知,螺旋波波頭的漂移方向是沿一傾斜直線,即沿坐標、減小(左偏下)的直線方向,但具體軌跡是沿傾斜直線方向的不規則曲線,b2值越大,平均飄移速率越大,針對參量b2的取值,以3 000代為時間間隔計算得到螺旋波波頭漂移的平均速率-v、-v,見圖5 a)。由圖5 a)發現-v、-v圍繞相應的均值呈波動變化,進一步可求出整個漂移期間的平均速率值,得到平均速率與參量b2的關系曲線,見圖5 b)。 圖5 螺旋波波頭漂移的平均速率曲線Fig.5 Average velocitcurve of spiral wave tip drift 對圖5 b)中平均速率-v、-v與參量b的關系曲線 2進行擬合,得到擬合函數關系式:,可見,-v≈2-v。 由以上研究結果可以得知,加入控制項后螺旋波會出現漂移,在控制項f中,參量b1是全局性控制項,其越大螺旋波的波長越小;b2是空間梯度控制項,其越大螺旋波波頭漂移的速率越大。通過大量的數值模擬,得到了單變量線性控制情況下單臂螺旋波穩定漂移的b1與b2關系圖,以及螺旋波波頭的漂移軌跡及其平均速率-v、-v關系曲線。 參考文獻: [1]REICHENBACH T,MOBILIA M,FREE. Mobilitpromotes and jeopardizes biodiversitin rock-paper-scissors games[J]. Nature,2007,448:1046. [2]REICHENBACH T,MOBILIA M,FREE. Noise and correlations in a spatial population model with cclic competition[J]. Phsical Review Letters,2007,99:238105. [3]REICHENBACH T,MOBILIA M,FREE. Self-organization of mobile populations in cclic competition[J]. Journal of Theoretical Biolog,2008,254:368. [4]REICHENBACH T,FREE. Instabilitof spatial patterns and its ambiguous impact on species diversit[J]. Phsical Review Letters,2008,101:058102. [6]BUDRENE E O,BERG H C. Dnamics of formation of smmetrical patterns bchemotactic bacteria[J]. Nature,1995,376:49. [7]BEN JACOB E,SCHOCHET O,TENENBAUM A,et al. Generic modeling of cooperative growth patterns in bacterial colonies[J]. Nature,1994,368:46. [9]ZAIKIN A N,ZHABOTINSKA M. Concentration wave propagation in two-dimensional liquid-phase selfoscillating sstem[J]. Nature,1970,225:535. [10]WINFREE A T. Spiral waves of chemical activit[J]. Science,1972,175:634. [11]DAVIDENKO J M,PERTSOV A V,SALOMONSZ R,et al. Stationarand drifting spiral waves of ecitation in isolated cardiac muscle[J]. Nature,1992,355:349. [12]HASSELL M P,COMINS H N,MAR M. Spatial structure and chaos in insect population dnamics[J]. Nature,1991,353:255. Linear Control Research of Ccle Competition Game TANG Chang-qinga, TIAN Bao-guob, WANG Dongb Abstrraacctt:: In this paper, the corresponding reaction-diffusion equation and control dnamics of the nearest-neighborspace cclical competition game was studied. Through the corresponding numerical simulation, the results of constant pa?rameter control and the linear single-variable control were got. To the varietof spiral wave drifting phenomenon, the tra?jectorof the spiral wave drifting and the average drifting velocitdistribution over time were obtained through the numeri?cal calculation, further the fitted function of average velocitchanging with control parameters in the whole drift process was got. 作者簡介:唐長慶(1989-),男,碩士生。 基金項目:學院基礎研究基金資助項目 收稿日期:2014-11-20; DOI:10.7682/j.issn.1673-1522.2015.02.023 文章編號:1673-1522(2015)02-0197-04 文獻標志碼:A 中圖分類號:O231.1 修回日期:2015-01-14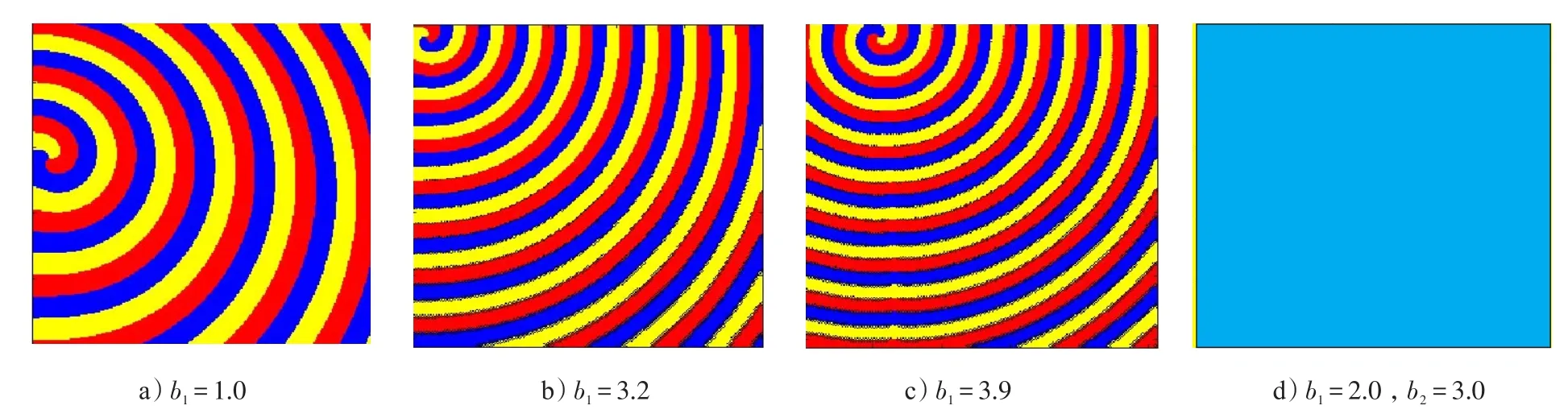




3 結論
(Naval Aeronautical and Astronautical Universita. Graduate Students’Brigade; b. Department of Basic Sciences,antai Shandong 264001, China)

