基于混沌神經網絡的防空火箭炮交流伺服系統狀態預測研究

胡健，馬大為，姚建勇，劉龍

（南京理工大學機械工程學院，江蘇南京210094）

基于混沌神經網絡的防空火箭炮交流伺服系統狀態預測研究

胡健，馬大為，姚建勇，劉龍

（南京理工大學機械工程學院，江蘇南京210094）

為了更加準確地對系統非線性非平穩狀態趨勢進行預測，運用基于神經網絡的混沌預測方法對防空火箭炮交流伺服系統的速度量進行了預測，為基于速度預測值的系統非線性非平穩狀態趨勢預測奠定了基礎。利用C-C法選擇了合適的嵌入維和時間延遲，對防空火箭炮交流伺服系統不規則運動的實驗數據進行了相空間重構并進行了分析。在原Elman網絡中增加了輸出層關聯單元，并把自反饋增益系數當作連接權值投入到網絡的訓練中，以增強Elman網絡非線性逼近能力，在此基礎上建立了基于改進型Elman網絡的混沌預測模型。采用基于最大Lyapunov指數預測法和混沌神經網絡預測法對系統狀態進行了預測，兩種方法的預測結果表明，后一種方法對防空火箭炮交流伺服系統速度值預測精度更高，從而使得基于此的系統非線性非平穩狀態趨勢預測更有效。

兵器科學與技術；火箭炮；交流伺服系統；狀態預測；相空間重構；混沌神經網絡

0　引言

防空火箭炮交流伺服系統由永磁同步電機、驅動器、減速器及相應的負載組成，是一種典型的電機傳動系統，同時也是一種典型多變量強耦合的非線性系統。其不規則運動的存在由來已久，主要表現為轉矩、轉速的間歇振蕩、控制性能的不穩定、系統不規則電磁噪聲等［1］，它們的出現直接影響系統的總體性能和可靠性。長期以來，由于交流傳動系統的復雜性，人們往往把這些不規則運動的產生歸結為外界隨機干擾或系統故障，并用傳統的平穩信號分析方法去分析，以期解決問題。這種認識上的局限性束縛了人們解決問題的思路。目前已有部分研究表明，在某些參數工作條件下，類似防空火箭炮交流伺服系統的機電傳動系統會出現混沌運動［1-3］，其動力學特性往往表現出復雜性和非線性。此時，傳統的平穩信號分析方法不再適用，若對這些非線性問題進行線性化處理，系統的輸出將遠離事實本相。因此，運用非線性動力學從混沌的角度分析防空火箭炮交流伺服系統的不規則運動并進行狀態預測與故障診斷有十分重要的意義。

非線性系統的混沌預測方法分為兩大類：一是基于非線性數學模型的動力學方法，二是基于實際觀測數據的相空間重構法。前者根據實際問題建立描述系統的動態數學模型，然后求解這個數學模型，最后反過來根據計算結果進行預測。但由于非線性系統本身的復雜性，在建立數學模型的過程中，需要事先做出一定的假設和近似處理，這就使得建立的數學模型并不那么精確，從而使得基于該模型的混沌預測效果不是很理想。而用相空間重構法進行預測時，在預測之前不用做任何假設與數據處理，而是直接利用采集的非線性系統時間序列進行分析，得到時間序列幾何不變量進行預測，這樣減少了預測的主觀性，預測效果也更好。

常見的基于相空間重構的混沌時間序列預測方法有全局預測法［4］、局域預測法［5］以及基于最大Lyapunov指數的預測方法［6-7］。最近幾年，神經網絡因為其強大的非線性系統逼近擬合能力而被引入到非線性系統的混沌預測中來［8-10］，神經網絡被用來構造一個非線性映射來近似地還原原系統，這一非線性映射即為要建立的預測模型。但這些混沌預測算法仍然存在不少的缺陷，如收斂速度慢，預測精度不高等。本文利用改進的Elman網絡逼近嵌入空間中的相點演化規律，利用觀測得到的時間序列歷史數據建立時間序列的預測模型。結果表明，該方法對防空火箭炮交流伺服系統具有較好的非線性擬合能力和較高的預測精度。

1　防空火箭炮交流伺服系統實驗現象

1.1防空火箭炮交流伺服系統的組成

防空多管火箭炮交流伺服系統由俯仰和方位兩個軸上的交流伺服系統組成。每一個軸上的交流伺服系統主要由位置控制器、伺服驅動器、永磁同步電機、減速器、機械機構、旋轉變壓器以及電源組成。具有接受指揮系統的目標指示、進行俯仰和方位自動調炮以及目標跟蹤的功能。具體的工作原理如下：炮位計算機通過串口將目標未來點位置發送給位置控制器，位置控制器通過其上的軸角轉換電路采集旋轉變壓器送來的當前位置，經過控制律計算出控制量，通過D/A轉換控制驅動器帶動相應的伺服電機運轉，再經過減速器帶動相應的機械機構運動，從而實現高精度調炮和跟蹤。其組成框圖如圖1所示，原理樣機如圖2所示。

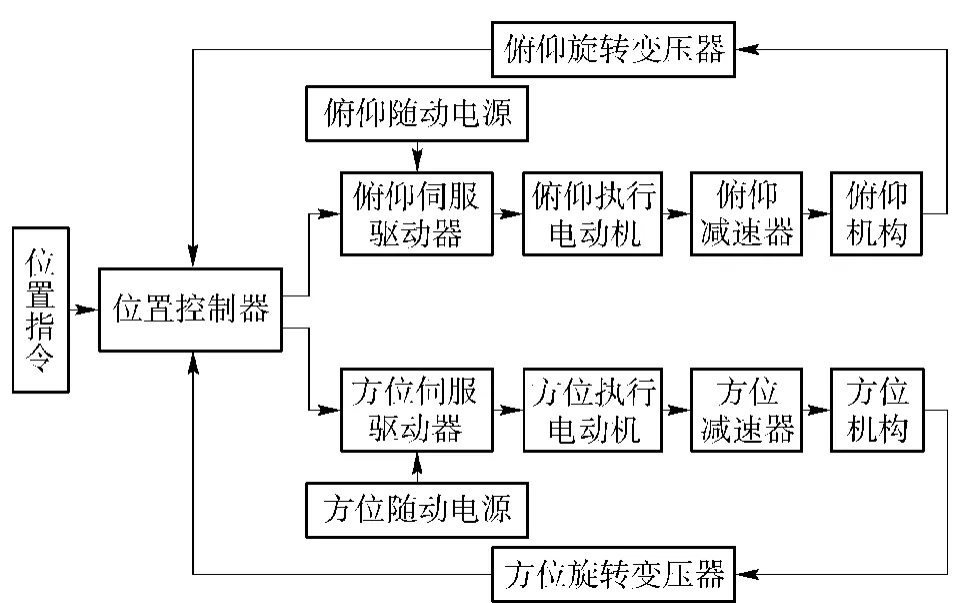
圖1　防空火箭炮交流伺服系統組成框圖Fig.1 Block diagram of air-defense rocket launcher

1.2實驗現象

由于方位軸和俯仰軸交流伺服系統的組成、結構是完全一樣的，因此我們以其中一軸（俯仰軸）為例進行分析。通過改變驅動器的控制參數來改變閉環系統的動態特性。大量實驗發現，隨著控制參數的改變，防空火箭炮交流伺服系統先后出現3種典型運動狀態：1）轉速平穩無波動，如圖3（a）所示；2）轉速呈周期性波動，周期性波動呈近似正弦波形，具有固定周期，如圖3（b）所示；3）轉速含有不規則波動，其沒有明顯的波動周期，是一種較為復雜的不穩定性現象，如圖3（c）所示。目前還沒有相關研究成果能夠精確預測第3種不規則運動，本文利用基于改進Elman網絡的混沌時間序列預測方法預測這種不規則運動。

圖2　防空火箭炮交流伺服系統原理樣機Fig.2 Prototype of air-defense rocket launcher

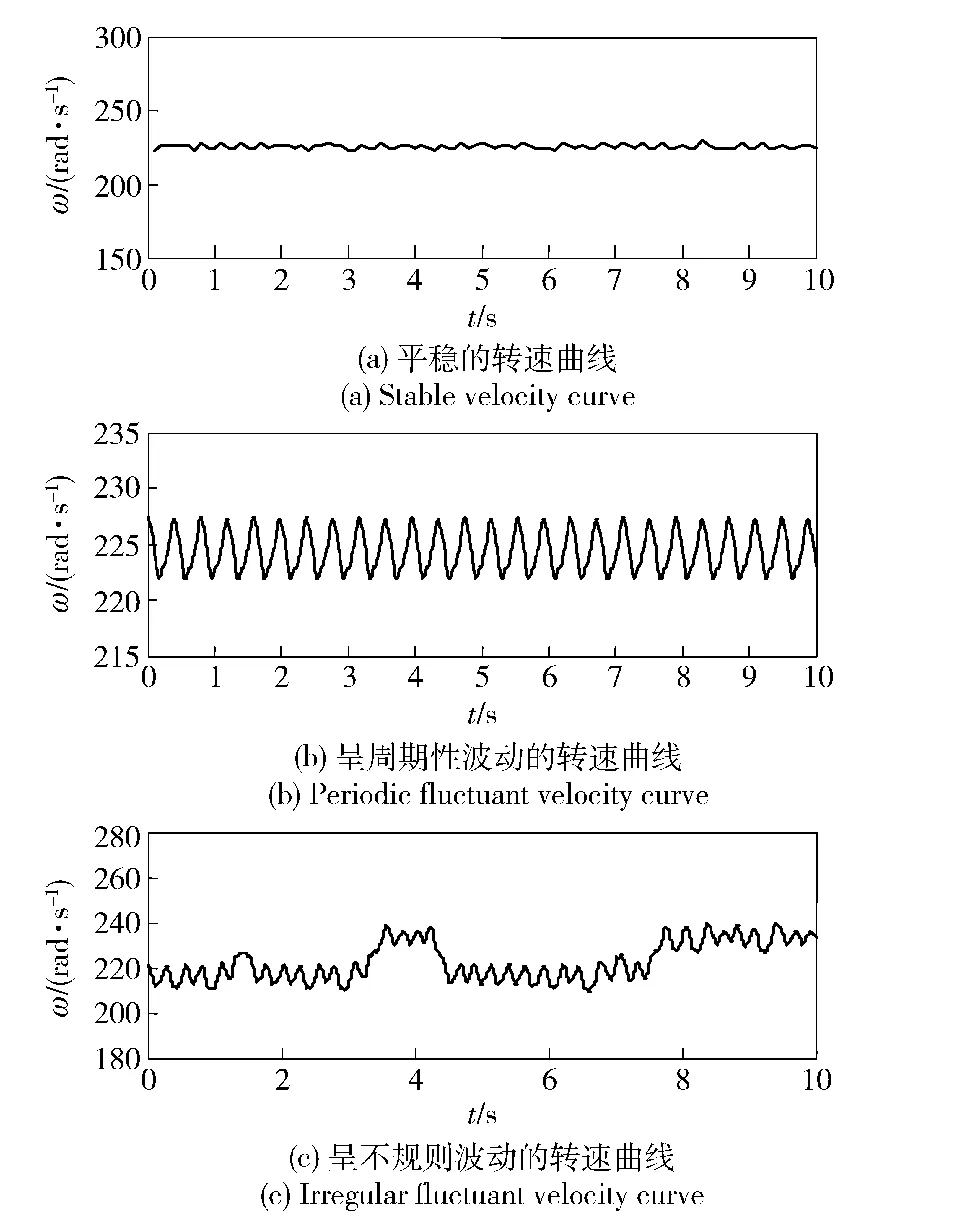
圖3　防空火箭炮交流伺服系統不同參數下轉速曲線Fig.3 Velocity curves under different parameters

2　防空火箭炮交流伺服系統混沌預測算法

2.1相空間重構

為了有效恢復高維復雜動力學系統的混沌動力學特性，相空間重構理論被提出。其基本思想是：系統中任一分量的演化都是由與之相互作用的其他分量所決定的，因此這些相關分量的信息就隱藏在任一分量的發展過程中。為了重構一個等價的狀態空間，只需考察一個分量，并將它在某些固定的時間延遲點上的測量作為新維處理，即延遲值被看成是新的坐標，它們確定了某個多維狀態空間中的一點。重復這一過程并測量相對于不同時間的各延遲量就可以產生出許多這樣的點，該方法可以將吸引子的許多性質保存下來，即用系統的一個觀察量可以重構出原動力系統模型，初步確定系統真實相空間的維數［11］。

設時間序列為x（t），t=1，2，…，N，嵌入維數為m，時間延遲為τ，則重構相空間為

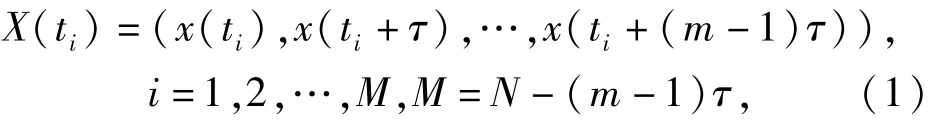
式中：X（ti）為m維相空間中的相點；M為相點個數；集合｛X（ti）|i=1，2，…，M｝描述了系統在相空間中的演化軌跡。根據Takens定理，只要m、τ選擇合理，重構相空間與原系統是拓撲等價的。因此存在一個光滑映射f∶Rm→Rm給出相空間軌跡的表達式為

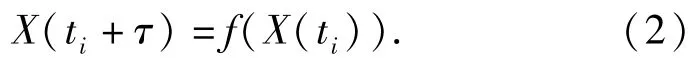
上述映射可表示成時間序列為

根據此方法，我們只需采集防空火箭炮交流伺服系統的一個狀態變量（如電流、速度或位置），通過相空間重構即可恢復原系統非線性動力學特性，從而進行狀態預測。在眾多狀態變量中，角速度可以更加直觀地反映系統運動特性且較易測得，因此本文在防空火箭炮交流伺服系統所獲得的最優控制算法的控制下，采集系統角速度輸出構成一維時間序列，采樣時間間隔為20 ms，共采集3 000個點，利用此一維時間序列進行相空間重構。

2.2嵌入維和時間延遲的選取

在重構相空間中，時間延遲τ和嵌入維數m的選取具有十分重要的意義，同時這種選取也是很困難的。由于實際時間序列存在噪聲干擾，如果τ太小，相空間軌跡會向同一位置擠壓，信息不易顯露，產生冗余誤差；如果τ太大，會導致某一時刻和后一時刻的動力學特性變化劇烈，使得簡單的幾何對象變得很復雜，動力系統信號失真，產生不相關誤差。

目前常用的τ估計方法有自相關函數法和互信息法，前者適用于小數據組，計算方便，但不適合非線性問題，后者適用于大數據組，適合非線性問題，但計算不方便。Kim等提出一種改進方法，稱為C-C方法，該方法應用關聯積分能夠同時估計出m和τ，容易操作，計算量小，效果好，而且具有較強的抗噪聲能力（30%以下）［10］。本文采用C-C法選取時間延遲τ和嵌入維數m，具體步驟如下：

在此基礎上，對3組實驗數據進行相空間重構，來觀察一下實驗數據有何特點。

圖5為轉速相空間重構的相軌跡，轉速相空間重構的相軌跡與系統相空間的相軌跡在表現系統的動力學本質特性上是等價的。圖5（a）表明系統在做周期2運動，圖5（b）表明系統在做擬周期運動，圖5（c）表明系統進入混沌狀態，在做混沌運動。從中可以看出隨著系統參數的變化，系統從平穩運動狀態進入周期運動狀態，直至進入混沌運動狀態。

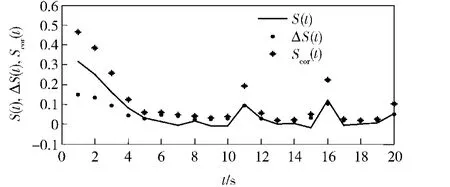
圖4　隨t的變化曲線Fig.4 Curves of

2.3基于混沌神經網絡的狀態預測

選擇好合適的嵌入維和時間延遲，重構好相空間，就可以用混沌預測的方法預測系統狀態。混沌預測方法就是在相空間中找到一個非線性模型，去逼近系統動態特性，即前面所說的光滑映射f∶Rm→Rm，實現一定時間內的預測，同時該模型也可用來識別系統是否包含混沌特性［10］。神經網絡是非線性系統逼近和建模的有效工具，在混沌時間序列的重構相空間中，可以利用神經網絡逼近相點的演化規律，利用觀測得到的時間序列歷史數據建立時間序列的預測模型。基于混沌神經網絡的預測原理圖如圖6所示。

采用神經網絡進行序列建模和預測時，首先要考慮網絡結構的設計問題。神經網絡的拓撲結構不僅影響到網絡的泛化能力，同時也影響網絡的學習速度。文獻［8-9］分別探討了徑向基函數（RBF）神經網絡、反向傳播（BP）神經網絡的混沌時間序列預測問題。這些算法比較復雜，運行的時間較長，且預測精度不高，收斂速度慢。從（1）式可以看出系統某一瞬時狀態可由m維的延遲坐標向量確定，因此在網絡結構中應該包含延時單元，以反映延遲坐標向量對系統狀態的影響。而RBF神經網絡、BP神經網絡均不包含這樣的單元，因此不能較好地反映系統的動態特性。最近提出的一種Elman神經網絡［11］在前饋網絡的隱含層中增加一個承接層，作為一步延時算子，達到記憶的目的，從而具有適應時變特性的能力，能直接反映動態系統的特性。因此，本文利用Elman網絡進行系統混沌預測。

為了增加神經元對歷史數據的敏感程度，本文在原Elman網絡中增加了輸出層關聯單元，以存儲輸出層的歷史數據，并反饋給輸出單元。此外，標準Elman網絡中自反饋增益α是固定值，一般是根據經驗來選取，α值選擇得不好會導致系統出現發散現象。本文考慮把各個α當作連接權值投入到網絡的訓練中，從而實現自反饋增益系數的動態修正。由此設計了一個適于本系統混沌預測的改進型Elman網絡，其結構如圖7所示。Elman神經網絡采用經典的梯度下降法進行在線訓練學習，權值初值可選一個隨機值，經過梯度下降法訓練后會收斂到一個穩態值［12］。改進后的Elman網絡具有較高的收斂精度和較短的學習時間。由于系統速度量經過相空間重構后的相點運動軌跡可以反映出系統的動力學特性，所以混沌神經網絡的輸入量選為系統相空間中的相點ω（ti），ω（ti+τ），ω（ti+2τ），因此輸入層有3個節點。由于進行的是單步預測，輸出量為下一時刻的速度量ω（ti+3τ），所以輸出層和輸出層關聯單元只有1個節點，隱層和隱層關聯單元節點數的選擇至關重要，多了則增加計算量影響預測速度，少了則影響存儲記憶能力導致預測精度降低，綜合考慮這兩個因素根據經驗選為4個節點，則網絡的狀態空間表達式如圖7所示。

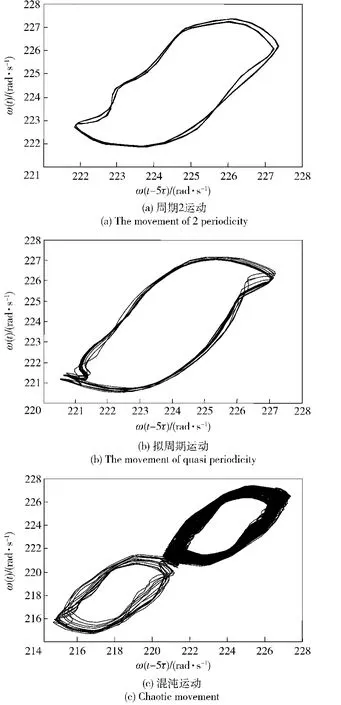
圖5　防空火箭炮系統相空間重構的相軌跡Fig.5 Phase orbit of air defense rocket launcher

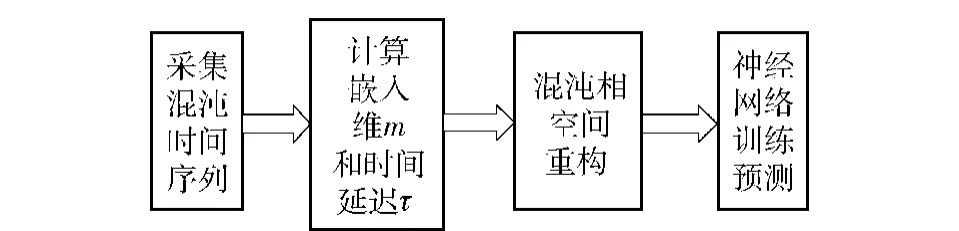
圖6　混沌神經網絡預測原理圖Fig.6 Schematic diagram of chaotic neural network

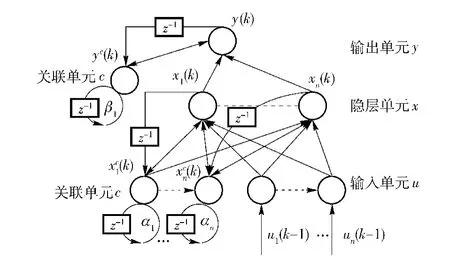
圖7　改進型Elman網絡Fig.7 Improved Elman network

圖7中：u1（k-1），…，un（k-1）為輸入量；

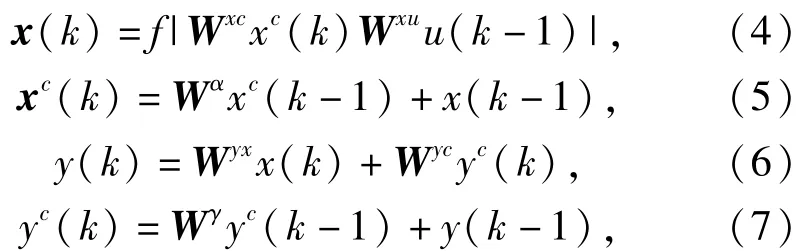
（4）式～（7）式中：Wxc、Wxu、Wyx、Wyc分別為隱層關聯單元到隱層，輸入單元到隱層，隱層到輸出單元及輸出層關聯單元到輸出單元的權矩陣；Wα=diag［α1，…，αn］，Wγ=diag［γ1，…，γn］，為自反饋增益矩陣；閾值函數f選為Sigmoid函數，即f=1/（1+ e-x）；x（k）=［x1（k），x2（k），…，xn（k）］；xc（k）=［xc1（k），xc2（k），…，xcn（k）］.

設第k步系統的實際輸出為yr（k），定義誤差函數為，將E對連接權值及矩陣γ1、Wyx、Wyc、Wα、Wxu、Wxc分別求偏導，由梯度下降法可得Elman網絡的學習算法為

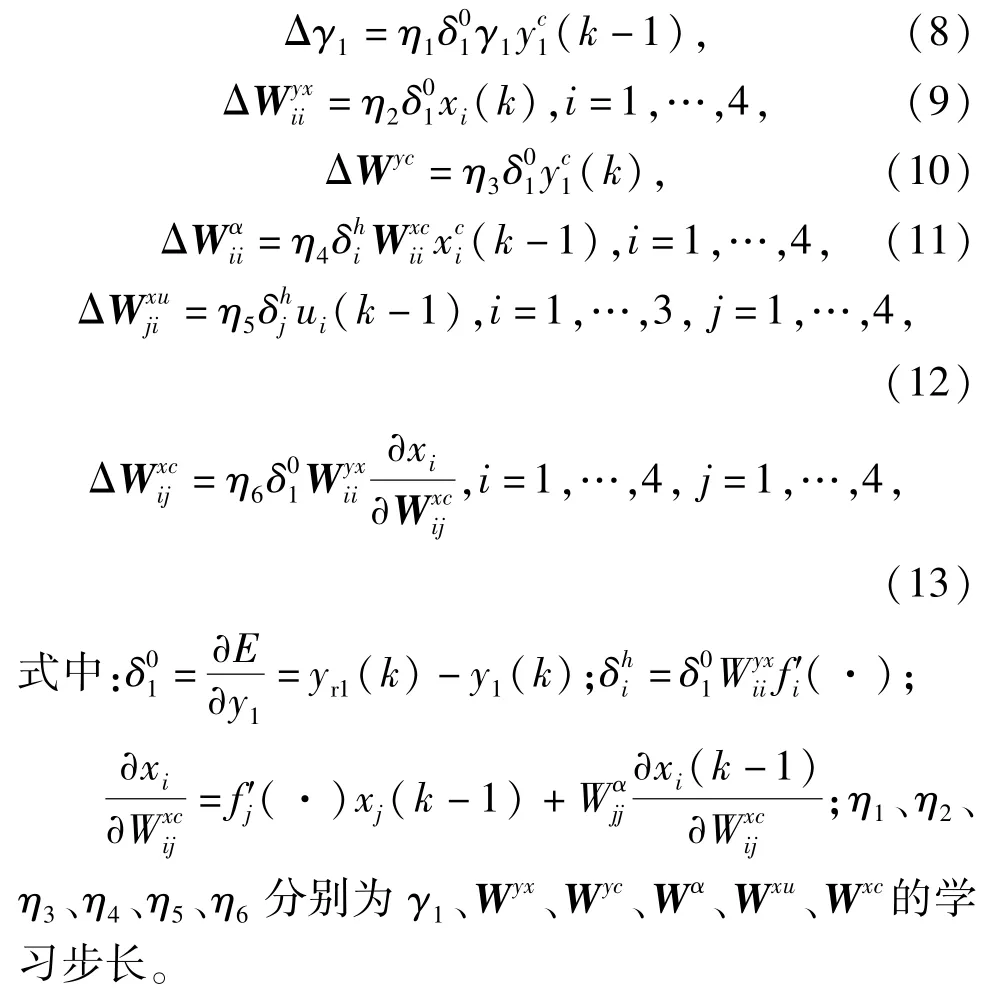
3　預測分析

混沌預測神經網絡結構和訓練算法建立之后，就可以開始對混沌神經網絡進行訓練，即進入學習階段。采集防空火箭炮交流伺服系統的速度數據，輸入網絡輸入層，得到輸出結果，然后與實際數據進行比較，如果存在誤差，立即進行反向傳播過程，并修正網絡權值以減小誤差。正向輸出計算和反向權值修改交替進行。

經過反復的訓練，網絡的權值已經達到了預測的要求，然后將此混沌神經網絡應用到防空火箭炮交流伺服系統狀態預測中，對經過降噪的數據進行后期趨勢預測。為了比較方法的優越性，將基于Elman網絡的混沌神經網絡預測法與基于最大Lyapunov指數的預測方法進行比較，采集的數據是系統處于混沌運動狀態時的速度值，結果如圖8和表1所示。通過與基于最大Lyapunov指數的預測方法進行比較可以看出，混沌神經網絡預測法的預測精度比較高，預測效果更理想。同時可以看出，由于混沌系統的耗散性和對初值的極端敏感性，在短期內預測精度很高，但長時間預測誤差急劇增大，說明混沌動力系統只能作短期預測。需要說明的是，不同的神經網絡權值初值的選取有可能導致系統陷入局部最小點，從而導致預測精度的降低。為了避免出現這種情況，可以在梯度更新法中增加一個沖量項以帶動梯度下降過程，沖過狹窄的局部最小值而到達全局最小值。

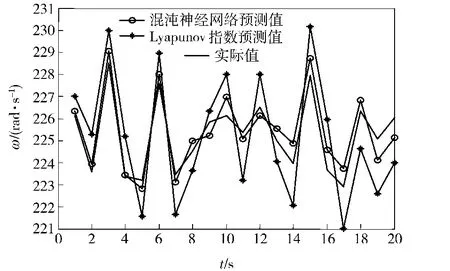
圖8　混沌神經網絡預測法與基于最大Lyapunov指數預測法對比圖Fig.8 Comparison of two methods

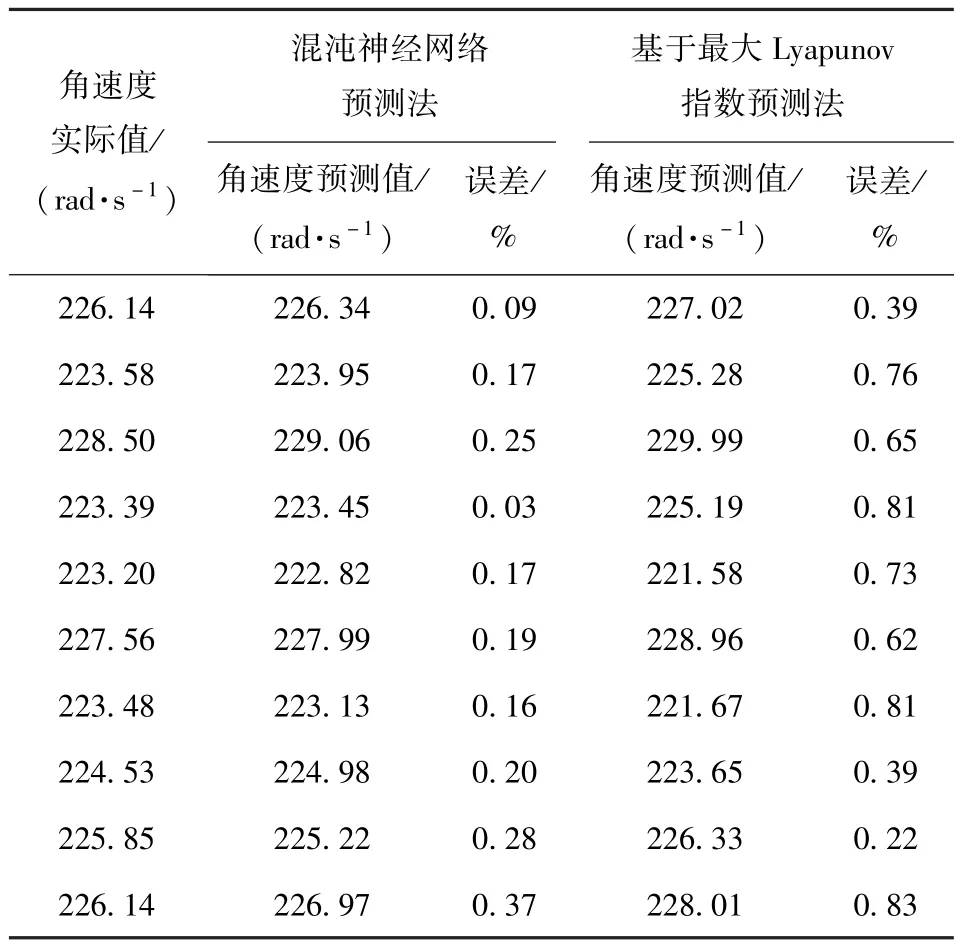
表1　混沌神經網絡預測法與基于最大Lyapunov指數預測法比較Tab.1 Comparison table of two methods

在精確預測系統速度值的基礎上，可以直接觀察已經測得的角速度和預測的角速度序列的時序圖或相空間重構后的相圖判斷系統的當前狀態，如圖3、圖5所示。也可以利用已經測得的角速度和預測的角速度序列根據最小數據量法［13］計算出系統最大Lyapunov指數，從而準確判斷系統是否進入非線性非平穩狀態（即混沌狀態）。

4　結論

基于混沌神經網絡的預測是通過基于數據序列客觀存在的內在混沌特性實現的，神經網絡的預測模型輸入端完全由混沌特征決定，這樣避免了以往預測方法中主觀確定因素的影響。通過與基于最大Lyapunov指數的預測法進行比較可以看出，混沌神經網絡預測法的預測精度比較高，預測效果較理想。在此基礎上，可以更加準確地對系統非線性非平穩狀態進行趨勢預測。

（

）

［1］張波，李忠，毛宗源，等.電機傳動系統的不規則運動和混沌現象初探［J］.中國電機工程學報，2001，21（7）：40-45. ZHANG Bo，LI Zhong，MAO Zong-yuan，et al.A primary study on an erratic behavior and chaotic phenomena of electric machine drive systems［J］.Proceedings of the CSEE，2001，21（7）：40-45.（in Chinese）

［2］Li Z，Paris J B，Joo Y H，et al.Bifurcations and chaos in a permanent-magnet synchronous motor［J］.IEEE Transactions on Circuits and Systems-I：Fundamental Theory and Applications，2002，49（3）：383-387.

［3］Jing Z，Yu C，Chen G.Complex dynamics in a permanent-magnet synchronous motor model［J］.Chaos，Solitons and Fractals，2004，22（4）：831-848.

［4］張森，肖先賜.混沌時間序列全局預測新方法-連分式法［J］.物理學報，2005，54（11）：5062-5068. ZHANG Sen，XIAO Xian-ci.A new method of global prediction for chaotic time series based on continued fractions［J］.Acta Physica Sinica，2005，54（11）：5062-5068.（in Chinese）

［5］郭創新，王揚，沈勇，等.風電場短期風速的多變量局域預測法［J］.中國電機工程學報，2012，32（1）：24-31. GUO Chuang-xin，WANG Yang，SHEN Yong，et al.Multivariate local prediction method for short-term wind speed of wind farm［J］. Proceedings of the CSEE，2012，32（1）：24-31.（in Chinese）

［6］張勇，關偉.基于最大Lyapunov指數的多變量混沌時間序列預測［J］.物理學報，2009，58（2）：756-762. ZHANG Yong，GUAN Wei.Predication of multivariable chaotic time series based on maximal Lyapunov exponent［J］.Acta Physica Sinica，2009，58（2）：756-762.（in Chinese）

［7］張文超，譚思超，高璞珍.基于Lyapunov指數的搖擺條件下自然循環流動不穩定性混沌預測［J］.物理學報，2013，62（6）：060502. ZHANG Wen-chao，TAN Si-chao，GAO Pu-zhen.Chaotic forecasting of natural circulation flow instabilities under rolling motion based on Lyapunov exponents［J］.Acta Physica Sinica，2013，62（6）：060502.（in Chinese）

［8］馮興杰，潘文欣，盧楠.基于小波包的RBF神經網絡網絡流量混沌預測［J］.計算機工程與設計，2012，33（5）：1681-1686. FENG Xing-jie，PAN Wen-xin，LU Nan.Research on chaotic prediction method of network traffic based on wavelet packet［J］. Computer Engineering and Design，2012，33（5）：1681-1686.（in Chinese）

［9］朱春梅，徐小力，張建民.基于混沌神經網絡理論的機電設備狀態趨勢預測研究［J］.北京理工大學學報，2009，29（6）：506-509. ZHU Chun-mei，XU Xiao-li，ZHANG Jian-min.Electromechanical equipment fault forecasting research based on chaos-neural networks theory［J］.Transactions of Beijing Institute of Technology，2009，29（6）：506-509.（in Chinese）

［10］呂金虎，陸君安，陳士華.混沌時間序列分析及其應用［M］.武漢：武漢大學出版社，2001. LYU Jin-hu，LU Jun-an，CHEN Shi-hua.Chaotic time sequence analysis and its application［M］.Wuhan：Publishing House of Wuhan University，2001.（in Chinese）

［11］HE Hai-tao，TIAN Xia.An improved Elman network and its application in flatness prediction modeling［C］∥Second International Conference on Innovative Computing，Information and Control.Piscataway，NJ，US：IEEE Computer Society，2008：44-48.

［12］WU Wei，FENG Guo-rui，LI Zheng-xue，et al.Deterministic convergence of an online gradient method for BP neural networks［J］. IEEE Transactions on Neural Networks，2005，16（3）：533-540.

［13］張海龍，閔富紅，王恩榮.關于Lyapunov指數計算方法的比較［J］.南京師范大學學報，2012，12（1）：5-9. ZHANG Hai-long，MIN Fu-hong，WANG En-rong.The comparison for Lyapunov exponents calculation methods［J］.Journal of Nanjing Normal University，2012，12（1）：5-9.（in Chinese）

State Forecasting Research of Air-defense Rocket Launcher AC Servo System Based on Chaotic Neural Network

HU Jian，MA Da-wei，YAO Jian-yong，LIU Long
（School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China）

To predict the system nonlinear and non-stationary conditions more accurately，a method of chaos prediction based on chaotic neural networks is introduced to predict the velocity of the air-defense rocket launcher AC servo system，which paves the way for the trend prediction of system nonlinear and non-stationary conditions.C-C method is used to select the proper embedding dimension and time delay. The phase space of system is reconstituted using experimental data of system's irregular movement and is analyzed.The context neurons of output layer are added to the original Elman network，and the self-feedback gain coefficients are trained as connective weight，which could strengthen the nonlinear approximation ability of Elman network.Then a model of chaotic neural network based on the improved Elman network is set up.The predictions based on the maximun Lyapunov exponent and chaotic neural network are performed，respectively.The predicted results show that the prediction based on the chaotic neural network has a higher accuracy，which makes the trend forecasting of the system more effectively.

ordnance science and technology；rocket launcher；servo system；state forecasting；phasespace reconstruction；chaotic neural network

TJ713

A

1000-1093（2015）02-0220-07

10.3969/j.issn.1000-1093.2015.02.005

2014-04-23

國家自然科學基金項目（51305203）；“十二五”國防基礎科研項目（B2620110005）；江蘇省博士后基金項目（1302002A）

胡健（1980—），女，講師，碩士生導師。E-mail：hujiannjust@163.com；馬大為（1953—），男，教授，博士生導師。E-mail：ma_dawei@njust.edu.cn