一個新的三維類Lorenz系統(tǒng)的動力學(xué)分析及仿真

張 旻，張宇功，張建強

(蘭州交通大學(xué)數(shù)理學(xué)院，甘肅 蘭州730000)

在非線性系統(tǒng)中，由于系統(tǒng)內(nèi)部相互作用而產(chǎn)生一種非周期行為，我們把這種行為就稱為混沌.混沌是不可測的，這和外在表象與隨機運動類似.但在動力學(xué)中，混沌是確定的，而他的不可測主要來自于運動的不穩(wěn)定性.這種不穩(wěn)定性主要表現(xiàn)為對無論多小的擾動在經(jīng)過一定時間后，會使系統(tǒng)很大的偏離初始狀態(tài).因此，混沌也是非線性系統(tǒng)普遍存在的動力學(xué)行為.

自從1963年美國氣象學(xué)家 Lorenz［1］在研究氣象預(yù)報時提出Lorenz系統(tǒng)以來，混沌理論得到了迅猛的發(fā)展，也成為迄今為止研究最為深入的混沌吸引子.通過對Lorenz系統(tǒng)非線性動力學(xué)的研究，使得許多新的自治混沌系統(tǒng)也相繼提出并得到了很多有趣的結(jié)果.例如:Rossler系統(tǒng)，Chen［2］吸引子，呂氏吸引子［3］等.

本文主要研究了一個類Lorenz系統(tǒng)的混沌系統(tǒng)的動力學(xué)行為.利用非線性動力學(xué)的方法，通過理論推導(dǎo)，以及時序圖、相圖、Lyapunov指數(shù)圖［4-10］、Poincare截面圖、分支圖［11-14］等數(shù)值模擬的方法研究了該系統(tǒng)的動力學(xué)行為.并分析了系統(tǒng)在不同參數(shù)時復(fù)雜的動力學(xué)現(xiàn)象，從數(shù)值和理論上分析了系統(tǒng)的混沌特性.

1 Lorenz系統(tǒng)及其動力學(xué)行為

1.1 類Lorenz系統(tǒng)的模型

著名的 Lorenz系統(tǒng)［1］為

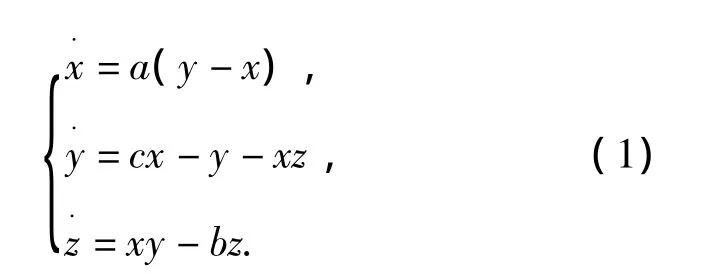
其中(x，y，z)為系統(tǒng)的狀態(tài)變量，a，b，c為系統(tǒng)參數(shù)，且a≠0.系統(tǒng)(1)中含有2個非線性項 xy，xz，當參數(shù) a=10，b=8/3，c=28，該系統(tǒng)呈現(xiàn)混沌狀態(tài).

本文研究的系統(tǒng)如下:

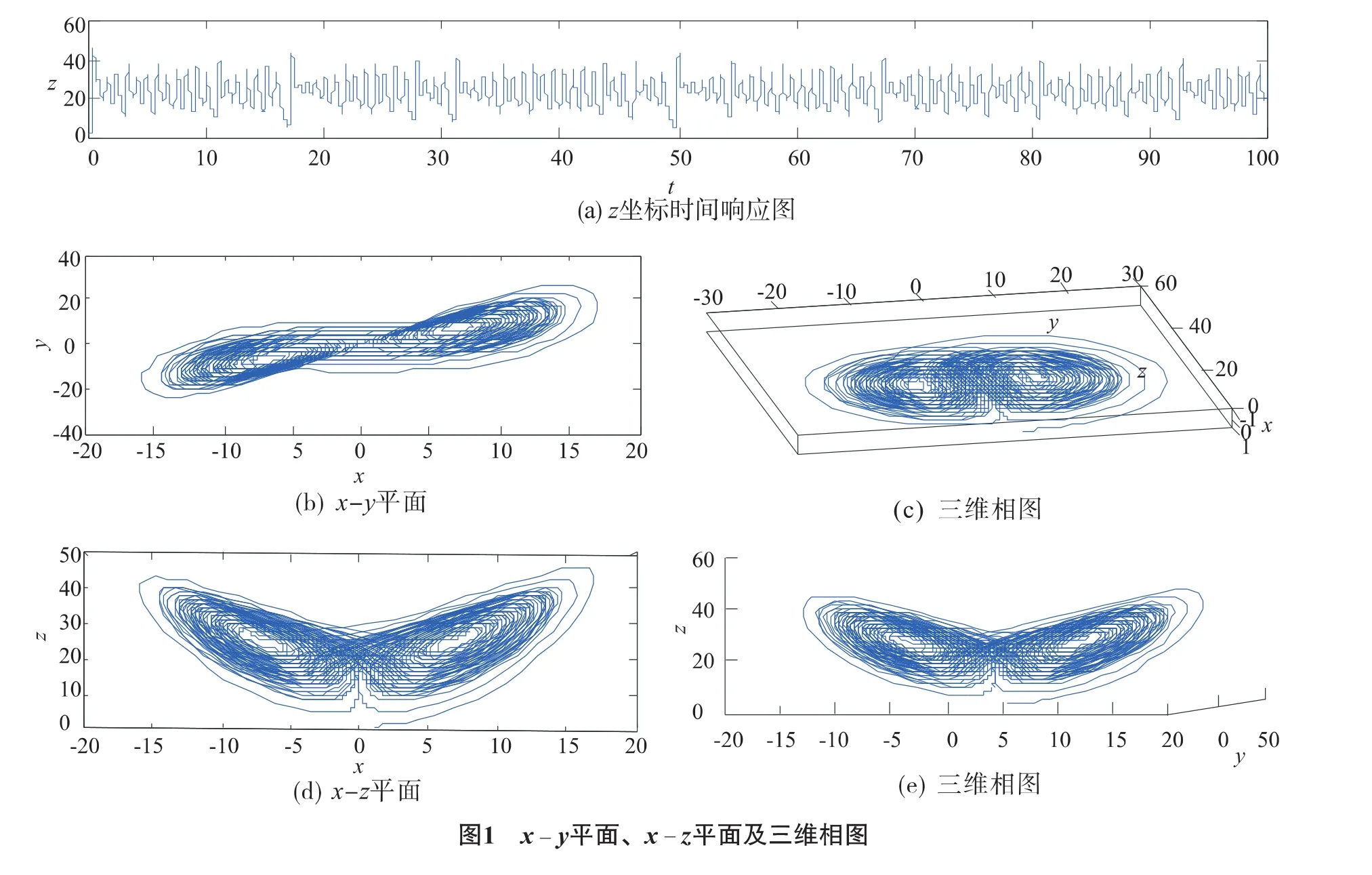
取參數(shù) a=7，b=2，c=25，系統(tǒng)存在一個混沌吸引子，如圖1所示.

1.2 系統(tǒng)平衡點穩(wěn)定性分析

由系統(tǒng)(2)可知，若bc≤0，則系統(tǒng)(2)只有1個平衡點E0(0，0，0);若bc≥0，則系統(tǒng)有3個平衡點E0

定理1 當a＞0，b＞0，c＜0時，平衡點E0是局部漸近穩(wěn)定的.

證明:因為系統(tǒng)(2)在原點處的Jacobian矩陣為

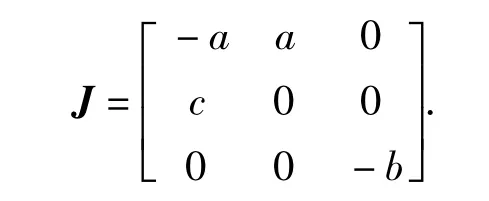
對應(yīng)的系統(tǒng)在原點處的特征方程為

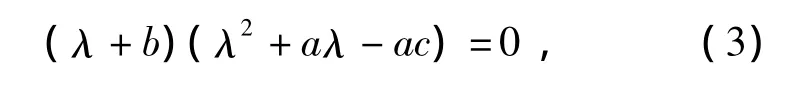
可求得一特征根為λ1=-b，其余2根由方程

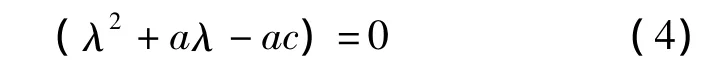
決定.

由Hurwitz判據(jù)，特征方程的全部根都在左半復(fù)平面的充分必要條件是Jacobian行列式的各階主子式均大于0，即

解得a＞0，c＜0.所以，當 a＞0，b＞0，c＜0 時，平衡點E0是局部漸近穩(wěn)定的.

引理1 Hurwitz穩(wěn)定判據(jù)必要條件［15］:系統(tǒng)特征方程的所有根均具有負實部(即系統(tǒng)穩(wěn)定)的必要條件是特征方程中各項系數(shù)為正數(shù).

定理2 當b≠0，ac同號時，平衡點E0不穩(wěn)定.

證明:當b≠0，ac同號，則特征方程(λ +b)(λ2+aλ-ac)=0無零解.若有零解，則有b=0或ac=0，這與條件矛盾.且無純虛根，不然a=0與ac＞0矛盾.其他兩個根由方程(λ2+aλ-ac)=0決定，因為ac＞0，故由引理1得知這兩個根不全具有負實部.而(4)式又無零根或純虛根，所以具有正實部，故平衡點E0不穩(wěn)定.

定理3 當 bc＞0，a＞0，a+b＞c＞0，時，平衡點E1，E2為局部漸近穩(wěn)定.

證明 現(xiàn)證明E2，E1可類似推出.系統(tǒng)(2)在平衡點E2處Jacobian矩陣為

求得系統(tǒng)(2)在平衡點E2處Jacobian矩陣的特征方程為

根據(jù)Hurwitz判據(jù)，式(5)的所有根都在復(fù)平面左半部的充分必要條件是各項系數(shù)所構(gòu)成的主行列式及其順序主子式全部為正，即

可得 a+b＞0，a+b＞c，(a+b)c＞0，又因為當bc≥0 時，存在平衡點 E1，E2.所以，當 bc＞0，a ＞0，以及a+b＞c＞0，平衡點E2漸近穩(wěn)定.

同理可知，當 bc＞0，a＞0，以及 a+b＞c＞0，平衡點E1漸近穩(wěn)定.

綜上所述，當 bc＞0，a＞0，以及 a+b＞c＞0時，平衡點E1，E2為漸近穩(wěn)定.

1.3 平衡點的分支

由平衡點E0處Jacobian矩陣的特征方程(λ+b)(λ2+aλ -ac)=0 可知，不論參數(shù) a，b，c如何變化，特征方程只有零解，而不會出現(xiàn)純虛根，故此平衡點不會發(fā)生Hopf分岔.下面對平衡點E1的Hopf分支進行討論，E2的分支類似.

定理4 當bc＞0，ab＞0，c=a+b時，平衡點E1產(chǎn)生Hopf分支.

證明:當bc≥0時，E1的Jacobian矩陣的特征方程為(5)，有一對共軛純虛根λ1，2= ±iω(ω ＞0)，與另一實根 λ3.易知 λ3=-(a+b)，而 λ1，2滿足特征方程式(5)，代入得 ω=，c=a+b，且 bc＞0，ab＞0.

當c=c0=a+b時，

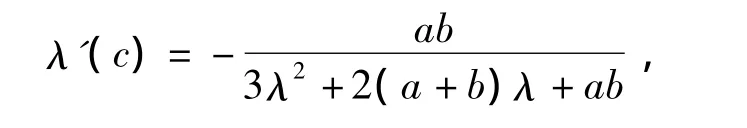
代入c0=a+b得

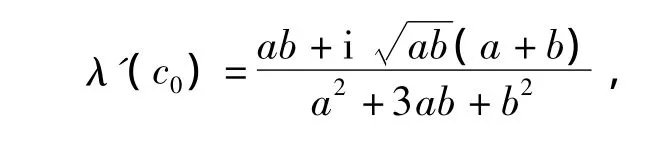
所以，當 bc＞0，ab＞0，c=a+b時，平衡點 E1產(chǎn)生Hopf分岔.

1.4 系統(tǒng)的耗散性

對系統(tǒng)(2)，由于其散度

若 b＞0，a＞0，則 p為負值，此時，系統(tǒng)(2)描述的是一個耗散系統(tǒng)，并以指數(shù)形式=ep收斂.也就是當t→∞時，初始體積為V0的體積元收縮為體積元包含系統(tǒng)軌線的每個小體積元以指數(shù)速率縮減為0，最終系統(tǒng)的軌線會被收縮在一個體積為0的極限子集中，說明系統(tǒng)確實存在吸引子.

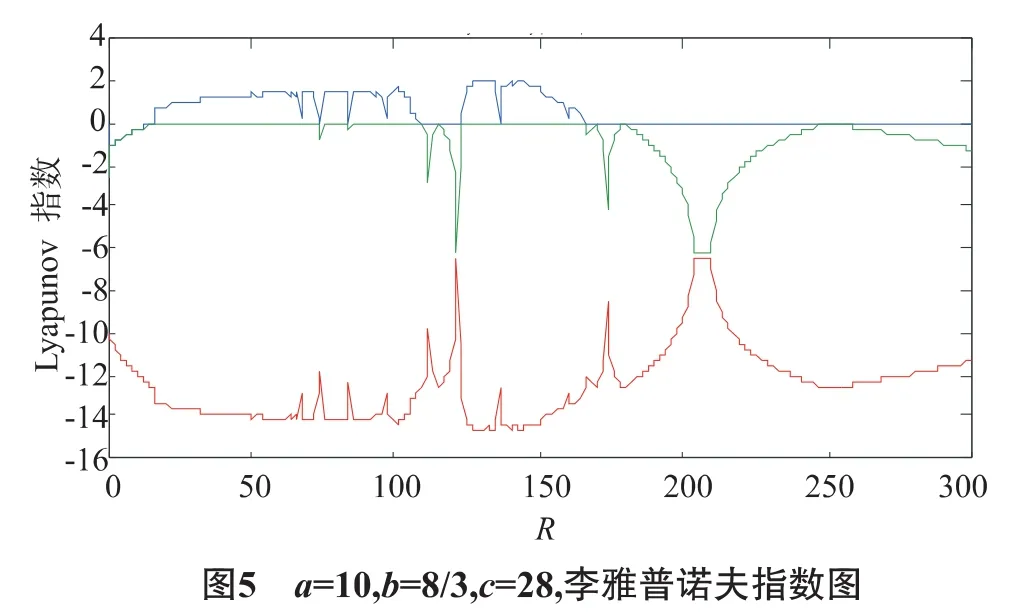
由圖2及圖5可看出，系統(tǒng)在c取0到13時Lyapunov指數(shù)小于0，為一周期運動.在c=13時Lyapunov指數(shù)大于0進入混沌，當c=135時開始作六周期運動，到137開始Hopf分支進入三周期，到151開始Lyapunov指數(shù).

2 數(shù)值仿真

采用四階Runge-Kutta方法數(shù)值模擬求解該方程，使用四階Runge-Kutta方法時，需要先給出初值和步長，系統(tǒng)的初值選取為(0.1，0.1，0.1)，步長選取0.000 1，通過數(shù)值模擬，系統(tǒng)顯示出有豐富的混沌動力學(xué)行為.

1)當參數(shù)a=10，b=8/3，c=28時，對系統(tǒng)(2)發(fā)生分支的數(shù)值仿真.

(a)參數(shù) b=8/3，a=10，改變 c，c∈［0，300］.(如圖2所示)當參數(shù)c在［0，300］變化時，系統(tǒng)(2)的Lyapunov指數(shù)、分支圖如圖2，圖5所示，從Lyapunov指數(shù)譜、分支圖可以比較直觀地反映非線性動力學(xué)系統(tǒng)隨參數(shù)變化的動態(tài)特性.我們知道，只要有一個Lyapunov指數(shù)大于0，系統(tǒng)便處于混沌狀態(tài).

再次大于0進入混沌，到225進入四周期，再經(jīng)過兩次分支，回到單周期運動.

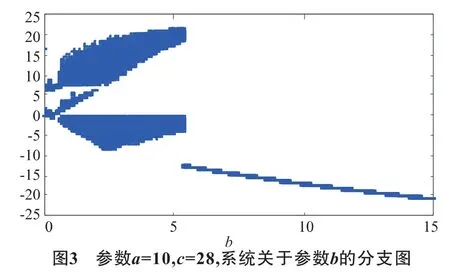
(b)固定參數(shù) a=10，c=28，改變 b，b∈［0，15］.(如圖 3 所示)系統(tǒng)在(0，5.3)為混沌運動，在(5.3，15)之間作單周期運動

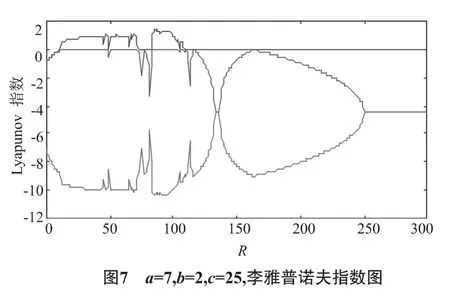
2)取參數(shù) a=7，b=2，c=25，對系統(tǒng)(2)進行分支的數(shù)值仿真(見圖6-9).

固定參數(shù)b與a，對參數(shù)c在(0，300)之間進行分支(如圖6)，當參數(shù)在(0，300)上變化時，由相圖(圖1)知道，其軌線已形成了奇怪吸引子，其截面圖(圖9)上的點不再是少數(shù)離散的，而是由一些密集點連成的弧線，由這些方法所表現(xiàn)的特性可知，系統(tǒng)(2)此時是處于混沌狀態(tài)的.

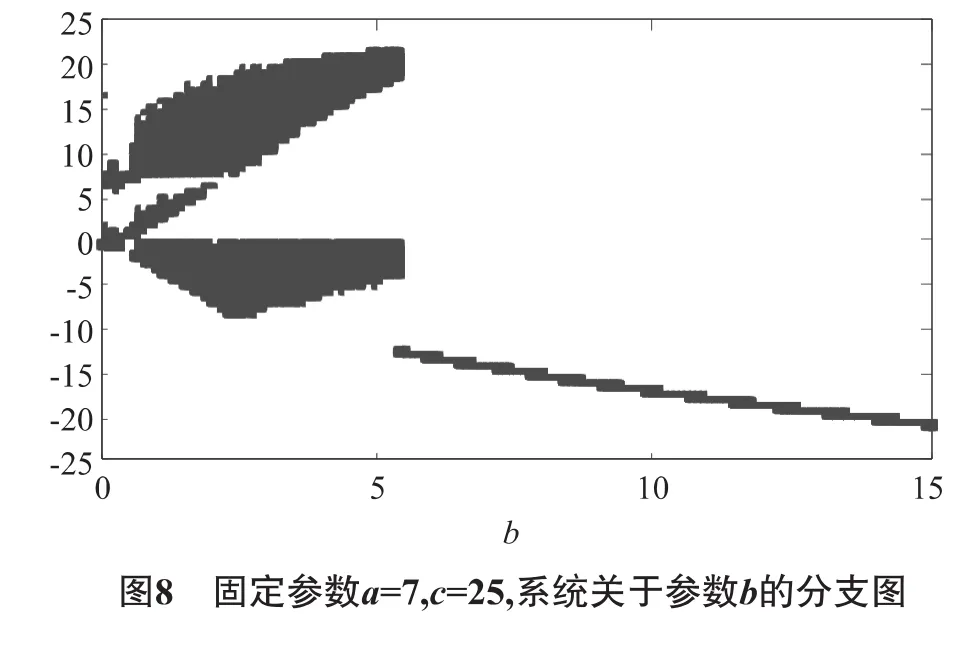
3)選取參數(shù)c為控制參數(shù)時，固定另2個參數(shù)a和b的值，此時系統(tǒng)(2)隨參數(shù) c變化，x方向上的分支圖(如圖8).從圖2中可以看到，參數(shù)c=0是系統(tǒng)(1)發(fā)生平衡點分支的臨界參數(shù)值.當c＜0時，系統(tǒng)(1)沒有平衡點;c=0時，系統(tǒng)(1)只有一個平衡點，即原點;當c＞0時，系統(tǒng)(1)有3個平衡點，它們的坐標分別為O，E1和E2，點H表示Hopf分支臨界點.系統(tǒng)(1)固定(a=10，b=8/3)當參數(shù)c取值逐漸增大，經(jīng)過相應(yīng)的臨界值時，發(fā)生Hopf分支，生成穩(wěn)定極限環(huán)或原有的極限環(huán)消失.參數(shù)取值與推論的結(jié)論相符合，驗證了理論分析的正確性.

3 結(jié)語

本文構(gòu)造了一個三維連續(xù)類Lorenz混沌系統(tǒng)，通過利用非線性動力學(xué)的理論推導(dǎo)得到了系統(tǒng)平衡點穩(wěn)定性及其動力學(xué)行為一些有趣的結(jié)果.選擇不同的參數(shù)值，進一步通過相圖、分支圖、Lyapunov指數(shù)圖、Poincare截面圖研究了系統(tǒng)的混沌運動，得出該系統(tǒng)在不同參數(shù)下的豐富的動力學(xué)行為.

［1］LORENZ E N.Deterministic non-perodic flow［J］.J Atmos Sci，1963(20):130-141.

［2］CHEN G R，UETA T.Yet another chaotic attractor［J］.Inter-national Journal of Bifurcation and Chaos，1999，9(7):1465-1466.

［3］Lü J，CHEN G.A new chaotic attractor coined［J］.International Journal of Bifurcation and Chaos，2002，12(3):659-661.

［4］OSELEDEC V I.A multiplicative ergotic theorem:Lyapunov characteristic numbers for dynamical systems［J］.TransMoscow Math Soc，1968(19):197-231.

［5］ECKMANN J P，RUELLE D.Ergodic theory of chaos and strange attractors［J］.Rev Mod Phys，1985(57):617-656.

［6］WOLF A，SWIFT J，SWINNEY H，et al.Determining Lyapunov exponents from a time series［J］.Physica D，1985，16(3):285-317.

［7］OIWA NN，F(xiàn)IEDLER-FERRARA N.A fast algorithm for estimation Lyapunov exponents from time series［J］.Physics Letters A，1998(246):117-121.

［8］BLAZEJCZYK-OKOLEWSKA B，KAPITANIAK T.Coexisting at-tractors of impact oscillator［J］.Chaos，Solitons and Fractals，1998，9(8):1439-1443.

［9］UDWADIA F E，von BREMEN H F.An efficient stable approach for computaton Lyapunov characteristic exponents of continuous dynamics systems［J］.Appl Math and Computation，2001(121):219-259.

［10］SILVIO L T，de SOUZA I L.Caldas calculation of Lyapunov exponents in systemswith impact［J］.Chaos，Solitons and Fractals，2004(19):569-579.

［11］VENKATESAN A，LAKSHMANAN M.Different routes to chaosvia strange nonchaotic attractors in a quasiperiodically forced system［J］.Physical Review E，1998，58(3):3008-3016.

［12］CHONG G，HAI W，XIE Q.Transient and stationary chaos of a Bose-Einstein condensate loaded into a moving opaticallattice potential［J］.Physical Review E，2004(70):036213.

［13］WEN G L，XU D L.Control algorithm for creation of Hopf bifurcations in continuous time systems of arbitrary dimension［J］.Phys Let A，2005(337):93-100.

［14］JING Z，HUANG J.Bifurcation and chaos in a discrete genetic toggle switch system［J］.Chaos，Solitons and Fractals，2005(23):887-908.

［15］KHALIL H K.Nonlinear Systems［M］.New Jersey:Prentice hall，1996.