PHOTON-SUBTRACTED（-ADDED）THERMO VACUUM STATE AND THEIR APPLICATION IN JACOBI POLYNOMIALS

DA ChengFAN Hong-yi

（1 College of Mechanical and Electronic Engineering，Chaohu College，Chaohu Anhui 238000）

（2 Department of Material Science and Engineering，University of Science and Technology of China，Hefei Anhui 230026）

PHOTON-SUBTRACTED（-ADDED）THERMO VACUUM STATE AND THEIR APPLICATION IN JACOBI POLYNOMIALS

DA Cheng1FAN Hong-yi2

（1 College of Mechanical and Electronic Engineering，Chaohu College，Chaohu Anhui 238000）

（2 Department of Material Science and Engineering，University of Science and Technology of China，Hefei Anhui 230026）

We construct photon-subtracted（-added）thermo vacuum state by normalizing them. As their application we derive some new generating function formulas of Jacobi polynomials，which may be applied to study other problems in quantum mechanics.This will also stimulate the research of mathematical physics in the future.

photon-subtracted（-added）thermo vacuum state；Jacobi polynomials；generating function

1 Introduction

In nature most systems are immersed in a “thermal reservoir”，de-excitation and excitation processes are influenced by the exchange of energy between the reservoir and the system.The presence of the thermal reservoir maintains a certain number of excited quanta.In order to describe the thermal communication between systems and reservoirs more conveniently and the reservoir effect in a natural way，Takahashi and Umezawa invented Thermal Field Dynamics（TFD）theory［1］.

TFD converts the evaluations of ensemble averages at nonzero temperature into equivalent expectation values with a pure state.This worthwhile convenience is at the expense of introducing a fictitious field（or a so-called tilde-conjugate field）.Thus every state〉in the original real field space H is accompanied by a corresponding statein.A similar rule holds for operators：every operator b acting onhas an imageacting on，The thermal vacuum，k is the Boltzmann constant）is defined by the requirement.

Takahashi and Umezawa converted the statistical average at nonzero temperature T into equivalent expectation value with

where H is the Hamiltonian.For single-mode free bosons，H=ωb?b（h=1），the thermal vacuum is constructed as

where S（λ）is called the thermal operator（or thermal transformation，since it engenders the zero temperature vacuum to the thermal vacuum），

and can be disentangled as［2］

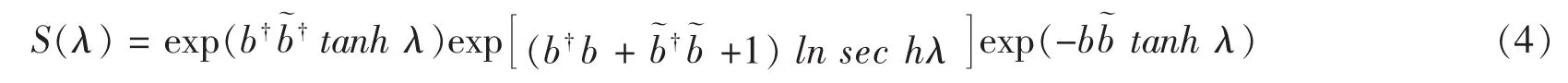
Under the S（λ）transformation，the operator b andbehave as

In the thermal field sense，the parameter λ is related to the number of thermalised photons by

This is in turn given by the Bose-Einstein distribution

Recently，the single-mode photon-subtracted squeezed state（PSSS）have been paid enough attention by both experimentalists and theoreticians due to its non-classical properties.Usually photo-detection for a squeezed light beam will give rise to such a state.In Ref.［3］the problem of what is the compact form of the normalization factor of PSSS has been solved，and the result shows that the normalization factor of PSSS is an r-order Legendre polynomial of the squeezing parameter，where r is the subtracted photon number.

An interesting question naturally arising，as the natural generalization of PSSS，can we construct photon-subtracted thermo vacuum state（PSTVS）and photon-added thermo vacuum state（PATVS）by normalizing them？The answer is affirmative；in Sec 2 we shall employ TFD to construct PSTVS and PATVS.As their applications，in Secs.3 and 4 of this work we shall derive some new generating functions of Jacobi Polynomials by virtue of the PSTVS and PATVS，respectively，which may be useful in studying other quantum mechanical problems.This approach is easier for physicists to accept and may be generalized to derive other special functions′properties，for example，some new properties of Legendre Polynomials can be obtained with the quantum optics method［4］.

2 Construction of PSTVS and PATVS

The thermo vacuum state is given by

In summary，employing TFD we have constructed PSTVS and PATVS，which are the natural generalization of PSSS.In addition，we derive some new generating function formulas of Jacobi Polynomials via an approach in quantum optics theory，i.e.，utilizing PSTVS and PATVS.In turn，these new formulas may be applied to study other problems in quantum mechanics and stimulate the research of mathematical physics in the future.

［1］Takahashi Y.，Umezawa H.Thermo field dynamic［J］.Collect.Phenom.，1975，（2）：55-80.

［2］Umezawa H.，Matsumoto H.Tachiki M.，Thermo field dynamics and condensed states［M］.North-Holland：Amsterdam，1982.

［3］Fan H.Y.，Hu L.Y.，XuX.X.Legendre Polynomials as the Normalization of Photon-Subtracted Squeezed States［J］.Mod.Phys. Lett.A.，2009，（20）：1597-1603.

［4］Zhang Z.X.，F(xiàn)an H.Y.Some Properties of States Engendered by the Excitations on a 2-Mode Squeezed Vacuum State［J］. Phys.Lett.A.，1993，（3）：206-209.

［5］Buzek V.SU（1，1）Squeezing of SU（1，1）Generalized Coherent States［J］.J.Mod.Opt.，1990，（3）：303-316.

［6］Loudon R.，Knight P.L.Squeezed light［J］.J.Mod.Opt.，1987，（34）：709-759.

［7］Wolfgang P.S.Quantum Optics in Phase Space［M］.Berlin：Wiley-VCH，2001.

［8］Glauber R.J.Coherent and Incoherent States of the Radiation Field［J］.Phys.Rev.，1963，（131）：2766-2788.

［9］Fan H.Y.Newton-Leibniz integration for ket-bra operators in quantum mechanics（V）-Deriving normally ordered bivariatenormal-distributionformofdensityoperatorsanddevelopingtheirphasespaceformalism［J］.Ann.Phys.，2008，（6）：1502-1528.

［10］Erdèlyi A.Higher Transcendental Functions，The Bateman Manuscript Project［M］.New York：McGraw Hill，1953.

［11］Abramovitz M.Stegun I.Handbook of Mathematical Functions［M］.New York：Dover Publications Inc，1965.

［12］Fan H.Y.Antinormal Expansion for Rotation Operators in the Schwinger Representation［J］.Phys.Lett.A.，1988，（3）：145-150.

陳 侃

O431.2 Document code：A Article ID：1672-2868（2015）03-0033-07

2014-12-10

Fund Project：Doctoral Scientific Research Foundation of Chaohu College（No.KYQD-201407）

Biography：DA Cheng（1974-），male，born in Tongcheng City，Anhui Province，College of Mechanical and Electronic Engineering，Chaohu College，lecturer，doctor，major in theoretical physics，quantum optics.