線段上連續(xù)非混沌自映射某類點(diǎn)的軌跡

趙 勇

(西華師范大學(xué)數(shù)學(xué)與信息學(xué)院，四川 南充 637009)

一維動(dòng)力系統(tǒng)，特別是線段Ⅰ上的自映射的研究近50年來(lái)發(fā)展迅速，已經(jīng)成為動(dòng)力系統(tǒng)領(lǐng)域中一個(gè)不可忽視的分支．盡管如此，對(duì)線段上自映射迭代的研究，還有很多不完善的地方亟待發(fā)展和突破．其中之一就是“混沌的本質(zhì)是什么［1］”．對(duì)此問(wèn)題，人們已從多個(gè)角度得到了若干充分條件或必要條件［1-8］．本文將在前文［4-5］研究的基礎(chǔ)上，繼續(xù)從?-極限點(diǎn)的軌跡特點(diǎn)來(lái)考慮這一問(wèn)題．文中出現(xiàn)的符號(hào)參見(jiàn)文獻(xiàn)［4］．

1 預(yù)備知識(shí)

引理1［4］設(shè)f 為線段Ⅰ上的連續(xù)自映射，f 的周期點(diǎn)集P(f)不是閉集，則ω(f)-P(f)≠?．

引理2［2］設(shè)f 為線段Ⅰ上的連續(xù)自映射，則以下條件等價(jià):

(1)f 的周期點(diǎn)的周期都是2 的方冪;

(2)對(duì)任意X∈Ω(f)-P(f)，都有ω(X，f)∩P(f)=?;

引理3 設(shè)f 為線段Ⅰ上的連續(xù)自映射，f 的周期點(diǎn)集P(f)不是閉集且只有2 的方冪的周期點(diǎn)，則對(duì)任意的X∈Ω(f)-P(f)，{fn(X)}n=1，2，…，不能為單調(diào)或最終單調(diào)數(shù)列．

證明:根據(jù)引理1，?X∈?(f)-P(f)，下面用反證法證明:假設(shè){fn(X)}為單調(diào)或最終單調(diào)數(shù)列，則必存在m∈N*，使fm(X)，fm+1(X)，fm+2(X)，…為單調(diào)數(shù)列，故必存在f 的不動(dòng)點(diǎn)T，使ω(X，f)={T}，這與引理1 矛盾．

引理4［4］設(shè)f 為線段Ⅰ上的連續(xù)自映射，X∈ω(f)-P(f)，若存在m∈N*，使得:

fm+1(X)＞fm+2(X)＞fm(X)＞fm+3(X)，則f 在Ⅰ上混沌．

引理5［4］設(shè)f 為線段Ⅰ上的連續(xù)自映射，X∈ω(f)-P(f)，若存在m∈N*，使得:

fm+1(X)＜fm+2(X)＜fm(X)＜fm+3(X)，則f 在Ⅰ上混沌．

引理6［6］設(shè)f 為線段Ⅰ上的連續(xù)自映射，X∈ω(f)-P(f)，若存在m∈N*，使得:

fm+3(X)＜fm+2(X)＜fm(X)＜fm+1(X)，則f 在Ⅰ上混沌．

引理7［4］設(shè)f 為線段Ⅰ上的連續(xù)自映射，X∈ω(f)-P(f)，若存在m∈N*，使得:

fm+3(X)＞fm+2(X)＞fm(X)＞fm+1(X)，則f 在Ⅰ上混沌．

引理8［4］設(shè)f 為線段Ⅰ上的連續(xù)自映射，X∈ω(f)-P(f)，若存在m∈N*，使得:

fm+2(X)＜fm+3(X)＜fm(X)＜fm+1(X)，則f 在Ⅰ上混沌．

引理9［4］設(shè)f 為線段Ⅰ上的連續(xù)自映射，X∈ω(f)-P(f)，若存在m∈N*，使得:

fm+2(X)＞fm+3(X)＞fm(X)＞fm+1(X)，則f 在Ⅰ上混沌．

引理10［5］設(shè)f 為線段Ⅰ上的連續(xù)自映射，X∈ω(f)-P(f)，若存在mi∈N*(當(dāng)i→+∞時(shí)，mi→+∞)，使得:fmi(X)＜fmi+3(X)＜fmi+2(X)＜fmi+1(X)，則f 在Ⅰ上混沌．

引理11［5］設(shè)f 為線段Ⅰ上的連續(xù)自映射，X∈ω(f)-P(f)，若存在mi∈N*(當(dāng)i→+∞時(shí)，mi→+∞)，使得:fmi(X)＞fmi+3(X)＞fmi+2(X)＞fmi+1(X)，則f 在Ⅰ上混沌．

2 主要結(jié)論

定理1 設(shè)f 為線段Ⅰ上的連續(xù)自映射，周期點(diǎn)集不閉且f 在Ⅰ上只有2 的方冪的周期點(diǎn)，則對(duì)任意X∈ω(f)-P(f)，orbf(X)具有統(tǒng)一的規(guī)律(見(jiàn)證明結(jié)尾)．

證明:對(duì)?X∈?(f)-P(f)，由引理2 知X 不能為f 的最終周期點(diǎn)，又由引理3 知{fn(X)}n =1，2，…，不能為單調(diào)或最終單調(diào)數(shù)列，從而對(duì)任意的k∈N*，總存在m≥k，使下面16 種情況必有其中之一成立．

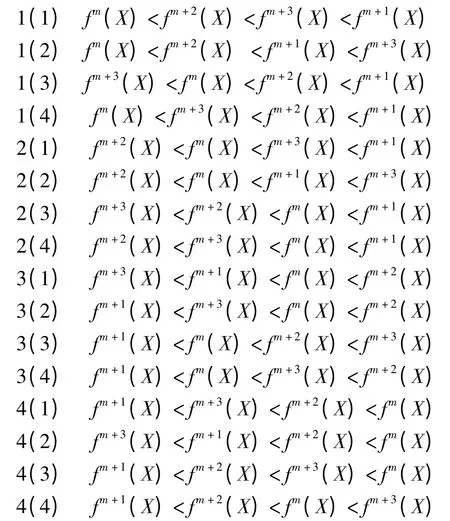
因?yàn)閒 在Ⅰ上只有2 的方冪的周期點(diǎn)，根據(jù)引理4 -11，存在k1∈N*，使得當(dāng)m ＞k1時(shí)，1(1)、1(2)、2(1)、2(2)、3(1)、3(2)、4(1)、4(2)8 種情況必有其一出現(xiàn)無(wú)限次，而1(3)、1(4)、2(3)、2(4)、3(3)、3(4)、4(3)、4(4)一次也不會(huì)出現(xiàn)．

若當(dāng)m ＞k1，情況1(1)出現(xiàn)，則有fm+2(X)＜fm+3(X)＜fm+1(X)，用m 代替m+1 得fm+1(X)＜fm+2(X)＜fm(X)，由于f 在Ⅰ上無(wú)非2 方冪的周期點(diǎn)，則根據(jù)前面的討論，1(1)中迭代指標(biāo)中最大的三項(xiàng)fm+1(X)、fm+2(X)、fm+3(X)之間的大小關(guān)系只能為4(1)或4(2)中迭代指標(biāo)中最小的三項(xiàng)，我們把這種后接關(guān)系記為：

對(duì)1(1)、1(2)、2(1)、2(2)、3(1)、3(2)、4(1)、4(2)中的任一情況出現(xiàn)時(shí)，只能按上面鏈接方式進(jìn)行下去，f在Ⅰ上才可能無(wú)非2 方冪的周期點(diǎn)，在這種鏈接方式下，{fn(X)}n =1，2，…，總是按“遞增然后遞減”或“遞減然后遞增”的規(guī)律無(wú)休止地進(jìn)行下去，即不允許在當(dāng)m ＞k1之后，存在連續(xù)三項(xiàng)具有如下形式:fm(X)＜fm+1(X)＜fm+2(X)或fm(X)＞fm+1(X)＞fm+2(X)，實(shí)際上，對(duì)任意固定的自然數(shù)t，存在正整數(shù)kt∈N*，當(dāng)m＞kt時(shí)，fm(X)、fm+t(X)、fm+2t(X)、fm+3t(X)，…，也有上述當(dāng)t =1 時(shí)的性質(zhì)，即:①具有“* ”標(biāo)明的鏈接關(guān)系;②{fn(X)}的子集{fm+it(X)}，i=0，1，2，…中的點(diǎn)fm+it(X)總是按照i 值遞增的順序嚴(yán)格按照遞增然后遞減”或“遞減然后遞增”的規(guī)律無(wú)休止地進(jìn)行下去;③不會(huì)出現(xiàn)連續(xù)三項(xiàng)具有如下形式:fm(X)＜fm+t(X)＜fm+2t(X)或fm(X)＞fm+t(X)＞fm+2t(X)

現(xiàn)取r=max{k1，k2}，則當(dāng)m ＞r 時(shí)，不會(huì)出現(xiàn)

fm(X)＜fm+2(X)＜fm+4(X)或者fm(X)＞fm+2(X)＞fm+4(X) (* )

現(xiàn)討論1(1)首次出現(xiàn)時(shí)，有以下鏈接關(guān)系:

先看1(1)→4(1):

1(1)為:fm(X)＜fm+2(X)＜fm+3(X)＜fm+1(X)

4(1)為:fm+2(X)＜fm+4(X)＜rm+3(X)＜fm+1(X)

故1(1)→4(1)為:fm(X)＜fm+2(X)＜fm+4(X)＜fm+3(X)＜fm+1(X)，與(* )行矛盾，故1(1)→4(1)不成立．同理可證:4(2)→2(1)、2(2)→3(1)、3(2)→1(2)均不成立．所以，從1(1)開(kāi)始只能按照這樣的鏈接關(guān)系無(wú)限進(jìn)行下去:

1(1)→4(2)→2(2)→3(2)→1(1)→…

若以4(2)首次出現(xiàn)，則有如下鏈接關(guān)系:

4(2)→2(2)→3(2)→1(1)→4(2)→…

若以2(2)首次出現(xiàn)，則有如下鏈接關(guān)系:

2(2)→3(2)→1(1)→4(2)→2(2)→…

若以3(2)首次出現(xiàn)，則有如下鏈接關(guān)系:

3(2)→1(1)→4(2)→2(2)→3(2)→…

同理可證:分別以1(2)、3(1)、2(1)、4(1)為首項(xiàng)的鏈接關(guān)系依次為:

1(2)→3(1)→2(1)→4(1)→1(2)→…

3(1)→2(1)→4(1)→1(2)→3(1)→…

2(1)→4(1)→1(2)→3(1)→2(1)→…

4(1)→1(2)→3(1)→2(1)→4(1)→…

綜上，在定理?xiàng)l件下，對(duì)?X∈?(f)-P(f)，orbf(X)具有這樣的規(guī)律:存在自然數(shù)nx，使得{fn(X)}n =1，2，…，從第nx項(xiàng)開(kāi)始，orbf(X)以:

1(1)→4(2)→2(2)→3(2)→1(1)→…或1(2)→3(1)→2(1)→4(1)→1(2)→…為周期節(jié)無(wú)限鏈接下去．

定理1 揭示了線段上非混沌且周期點(diǎn)集不閉的連續(xù)自映射的點(diǎn)X∈?(f)-P(f)的迭代軌跡的普遍規(guī)律，從另一個(gè)側(cè)面為進(jìn)一步解決混沌的充要條件提供了一個(gè)全新而有效的研究途徑，具有極為重要的作用．后文將在此結(jié)論的基礎(chǔ)上，繼續(xù)進(jìn)行深入研究．

［1］ LITY，YORKE J． Period Three Imply Chaos Amer［J］．Math．monthly，1975，82:985 -992．

［2］ 張景中，熊金城． 函數(shù)迭代與一維動(dòng)力系統(tǒng)［M］．成都:四川教育出版社，1992．187．

［3］ 耿祥義． Li-Yorke 混沌的充要條件［J］．?dāng)?shù)學(xué)學(xué)報(bào)，2001，44(5):985 -992．

［4］ 趙 勇． 線段上連續(xù)自映射混沌現(xiàn)象的幾個(gè)充分條件［J］．四川師范學(xué)院學(xué)報(bào)(自)．2002，23(4):342 -344．

［5］ 趙 勇． 線段上連續(xù)自映射混沌現(xiàn)象的幾個(gè)充分條件二［J］．西華師范大學(xué)學(xué)報(bào)(自)．2003，24(4):335 -337

［6］ 趙 勇． 射混映射下周期點(diǎn)集的性質(zhì)［J］． 四川師范學(xué)院學(xué)報(bào)(自)．2000，20(1):25 -30．

［7］ 周作領(lǐng)． 一維動(dòng)力系統(tǒng)［J］．?dāng)?shù)學(xué)季刊．1988．3(1):42 -64．

［8］ 熊金城．線段映射的動(dòng)力體系:非游蕩集，拓?fù)潇丶盎靵y．?dāng)?shù)學(xué)進(jìn)展，1988．17(1):1 -11．