連續分度冷滾打機床滾打頭結構改進

馬群，李言，楊明順，袁啟龍，李玉璽

（1.西安理工大學機械與精密儀器工程學院，陜西西安710048；2.西安工業大學光電工程學院，陜西西安710021）

連續分度冷滾打機床滾打頭結構改進

馬群1，2，李言1，楊明順1，袁啟龍1，李玉璽1

（1.西安理工大學機械與精密儀器工程學院，陜西西安710048；2.西安工業大學光電工程學院，陜西西安710021）

采用連續分度方式冷滾打花鍵時滾打輪和工件間存在一個干涉運動，實際生產中將機床滾打頭部分整體傾斜一個安裝角以減小干涉量。在安裝角作用下，滾打輪成形輪廓發生變化，帶來新的成形誤差。分析了干涉現象產生的原理，設計了改進的滾打頭結構，利用斜銅套將滾打輪自轉軸反向傾斜一個安裝角，使滾打輪成形輪廓不變。建立了計算滾打輪在鍵槽截面上成形曲線的數學模型，利用鍵槽寬度誤差對冷滾打成形誤差進行了表征。當冷滾打機床采用現有滾打頭結構時，設置安裝角雖然提高了成形精度，仍存在較大的成形誤差；采用改進的滾打頭結構時，安裝角在一定范圍內取值，干涉量和滾打頭傾斜帶來的成形誤差均減小為0 mm.改造機床滾打頭部分進行冷滾打實驗，精確測量了試樣鍵槽輪廓，結果表明：不設置安裝角時，鍵槽寬度誤差的實測值與理論計算相符；設置安裝角時，鍵槽寬度誤差的實測值及其相對變化量都很小。實驗驗證了改進的滾打頭結構的合理性。

機械制造工藝與設備；結構改進；成形誤差；干涉現象；安裝角

0 引言

漸開線花鍵具有傳動平穩、對中性好、起動承載能力大和傳遞轉矩大等優點，廣泛應用于軍工、機床、汽車、拖拉機、航空和航天等行業中［1］。花鍵冷滾打（又稱為冷打或冷滾敲）是一種精密冷體積成形技術，具有加工效率高和材料利用率高等優點［2-5］。早在20世紀70年代，瑞士、美國、日本和德國等國就相繼研制了花鍵和齒輪冷滾打設備并投入生產［6］。國內研究主要集中在兩個階段：20世紀80年代以前，我國多家生產單位引進了國外的冷滾打設備并展開研究，但主要是以生產試制和實驗摸索為主，沒有深入地了解冷滾打成形機理，因此一直以來主要配件仍依賴進口，相關設計資料和軟件也是由國外提供［7-8］；近年來，冷滾打成形技術重新受到許多科研單位的關注，西安理工大學和河南科技大學在滾打輪設計、冷滾打成形機理研究、冷滾打結構動力學特性和金屬微觀組織等方面做了深入研究［3-5，8-9］。

冷滾打加工通過一對輪廓與花鍵齒槽形狀相同的滾打輪對工件不斷擊打，使工件產生塑性變形從而形成合格的花鍵齒［6］。花鍵冷滾打分度方式有連續分度和間歇分度兩種，采用間歇分度的機床機構復雜、剛度差，容易產生沖擊和振動，目前大部分設備均采用連續分度的方式。雖然滾打輪擊打工件一次的作用時間很短（小于1ms），但由于工件連續分度，滾打輪與工件間存在一個干涉運動，降低了成形精度。為使分度運動不影響成形后的齒形，實際生產中將機床滾打頭部分整體傾斜一個角度（安裝角），使滾打輪在擊打工件時產生與工件自轉運動趨勢相同的速度，減小干涉量。文獻［6，9-10］給出了安裝角的計算原理，雖然通過設置安裝角大大提高了花鍵的成形精度，但依然存在許多問題：首先，偏轉一個角度后，滾打輪的成形輪廓發生了變化，帶來了新的成形誤差，通過輪廓修形的方法進行改進又十分困難，目前國內生產廠家尚未完全掌握這項技術；其次，安裝角數值一般很小（幾個毫弧度），分度頭很難保證設置精度；再次，考慮到加工過程中金屬的塑性流動和工件材料的彈性恢復，滾打輪輪廓設計還需要大量分析、模擬和實驗工作進行修正，應盡可能避免此誤差帶入下一環節，影響進一步研究。

本文根據漸開線花鍵冷滾打的累積成形原理，分析干涉現象產生的原因，針對機床滾打頭傾斜帶來的成形誤差，設計改進的滾打頭結構，建立數學模型計算采用改進的滾打頭結構時冷滾打成形誤差，改造現有冷滾打機床進行實驗，驗證了改進滾打頭結構的合理性。

1 連續分度冷滾打花鍵的原理

圖1給出了連續分度冷滾打花鍵的原理，建立直角坐標系，以工件的軸為z軸，以滾打輪輪廓線的對稱軸為y軸。兩滾打輪嚴格同步反向回轉，角速度為ωg，滾打輪每回轉一周擊打工件一次。工件以角速度ωp連續分度自轉，同時又以速度v沿工件軸向進給。兩滾打輪在與工件接觸的時間段內，受摩擦力作用在工件上滾動，角速度為ωr.機床傳動系統嚴格保證ωg與ωp的比值為花鍵齒數，由此便加工出與滾打輪輪廓吻合的漸開線鍵槽。

圖1 連續分度冷滾打花鍵的原理Fig.1 Schematic diagram of spline continuous indexing cold roll-beating

2 滾打頭傾斜帶來的成形誤差

2.1 連續分度冷滾打的干涉現象

圖2給出了工件某一鍵槽截面的成形過程。假設冷滾打過程中工件不做分度運動，當滾打輪位于工件某一鍵槽截面A處時，此鍵槽截面的成形過程開始，工件進給速度為v（mm/r）.在鍵槽截面A的下一個冷滾打過程，工件自轉了一周，截面A移動至截面A1處，則滾打輪到達該截面時多回轉了一個角度θ1：

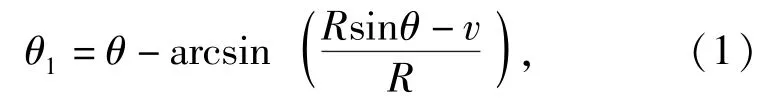
圖2 工件某一鍵槽截面的成形過程（ωp=0）Fig.2 Forming process of a keyway section of workpiece（ωp=0）

此時滾打輪形成的鍵槽深度為

則在此鍵槽截面的第i（i=2，3，…，n）個冷滾打過程，滾打輪到達該截面時多回轉的角度為

滾打輪形成的鍵槽深度為

隨著工件的連續進給，當鍵槽截面A移動至截面An處（到達滾打輪回轉中心正下方）時，鍵槽深度ln=h，此鍵槽截面成形過程結束，則截面An處為該鍵槽截面的成形位置。在此后的冷滾打過程中，滾打輪與此鍵槽截面不再產生作用關系。因此，工件鍵槽輪廓與滾打輪輪廓吻合，滾打輪與工件不發生干涉。

但在實際加工過程中，工件具有一個連續分度的角速度ωp，在鍵槽截面A成形過程開始后的第i個冷滾打過程，工件同時多回轉了一個角度θi/z（z為花鍵的齒數），即工件鍵槽輪廓相對滾打輪發生了偏轉，這樣滾打輪與工件之間便產生了干涉現象。當冷滾打形成的鍵槽深度較小時，這個干涉量可不考慮，因為寬度不斷增大的鍵槽將覆蓋這個干涉量；當形成的鍵槽深度接近h時，鍵槽的寬度變化越來越小，干涉量便影響到了鍵槽的成形。另外，在鍵槽截面A經過成形位置后的頭幾個冷滾打過程中，由于工件的連續分度，滾打輪仍對工件產生作用，這也導致干涉現象。

2.2 滾打頭傾斜帶來的成形誤差

為使分度運動不影響工件的齒形，將滾打頭部分整體傾斜一個安裝角β，其計算方法與單頭滾刀的螺旋升角相似，可由（5）式確定［6，9-10］：

式中：m為花鍵模數；D為滾打輪齒形部分外圓回轉直徑，D=2×（R+r）.

安裝角設定后，滾打輪在回轉運動時具有與工件分度運動趨勢相同的速度，減小了干涉量，但其成形輪廓發生了變化，如圖3所示。

圖3 滾打輪成形輪廓寬度的變化情況Fig.3 Change of width of roller forming profile

圖3中，w為滾打輪在一定齒高處的成形輪廓寬度，w′為滾打頭傾斜安裝角β后在相同齒高處的成形輪廓寬度，可見滾打輪成形輪廓寬度發生了變化，若要分析其寬度的變化情況，需建立滾打輪輪廓曲面數學模型。

如圖1所示，滾打輪輪廓曲線包括兩處沿y軸對稱的漸開線、一處齒根圓弧和兩處過渡圓弧五部分［11］。

漸開線方程為

式中：φb為漸開線展角；rb為基圓半徑；α為花鍵壓力角。

將漸開線旋轉至圖1所示的鍵槽輪廓上，則

式中：Rw為角度θz的旋轉變換矩陣；θz=π/2+π/z.

另外一側的漸開線為

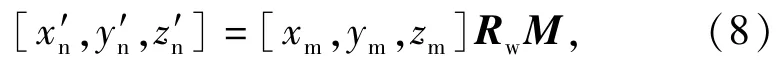
式中：M為沿y軸的對稱變換矩陣。

齒根圓方程為

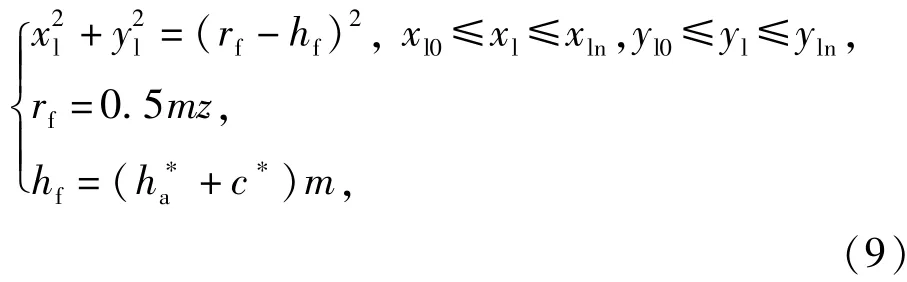
式中：rf為分度圓半徑；hf為齒根高；為齒頂高系數；c*為頂隙系數；（xl0，yl0）和（xln，yln）分別為齒根圓弧與兩側過渡圓弧的交點。

一側的過渡圓弧曲線方程為

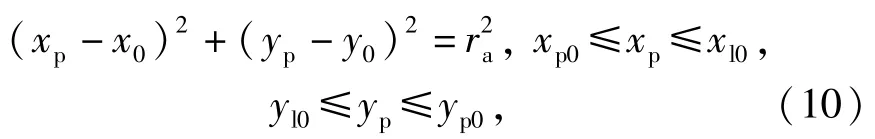
式中：ra為過渡圓弧半徑，一般取ra=0.5 mm；（x0，y0）為過渡圓弧的圓心；（xp0，yp0）為過渡圓弧與漸開線的交點。

另一側過渡圓弧曲線方程為

則整個滾打輪輪廓曲線上的點可表示為

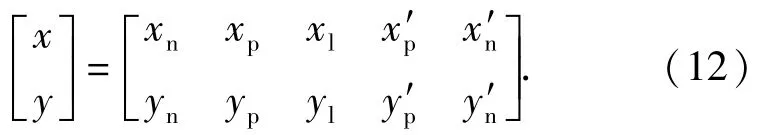
滾打輪軸的參數方程可表示為

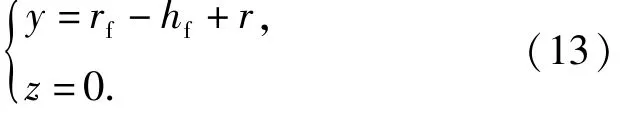
對（12）式確定的點繞滾打輪軸旋轉一周，可得滾打輪輪廓曲面上的點：

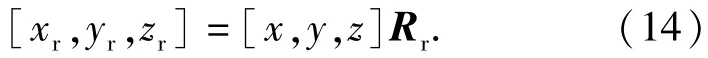
式中：Rr為漸開線曲線繞滾打輪軸的旋轉變換矩陣。

若滾打頭整體傾斜一個安裝角β，則其輪廓曲面上的點變為

式中：Ry為角度β的漸開線曲線繞y軸的旋轉變換矩陣。

冷滾打參數定義為：m=2，z=20，α=20°，r= 20 mm，R=100 mm.帶入（5）式～（15）式進行計算。

由（5）式得安裝角β=0.008 3 rad.

表1給出了不同齒高處滾打輪成形輪廓寬度的變化情況。從表1可以看出：在安裝角作用下，滾打輪成形輪廓寬度增大。

表1 滾打輪成形輪廓寬度的變化情況Tab.1 Change of width of roller forming profile

若按花鍵齒形設計滾打輪輪廓，將導致成形誤差。對滾打輪輪廓修形可提高成形精度，但輪廓修形工作十分復雜，國內尚未完全掌握這項技術，并且加工不同參數花鍵的滾打輪都要進行輪廓修形，消耗大量的人力、物力。

3 改進的滾打頭結構

圖4給出了現有冷滾打機床滾打頭部分結構［6，10，12］，滾打軸旋轉帶動滾打輪繞其軸OO′回轉，滾打輪與半圓銅套形成滑動軸承副。當滾打軸傾斜一個安裝角β時，滾打輪也傾斜同樣的角度，這樣滾打輪對工件的接觸狀態由正接觸變為斜接觸，成形輪廓發生變化。

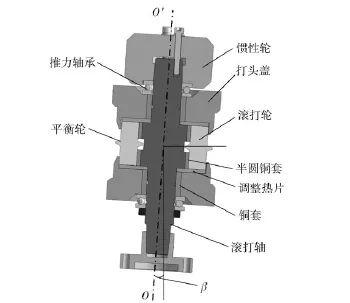
圖4 現有滾打頭部分結構Fig.4 The existing structure of roll-beating head

圖5給出了改進的滾打頭部分結構，滾打輪和斜銅套形成滑動軸承副，雖然滾打軸偏轉一個安裝角β，但滾打輪上下兩端的斜銅套剛好使其向相反的方向偏轉角度β.這時，滾打軸偏轉一個安裝角，不僅滾打輪在回轉運動時產生了一個與工件自轉趨勢相同的速度，減小了干涉量，而且滾打輪對工件的接觸狀態和成形輪廓未發生變化，避免了滾打頭傾斜帶來的成形誤差。

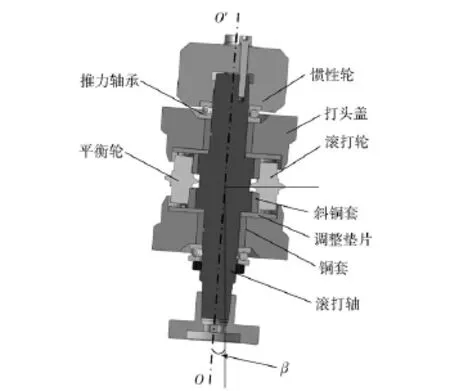
圖5 改進的滾打頭部分結構Fig.5 The improved structure of roll-beating head

4 成形誤差分析

分析冷滾打成形誤差時暫不考慮工件材料的彈性恢復、機床的振動和傳動系統誤差等因素。

4.1 滾打輪成形曲線數學模型

先分析工件某鍵槽截面經過成形位置后的冷滾打過程。

如圖2所示，假設工件某鍵槽截面A位于截面An處，則在下一個冷滾打過程中，工件移動一個進給量的值p=1×v=v（mm），滾打輪運動至截面A時多回轉了一個角度φ1：

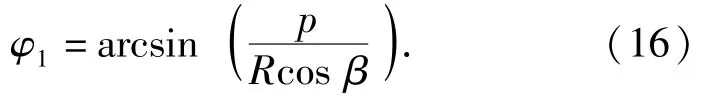
假定工件靜止不動，考慮到工件的連續分度運動，相當于由（12）式確定的點［x，y］繞z軸沿工件分度運動的反方向旋轉一個角度γ1=φ1/z，并沿y軸正向平移σ1=R（1-cosφ1），另外在安裝角作用下，沿x軸負方向平移τ1=Rsinφ1sinβ，即

式中：Rz1為角度γ1的滾打輪成形曲線繞z軸的旋轉變換矩陣。

因此，在經過截面An后的第i（i=2，3，…，n）個冷滾打過程中，滾打輪運動至截面A時其輪廓曲線上的點為

式中：σi=R（1-cosφi）；τi=Rsinφisinβ；Rzi為角度γi的滾打輪成形曲線繞z軸的旋轉變換矩陣，γi= φi/z，φi可由（19）式確定：

按上述方法，可推導出：在經過截面An之前的第j（j=1，2，3，…，n）個冷滾打過程中，滾打輪運動至截面A時其輪廓曲線上的點為

式中：σj=σi；τj=-τi；Raj為滾打輪成形曲線繞z軸的旋轉變換矩陣，方向與Rzi相反。

設v=1.3 mm/r，由（5）式～（20）式確定滾打輪在工件鍵槽截面上的成形曲線，其中齒根簡化為一段直線。

4.2 成形誤差分析

圖6給出了工件鍵槽截面上滾打輪的成形曲線（β=0 rad），其中鍵槽寬方向為x.從圖6可以看出：1）干涉現象是由多次冷滾打累積形成的，鍵槽成形輪廓曲線是滾打輪在冷滾打過程的包絡線，因此漸開線花鍵冷滾打具有展成法的特點；2）在齒高h為0.3～1.0 mm范圍內干涉現象最為明顯，因過渡圓弧ra=0.5 mm，則包括過渡圓弧和漸開線的一部分；3）在齒高0.3～1.0 mm范圍內鍵槽輪廓齒面波紋度較大。

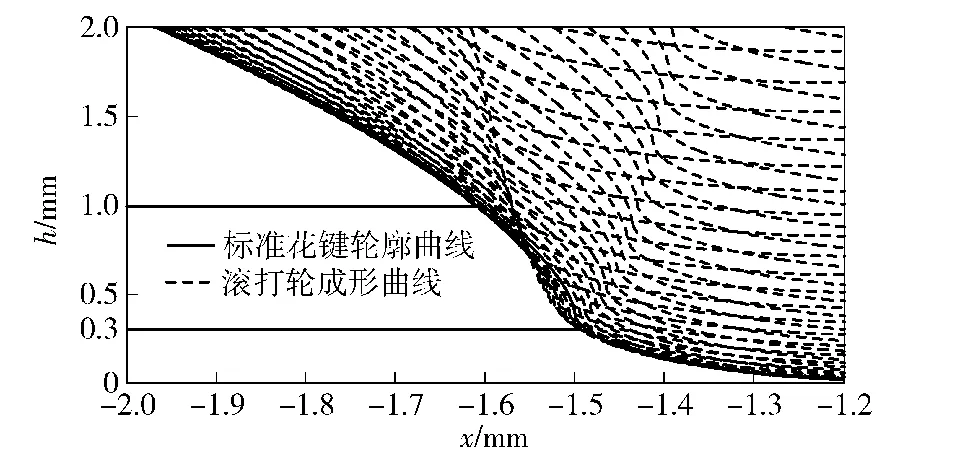
圖6 工件鍵槽截面上滾打輪的成形曲線（β=0 rad）Fig.6 Forming curves of roller on the keyway section of workpiece（β=0 rad）

將冷滾打成形的鍵槽輪廓曲線與標準鍵槽輪廓曲線進行對比，可計算出不同齒高處的鍵槽寬度誤差和整個鍵槽輪廓的平均鍵槽寬度誤差，本文利用這兩個物理量表征漸開線花鍵冷滾打的成形誤差。

圖7給出了采用現有滾打頭結構時鍵槽寬度誤差e沿齒高h的分布情況。由于過渡圓弧部分不影響嚙合，只對漸開線部分的鍵槽寬度誤差進行計算。由圖7可知：1）不論安裝角設置與否，鍵槽寬度誤差均為正值，如不對滾打輪輪廓做幾何修形，則鍵槽成形輪廓略大；2）不設置安裝角時，成形誤差在漸開線的起始位置（h為0.5～1.0 mm）處最大，約為0.08 mm，并沿齒高方向不斷減小；3）滾打頭傾斜一個安裝角后，成形誤差雖然得到了控制，但仍然存在，這是滾打輪成形輪廓變化所導致的；4）在漸開線起始位置處，成形誤差出現波動，這說明此處齒面波紋度較大。

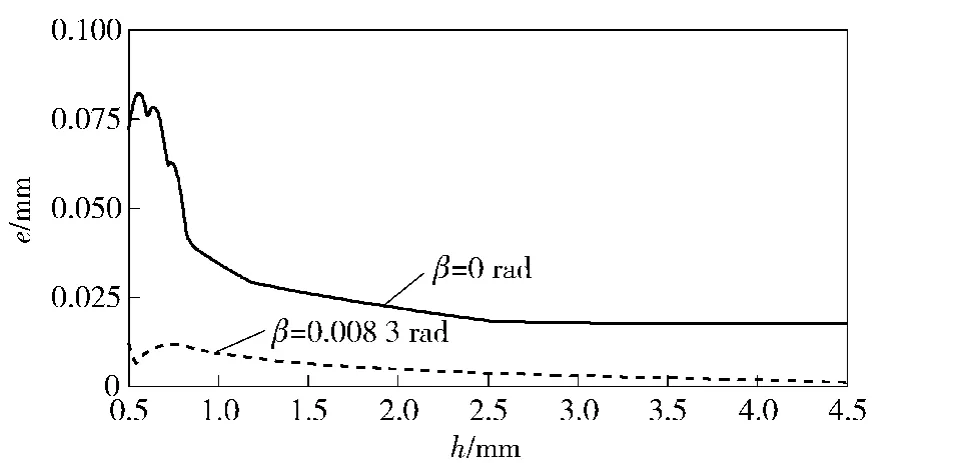
圖7 鍵槽寬度誤差沿齒高的分布情況Fig.7 Distribution of keyway width errors along the tooth depth

采用改進的滾打頭結構時，不能由（5）式確定滾打輪的安裝角，本文不斷改變β值并計算不同β值下鍵槽輪廓的平均鍵槽寬度誤差，從而得到成形誤差最小時的β值。

圖8給出了采用改進的滾打頭結構時平均鍵槽寬度誤差eq隨安裝角β的變化情況。由圖8可以看出：平均鍵槽寬度誤差隨安裝角的增大呈先減小后增大的趨勢，并在一個安裝角范圍內達到最小值0 mm.進一步計算可知：當安裝角為0.008 5～0.009 7 rad時，平均鍵槽寬度誤差均為0 mm.但僅由圖8及其計算結果尚無法確定采用改進滾打頭結構時的成形誤差，因鍵槽寬度誤差的平均值為0 mm，不能證明不同齒高處的鍵槽寬度誤差都為0 mm.

圖9給出了采用改進的滾打頭結構時工件某鍵槽截面上滾打輪的成形曲線（β=0.009 1 rad）。由圖9可以看出：1）在成形過程中，整個鍵槽輪廓均未發生干涉現象，成形輪廓與標準鍵槽輪廓很好地吻合；2）漸開線起始位置處的齒面波紋度被很好地消除；3）過渡圓弧部分也未出現干涉現象。

圖8和圖9的結果表明：1）改進的方法不僅消除了干涉量帶來的成形誤差，還消除了滾打頭傾斜帶來的成形誤差；2）采用改進的滾打頭結構時，可以找到一個安裝角取值范圍，使干涉量和滾打頭傾斜帶來的成形誤差都為0 mm；3）采用改進的滾打頭結構時，漸開線花鍵冷滾打具有了成形法的特點，而不是展成法。

在生產中，可選擇理論計算安裝角取值范圍的中間值（0.009 1 rad），即使有少量安裝角設定誤差，亦能保證加工精度。

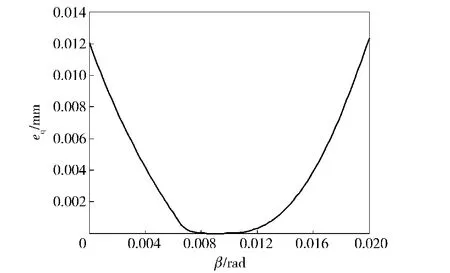
圖8 平均鍵槽寬度誤差隨安裝角的變化情況Fig.8 Change of average keyway width errors with setting-angles

圖9 采用改進滾打頭結構時滾打輪成形曲線（β=0.009 1 rad）Fig.9 Forming curves of roller with improved structure of roll-beating head（β=0.009 1 rad）

5 實驗驗證

為驗證理論分析及仿真結果的正確性，改造冷滾打機床的滾打頭結構并進行原理實驗，實驗參數定義為：ωg=104 rad/s，ωp=5.2 rad/s，m=2，z= 20，α=20°，v=1.3 mm/r.未設置安裝角時滾打輪兩端為半圓銅套，設置安裝角時滾打輪兩端為斜銅套，分別進行實驗，得到冷滾打試樣如圖10所示。

利用海克斯康global三坐標測量儀對試樣鍵槽輪廓進行測量，漸開線部分取30個點，計算得到試樣鍵槽寬度誤差沿齒高的分布情況，如圖11所示。當安裝角為0 rad時，鍵槽寬度誤差均為正值，在漸開線起始位置處最為明顯，約為0.08 mm，自漸開線起始位置沿齒高方向向上，鍵槽寬度誤差減小至0.03 mm左右，與仿真結果相符；當安裝角為0.009 1 rad時鍵槽寬度誤差很小，并有正值和負值，且負值居多，這是由金屬塑性變形后的彈性恢復導致的，自漸開線起始位置向上，鍵槽寬度誤差的變化量很小。

圖10 冷滾打試樣Fig.10 Cold roll-beating samples

圖11 試樣鍵槽寬度誤差沿齒高的分布情況Fig.11 Distribution of keyway width errors of samples along tooth depth

實驗結果證明了采用改進的滾打頭結構時，消除了干涉量和滾打頭傾斜帶來的成形誤差。

6 結論

1）將滾打頭傾斜一個安裝角減小了干涉量，但滾打輪成形輪廓發生了變化，引入了新的成形誤差。

2）設計了改進的滾打頭結構，采用斜銅套確保滾打輪對工件的正接觸狀態。

3）通過數值模擬，計算了采用改進的滾打頭結構時安裝角工藝值為0.008 5～0.009 7 rad（m=2，z=20，α=20°，R=100 mm），當安裝角在工藝值范圍內取值時干涉量和滾打頭傾斜帶來的成形誤差均減小為0 mm.

4）改造設備進行了冷滾打實驗，對實驗結果進行了對比和分析，驗證了改進的滾打頭結構的合理性。

（

）

［1］劉志奇，宋建麗，李永堂，等.漸開線花鍵冷滾壓精密成形工藝分析及試驗研究［J］.機械工程學報，2011，47（14）：32-38. LIU Zhi-qi，SONG Jian-li，LI Yong-tang.Analysis and experimental study on the precision cold rolling process of involute spline［J］.Journal of Mechanical Engineering，2011，47（14）：32-38.（in Chinese）

［2］Klepikov V V，Bodrov A N.Precise shaping of spline shafts in automobile manufacturing［J］.Russian Engineering Research，2003，23（12）：37-40.

［3］崔鳳奎，李言，周彥偉，等.漸開線花鍵滾軋輪建模及其修正［J］.南京航空航天大學學報，2005，37（S）：90-93. CUI Feng-kui，LI Yan，ZHOU Yan-wei，et al.Roller modeling for involute spline and its amendment［J］.Journal of Nanjing University of Aeronautics&Astronautics，2005，37（S）：90-93.（in Chinese）

［4］楊建璽，崔鳳奎，王曉強，等.冷滾軋滾輪設計理論及實驗修正［J］.中國機械工程，2004，15（24）：2168-2171. YANG Jian-xi，CUI Feng-kui，WANG Xiao-qiang，et al.Design theory and experimental amends of involute spline roller［J］.China Mechanical Engineering，2004，15（24）：2168-2171.（in Chinese）

［5］崔鳳奎，李言.漸開線花鍵滾軋CAD及磨削仿真［J］.機械工程學報，2005，41（12）：210-215. CUI Feng-kui，LI Yan.CAD system of roller for involute spline and simulation of grinding process［J］.Journal of Mechanical Engineering，2005，41（12）：210-215.（in Chinese）

［6］林苗興.冷打花鍵工藝［J］.拖拉機，1989（4）：36-41. LIN Miao-xing.Process for cold beating spline［J］.Tractor，1989（4）：36-41.（in Chinese）

［7］葛便京，楊有亮，馮春英，等.漸開線花鍵軸冷滾軋輪的設計［J］.工具技術，1998，32（12）：24-26. GE Bian-jing，YANG You-liang，FENG Chun-ying，et al.Design of cold rolling tools for involute splined shafts［J］.Tool Engineering，1998，32（12）：24-26.（in Chinese）

［8］崔鳳奎，朱文娟，王曉強，等.高速冷滾打成形技術研究現狀與發展趨勢［J］.河南理工大學學報：自然科學版，2012，31（2）：191-200. CUI Feng-kui，ZHU Wen-juan，WANG Xiao-qiang，et al.Current research and development trends of high-speed cold rolling technology［J］.Journal of Henan Polytechnic University：Natural Science，2012，31（2）：191-200.（in Chinese）

［9］崔鳳奎.高速精密冷滾打成形技術研究［D］.西安：西安理工大學，2007. CUI Feng-kui.Study of high-speed precise forming with cold rollbeating technique［D］.Xi'an：Xi'an University of Technology，2007.（in Chinese）

［10］廣州拖拉機廠.冷打花鍵軸工藝［J］.機械科技動態，1976（1）：1-12. Guangzhou Tractor Factory.Process for cold beating spline shaft［J］.Developments in Mechanical Science and Technology，1976（1）：1-12.（in Chinese）

［11］彭樹杰，彭劭聞.漸開線圓柱齒輪體積的算法研究［J］.模具技術，2011（6）：1-4. PENG Shu-jie，PENG Shao-wen.Algorithms research on tooth profile volume of involute profile cylindrical part［J］.Die and Mould Technology，2011（6）：1-4.（in Chinese）

［12］Ernst G，Krapfenbauer H.Roller head for cold roiling of splined shafts or gears：United States，3818735［P］.1973-04-23.

Structure Improvement of Roll-beating Head
for Continuous Indexing Cold Roll-beating Machine

MA Qun1，2，LI Yan1，YANG Ming-shun1，YUAN Qi-long1，LI Yu-xi1
（1.School of Mechanical and Precision Instrument Engineering，Xi'an University of Technology，Xi'an 710048，Shaanxi，China；2.School of Photoelectrical Engineering，Xi'an Technological University，Xi'an 710021，Shaanxi，China）

Movement interference between roller and workpiece appears during continuous indexing cold roll-beating of involute spline.The rotary shaft of roller can be tilted at a setting-angle to reduce the interference.The forming profile of roller changes to cause new forming errors under the action of setting-angle.The principle of interference is analyzed，and the improved structure of roll-beating head is designed.The roller is inclined in the opposite direction at a setting-angle by an inclined copper bearing，which ensures the forming profile of roller.A mathematic model is established for calculating the forming profile curves of roller on the keyway section，and the forming errors are characterized by keyway width errors.The forming errors are still large when the existing structure of roll-beating head is used，although the forming accuracy is improved under the action of setting-angle.The interference and the forming errors brought by the inclination of roll-beating head are eliminated in a suitable range of setting-angles when the improved structure of roll-beating head is used.The roll-beating head is improved for cold roll-beating experiment.The keyway profiles of samples are precisely measured.The result indicates that the measured values of keyway width errors are consistent with the theoretical values without the action of setting-angle，and the measured values of keyway width errors and their relative variations are both very small under the action of setting-angle.

manufacturing technology and equipment；structure improvement；forming error；interference；setting-angle

TG66

A

1000-1093（2015）08-1587-07

10.3969/j.issn.1000-1093.2015.08.030

2014-09-24

國家自然科學基金項目（51075124、51475366）；高等學校博士學科點專項科研基金項目（20116118110005）

馬群（1979—），男，博士研究生。E-mail：maqun21@xina.com；李言（1960—），男，教授，博士生導師。E-mail：ly-jyxy@xaut.edu.cn