爆轟驅動金屬圓筒的能量轉換與破片初速模型

王新穎，王樹山，徐豫新，胡賽

（北京理工大學機電學院，北京100081）

爆轟驅動金屬圓筒的能量轉換與破片初速模型

王新穎，王樹山，徐豫新，胡賽

（北京理工大學機電學院，北京100081）

基于爆轟產物的JWL狀態方程和Taylor破裂判據，從能量守恒出發推導了一種考慮膨脹細節的爆轟驅動金屬圓筒能量轉換與破片初速模型。選用無氧銅、45#鋼和6061鋁合金3種材料進行壓裝TNT炸藥驅動的圓筒試驗。對比試驗的膨脹軌跡與膨脹速度和模型計算結果，表明所建立的爆轟驅動模型綜合考慮了炸藥-金屬系統驅動的膨脹過程和力學性能因素，相比格尼公式只單一考慮炸藥爆轟參數的驅動能力，更全面地考慮爆轟驅動影響因素，計算結果更具有針對性和適用性。

兵器科學與技術；爆轟驅動；狀態方程；能量轉換；破片初速

0 引言

炸藥作為常規武器毀傷的毀傷能源，爆轟驅動金屬加速能力一直是常規武器設計研發所關心的重要問題。炸藥驅動金屬加速能力主要體現為金屬破片的動能，即破片初速。廣泛適用性的計算破片初速的方法是Gurney等［1］提出的格尼公式。假定爆轟前炸藥裝藥的化學能直接轉化為爆轟后的金屬動能和爆轟產物的膨脹，這種能量稱為格尼能。雖然格尼能在某種程度上反應了炸藥對物體的驅動能力，但從各經驗公式［2-4］上可以看出，格尼能均單一從炸藥的爆轟參數考慮，并沒有考慮膨脹過程中爆轟產物膨脹規律的影響，也沒有考慮驅動的金屬對膨脹過程的影響，不同的膨脹過程對金屬做功的驅動能力是不同的。爆轟驅動過程的本質是能量轉換，理想炸藥瞬時定容爆轟，釋放出的化學能以爆轟產物為載體，通過爆轟產物的膨脹，不斷轉化為爆轟產物的能量和驅動破片的能量，用于驅動金屬的能量只占炸藥釋放總能量的一部分，甚至是一小部分，故計算破片初速既和炸藥的性質有關，又和爆轟產物膨脹過程有關，也與作用環境與介質有關。

Kennedy等［5］運用爆轟產物的γ定律狀態方程擴展了格尼方程，討論了對稱平板夾層裝藥驅動飛片的速度。對爆轟驅動金屬加速運動的破裂機理和準則方面也有大量的研究［6-8］。金屬圓筒的損傷與破壞不僅與載荷強度、加載方式和幾何結構有關，而且與材料的物理力學等特性有關，較為經典的是Taylor判據。本文從能量守恒出發，基于爆轟產物的JWL狀態方程和Taylor破裂判據，提出爆轟產物驅動金屬圓筒的能量轉換和破片初速模型，通過對比分析同一結構下的3種金屬的圓筒驅動試驗膨脹軌跡和破片初速，討論爆轟產物膨脹過程對驅動金屬加速運動的影響因素。

1 爆轟驅動模型

本模型建立基于以下假設：1）炸藥瞬時定容爆轟，不考慮爆轟過程中的能量耗散，且忽略驅動過程中的金屬變形能和空氣沖擊波能；2）爆轟產物膨脹遵循JWL狀態方程，金屬圓筒在爆轟產物作用下僅做徑向運動，且徑向膨脹速度呈線性分布；3）爆轟產物在圓筒內分布均勻，即密度為常數；4）金屬圓筒破裂遵循Taylor破裂準則。

基于能量守恒，根據假設1，炸藥的化學能全部轉化為爆轟產物氣體的內能，隨著爆轟產物的膨脹做功逐漸轉換為爆轟產物動能和金屬圓筒的動能，故有

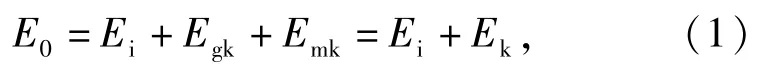
式中：E0為單位質量炸藥的化學能；Ei爆轟產物膨脹做功后自身剩余內能；Egk和Emk分別為爆轟產物動能和金屬圓筒動能，二者之和Ek為炸藥驅動金屬加速運動的有效能量，反映炸藥對金屬的驅動能力，在格尼公式中記為格尼能。格尼假設中炸藥的能量全部轉換為金屬和爆轟產物的動能，可見格尼能是驅動的有效能量的極限值，是炸藥驅動金屬的潛能。

在爆轟產物驅動金屬加速運動的系統中，物理本質為能量的不斷轉換，而能量轉換的過程取決于爆轟產物膨脹規律。本文采用爆轟產物的狀態方程來描述爆轟產物膨脹規律。目前已經有多種較為成熟的爆轟產物狀態方程形式，如γ律狀態方程、JWL、BKW、KHT及VLW狀態方程等，其中JWL狀態方程能夠比較精確地描述爆轟產物的膨脹驅動過程，應用最為廣泛。JWL狀態方程是由Lee等［9］于1965年在Jones和Wilkins工作的基礎上提出的，該方程的未知參數需要通過Kury等［10］提出的圓筒試驗及二維流體動力學程序來確定。JWL狀態方程不顯含化學反應，能精確描述爆轟產物的等熵膨脹過程，其形式為

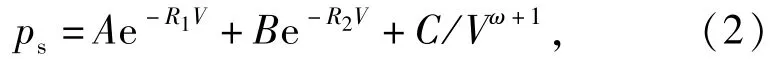
式中，ps為爆轟產物壓力；V為爆轟產物的相對比容；A、B、C、R1、R2和ω為JWL狀態方程的6個待定參數。

由熱力學關系式：

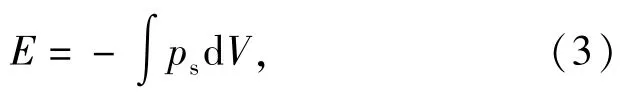
則可得到JWL狀態方程的等熵內能形式：

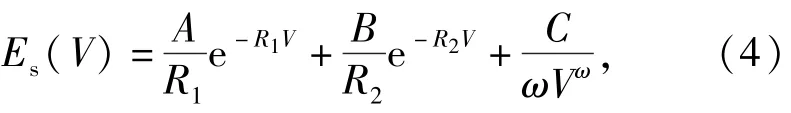
式中：Es（V）為爆轟產物的等熵內能，它是比容V的函數。炸藥瞬時定容爆轟，則V=1，此時為驅動的初態，則有

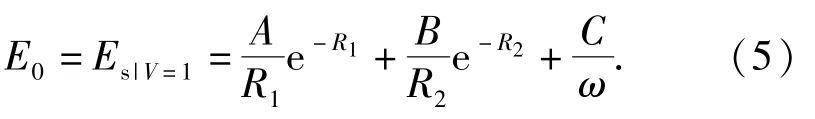
高溫高壓的爆轟產物膨脹做功驅動金屬圓筒加速運動，圓筒在膨脹過程中裂紋首先從外表面發生。當圓筒內表面也出現裂紋時圓筒完全破碎，驅動過程完成，可近似認為圓筒破裂時刻為系統能量轉換的終態。根據假設4，圓筒的破裂半徑［8］為

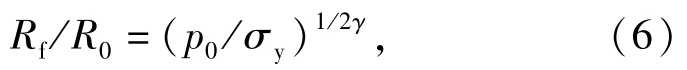
式中：Rf和R0為圓筒破裂半徑和初始半徑；p0為定容爆轟初始壓力，p0=p/2，p為理想爆轟壓力；γ為氣體多方指數；σy為金屬圓筒的屈服極限。同時Rf也為終態時刻爆轟氣體的膨脹半徑，則爆轟氣體的相對比容為

可得終態時刻爆轟氣體剩余的內能為

將（5）式和（8）式代入（1）式中，得驅動的有效能量為

將（9）式代入格尼公式即可得驅動金屬圓筒的破片初速v0為

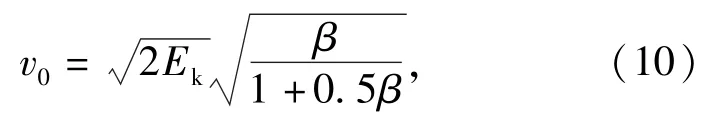
2 圓筒爆轟驅動試驗

2.1 試驗模型

本試驗參考標準圓筒試驗，選用壓裝TNT藥柱，其尺寸為φ50 mm×495 mm，炸藥參數如表1所示，圓筒參數如表2所示，其中無氧銅和6061鋁合金未進行熱處理，45#鋼先進行850℃正火，然后840℃保溫20 min，油淬。狹縫位置距離起爆端295 mm，采用GSJ高速轉鏡相機記錄圓筒壁在狹縫兩端的膨脹過程，掃描速度是1.5 mm/μs，并通過固定在圓筒兩端的電探針測定炸藥的實際爆速。試驗裝置原理圖如圖1所示，現場圖如圖2所示。

表1 試驗用炸藥參數表Tab.1 Parameters of experimental explosive

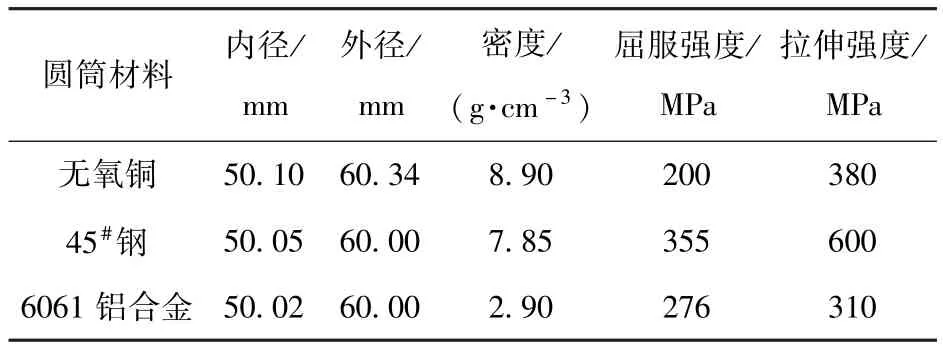
表2 試驗用圓筒參數表Tab.2 Parameters of cylinder

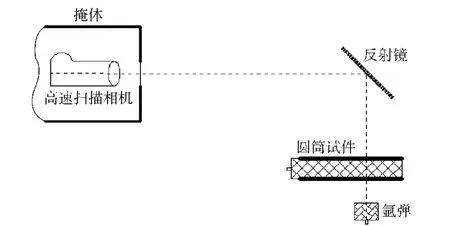
圖1 試驗原理示意圖Fig.1 Schematic diagram of cylinder test

圖2 試驗裝置現場圖Fig.2 Cylinder test site

2.2 試驗數據處理

試驗獲得的圓筒壁膨脹過程的掃描底片如圖3所示。對底片進行判讀，得到圓筒壁膨脹距離RR0與時間t曲線，如圖4所示。

試驗數據處理采用文獻［11］的處理方法，認為圓筒壁在爆炸沖擊波和氣體膨脹產物兩種力的共同作用下發生膨脹運動。沖擊波作用力使得圓筒壁在初期膨脹速度迅速增加，但持續時間較短；而氣體爆轟產物膨脹時的作用力峰值雖然偏低，但持續時間較長。圓筒壁膨脹距離R-R0與膨脹時間t有如下關系：

圖3 圓筒壁膨脹過程掃描底片Fig.3 Scanning negatives of intumescent cylinder

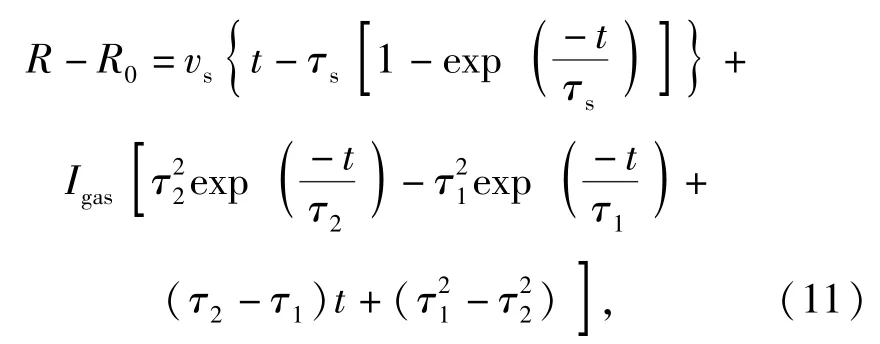
式中：R和R0分別為圓筒t時刻和初始時刻半徑；vs為沖擊波作用力使得圓筒壁達到的漸進速度；τs為其加速時間段；Igas為氣體爆轟產物作用力波動的幅度；τ1和τ2分別為爆轟產物作用力波動時上升和下降的時間常數。將（11）式對時間求導，可得到圓筒壁的膨脹速度u計算公式。

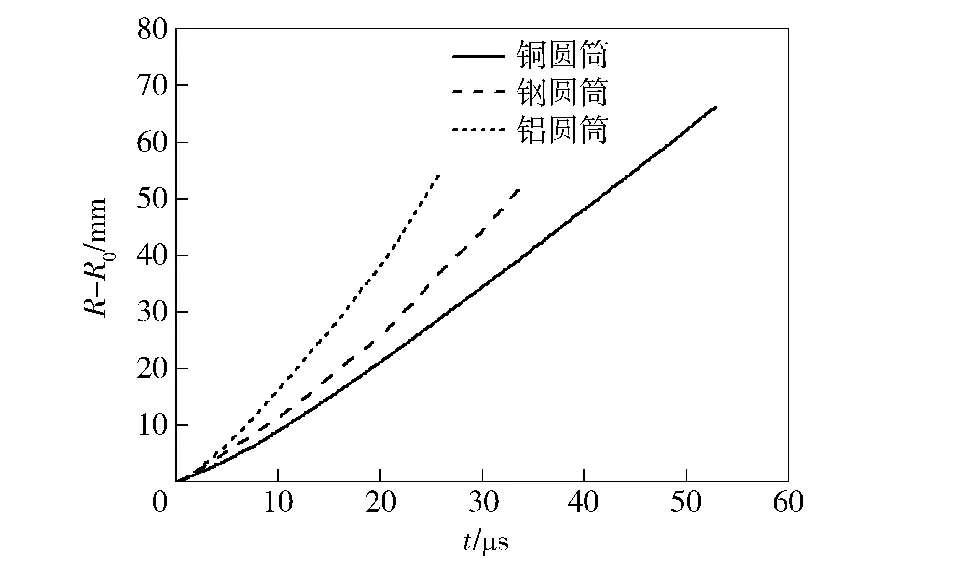
圖4 不同材料圓筒壁膨脹距離與時間曲線Fig.4 Expansion distance-time curves of different cylinders

將試驗獲得的不同材料圓筒壁膨脹距離與時間數據按（11）式進行擬合，其擬合系數見表3.將表3中擬合參數代入（12）式中，可得到圓筒壁膨脹速度隨時間變化曲線，如圖5所示。由圖5可以看出，在圓筒膨脹初期，圓筒壁在沖擊波的作用下，膨脹速度迅速增大；隨后圓筒壁在爆轟產物作用下，膨脹速度緩慢增大，直至破裂速度達到最大值。

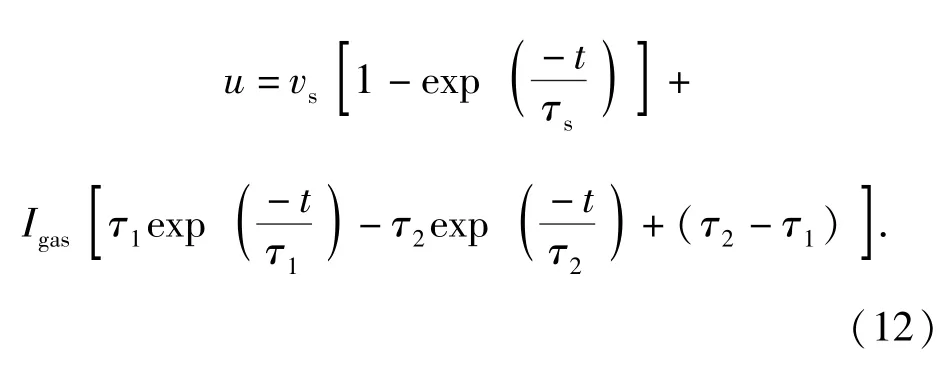
表3 不同材料圓筒壁膨脹位移曲線擬合參數Tab.3 Fitting parameters of expansion distance curves of different cylinders

3 分析討論

分析爆轟驅動金屬加速運動的能量模型可知，在炸藥-金屬驅動系統中，除炸藥的爆轟參數外，爆轟產物的膨脹過程和金屬圓筒的力學性能也是影響破片初速的因素。

3.1 圓筒力學性能的影響

在炸藥驅動金屬系統中，圓筒約束爆轟產物的膨脹過程，不同材料圓筒由于力學性能的不同，在相同的驅動能力下，其破裂半徑和破裂時爆轟產物的相對比容存在差異。由（6）式和（7）式可計算出3種不同圓筒破裂時刻的膨脹半徑和爆轟氣體的相對比容，如表4所示。從表4可看出，無氧銅的延展性最好，故其膨脹破裂時相對比容最大，45#鋼的塑性最差，膨脹破裂半徑最小。

根據模型可計算不同材料圓筒的驅動的有效能量，如表5所示。從表5可以看出，格尼公式單一的從炸藥的爆轟參數來表征驅動金屬的能力，對應同一炸藥參數，其格尼能的結果一致。但在實際工程中，由于金屬材料力學性質的不同，將出現不同的結果。本文模型考慮爆轟產物膨脹的過程，圓筒的約束影響膨脹驅動過程中的能量轉換的終態，殼體塑性越好，總能量向驅動能量轉換的比例越大，即能量利用率越高。從表5數據還可以看出，無氧銅的能量利用率最大，45#鋼能量利用率最小。

圖5 不同材料圓筒壁膨脹速度與時間曲線Fig.5 Expansion velocity-time curves of different cylinders

表4 不同圓筒膨脹的破裂半徑和相對比容Tab.4 Broken radius and specific volumes of different cylinders

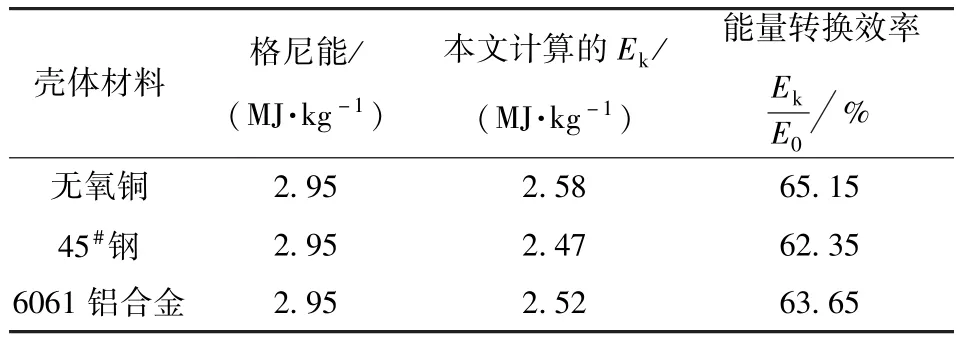
表5 不同圓筒膨脹的驅動能量Tab.5 Expansion energies of different cylinders

3.2 爆轟產物狀態方程的影響

格尼公式在計算破片初速時只考慮初始和終止狀態，并沒有考慮膨脹驅動的過程，而膨脹驅動過程決定能量轉換效率。本文模型選用JWL狀態方程來描述膨脹驅動的中間過程。圖6為3種不同材料圓筒膨脹速度試驗值和本模型計算值的對比圖。由圖5可以看出，對于理想炸藥，模型計算值與試驗值相符度較高，JWL狀態方程能很好地反映整個驅動過程。

圖6 不同材料圓筒膨脹速度與相對比容曲線Fig.6 Expansion velocity-specific volume curves of different cylinders

表6中列出試驗中圓筒壁膨脹到一些特殊位置時所對應的膨脹速度，其中圓筒壁膨脹距離分別為10.5 mm、25.0 mm和41.0 mm時，炸藥爆轟產物的相對比容分別為2、4和7，以及理論膨脹破裂的相對比容Vf.由表6可以看出，膨脹速度在驅動初期增長較快，到V大于4之后增長緩慢。從試驗數據看，在理論破裂值之后膨脹速度依然有所增大，這是由于破裂后的爆轟氣體在短時期內依然對破片有加速作用，符合物理本質規律。

通過模型計算的3種不同材料殼體的破片初速如表7所示。由表7可以看出，格尼模型所得的驅動速度高于試驗值。本模型在考慮了爆轟產物膨脹和殼體破裂機理的因素下，計算驅動初速度更接近試驗值，誤差在5%以內。

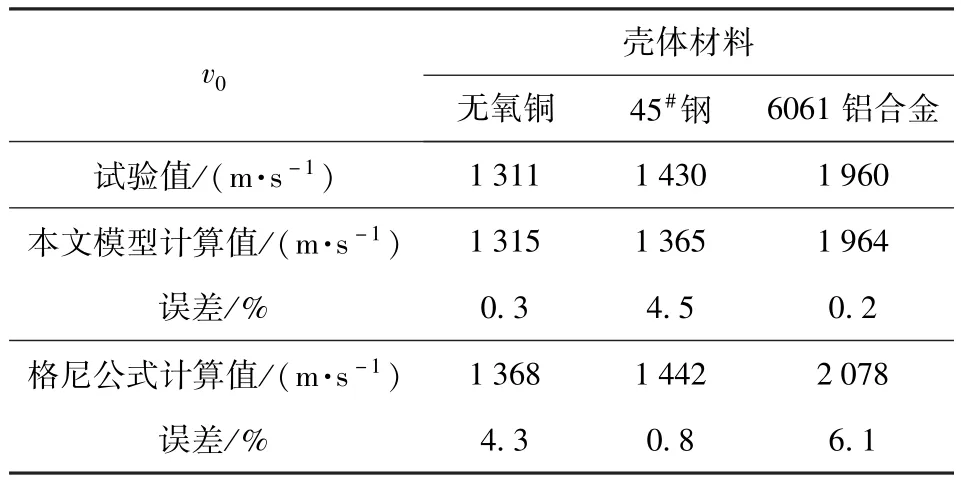
表7 不同材料圓筒破片初速Tab.7 Fragment velocities of different cylinders

4 結論

在等容爆轟假設條件下，基于JWL狀態方程和Taylor破裂判據，推導了炸藥爆轟驅動金屬圓筒的能量轉換與破片初速模型，通過TNT炸藥驅動3種不同材料圓筒試驗，分析膨脹軌跡和破片初速，得到以下結論：

1）本文建立的爆轟驅動模型綜合考慮了炸藥-金屬系統驅動的膨脹過程和力學性能因素，相比格尼公式只單一考慮炸藥爆轟參數的驅動能力，計算結果更具有針對性和適用性。

2）模型選用JWL狀態方程描述膨脹驅動的中間過程，理想炸藥的膨脹驅動速度值與試驗值符合度較好，對于非理想炸藥狀態方程的選擇有待進一步驗證。

（

）

［1］Gurney G W.The initial velocities of fragments from bombs，shells and grenades［R］.Aberdeen，Maryland，US：Ballistics Research Laboratories，1943.

［2］Danel J F，Kazandjian L.A few remarks about the Gurney energy of condensed explosives［J］.Propellants，Explosives，Pyrotechnics，2004，29（5）：314-316.

［3］Koch A，Arnold N，Estermann M.A simple relation between the detonation velocity of an explosive and its Gurney energy［J］. Propellants，Explosives，Pyrotechnics.2007，27（6）：365-368.

［4］Keshavarz M H.New method for prediction of the Gurney energy of high explosives［J］.Propellants，Explosives，Pyrotechnics，2008，33（4）：316-320.

［5］Kennedy J E，Schwarz A C.Detonation transfer by flyer plate impact［C］∥8th Symposium on Explosives and Pyrotechnics.Philadelphia，Pennsylvania，US：Franklin Institute，1974.

［6］Taylor G I.Fragmentation of tubular bombs：science papers of Sir G I Taylor［M］.London：Cambridge University Press，1963：387-390.

［7］譚多望，孫承緯，王彥平.炸藥爆轟產物驅動不可壓縮剛粘塑性柱殼的運動［J］.爆炸與沖擊，2000，20（4）：348-351. TAN Duo-wang，SUN Cheng-wei，WANG Yan-ping.The motion of an incompressible rigid-viscos-plastic cylinder driven by detonation products of explosives［J］.Explosion and Shock Waves，2000，20（4）：348-351.（in Chinese）

［8］劉益儒，段卓平，歐卓成，等.多元混合炸藥爆轟驅動圓筒膨脹規律的理論確定方法［J］.高壓物理學報，2014，28（4）：435-441. LIU Yi-ru，DUAN Zhuo-ping，OU Zhuo-cheng，et al.Theoretical approach of determining expansion law of cylinder under the detonation driving of multi-component explosive［J］.Chinese Journal of High Pressure Physics，2014，28（4）：435-441.（in Chinese）［9］Lee E L，Hornig H C，Kury J W.Adiabatic expansion of high explosive detonation products，UCRL-50422［R］.San Francisco：U-niversity of California，1968.

［10］Kury J W，Hornig H C，Lee E L，et al.Metal acceleration by chemical explosives［C］∥4th International Symposium on Detonation. White Oak，MD：US Naval Ordnance Laboratory，1965：3-13.

［11］Lindsay C M，Butler G C，Rumchik C G.Increasing the utility of the copper cylinder expansion test［J］.Propellants，Explosives，Pyrotechnics，2010，35（5）：433-439.

The Energy Conversion and Fragment Initial Velocity Model of Metal Cylinder Driven by Detonation

WANG Xin-ying，WANG Shu-shan，XU Yu-xin，HU Sai
（School of Mechatronical Engineering，Beijing Institute of Technology，Beijing 100081，China）

Based on the JWL equation of state of detonation products and Taylor fracture criteria，a model considered the expansion details about energy conversion and fragment initial velocity is derived from conversation of energy.The cylinder tests of three materials，including copper，45#steel and 6061 aluminum alloy，driven by TNT explosive are made，and the inflation track and velocity are analyzed.The experimental results show that，by comparing with Gurney formula which is considered only to express the driving ability of the explosion parameter，the proposed model considers the driving factors，inflation process and mechanics function of meta.The result is of pertinence and applicability.

ordnance science and technology；detonation driven；equation of state；energy conversion；fragment initial velocity

TJ012.4

A

1000-1093（2015）08-1417-06

10.3969/j.issn.1000-1093.2015.08.007

2014-10-23

國家“863”計劃項目（00404020304）

王新穎（1980—），女，博士研究生。E-mail：wxy801003@163.com；王樹山（1965—），男，教授，博士生導師。E-mail：wangshushan@bit.edu.cn