變截面異形連續梁橋多軟件靜力計算比較

張四國 閆 旭

(天津市市政工程設計研究院，天津 300051)

0 引言

橋梁結構受力分析驗算模型根據研究重點的不同，可以有單梁模型、梁格模型和三維實體有限元模型，不同模型都可以從不同的角度顯示橋梁的受力特性，其中三維實體模型對結構受力的表達最清晰，但無法直接得到規范中驗算的結果，單梁模型無法得到結構在橫向尺寸上的應力分布，但可根據規范直接驗算承載力，梁格模型是把原結構離散為縱向與橫向剛度近似地與該處縱、橫梁所代表局部范圍內板的剛度相同的等效梁格代表，是對原結構的一種人為離散，其物理意義是:假定把分散在橋梁上部結構的每一部分的彎曲與扭轉剛度集中到與其相鄰的梁格內，確保等效后的梁格與實際橋梁在相同的荷載作用下恒具有相同的撓度，且任一梁格內彎矩、剪力和扭矩應等于該梁格所代表的實際結構部分的內力，本質上為梁模型，縱橫向梁格分別顯示橋梁縱橫向受力特性，建模相對簡單，驗算方法明確［1］。本文將分別對同一結構的不同模型進行建模和比較，對比出不同方法的優缺點。

1 工程背景

如圖1 所示為設計橋梁的平面外形示意圖，橋梁采用變截面T 構結構，跨徑布置為3×40 m +90 m +3×40 m，全長330 m，中跨90 m 中間設置20 m 跨徑掛孔以釋放溫度力，混凝土強度等級C50，掛孔采用牌號為Q345 鋼材。結構驗算時考慮結構自重、預應力和溫度荷載，升溫按20 ℃考慮，降溫按－20 ℃考慮，不考慮梯度溫度效應和車輛活載效應。

圖1 橋梁外形平面圖

2 驗算原則

如圖2 所示分別為在橋梁博士中建立的單梁模型、在Midas中建立的梁格模型和在ANSYS 中建立的實體有限元模型，梁模型中點1～點10 為應力驗算點。在ANSYS 中，采用Solid45 實體單元模擬主橋混凝土，采用Link10 單元模擬預應力鋼束［2，3］，實體單元和桿單元之間通過節點耦合傳力，全橋共21 萬個節點，71 萬個單元。

對模型進行靜力分析后，提取最不利關鍵截面和節點的應力和撓度，與規范［4，5］中的容許值進行比較，判斷橋梁是否滿足規范要求。規范中規定預應力混凝土受彎構件按荷載短期效應組合并乘以撓度長期增長系數所得的長期撓度值，在消除結構自重產生的長期撓度后，梁式橋主梁的最大撓度處不應超過計算跨徑的1/600，主梁懸臂端不應超過懸臂長度的1/300。

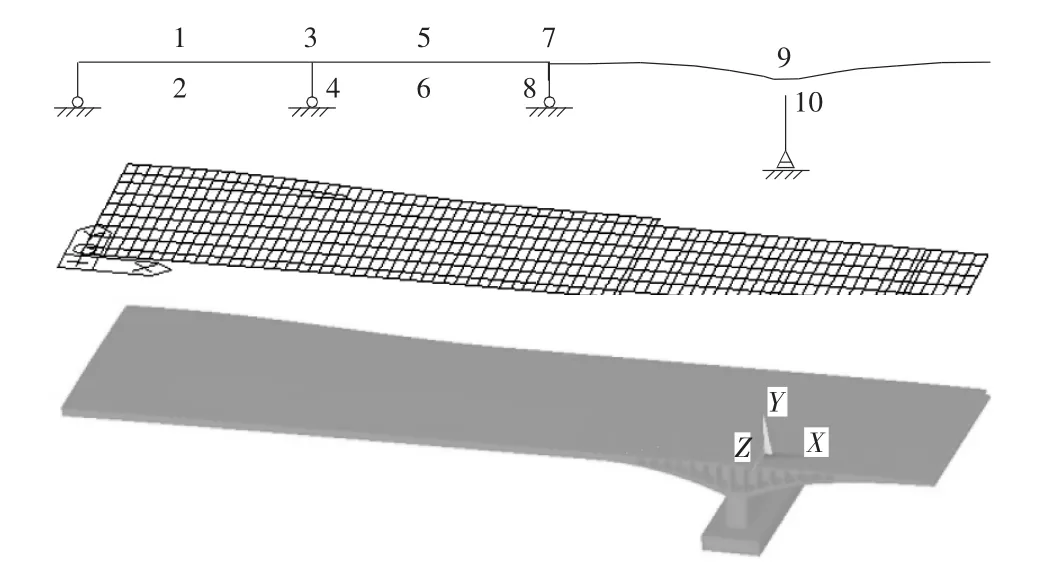
圖2 單梁模型、梁格模型和實體模型

3 單一工況計算結果

3.1 自重作用下計算結果

如表1 所示為自重作用下不同模型的支座反力匯總，表1 中顯示，不同模型下的支座反力相差不大，4 號墩為T 構處，該處承擔了橋梁60%以上的重量;如表2 所示為自重作用下不同模型的位移匯總，下撓為負值，表中顯示不同模型求得的各跨跨中位移相差不大，但主梁懸臂端的豎向撓度相差很大;如圖3 所示為不同模型下應力驗算點的正應力，拉應力為正值，可見不同模型求得的關鍵點的正應力相差不大，除4 號點(2 號墩支座下緣)應力差別相對明顯外，三者吻合較好。

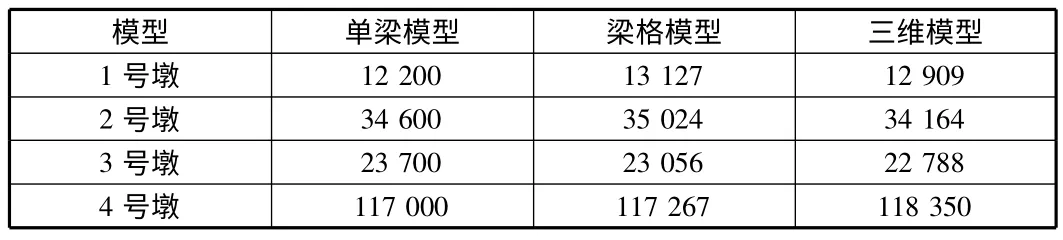
表1 自重下不同模型的支座反力 kN

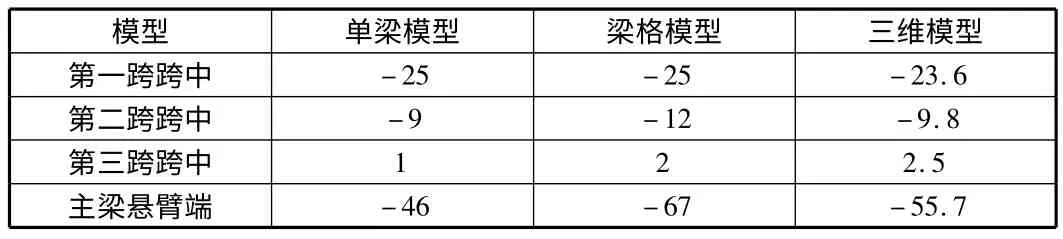
表2 自重下不同模型參考點的位移 mm

3.2 預應力荷載下的計算結果

如表3 所示為預應力作用下不同模型的支座反力匯總，表中顯示，單梁模型和梁格模型下各墩處反力相差不大，但實體模型2 號～4 號墩反力與兩者差異很大，但反力方向相同;如表4 所示為預應力作用下不同模型的位移匯總，下撓為負值，表中顯示三種模型都能精確表示跨中和懸臂端的位移變化規律;如圖4 所示為不同模型下應力驗算點的正應力，拉應力為正值，可見不同模型求得的關鍵點的正應力相差不大，在預應力作用下，除支座下緣混凝土會出現較小的拉應力外，全截面均受壓。

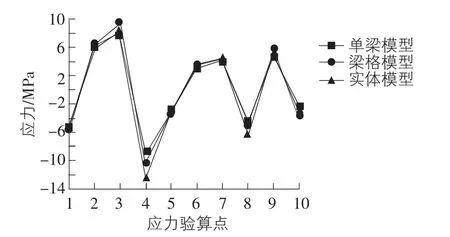
圖3 自重下不同模型驗算點的正應力

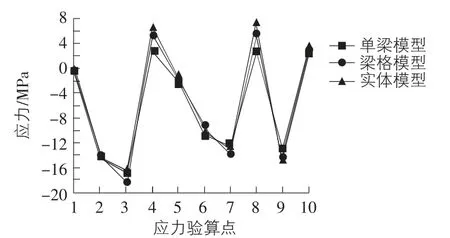
圖4 預應力下不同模型驗算點的正應力

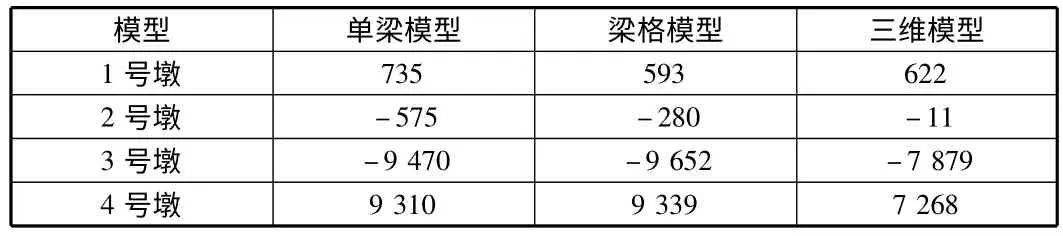
表3 預應力下不同模型的支座反力 kN

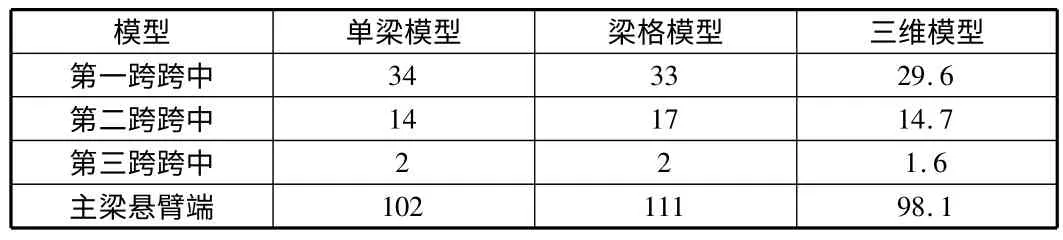
表4 預應力下不同模型參考點的位移 mm

3.3 升溫(降溫)20 ℃下的計算結果

如表5 所示為升溫作用下不同模型的支座反力匯總，表中顯示，單梁模型和梁格模型下各墩處反力相差不大，但實體模型3 號～4 號墩反力與兩者差異很大，但反力方向相同;如表6 所示為升溫作用下不同模型的位移匯總，下撓為負值，表中顯示梁模型的計算結果相差不大，實體模型與兩者差異很大;如圖5 所示為不同模型下應力驗算點的正應力，拉應力為正值，可見不同模型求得的關鍵點的正應力相差不大，僅在3 號墩支座下緣處，實體模型求得的壓應力偏大。降溫作用下，表中和圖中數字為反號。

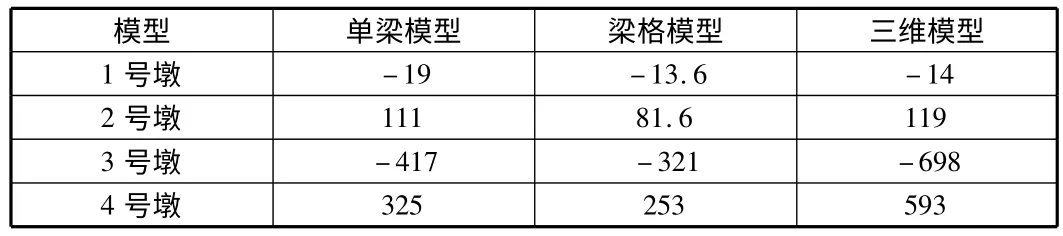
表5 升溫下不同模型的支座反力 kN

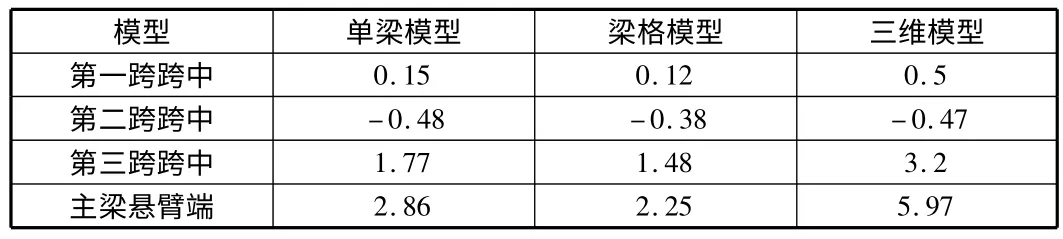
表6 升溫下不同模型參考點的位移 mm

4 不利工況組合計算結果

4.1 組合撓度驗算

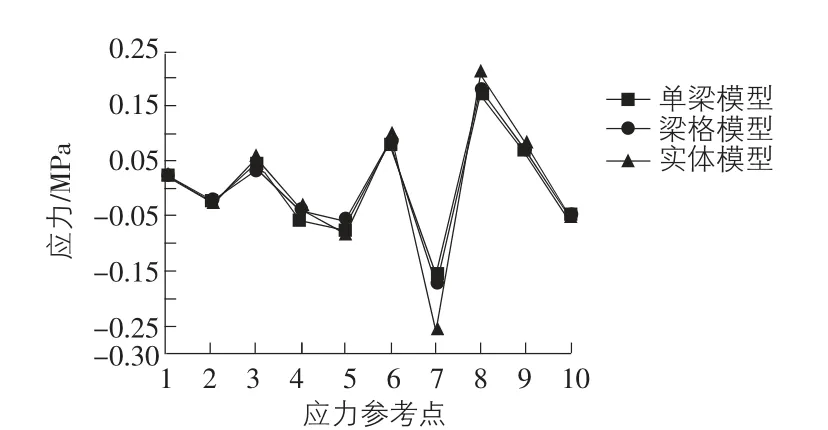
圖5 升溫下不同模型驗算點的正應力

如表7 所示為不同工況短期組合作用下考慮了長期效應(ηθ=1.425)不同模型的位移匯總，下撓為負值。可見，梁格模型和實體模型的計算結果更為相近，而橋梁博士中單梁模型結果相對來說誤差很大，尤其是主梁懸臂端的位移與梁格模型的誤差為27%，因此撓度驗算推薦梁格模型或實體模型。

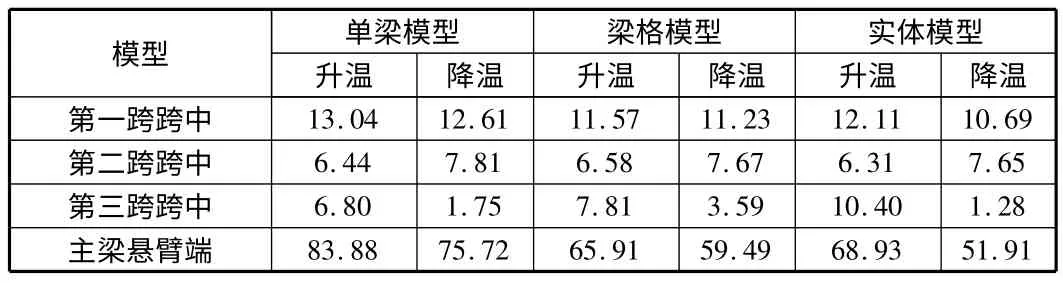
表7 不同工況下不同模型參考點的位移 mm

表7 中顯示，升溫作用下，主梁最大撓度發生在第一跨跨中，大小為12.11 mm，不超過計算跨徑的1/600;主梁懸臂端的最大撓度為68.93 mm，不超過懸臂長度的1/300，撓度驗算符合規范要求。

4.2 組合應力驗算

如表8 所示為不同工況短期和長期組合作用下應力驗算點的正應力，拉應力為正值，可見，梁格模型和單梁模型的計算結果更為相近，且全橋不出現拉應力，而ANSYS 中實體模型在8 號點位和10 號點位處出現了拉應力，結果相對來說誤差很大，因此應力驗算推薦梁格模型或單梁模型，以避免局部應力失真。

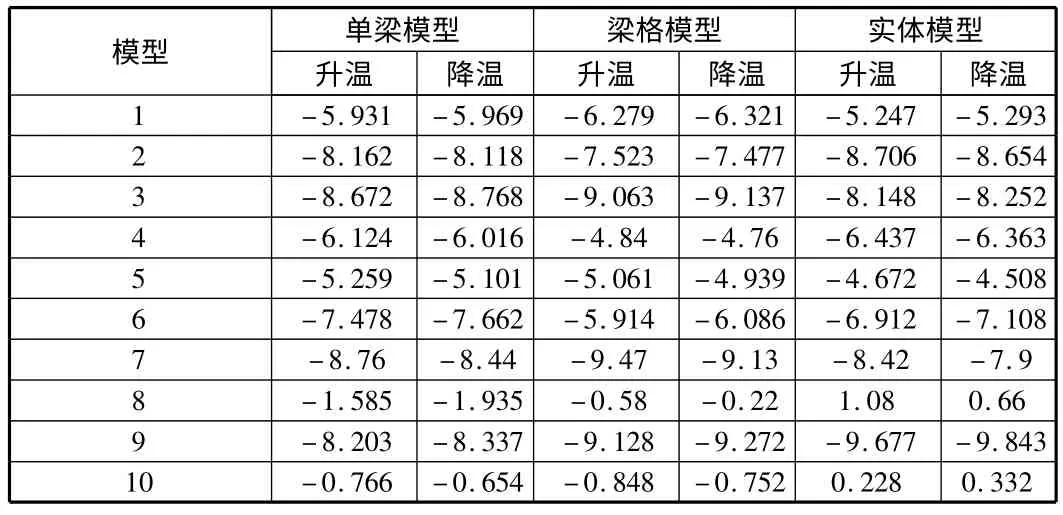
表8 不同工況下不同模型驗算點的正應力 MPa

與規范中抗裂要求比較，全橋應力符合規范中A 類構件的應力要求，結構安全可靠。

5 結語

本文分別利用橋梁博士、Midas 和ANSYS 軟件建立了某變截面異形連續梁橋的單梁模型、梁格模型和三維實體有限元模型，在不同的荷載工況下進行了靜力計算，結果表明:該橋的縱向抗裂性能良好，不會出現橫向裂縫，符合規范中對A 類預應力構件的抗裂要求;撓度驗算符合規范要求;單梁模型在求解撓度時會產生誤差，實體模型在求解應力時會出現失真，梁格模型可以彌補單梁模型和實體模型的不足，在允許的情況下，建議結構受力分析時建立梁格模型進行計算。

［1］戴公連，李建德.橋梁結構空間分析設計方法與應用［M］.北京:人民交通出版社，2001.

［2］張立明.Algor、Ansys 在橋梁工程中的應用方法與實例［M］.北京:人民交通出版社，2009.

［3］郝文化.Ansys 土木工程應用實例［M］.北京:中國水利水電出版社，2005.

［4］JTG/D 62—2004，公路鋼筋混凝土及預應力混凝土橋涵設計規范［S］.

［5］JTG/D 60—2004，公路橋涵設計通用規范［S］.