例析教學中的質(zhì)疑引導

江蘇如東縣雙甸鎮(zhèn)雙甸小學（226404） 袁 旭

例析教學中的質(zhì)疑引導

江蘇如東縣雙甸鎮(zhèn)雙甸小學（226404） 袁 旭

小孩子從小就喜歡問“為什么”。因此，課堂教學中，教師要精心設(shè)計教學活動，調(diào)動學生的學習積極性，鼓勵學生質(zhì)疑問難，讓學生學會獨立思考，使學生在數(shù)學上獲得更好的發(fā)展。

數(shù)學教學 設(shè)計教學 質(zhì)疑 獨立思考 發(fā)展

我們都知道，自會說話起，小孩子就喜歡問“為什么”。課堂教學中，如果教師方法得當，讓學生保持這種好奇心，不去打擊、敷衍，而是積極去引導，就能使學生學會質(zhì)疑、獨立思考，進而解決問題。

于本質(zhì)處質(zhì)疑：垂直線段就是最近的路線嗎？

學生獲得知識，必須建立在自己思考的基礎(chǔ)上，只有親身經(jīng)歷探究、體驗的過程，才能在數(shù)學思考、問題解決和情感態(tài)度等方面得到發(fā)展。

例如，教學“平行和相交”這一內(nèi)容時，在學生學習點到直線的距離后，我精心設(shè)計這樣一道題（如圖1）：“小明站在小河邊（A點），他想到河的對岸去。他走怎樣的路線過河是最近的？”多數(shù)學生會這樣想“最近的路線不就是垂直線段嗎？這簡單”，然后拿起筆和尺，一會兒就畫好了（如圖2）。但生1說：“這樣畫是錯的。”有的學生納悶了：“怎么會錯呢？難道是垂直線段畫得不夠標準？”于是，一些學生又拿起三角尺檢查了一下，發(fā)現(xiàn)沒錯，不禁質(zhì)疑：“難道垂直線段不是最短的？到底怎么回事呢？”在學生百思不得其解時，我請生1上臺說說自己的想法。生1：“一開始我也畫錯了，但總覺得不對勁，所以我又打開書（如圖3）仔細看了看。當時心想，這道題也是說說直線外一點到這條直線的距離，跟書上的是一樣的，只不過A點在直線下方而已。想到這兒，我猛然發(fā)現(xiàn)問題所在，原來這道題目比較狡猾！多了一條直線，就把我們搞得暈頭轉(zhuǎn)向了。其實，我們應該這樣想：哪里是直線外一點？哪里是這一點要到的直線？這道題應是從這個點到這條直線畫垂直線段，而不是從這條直線到這個點畫垂直線段！也就是說，這條垂直線段應該與河的對岸互相垂直（如圖4），而不是和自己所在的河岸互相垂直！”

圖1

圖2

圖3

最后，生1總結(jié)說：“總之，最短路線還是垂直線段，但不是隨便畫條垂直線段就是最短的，而是要看與誰互相垂直！這讓我想起了一個成語——南轅北轍，說明目的地是很重要的，一開始我做錯了，就是把目的地給弄錯了。現(xiàn)在我終于弄清了癥結(jié)所在，同時也懂得了一個道理，那就是要透過現(xiàn)象看本質(zhì)，做數(shù)學題也是如此。”其他學生都為他精彩的發(fā)言而鼓掌。

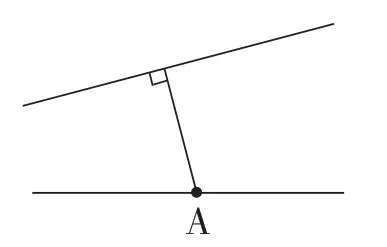
圖4

于創(chuàng)新處質(zhì)疑：是三種擺法，還是無數(shù)種？

創(chuàng)新意識的培養(yǎng)是現(xiàn)代數(shù)學教育的基本任務，而獨立思考、學會思考是創(chuàng)新的核心。因此，課堂教學中，教師應努力提高學生獨立思考的能力，培養(yǎng)他們的創(chuàng)新意識。

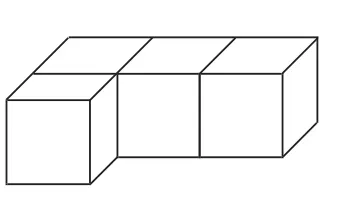
由于小學生的思維以形象思維為主，所以在教學“觀察物體”這一內(nèi)容時，我調(diào)動學生的學習積極性，讓學生在實際操作中學習。在課上，我設(shè)計了這樣一道題目（如右圖）：“再添一個同樣大的正方體，使得從正面看到的樣子不變，有幾種擺法？”學生用小正方體在課桌上試著擺了擺，最后統(tǒng)一意見有三種擺法，即分別放在三個正方體的后面，這樣添加的一個正方體從正面看就被擋住了，不影響看到的形狀了。如下圖：

這時，一學生忽然舉手說：“老師，這道題有無數(shù)種擺法！”“什么？”“哇！”其他學生都發(fā)出驚訝的聲音。有的學生則質(zhì)疑：“怎么可能呢？”我覺得他可能有自己獨特的想法，就鼓勵他說：“你是怎么擺的？能到前面擺給大家看嗎？”他信心十足地走上前來，邊擺邊說：“一開始我也得出三種擺法，但我一直在想還有沒有其他的擺法。于是，我蹲下來從正面看，邊看邊移動添加的那一個正方體，卻發(fā)現(xiàn)沒有和原來的正方體對齊時，從正面看仍然是原來的樣子（如右圖）。這時，我猛然想到：從正面看樣子不變，只要把這一個正方體藏在后面就好了，不一定要和前面的對齊！也就是說，添加的這個正方體在后面隨便移動都行，從正面看還是原來的形狀，所以有無數(shù)種擺法。”我及時肯定了他的想法，并且表揚了他，全班學生向他投去敬佩的目光。他課后說：“看來，做數(shù)學題不能形成思維定式，有些題目還是要從多方面加以嘗試！”……

于平常處質(zhì)疑：答案只有兩種嗎？

在教學“找規(guī)律”這部分內(nèi)容時，有些學生覺得自己學得很好，可是萬萬沒有想到，課本上“想想做做”中一道看似很平常的題目，卻讓這些學生的想法改變了，因為交流時出現(xiàn)了這些學生沒有想到的答案。

題目：“一條走廊長24米，每隔3米放一盆花，要放多少盆花？走廊的兩端放花和不放花一樣嗎？”當時課上交流時，多數(shù)學生認為：把走廊平均分成3米長的小段，一共有24÷3=8（段），如果兩端放花，那么花的盆數(shù)就比段數(shù)多1，即8+1=9（盆）；如果不放花，那情況就不一樣了，花的盆數(shù)就比段數(shù)少1，即8-1=7（盆）。有的學生還在草稿紙上畫了圖（如下），并進行了檢查。

做完之后，這些學生以為自己做得既快又好，可是在全班交流時，一個學生卻說出了讓他們意想不到的答案：“兩端不放花也可能是8盆！”班上的多數(shù)學生都認為這個答案是錯的，可是這個學生接下來的話卻讓全班學生都傻了眼：“花不一定要放在每一小段的分界處！走廊一共有8小段，如果兩端不放花，那么也可以每一小段放一盆花，8小段就放8盆花。”一石激起千層浪，學生恍然大悟：原來兩端不放花時，還可以把花放在每一小段的任意位置，只要位置相同（每一小段的端點處除外，比如每一小段的中點處，當然也不限于中點），這樣花的盆數(shù)就和段數(shù)相同了。如在每小段中點處放花盆（如下圖），此時花盆數(shù)就是24÷3=8（盆）。也就是說，本題答案應該有3個，即兩端都放花共9盆，兩端不放花可能是8盆，也可能是7盆，這樣做才是最全面的。這個學生的精彩發(fā)言，讓其他學生都得到一個經(jīng)驗：像這樣答案有多個的題目，在我們今后的學習過程中肯定還會遇到，這就要求我們要認真審題、仔細推敲，不能自以為是、以偏概全。

綜上所述，我們一線教師在平時的教學中，應著眼于學生的思維“最近發(fā)展區(qū)”，精心設(shè)計教學活動，調(diào)動學生的學習積極性，多鼓勵學生質(zhì)疑，讓學生學會獨立思考，使學生在數(shù)學上獲得更好的發(fā)展。

（責編 藍 天）

G623.5

A

1007-9068（2015）08-044