長江口洪水期潮波變形數值模擬研究

路川藤，羅小峰，韓玉芳

(南京水利科學研究院 水文水資源與水利工程科學國家重點實驗室，江蘇 南京 210029)

研究潮波變形的方法主要有三種。一為現場水文觀測研究，這是研究河口潮波變形的最直接手段，結論可信實用，但成本較高。如Kosuth 等［2］指出特定徑流與潮汐情況下，亞馬遜河口可同時出現3 個波峰。二為半經驗解析模型，是估算潮波傳播比較實用的工具，但計算結果誤差較大。該方法基于的理論方程為圣維南方程以及潮波能量輸運方程，通過不同的離散格式，離散理論方程，在概化地形的基礎上，考慮底摩擦［3］、河口邊界形狀［4-6］、徑流對潮差、潮波能量沿程變化的影響。三為數學模型研究，是目前研究潮波傳播的主要手段。數學模型采用不同方法［7-8］離散N-S 方程，在計算機上實現程序運算，計算成本低，可操作性強，可視化好，但數學模型計算結果的優劣取決于計算格式、網格的疏密［9］及計算參數［10］等眾多因素。

在近海或者河口地區，水深相對較淺，潮波向前傳播過程中，高潮位潮波傳播速度大于低潮位，即潮波傳播過程中，潮波變形會逐漸加劇。然據長江口2005 ～2010年實測水文資料(圖1 所示)分析知，洪水期，潮波上溯過程中，潮波變形具有先加劇后趨緩的特點，枯水期這一現象不明顯，這有別于一般的河口潮波傳播認識。為深入認識洪水期長江口潮波變形特點，建立大通至外海的長江口整體數學模型，分析長江口洪水期潮波變形特征。

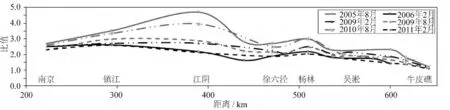
圖1 長江口潮波變形沿程變化Fig.1 The tidal wave deformation in the Yangtze estuary

1 控制方程

1.1 控制方程及離散

水流運動方程向量形式:

1.2 方程求解

采用三角形網格對計算區域進行離散，并將單一的網格單元作為控制單元，水深布置在網格頂點，其他物理變量配置在每個單元的中心，如圖2 所示。

將第i 號控制元記為Ωi，在Ωi上對向量式的基本方程組(1)進行積分，并利用Green 公式將面積分化為線積分，得

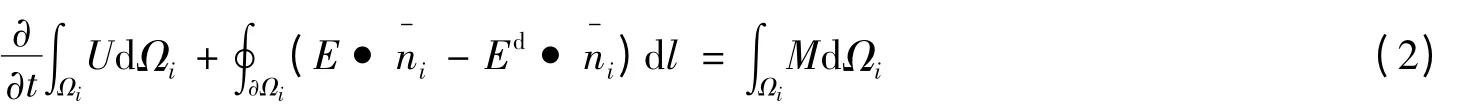
方程(2)求解主要分三部分，一為對流項求解;二為紊動項求解;三為底坡項處理。對流項數值通量可采用Roe 格式的近似Riemann 解，紊動項采用單元交界面的平均值計算通過該界面紊動粘性項的數值通量，有限體積法底坡項若不加任何處理，則會造成靜水的偽流動現象，如圖3 所示。

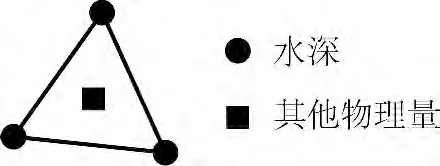
圖2 物理量布置示意Fig.2 The arrangement of physical quantities

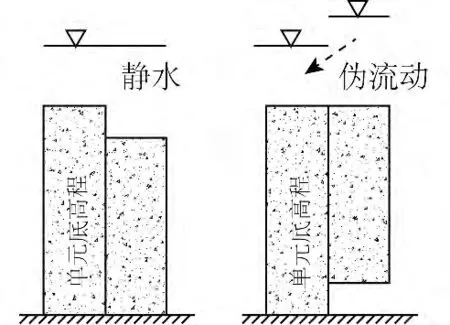
圖3 有限體積法偽流動現象Fig.3 The phenomenon of false flow in FVM

為避免水流偽流動現象，記某個控制體三個

頂點坐標為xi，yi，zi(i =1，2，3)，三個頂點按逆時針方向排序，由這三個頂點確定的平面方程為:

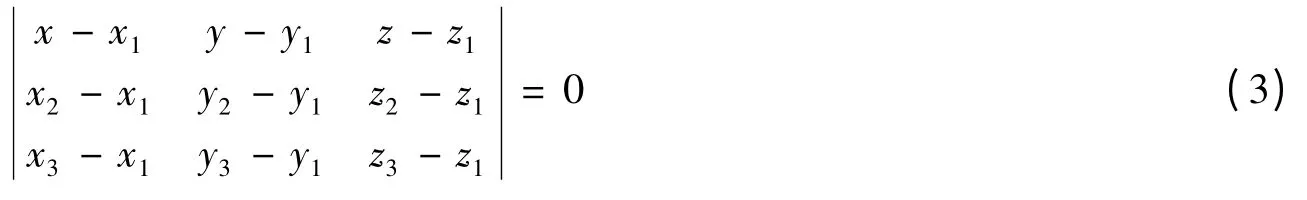
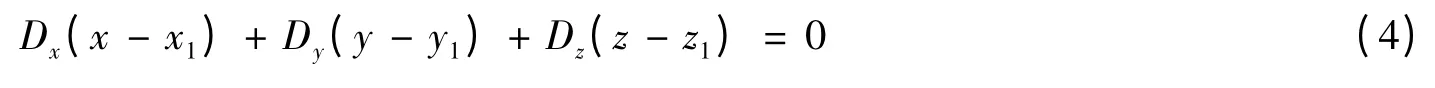
當Dz≠0 時，式(4)可寫為:

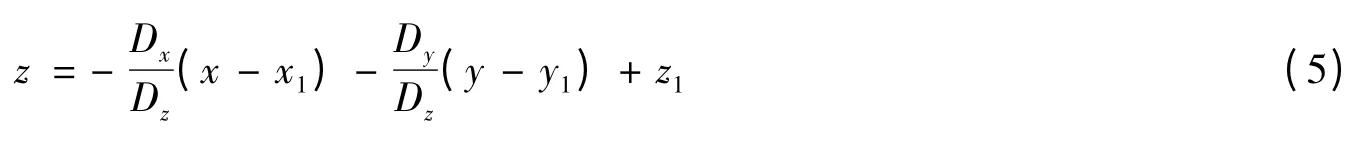
1.3 邊界條件

1.3.1 水位開邊界

開邊界又分為急流開邊界和緩流開邊界，因這里所建模型為緩流模型，故只給出緩流開邊界的處理方法。Roe 利用間斷左右的物理量UR、UL構造常數矩陣代替非線性雅可比矩陣A(Un)，并提出，當UR，UL→Un，即:

式中:cL和cR表示單元左右靜水波傳播速度。

則:

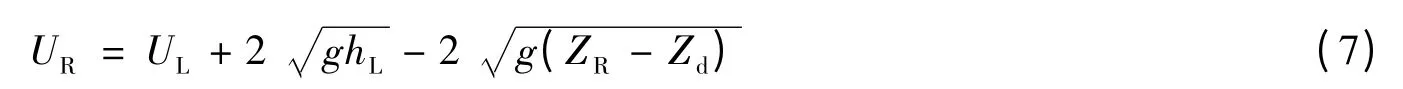
式中:Zd為邊界上通量積分點處的底高程。

1.3.2 閉邊界

采用鏡像法［11］處理。在閉邊界外側虛擬一個單元，邊界上兩側的法向流速相反，切向流速相同，即DR= DL，un，R= － un，L，uτ，R= － uτ，L，un、uτ表示單元法向和切向流速。

1.3.3 動邊界

動邊界是數學模型的難點，動邊界的處理精確與否直接影響模型計算的質量。文中動邊界技術采用干濕法，當單元水深小于hmin(動邊界水深設定值)時，認為該單元為干單元，不參與數值計算，當水深大于hmin時，該單元重新參與數值計算。

2 數學模型

2.1 模型范圍

長江潮區界位于安徽大通，大通以上水域水位基本不受潮波影響，作為模型的上邊界;長江口外－50 m等深線處受徑流影響可忽略不計，作為模型外邊界，模型總長700 多公里。模型北至江蘇呂四港南側，南至金山嘴，如圖4 所示。模型網格總數114 489 個，最小邊長128 m，時間步長4 s，紊動粘性系數取常數0.1，動邊界水深0.02 m。

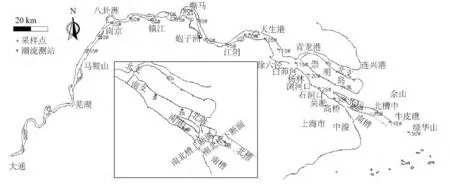
圖4 數學模型范圍Fig.4 The range of mathematical model

2.2 模型驗證

徐六涇以上地形選用2003年長江下游地形測量數據，徐六涇至綠華山地形數據選用2005年8月長江口實測地形數據，外海地形選用大范圍海圖地形數據。模型計算時間為2005年8月18日～2005年8月25日，上游邊界采用大通實時流量控制，外海潮位邊界由東中國海模型提供，驗證點位置如圖4 所示。由表1及圖5 ～6 知，各站高、低潮位值偏差大都均在10 cm 之內，個別點高低潮位值偏差超過10 cm，高低潮位相位偏差在30 分鐘內。CS6 點位于航道邊緣，流速偏差較大，因網格較粗，模型地形與實際地形有偏差，其他各點偏差基本都在10%之內，驗證良好，滿足規程要求。

表2 為各汊道分流比情況驗證，長江口北支日益萎縮，至2001年時，其落潮分流比僅占1% ～4%，南支分流比96% ～99%［12］，南北港及南北槽分流比選用2006年8月大潮實測資料驗證，本數學模型計算分流比值與實測值基本吻合。驗證說明本數學模型具有復演長江口潮波傳播的能力。

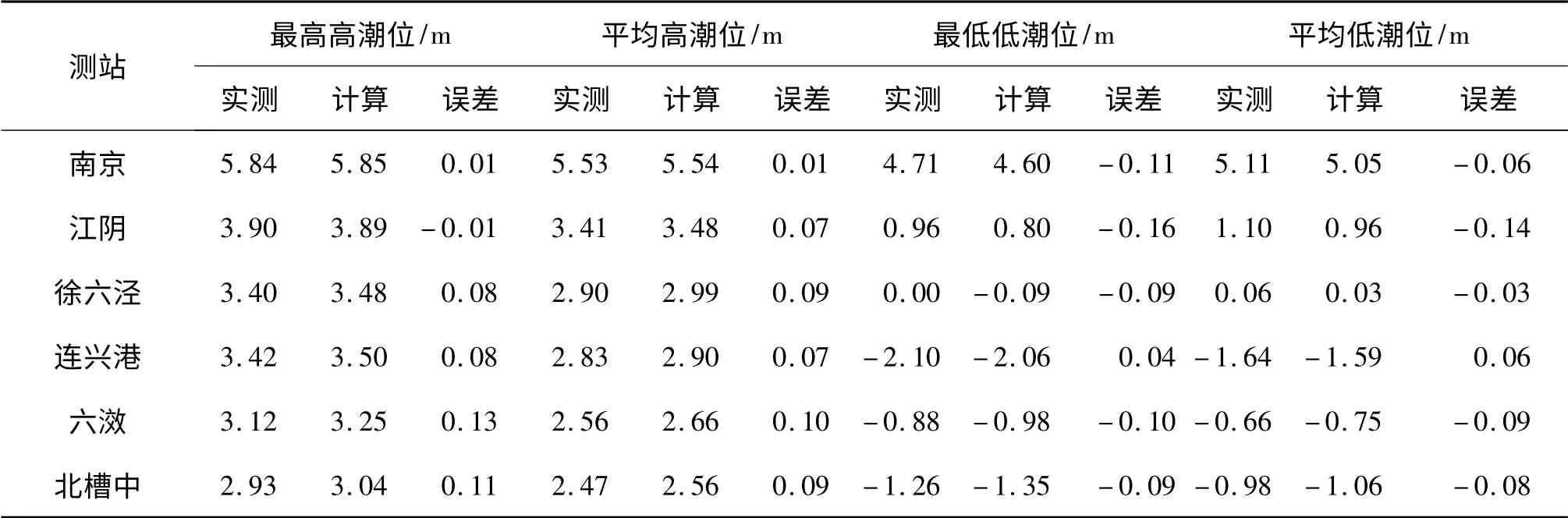
表1 潮位誤差分析Tab.1 Tidal level error analysis

表2 落潮分流比驗證Tab.2 Ebb flow ratio verification

圖5 模型潮位驗證Fig.5 The tidal level verification

圖6 模型流速驗證Fig.6 The tidal current verification

3 潮波變形影響因素分析

影響河口潮波變形的因素主要有河床底摩擦、河口邊界形狀、徑流、水深及邊灘反射等。河床底摩擦及徑流削弱潮波能量，而河口邊界形狀收縮與邊灘反射使潮波能量增強。對于某一特定河口，邊界形狀、淺灘、水深等因素短時間內相對穩定，不會發生大的格局變化，其對潮波傳播的影響亦相對穩定。

河床底摩擦在數學模型上體現為糙率，糙率是表征河床底部和岸壁影響水流阻力的綜合因素系數，與河床底質構成及水深密切相關。徑流對潮波傳播的影響反映在徑流量的大小對潮波傳播阻力影響不同。因此，年際內對潮波變形影響較大的因素為河床底摩擦與徑流。下文基于數學模型，研究河床底摩擦與徑流對潮波變形的影響。

3.1 計算條件

3.1.1 糙率

本數學模型空間尺度大，自大通至外海總長約700 km，上下游糙率取值差別大。表3 列舉了前人在長江口數學模型中糙率的取值，由表知，大通附近最大糙率取值0.032，最小0.018，口外海濱段取值約為0.012。

表3 長江感潮河段糙率選取Tab.3 Roughness selection in the Yangtze estuary

文中數學模型糙率采用附加糙率方法，即:n = n0+n＇/h，基本糙率n0自大通至外海線性插值，附加糙率n＇計算過程中固定不變，基本糙率分四種工況計算討論，見表4 所示。

表4 數學模型中大通至外海4 種基本糙率n0的取值Tab.4 The selection of basic roughness n0 from Datong to seas in mathematic model

3.1.2 徑流

模型上邊界位于長江口潮區界安徽大通，大通流量即為徑流量。據大通站實測資料分析［21］，大通站多年平均流量為28 518 m3/s，多年最小月平均流量10 400 m3/s，多年最大月平均流量48 600 m3/s，最大月平均洪峰流量84 000 m3/s。為充分分析徑流對潮波傳播的影響，分別取10 000、30 000、60 000和90 000 m3/s四種流量代表枯水流量、年平均流量、洪水流量和特大洪水流量。

3.2 潮波變形對糙率的響應

謝才公式:

式中:v 為流速，R 為水力半徑，J 為水面比降。

由上式可知，糙率的變化直接影響流速的大小。潮汐河口中，潮量由流速和水位共同反應，當潮量不變時，流速的變化必然影響潮位。由圖7 知，隨著糙率的增大，河口平均水位逐漸升高，越往上游，水位升高幅度越大，南京站最大糙率與最小糙率水位差接近0.6 m，換言之，糙率的增大可增大河口平均水面比降(如表5 所示)。徐六涇以下水域受潮汐影響大，且水面開闊，糙率對水位影響相對較小。

圖8 為潮波變形對糙率變化的響應。徐六涇站以下水域，糙率的變化對潮波變形影響相對較小。徐六涇以上水域，隨著糙率的增大，漲落潮歷時比值逐漸增大，潮波變形加劇。自下游至上游，落潮歷時先增大后減小的趨勢不變，說明糙率不是洪季潮波變形拐點形成的主要原因。

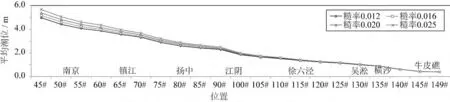
圖7 平均水位水面線變化Fig.7 The variation of mean water level

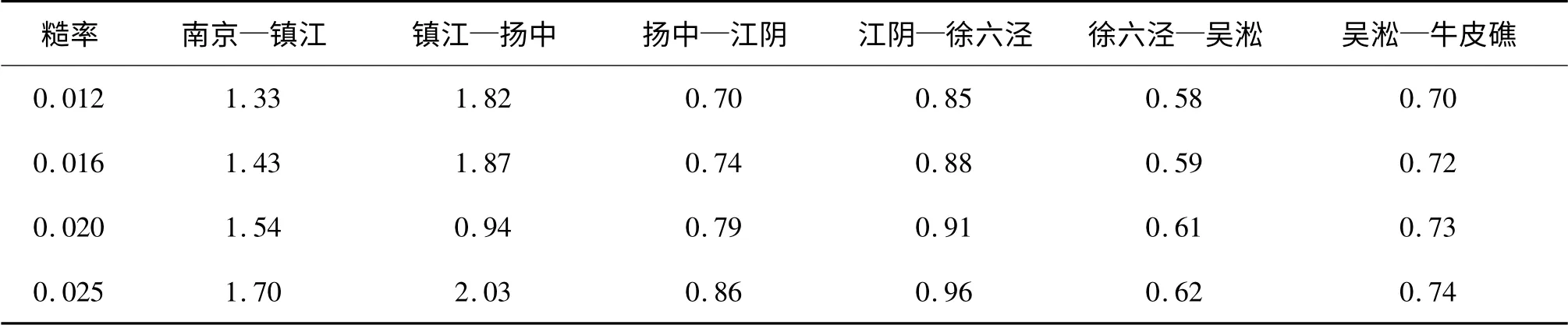
表5 糙率變化條件下長江感潮河段平均水位水面比降Tab.5 Mean water surface slope of different roughnesses in the Yangtze tidal reach (×10 －5)

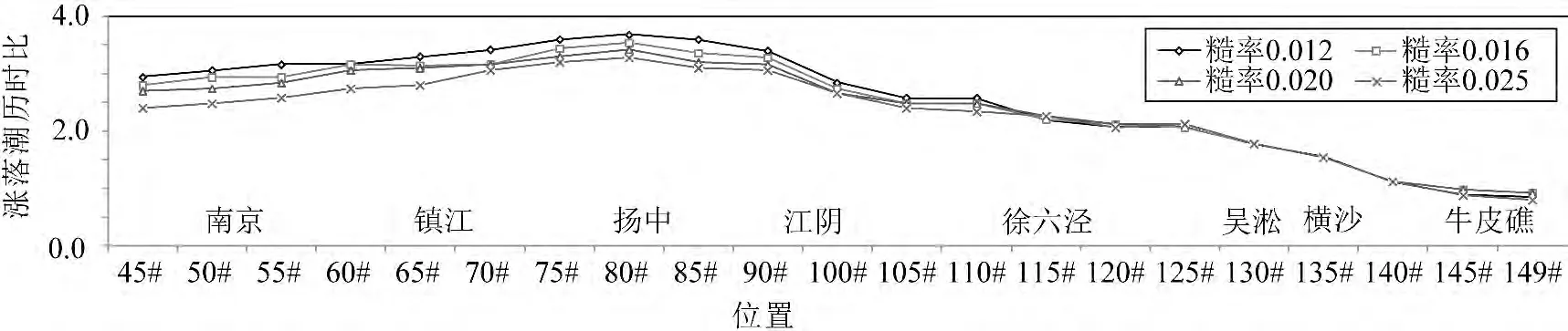
圖8 潮波變形對糙率變化的響應Fig.8 Tidal wave deformation caused by roughness changing

3.3 潮波變形對徑流的響應

徑流量在水位上的反映為水位隨徑流量的增大而升高，越往上游該現象越明顯(如圖9 所示)，因越往上游徑流作用越大，潮汐作用越弱，南京站徑流為10 000 m3/s 與90 000 m3/s 時，平均水位差超過7 m，北槽口外，潮汐作用為主，徑流作用微弱，故徑流變化后，該處平均水位變化微小。由此可見，徑流量的增大改變了長江河口平均水位的水面比降(表6)，越往上游，水面坡降增加越大。

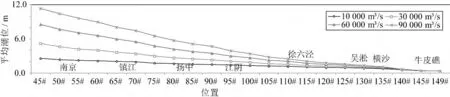
圖9 平均水位水面線變化Fig.9 The variation of mean water level

圖10 為潮波變形對徑流變化的響應。當徑流量為10 000 m3/s 時，自下游至上游，落潮歷時呈逐漸增大的趨勢，由于徑流量較小，徑流對潮波傳播阻力小，落潮歷時整體相對較短。徑流量增大到30 000 m3/s 時，落潮歷時整體大于徑流量為10 000 m3/s 時，且自下游至上游，落潮歷時出現先增大后減小的現象，拐點位于揚中附近。徑流量增大到60 000 m3/s 時，自下游至上游，落潮歷時出現先增大后減小的現象明顯，且轉折點向下游偏移至江陰上游，當徑流量增大到90 000 m3/s 時，拐點位于江陰附近。據路川藤［20］的研究，徑流量為30 000、60 000、90 000 m3/s 時，潮流界的位置位于炮子洲、天生港、白茆河處，潮波變形拐點均位于潮流界上游。潮流界下游，隨著徑流量的增大，潮波上溯阻力增大，落潮歷時延長。潮流界上游，隨著徑流量的增大，落潮歷時出現先增大后減小的現象愈趨顯著，拐點隨徑流量的增大向下游偏移。

表6 徑流變化條件下平均水位水面比降Tab.6 Mean water surface slope under different runoffs (×10 －5)

圖10 潮波變形對徑流量變化的響應Fig.10 The tidal wave deformation caused by changing runoff

3.4 潮波變形分析

前文研究了特定河道中，徑流及糙率對潮波變形的影響。經分析知，糙率對潮波變形的影響遠小于徑流，徑流量的大小在河道中主要反映為平均水位水面比降(圖9、表6)的變化，即平均水位水面比降的變化對潮波變形影響較大。

洪水期，潮波上溯過程中，潮波變形存在明顯的轉折點。對于轉折點以下河段，徑流量的增大致使潮波上溯阻力增大，潮波能量損耗多，潮波變形加劇。轉折點上游河段，潮波變形逐漸趨緩的現象難以用潮波理論解釋，下文試從力學角度解釋該現象。

假設徑流與潮波二者相互獨立，潮波疊加在徑流水面之上，潮波傳播在河道上反應為水面的升降。將平均水面線以上高潮位水體看作一個整體，高潮位水體在徑流水面向上游運動，其受自身重力和徑流向下游運動而產生的水流拖曳力及水面支持力，如圖11 所示。重力和水流拖曳力是高潮位向上游運動的阻力，可表示為:

式中:FH為高潮位水體向上游運動的阻力，f 為水流拖曳力，G 為重力，α 為平均水面與水平方向的夾角。

低潮位向上游傳播表現為水位的下降，若將平均水面線以下低潮位看作一個整體，則低潮位向上游運動只受徑流向下游運動而產生的水流拖曳力(設漲落潮過程中水流拖曳力不變):

式中:FL為低潮位水體向上游運動的阻力。

當α →0 時，FH→FL，說明平均水面比降越小，高潮位重力對潮波向上游傳播影響越小，相反，平均水面比降越大，高潮位重力對潮波向上游傳播影響越大。

洪水期，潮流界以上河段水面比降明顯大于潮流界以下河段(表6)，潮波變形程度受高低潮位潮波傳播速度差異和高潮位自身重力兩個因素影響。高、低潮位潮波傳播速度差異致使越往上游潮波變形越劇烈，高潮位自身重力致使越往上游潮波變形越趨緩;當高潮位自身重力對潮波傳播的影響大于高低潮位潮波傳播速度差異時，潮波變形趨緩;當高潮位自身重力對潮波傳播的影響小于高低潮位潮波傳播速度差異時，潮波變形繼續加劇。

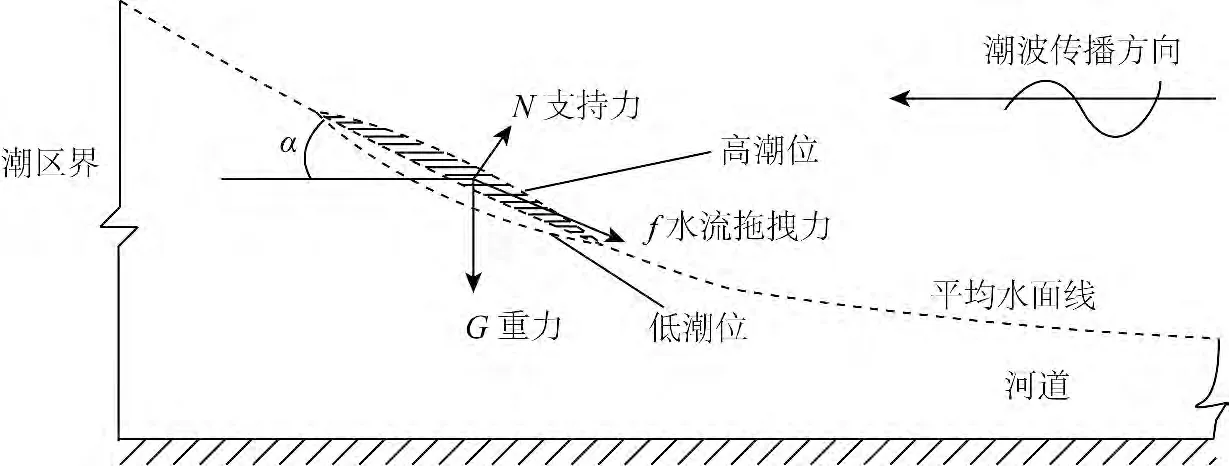
圖11 潮波傳播力學分析示意Fig.11 The force analysis of tidal wave propagation

4 結 語

1)據長江口實測水文資料分析，洪水期，潮波上溯過程中潮波變形先加劇后趨緩，枯水期這一現象不明顯。

2)基于非結構網格FVM 方法，研究了潮波變形對糙率和徑流量變化的響應。研究認為徑流量對潮波變形的影響遠大于糙率，徑流量對潮波變形的影響主要原因在于平均水位水面比降的變化。

3)據潮波上溯力學分析，認為潮流界以上水域，高潮位上溯傳播的阻力較大，當阻力對潮波傳播的影響大于潮差引起的高低潮位潮波傳播速度差異時，便造成了洪水期潮波變形先加劇后趨緩的特點。

［1］黃勝，盧啟苗.河口動力學［M］.北京:水利電力出版社，1992.(HUANG Sheng，LU Qimiao.Estuarine dynamics［M］.Beijing:Water Power Press，1992.(in Chinese))

［2］KOSUTH P，CALLEDE J，LARAQUE A.Ocean tide waves progagation along downstream amazon river:measuring the amazon discharge at the estuary［J］.Building Partnerships，2000(310):1-10.

［3］VAN RIJN C.Analytical and numerical analysis of tides and salinities in estuaries;part I:tidal wave propagation in convergent estuaries ocean dynamics［J］.Ocean Dynamics，2011，61(11):1719-1741.

［4］HUBERT H，SABENIJE G.Lagrangian solution of st.Venant’s equations for alluvial estuary［J］.Journal of Hydraulic Engineering，1992，118(8):1153-1163.

［5］HUBERT H，SABENIJE G.Determination of estuary parameters on basis of lagrangian analysis［J］.Journal of Hydraulic Engineering，1993，119(5):628-642.

［6］SABENIJE G，HUBERT H.Analytical expression for tidal damping in alluvial estuaries［J］.Journal of Hydraulic Engineering，1998，124(6):615-618.

［7］PAN Cunhong，LIN Bingyao，MAO Xianzhong.Case study:numerical modeling of the tidal bore on the Qiantang river，China［J］.Journal of Hydraulic Engineering，2007，133(2):130-138.

［8］BAO W，ZHANG X，YU Z，et al.Real-time equivalent conversion correction on river stage forecasting with manning’s formula［J］.Journal of Hydrologic Engineering，2011(1)，16:1-9.

［9］HASAN G，DIRK VAN M，CHEONG H，et al.Improving hydrodynamic modeling of an estuary in a mixed tidal regime by grid refining and aligning［J］.Ocean Dynamics，2011(11):1-15.

［10］路川藤.長江口潮波傳播［D］.南京:南京水利科學研究院，2009.(LU Chuanteng.The tidal propagation in Yangtze estuary［D］.Nanjing:Nanjing Hydraulic Research Institute，2009.(in Chinese))

［11］陳丕翔.基于有限體積法的二維水流水質模擬［D］.南京:河海大學，2007.(CHEN Pixiang.Water quanlity simulation based on 2D finite volume method［D］.Nanjing:Hohai University，2007.(in Chinese))

［12］惲才興.圖說長江河口演變［M］.北京:海洋出版社，2010.(YUN Caixing.The Yangtze river estuary evolution［M］.Beijing:Ocean Press，2010.(in Chinese))

［13］肖慶華，岳志遠，劉懷漢，等。長江下游二維淺水非恒定流數值模擬［J］.水力發電學報，2013，32(5):115-121.(XIAO Qinghua，YUE Zhiyuan，LIU Huanhan，et al.Numerical simulation of unsteady 2D shallow water flow of the lower Yangtze river［J］.Journal of Hydroelectric Engineering，2013，32(5):115-121.(in Chinese))

［14］夏云峰.一種簡便的非交錯曲線網格三維水流數值模型［J］.水動力學研究與進展，2002，17(5):638-646.(XIA Yunfeng.A simplified 3D flow model for natural river with curvilinear collocated grids［J］.Journal of Hydrodynamics，2002，17(5):638-646.(in Chinese))

［15］梁婷.長江河口洲灘高強度開發水動力響應研究［D］.南京:南京水利科學研究院，2011.(LIANG Ting.The study of hydrodynamic response on Yangtze estuary segment beach high-intensity development［D］.Nanjing:Nanjing Hydraulic Research Institute，2011.(in Chinese))

［16］李健鏞.長江大通—徐六涇河段水沙特征及河床演變研究［D］.南京:河海大學，2007.(LI Jianyong.Study on the evolution and sediment characteristics in the Datong-Xuliujing River［D］.Nanjing:Hohai University，2007.(in Chinese))

［17］曾小輝，李國杰，姜昱.長江感潮河段平面二維潮流數值模擬［J］.水運工程，2012(4):12-16.(ZENG Xiaohui，LI Guojie，JIANG Yu.Numerical solution of 2-D tidal flow of the estuary in the Yangtze river［J］.Port ＆Waterway Engineering，2012(4):12-16.(in Chinese))

［18］竇希萍，李褆來，竇國仁.長江口全沙數學模型研究［J］.水利水運科學研究，1999(2):136-145.(DOU Xiping，LI Tilai，DOU Guoren.Numerical model study on total sediment transport in the Yangtze River estuary［J］.Hydro-Science and Engineering，1999(2):136-145.(in Chinese))

［19］馬進榮，陳志昌.長江口風暴潮流場計算［J］.水利水運工程學報，2003(1):35-39.(MA Jinrong，CHEN Zhichang.Simulation of storm surge current in the Yangtz Estuary［J］.Hydro-Science and Engineering，2003(1):35-39.(in Chinese))

［20］路川藤.長江口潮波傳播模擬研究及主要影響因素分析［D］.南京:南京水利科學研究院，2013.(LU Chuanteng.The simulation of tidal propagation in Yangtze estuary and the analysis of its main influencing factors［D］.Nanjing:Nanjing Hydraulic Research Institute，2013.(in Chinese))

［21］沈煥庭，李九發.長江河口水沙輸運［M］.北京:海洋出版社，2011.(SHEN Huanting，LI Jiufa.Water and sediment transport in the Yangtze estuary［M］.Beijing:Ocean Press，2011.(in Chinese ))