斷裂參數的數值計算方法分析
劉丹丹,李曉川
(沈陽工業大學建筑工程學院,遼寧 沈陽 110870)
從20世紀50年代開始,固體力學的一個分支斷裂力學快速發展了起來,并為現代化的生產提供了理論依據。半個多世紀過去了,斷裂力學[1]這一領域的知識理論已經發展的相當成熟。斷裂力學有助于人們認識和理解材料中裂紋的產生、擴展和最終破壞的過程,并為結構損傷容限設計提供理論基礎。
斷裂力學中的3個基本斷裂參數是應力強度因子、路徑無關積分(J積分)和應變能釋放率。應力強度因子的計算主要依賴于裂紋前端的局部應力場,它描述了彈性裂紋尖端應力場的強弱。J積分描述的是由于裂紋的存在所吸收的能量,而能量釋放率是描述產生新的裂紋面所需要的能量。這兩個基于能量的參數是等價[2]的。隨著計算機硬件和軟件的迅速發展,用數值方法計算斷裂參數就變的切實可行。很多數值方法被嘗試應用于斷裂參數的計算,如有限差分法、邊界元法和發展起來的無網格法,但是由于缺少軟件的支持,這些方法應用實例相對缺乏。而有限元法成功的應用于很多工業部門,并發展了針對三個基本斷裂參數的數值計算技術。用應力或應變外推法計算應力強度因子,等效積分區域技術計算J積分,全局或者局部的虛擬裂紋擴展技術和虛擬裂紋閉合法計算應變能釋放率。
1 外推法
1.1 基于應力的外推法
對于線彈性材料,應力在裂紋尖端處是趨于無窮大的,也就是應力奇異性。所以網格尺寸越小,裂紋前端單元內的積分點的應力值就會越大。從這可以知道,應力值對于網格的尺寸是不收斂的。于是引入了應力強度因子的概念來克服由于應力奇異帶來的數學上的困擾,用來描述裂紋尖端附近應力的強弱。外推法是借助于有限元的方法來計算應力強度因子,在有限元分析中,裂尖前面的單元里積分點上的應力值以及其對應的積分點坐標值是很容易就可以直接讀出的。雖然無法用數值方法直接計算裂尖處的應力強度因子,可是裂尖前端那些非奇異的應力值卻是可知的。對于每一個ri(距離裂紋尖端的極半徑)大于零都有一個非奇的應力值σyi和對應的KIi:KIi=σyi,然后可以構造數據對(ri,KI)i,用最小二乘法擬合數據點。在這里假定了兩者之間線性關系為:
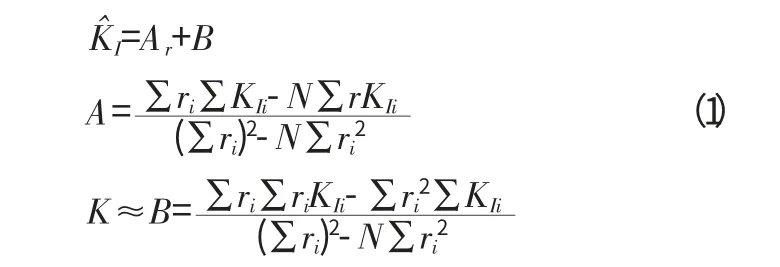
上式中的N 是外推法所采用的數據對象,其截距的物理意義就是所要計算的應力強度因子。
可是這個方法存在幾個問題。第一,沒有明確規定采取多少對數據點進行外推計算得到最后的精度高。一般情況下是采用許多點直至KI對N 收斂于某個值才行。第二,靠近裂尖處的數據反而是引起誤差的主要來源,而相反的距離裂尖越遠越滿足線性的假設,這樣使得外推法所采用的點往往不包括貼近裂尖的點,說明線性外推對裂尖來說并不很精確,而在斷裂分析中又恰好最應該多關注裂紋尖端,因為應力強度因子的作用就是描述裂尖應力信息,計算一個用來描述裂尖應力場的量所采用的方法卻不能依靠裂尖信息,而必須用遠場數據來計算,這在邏輯上存在悖論。
1.2 基于應變的外推法
在很多的商業軟件中,位移是求解的基本變量,而應力是通過應變和位移聯系起來是次要的變量,所以位移的外推法的計算精度要高。對于確定的距離裂紋尖端r 處,裂紋后端垂直位移v 的數據可以在有限元分析中直接讀取。和基于應力的外推法一樣,也可以構造數據對(ri,KIi):
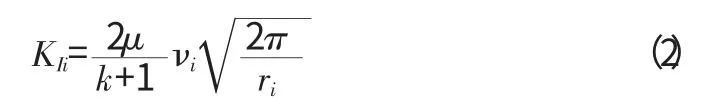
然后利用最小二乘法來擬合數據點,得到相應的應力強度因子數值。同樣的,基于應力的外推法存在的問題也存在于此方法中。如果想解決問題,使用多項式外推應該是最直接的方法,可是并不是所有的情況都存在確定的多項式。因此,引入奇異單元和疊合單元[3]理論上在裂尖處采用這些單元,在其他區域采用常規的單元,可以極大地減少網格的數量同時保持計算精度。然而采用這些單元在使用時非常的不方便,尤其是對于裂紋擴展的問題,而且適用范圍也很有限,無法滿足實際情況多樣性和復雜性的需求。
2 等效積分區域法
J積分是由Rice[4]提出來的一個處理非線性斷裂問題的斷裂參數,這個參數的引入是基于能量守恒的概念,因此對裂紋尖端應力奇異性的依賴程度比較弱,不需要對裂紋尖端處的單元進行特殊的處理,而是從全局的角度分析處理斷裂問題。J積分的數學表達式為:
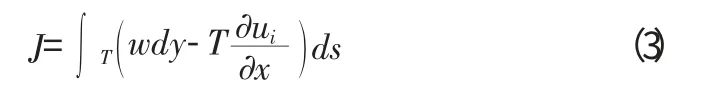
上式中,ui是位移矢量的分量;ds是沿著積分路徑的微小增量;w 是應變能密度因子,其定義是:

上式中σij和εij分別是應力張量和應變張量。
由于Rice證明了J積分的數值不隨著積分回路的改變而改變,因此它也叫做路徑的無關積分。在這里可以看到J積分的表達式中,只有應力、應變和位移三場沒有材料屬性。但是在計算應力的時候是需要用到材料各向同性或者異性的本構關系。所以,這個表達式只是使用于一般的熱彈塑性和各向異性材料的問題。實際上這個表達式并不適用于數值計算,為此Shih和Raju[5]等人提出了等效積分區域法來達到對J積分進行數值計算。基于用裂尖附近的一個有限區域來代替積分回路進行J積分計算的思想,表達式可以轉化為:
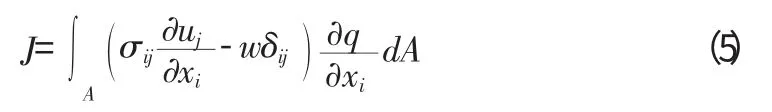
上式中δij是Kronic函數,q 是輔助函數,它只是一個數學處理,目的是為了讓積分表達式更利于采用數值計算方法。J積分是遠場回路積分,它具有較好的精度,也不需要對裂尖處的單元進行特殊處理,不過由于沒有分離斷裂模式,對于混合斷裂型問題而言,還需要額外處理才能進行完整的分析。就算對于平面問題,它的計算過程都顯得相當的復雜。所以盡管它能夠用于裂紋擴展問題但是實際上操作很不方便,而且在有限元的分析中實用性很低。
3 虛擬裂紋擴展法
3.1 全局的虛擬裂紋擴展法
Irwin[6]提出了應變能釋放率的概念。考慮有一個厚度為B的二維裂紋體,其裂紋長度是a,那么應變能釋放率就是產生面積為ΔA 的新裂紋面所需要的能量,于是:
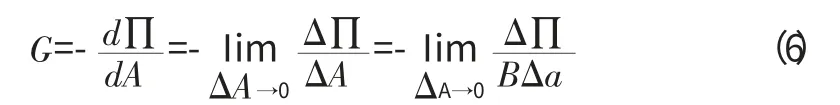
上式中∏=U-W 是裂紋體的勢能,U 是裂紋體的應變能,W是外力功,Δa 是裂紋的微小擴展量。
從上式可以看出,應變能釋放率的計算要求Δa 趨近于零,很明顯對于有限元分析這種數值方法來說,無法達到這個極限。所以,采用兩步分析過程的虛擬裂紋擴展法。在第一步的分析中,通過有限元分析獲得裂紋長度是a 的裂紋體的勢能(∏1=U1-W1);第二步分析中,通過有限元分析獲得裂紋長度是a+Δa 的裂紋體的勢能(∏2=U2-W2)。若和網格尺寸相關的Δa足夠小,那么就可以很好的將應變能釋放率近似為:

全域虛擬裂紋擴展法有一個局限性就是只能夠得到總的應變能釋放率,不能分離斷裂模式。
3.2 局部的虛擬裂紋擴展法
基于將裂紋閉合一個微小的擴展增量所需要的功和勢能的改變是等效的這一思想,可以用裂紋的閉合積分來計算裂尖的能量釋放率,則局部的形式為:

其中應變能分量為:
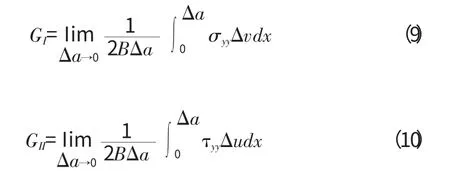
假設裂紋的方向是沿著X 軸方向,σyy是張開斷裂模式中沿著閉合裂紋面上的法向應力,txy是滑移模式中沿著閉合裂紋面上的切向應力。Δu 和Δv 是閉合裂紋張開后裂尖后面閉合裂紋面上的位移分量。上兩式可以用兩個步驟的分析過程計算出來。如果網格尺寸相關的Δa 很小,就可以將應變能釋放分量近似為:
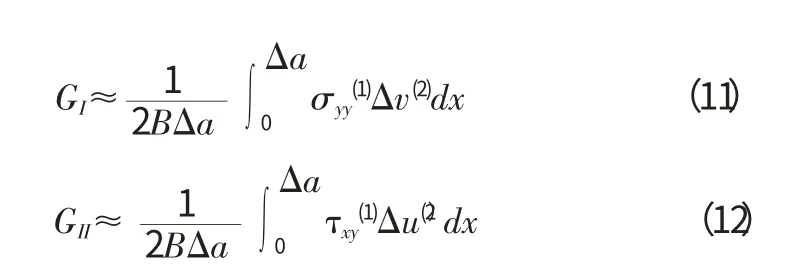
如果直接用上兩式計算應變能釋放率分量則需要節點上的應力值,因為公式中是沿著閉合裂紋線對應力進行數值積分而閉合裂紋線一般位于有限元單元的邊上。在有限元分析中,當把應力外推到單元的節點上,或者當單元接近裂紋尖端時,所得到的應力時非常不精確的。為了避免使用不精確的應力值,采用節點力來代替應力的積分。用節點力和節點位移計算出的應變能釋放率為:
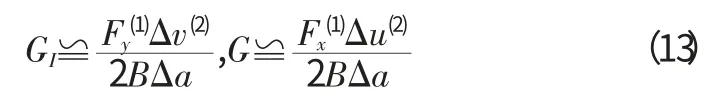
用節點力和節點位移計算應變能釋放率有很多的優點是:①公式中只有節點力和節點位移這兩個基本變量,任何有限元計算的商業軟件都可以直接輸出;②公式不需要對應力進行數值積分,這樣減少了計算量;③有限元網格尺寸的影響小,為了保證近似精度,需要采用合理的網格密度,但是用比較粗糙的網格也能獲得令人滿意的結果;④無論是線性的還是非線性的材料都可以采用這個方法。
而此方法的缺點是分析過程必須是2步,且裂紋長度在這兩步中是不同的,這樣增加了網格準備工作量,尤其對于三維問題時,同時,對于裂紋擴展問題,由于需要用上一步的計算結果來不斷的準備新的網格,使得研究起來相當的不方便。
4 虛擬裂紋閉合法
為了避免虛擬裂紋擴展法的不便之處。Rybicki和Kanninen提出[7]適用于二維平面問題的一步分析法即修正的裂紋閉合積分,也就是后來的虛擬裂紋閉合法。
虛擬裂紋閉合法的基本假設是虛擬裂尖和實際裂尖后面張開位移近似相同。于是,公式轉化為:
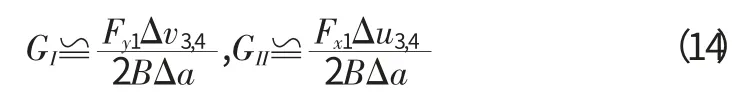
其中,Fy1和Fx1為裂紋尖端節點Y 和X 方向的節點力;Δu3,4和Δv3,4為緊挨裂紋尖端后面節點在X 和Y 方向的相對位移;B 為裂紋體的厚度。Δa 為裂紋尖端前面的虛擬裂紋擴展量。
虛擬裂紋閉合法在保留了虛擬裂紋擴展法的所有優點的同時,克服了它的所有缺點,只要求一步的有限元分析。這使得此方法有很大的吸引力,尤其是那些用有限元計算商業軟件對斷裂問題進行分析研究的工程師們。
5 結 論
由上述分析可知,在結合有限元分析斷裂問題的數值計算方法中,虛擬裂紋閉合法非常簡便高效。
[1]丁遂棟.斷裂力學[M].北京:機械工業出版社,1991.
[2]沈成康.斷裂力學[M].上海:同濟大學出版社,1996.
[3]Blandford,G.E..Two-dimensional stress intensity factor computations using the boundary element method.International Journal for Numerical Methodsin Engineering,1981.
[4]Rice,J.R..APath Independent Integral and the Approximate Analysis of Strain Concentration by Notches and Cracks,Journal of Applied Mechanics,1968.
[5]Moura,B.,and Shih,C.F..A Treatment of Crack Tip Contour Integrals.International Journal of Fracture,1987.
[6]Irwin GR.Crack-extension forcefor a part-through crack in aplate.J Appl Mech,1962.
[7]Rybicki EF,Kanninen MF.A finite element calculation of stress intensity factors by a modified crack closure integral.Engineering Fracture Mechanics,1977(9).

