非自治逆緊系統的拓撲壓
張秀芬,郭亞曉,楊宇
(西北大學數學學院,陜西 西安710127)
非自治逆緊系統的拓撲壓
張秀芬,郭亞曉,楊宇
(西北大學數學學院,陜西 西安710127)
主要研究了非自治逆緊系統上的拓撲壓.給出了非自治逆緊系統上拓撲壓的定義,得到了這種拓撲壓關于集合Z的一些性質,并在同胚意義下,探討了兩個非自治逆緊系統上拓撲壓的大小關系.
C-P結構;容許覆蓋;非自治逆緊系統;拓撲壓
1 引言
拓撲壓在熱力學中有著廣泛應用.長期以來,在熱力學形式與維數理論的相關領域,探究拓撲壓及其變分原理是研究的熱點課題之一.1973年,文獻[1]對緊度量空間上的擴張映射給出了拓撲壓的概念;1975年,文獻[2]又對緊度量空間上的連續自映射定義了拓撲壓,并建立了拓撲壓的變分原理.受文獻[3]的啟發,2011年,文獻[4]中又對拓撲壓作了進一步研究.上述工作討論的都是緊致系統上的拓撲壓和變分原理.2014年,文獻[5]討論了在非緊集上逆緊映射的拓撲熵及其變分原理.由于空間可能出現非緊的情況,且基于拓撲壓是拓撲熵概念的推廣,因此,本文在其框架下給出了非自治逆緊系統上拓撲壓的相關概念和性質.
2 預備知識
下面,先給出本文中需要的一些基本概念和記號.首先給出C-P結構的定義.
定義2.1[3]設X和S是兩個任意的集合,F={Us:s∈S}是X的子集族.假設存在兩個函數η,ψ:S→R+滿足以下條件:
(1)存在s0∈S使得Us0=?;如果Us=?,那么η(s)=0,ψ(s)=0;如果Us/=?,那么η(s)>0,ψ(s)>0;
(2)對任意的δ>0,存在ε>0,只要s∈S滿足ψ(s)≤ε,就有η(s)≤δ.
(3)對任意的ε>0,存在有限或可數的集合G?S覆蓋X(即)而且滿足ψ(G):=sup{ψ(s):s∈G}≤ε.
令ξ:S→R+是一個函數.若集合S、子集族F、及函數ξ,η,ψ滿足條件(1)-(3),則稱其構成了X上的一個C-P結構τ,并記τ=(S,F,ξ,η,ψ).

定義2.2[6]設X是一個拓撲空間,如果f:X→X是一個連續映射,且任意緊集在f下的原象是緊集,則稱f為逆緊映射.
定義2.3[6]如果一個開集的補集或閉包是緊集,則稱這個開集為容許開集.
定義2.4[6]如果拓撲空間X的有限開覆蓋U滿足對任意的A∈U,A是一個容許開集,則稱開覆蓋U為容許覆蓋.
定義2.5設X為拓撲空間,對于任意i∈Z+,映射fi:X→X為逆緊映射,則稱(X,f1,∞)為非自治逆緊系統.
注2.1緊度量空間中的任何連續映射都是逆緊映射,且緊拓撲空間的任何開覆蓋都有容許子覆蓋.
下面在非自治逆緊系統中定義拓撲壓,上、下容量拓撲壓.
設(X,f1,∞)為非自治逆緊系統,φ:X→R為連續函數,U是X的一個容許覆蓋.記
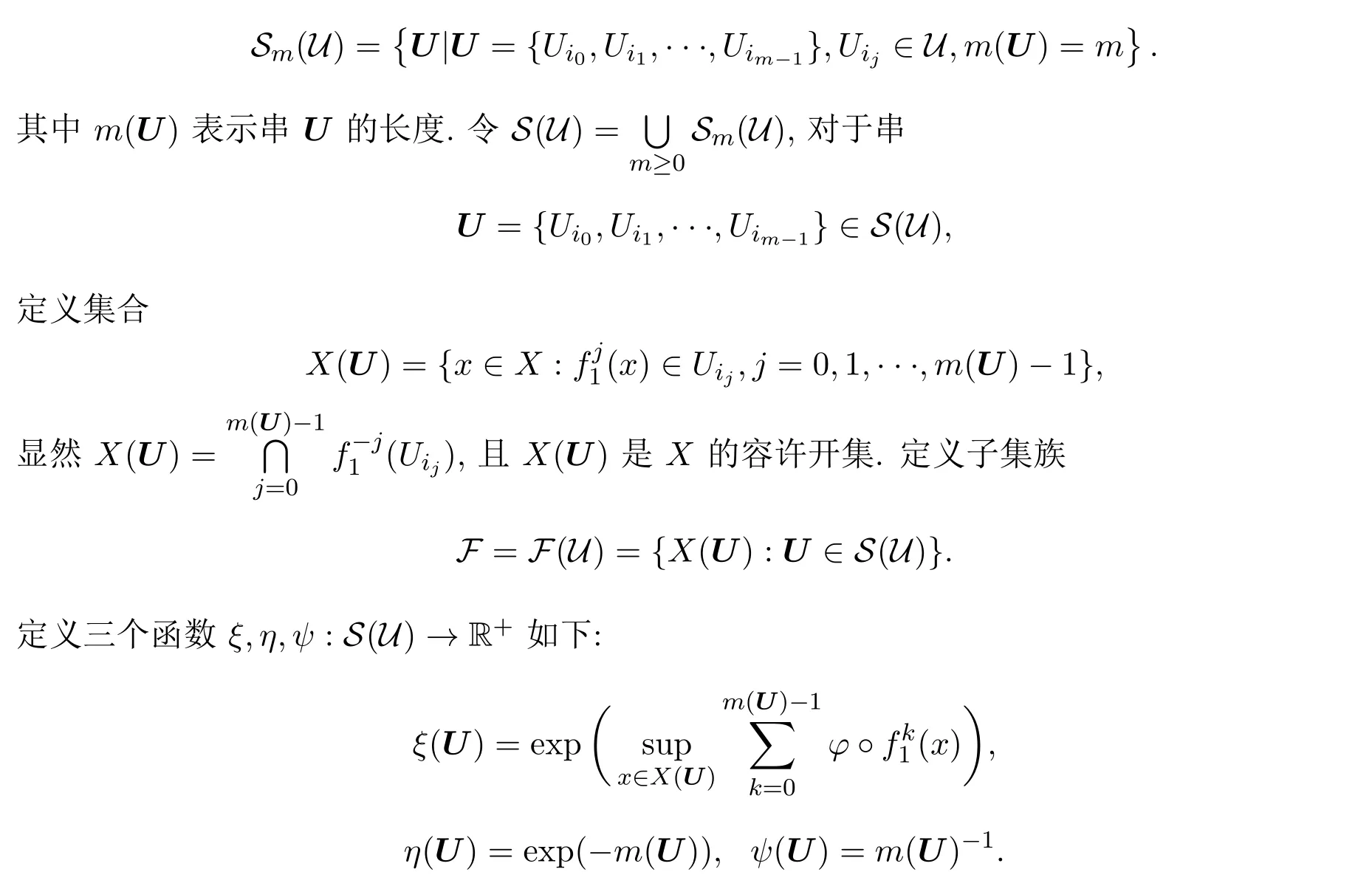

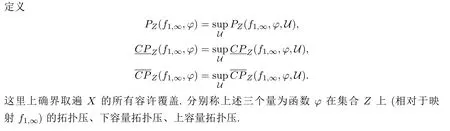
3 主要結果及其證明
定理3.1設(X,f1,∞)為非自治逆緊系統,那么關于拓撲壓有以下性質:



定理3.2設(X,f1,∞)為非自治逆緊系統,那么關于下、上容量拓撲壓有以下性質:
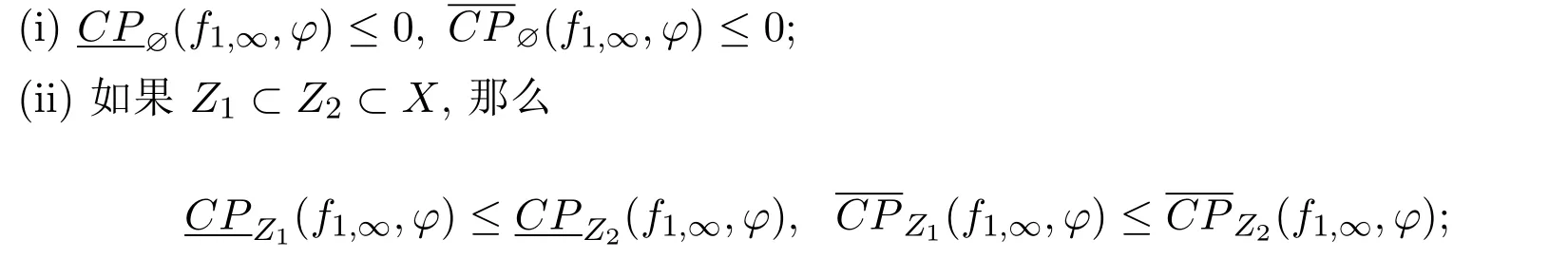

定理3.3設(X,f1,∞),(Y,g1,∞)都是非自治逆緊系統,φ:X→R為連續函數.如果f1,∞和g1,∞是拓撲共軛,存在同一個同胚π:X→Y,對于任意i∈Z+都有π?fi=gi?π,那么PZ(f1,∞,φ)=PπZ(g1,∞,φ?π-1).

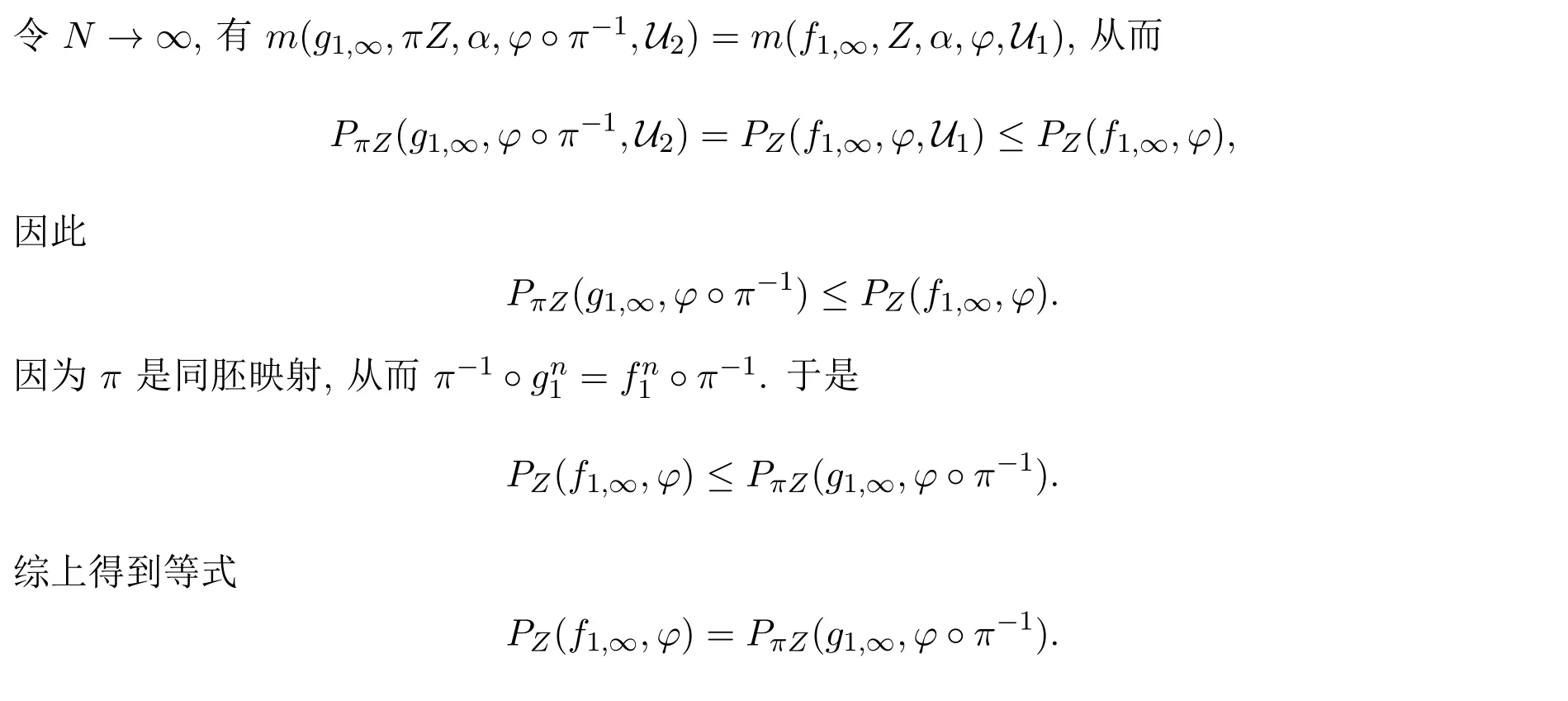
[1]Ruelle D.Statistical mechanics on a compact set with action satisfying expansiveness and specification[J]. Trans.Amer.Math.Soc.,1973,185:237-251.
[2]Walters P.A variational principle for the pressure of continuous transformations[J].Amer.J.Math.,1976,97:937-971.
[3]Pesin Y.Dimension Theory in Dynamical Systems[M].Chicago:the University of Chicago Press,1997.
[4]Barreia L.Thermodynamic Formalism and Applications to Dimension Theory[M].Basel:Birk¨auser,2011.
[5]Ma Dongkui,Cai Bin.Topological entropy of proper map[J].Taiwanese Journal of Mathematics,2014,18(4):1219-1241.
[6]Patr~ao M.Entropy and its variational principle for non-compact metric spaces[J].Ergodic Theory Dynam. Systems,2010,30:1529-1542.
[7]Bowen R.Topological entropy for noncompact sets[J].Trans.Amer.Math.Soc.,1973,184:125-136.
The topological pressure of a non-autonomous proper system
Zhang Xiufen,Guo Yaxiao,Yang Yu
(College of Mathematics,Northwest University,Xi′an710127,China)
This paper focuses on the topological pressure of a non-autonomous proper dynamical system.First of all,giving the definition of topological pressure,and we got some properties of subset Z,then in the case of homeomorphism,we explore the relationship between topological pressures of two non-autonomous proper dynamical systems.
C-P structure,admissible cover,non-autonomous proper system,topological pressure
O177.91
A
1008-5513(2015)04-0373-07
10.3969/j.issn.1008-5513.2015.04.006
2014-01-30.
國家自然科學基金(11301417).
張秀芬(1990-),碩士生,研究方向:拓撲動力系統與遍歷論.
2010 MSC:60F15

