（3+1）維短波方程的不變子空間和精確解

殷京津，王麗真

（1.寧波大學(xué)理學(xué)院，浙江 寧波315211；2.西北大學(xué)數(shù)學(xué)學(xué)院，陜西 西安710127）

（3+1）維短波方程的不變子空間和精確解

殷京津1，王麗真2

（1.寧波大學(xué)理學(xué)院，浙江 寧波315211；2.西北大學(xué)數(shù)學(xué)學(xué)院，陜西 西安710127）

利用不變子空間方法研究了（3+1）維短波方程的不變子空間和精確解.在（2+1）維短波方程增加一維的情形下，構(gòu)造了更加廣泛的精確解，同時(shí)也得到了超曲面的爆破解.主要結(jié)果不僅推廣了不變子空間理論在高維非線性偏微分方程中的應(yīng)用，而且對研究高維方程的動(dòng)力系統(tǒng)有重要意義.

不變子空間；短波方程；精確解；高維非線性偏微分方程

1 引言

在偏微分方程理論的研究中，偏微分方程的精確解和解的正則性是人們所關(guān)心的兩個(gè)方面，特別是精確解的研究，它幾乎貫穿整個(gè)偏微分方程理論的研究.恰當(dāng)?shù)木_解能夠最優(yōu)地描述出局部和全局泛函類、唯一性的泛函類以及有適定的漸近行為的泛函類.不變子空間方法作為求解非線性偏微分方程的方法之一［1］，2007年文獻(xiàn)［2］系統(tǒng)地研究了非線性偏微分方程的不變子空間和精確解.近年來，許多學(xué)者運(yùn)用不變子空間方法研究了其他實(shí)際模型的精確解［3-6］.同樣，運(yùn)用不變子空間方法求解高維非線性偏微分方程［7-8］，也是一個(gè)很值得探討的問題.

1958年，Khristianovich和Ryzhov提出了（2+1）維的短波方程：

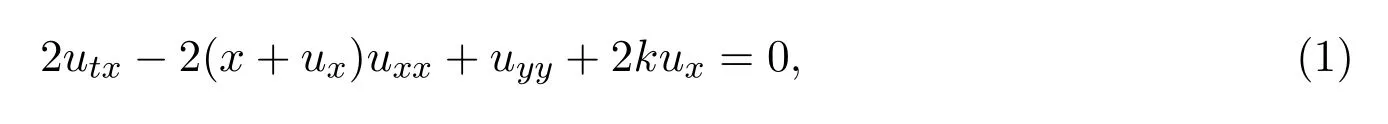
它的發(fā)現(xiàn)是與非線性弱激波的反射相聯(lián)系的［9］.文獻(xiàn)［10］研究了該方程的對稱群和守恒律.文獻(xiàn)［11］利用穩(wěn)定區(qū)域的方法求解了對于實(shí)常數(shù)時(shí)的（2+1）維短波方程的精確解.

本文考慮（3+1）維短波方程：它是對（2+1）維短波方程自變量擴(kuò)展一維得到的，也可以看作是對（2+1）維短波方程的推廣.

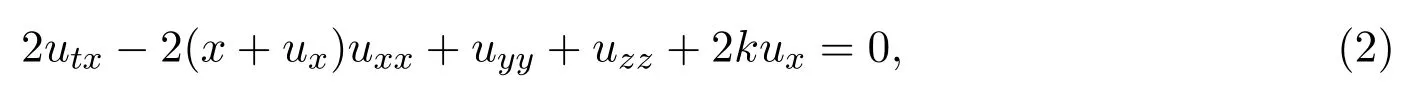
在第一節(jié)中，本文介紹了非線性算子所允許的不變子空間以及方程的廣義分離變量解，并給出了（3+1）維短波方程的不變子空間.在第二節(jié)中，應(yīng)用不變子空間的方法給出了對于任意實(shí)常數(shù)k的（3+1）維短波方程的精確解，這也是本文研究的意義所在.文中的計(jì)算過程和結(jié)論推廣了不變子空間理論在高維非線性偏微分方程中的應(yīng)用，這對于研究高維方程的動(dòng)力系統(tǒng)產(chǎn)生了重要意義.

2 非線性算子的不變子空間

考慮一般的演化方程：

3 （3+1）維短波方程的精確解

利用不變子空間方法，方程（2）關(guān)于x的多項(xiàng)式有如下形式的解：

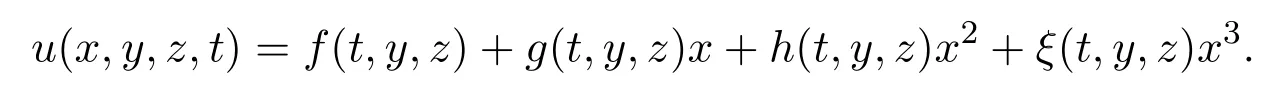
將（58）式代入方程（55）式，然后積分得到

其中，w0是確定的復(fù)變量，χ（t，μ）和υ（t，μ）是關(guān)于t的復(fù)函數(shù)，在復(fù)變量μ上是bar-同態(tài)的.

注3.1對于定義3.1的bar-同態(tài)函數(shù)，三角函數(shù)，實(shí)系數(shù)的多項(xiàng)式函數(shù)以及具有bar-不變周期的橢圓函數(shù)都是bar-同態(tài)函數(shù)，（40）式中的拓展函數(shù)F（t，μ）在μ上也是bar-同態(tài)的.

注3.2對于上述定理中的解，方程（2）還有如下形式的簡單解

定理3.2對于平凡解ξ=0，方程（2）有關(guān)于x的多項(xiàng)式的解u=f+gx+hx2，這里，h，g，f分別由（61）式、（62）式和（63）式給出.其中，式中所包含的σ（t，μ），ρ（t，μ），κ（t，μ），ω（t，μ），χ（t，μ）和υ（t，μ）都是關(guān)于實(shí)變量t和復(fù)變量μ的復(fù)函數(shù).如果σ，ρ，κ，ω，χ和υ都是光滑（解析）的，那么所得到的解也是光滑（解析）的.特別地，方程（2）中關(guān)于x，y和z的任意解一定具有這樣的形式.

4 結(jié)論

本文利用不變子空間方法，求出了（3+1）維短波方程的不變子空間和精確解，同時(shí)得到了比（2+1）維更廣泛的解，即對于任意的實(shí)常數(shù)k的精確解.在本文的基礎(chǔ)上，還可以思考運(yùn)用不變子空間求更高維的非線性演化方程的解時(shí)，方程的精確解有什么變化.同時(shí)，對于如何找到高維的非線性演化方程的不變子空間，也是在今后的工作中值得研究的問題.

［1］Galaktionov V A.Invariant subspaces and new explicit solutions to evolution equations with quadratic nonlinearities［J］.Proc.Roy.Soc.Edinburgh，1995，125：225-246.

［2］Galaktionov V A，Svirshchevskii S R.Exact solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics［M］.London：Chapman and Hall/CRC，2007.

［3］Qu C Z，Ji L N.Invariant subspaces and conditional Lie-B¨acklund symmetries of inhomogeneous nonlinear diffusion equations［J］.Sci.China.Math.，2013，56：2187-2203.

［4］Ji L N，Qu C Z.Conditional Lie-B¨acklund symmetries and invariant subspaces to nonlinear diffusion equation［J］.IMA.J.Appl.Math.，2011，76：610-632.

［5］Ji L N，Qu C Z.Conditional Lie-B¨acklund symmetries and invariant subspaces to nonlinear diffusion equation with convection and source［J］.Stud.Appl.Math.，2013，76：266-301.

［6］Sahadevan R，Bakkyaraj T.Invariant subspaces method and exact solutions of certain nonlinear time fractional partial differential equations［J］.Fractional Calculus and Applied Analysis，2015，18：146-162.

［7］左蘇麗，李吉娜，黃晴.（2+1）維擬線性方程的不變集和精確解［J］.西北大學(xué)學(xué)報(bào)：自然科學(xué)版，2007，37（6）：974-976.

［8］屈改珠.利用不變集方法求（2+1）維擬線性擴(kuò)散方程的精確解［J］.西北大學(xué)學(xué)報(bào)：自然科學(xué)版，2010，40（4）：576-578.

［9］Khristianovich S A，Ryzhov O S.On nonlinear reflection of weak shock waves［J］.Prikl.Mat.Tek.，1958，22（5）：586-599.

［10］Kucharczyk P.Group properties of equations of short waves in gas dynamics［J］.Bull.Acad.Pol.Sci.Ser. Sci.Technol.，1965，13（5）：469-477.

［11］Xu X P.Stable-range approach to the equation of nonstationary transonic gas flow［J］.Quart.Appl.Math.，2007，65：529-547.

Invariant subspaces and exact solutions of（3+1）dimensional short wave equation

Yin Jingjin1，Wang Lizhen2
（1.Faculty of Mathematics，Ningbo University，Ningbo315211，China；2.Department of Mathematics，Northwest University，Xi′an710069，China）

Considered herein is invariant spaces and exact solutions of（3+1）dimensional short wave equation with the invariant spaces method.More exact solution and hyperspace blow-up solution are obtained in case of increasing one dimension for（2+1）dimensional short wave equation.The results not only extend the application of the theory of invariant subspace in high-dimensional nonlinear partial differential equations，but also have a great meaning for study high-dimensional dynamical system equations.

invariant spaces，exact solutions，exact solutions，short wave equation，high-dimensional nonlinear partial differential equations

O175.29

A

1008-5513（2015）04-0403-11

10.3969/j.issn.1008-5513.2015.04.009

2015-05-10

國家自然科學(xué)基金（11201371）.

殷京津（1989-），碩士生，研究方向：偏微分方程及其應(yīng)用.

王麗真（1972-），博士，教授，研究方向：非線性偏微分方程的研究.

2010 MSC:35R5