基于多目標遺傳算法的汽車散熱器裝芯機排管部基座的優化設計

張 圓，周 海

ZHANG Yuan1，ZHOU Hai2

（1.江蘇大學 機械工程學院，鎮江 212013；2.鹽城工學院 機械工程學院，鹽城 224051）

0 引言

汽車零部件尤其是汽車散熱器的需求量迅速增長，帶動了國內汽車散熱器芯體生產企業數量上的增長。截至目前，國外企業仍牢牢掌控全自動芯體裝配機（簡稱裝芯機）的核心技術，國內企業只能花高價采購整機，掌握不到現有技術[1]。裝芯機主要由三個部分組成，分別是排管部、轉運部和壓裝部。本文是在聯合江蘇康杰機械股份有限公司研發設計的第一代裝芯機的基礎上，針對排管部過重的問題，以基座為對象，減輕其重量和提高其剛度為多目標的優化設計。目前，對于多目標優化問題，多目標遺傳算法（Multi-Objective Genetic Algorithm，MOGA）[2]能夠快速有效地獲得Pareto最優解集，如孫偉[3]等以UH-1H直升機為對象，采用多目標遺傳算法，引入個體的序和密度的概念使得搜索到的Pareto解集，更具有貼近性、均勻性和完整性。顧春榮[4]等采用響應面與多目標遺傳算法相結合來進行印制電子噴印機的結構優化，可以控制系統的不確定因素，保證結果最終優化的可靠性。

本文簡要介紹了多目標遺傳算法和響應面方法，制定了全自動汽車散熱器裝芯機排管部基座的優化設計路線：以基座的剛度和重量為優化目標，基于ANSYS Workbench，利用多目標遺傳算法，調整基座結構的關鍵參數，搜尋其優化設計的最優解。

1 多目標優化算法

1.1 多目標優化問題

在工程實踐和科學研究中，目標函數超過一個并且需要同時處理的最優化問題，即多目標優化問題。多目標優化問題一般具有n個設計變量，m個目標變量，表述如下：

式中，為n維的設計變量；為m維的目標變量；為映射函數；定義了p個不等式約束；定義了q個等式約束。

在多目標優化問題中，某解對于某個目標而言是好的，但對于其他目標卻可能較差，因此一般不存在一個最優解能同時使所有目標達到最優。一般都是取一個折衷的集合，稱為Pareto最優解集（或非支配解集）[5]。這些最優解需要決策者根據工作經驗、設計要求折衷處理，選出一個解作為問題的最優解。

1.2 多目標遺傳算法

多目標遺傳算法是在一次優化過程中搜尋大量多目標優化問題的Pareto最優解，是將生物進化理論應用于現代優化設計中，具有高效性、魯棒性好的特點[6]。其基本流程圖如圖1所示。

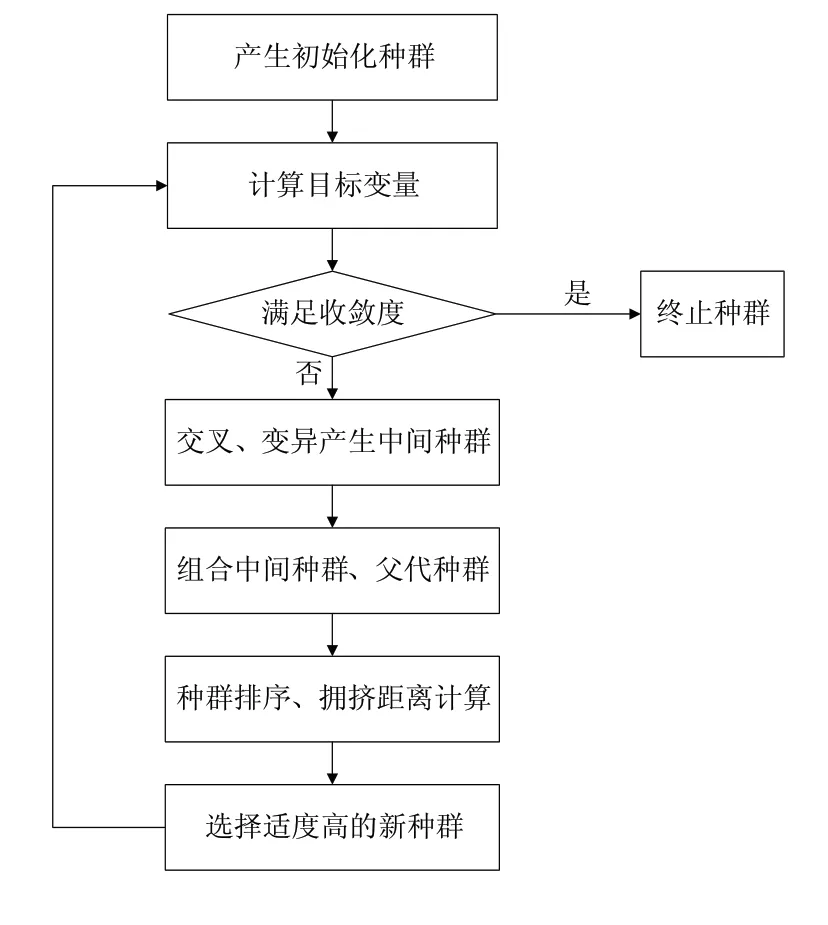
圖1 多目標遺傳算法流程圖

2 響應面方法

響應面法是構造顯示近似表達式來代替原設計問題中的約束隱式函數和目標函數，對設計點集合進行實驗設計，從而得到響應面模型來預測非試驗點的響應值。本文選用的對于n個設計變量的二階多項式響應面模型表示如下：

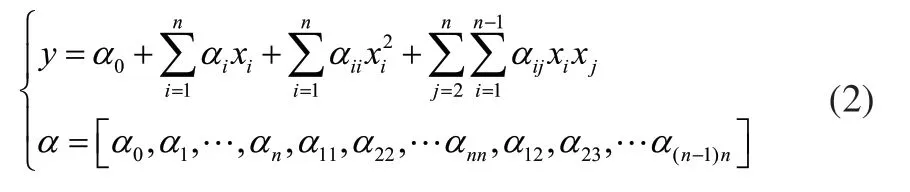
式中，為擬合函數；為設計變量；為未知系數向量，通過最小二乘法擬合得到。采用擬合優度來評價響應面模型的擬合精度，復相關系數R2是度量相關程度的指標，數值在[0，1]，越接近1，說明響應面精度越高，誤差越小[7]。

3 裝芯機排管部基座的優化設計

基于多目標遺傳算法和響應面法的裝芯機排管部基座優化設計的流程如下：根據基座的結構，確定影響優化指標的關鍵因素，利用NX 7.5建立三維參數化模型；導入至ANSYS Workbench 14.0平臺，進行靜力學分析；利用中心復合試驗確定試驗點，并重新進行有限元計算，通過試驗點和分析結果建立響應面模型；運用哈默斯利序列抽樣技術抽取樣本點，選取初始種群；最后通過多目標遺傳算法，得到最優解，實現裝芯機排管部基座的優化設計。

3.1 建立基座參數化模型

如圖2所示，排管部基座主要能夠保證鋁管順利通過槽口以及三組鏈輪上的擋塊處于同一工作平面，即要能保證滑動導軌上支撐板2、3、4處的上平面共面且變形小，即滿足一定的剛度要求。裝芯機排管部基座主要包括兩個部分：底部機身部分和左、右鋁管存放槽部分。由于安裝不同型號的芯體所需的鋁管的尺寸不同，因此需要通過導軌移動右側的鋁管存放槽部分，調節兩塊樹立大板間的距離，使其與鋁管尺寸相吻合。槽口導向板內部弧線為水平拋物線狀，可以對射出的鋁管的運動方向進行引導。

確定關鍵尺寸參數，利用NX 7.5進行基座的三維參數化建模。在關鍵尺寸參數前加前綴“DS_”便于在ANSYS Workbench 14.0中識別設計變量，并對模型簡化，建好的三維參數化模型如圖3所示。

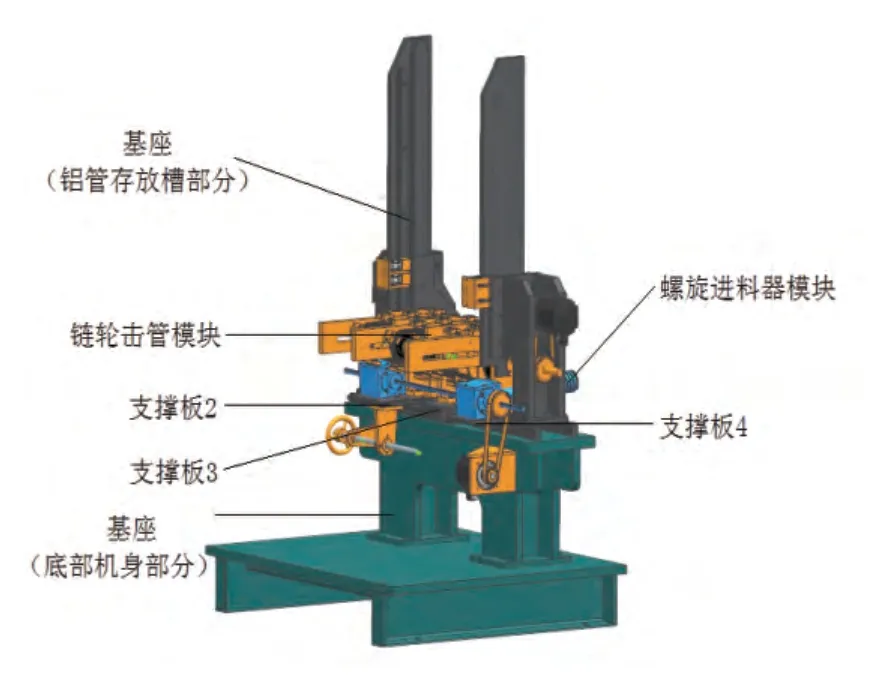
圖2 全自動汽車散熱器裝芯機排管部結構圖

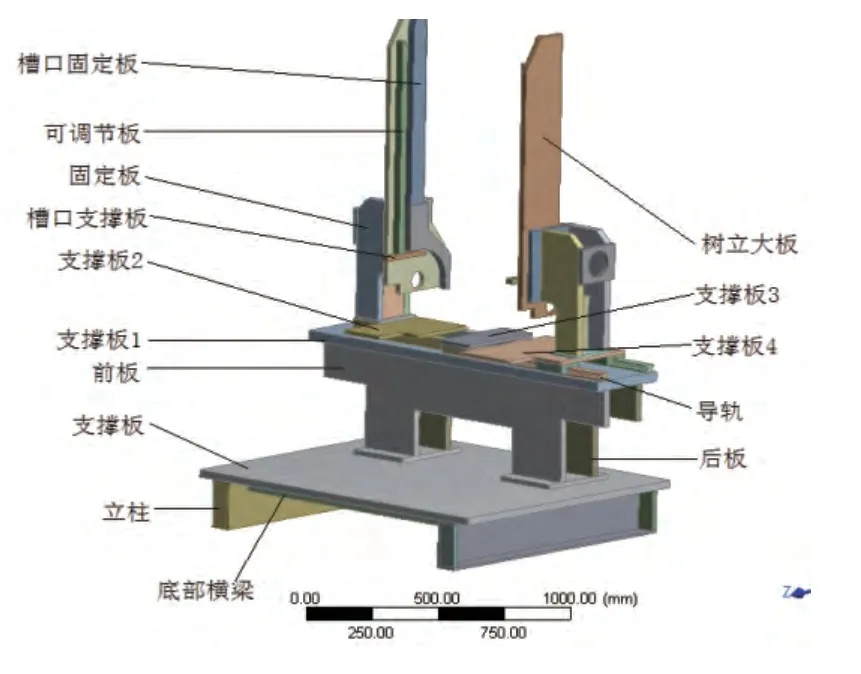
圖3 排管部基座三維參數化模型

3.2 基座有限元分析

1）有限元前處理

導入ANSYS Workbench14.0 中，進入Mechanical模塊，對基座進行靜力學分析。基座中導軌材料為HT200，密度ρ=7200kg/m3，楊氏模量E=1.48×1011Pa，泊松比λ=0.31，其余零部件材料均為45鋼，密度ρ=7890kg/m3，楊氏模量E=2.09×1011Pa，泊松比λ=0.269。導軌之間采用No Separation的接觸方式，其余零部件間采用默認的Bonded接觸方式。采用默認的網格化分，單元尺寸設置為25mm，網格劃分結果如圖4所示。

表1表示的相關變量的描述統計，可以看出居民的主觀社會地位評價平均值為4.39；接受過高等教育的樣本所占比例為17%；人際關系得分和社會態度得分的平均值分別為8.78和9.66；有房產的人數占92%；黨員的比例為12%；健康的平均值為3.67，說明大多數居民身體較為健康；性別的平均值為0.52，說明男女比例較為均衡。

圖4 基座網格劃分

整個結構依靠兩個立柱的底面支撐，故對兩個底面進行固定約束。該基座的受力情況比較復雜，但是對剛度影響較大的是如圖1中支撐板2、3、4上鏈輪擊管模塊的重力，因此重點對支撐板2、3、4進行受力分析。支撐板2、3、4上鏈輪擊管模塊的重量分別是68kg、57kg、68kg，在其上分別施加F1=680N，F2=570N，F3=680N（g=10N/kg），方向均為-Y方向。基座結構自身有重量（重量為1208.5kg），故施加標準重力9806.6mm/s2，方向為-Y方向，約束與載荷如圖5所示。

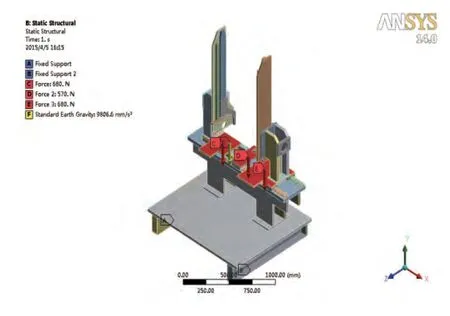
圖5 基座約束與載荷

2）有限元結果分析

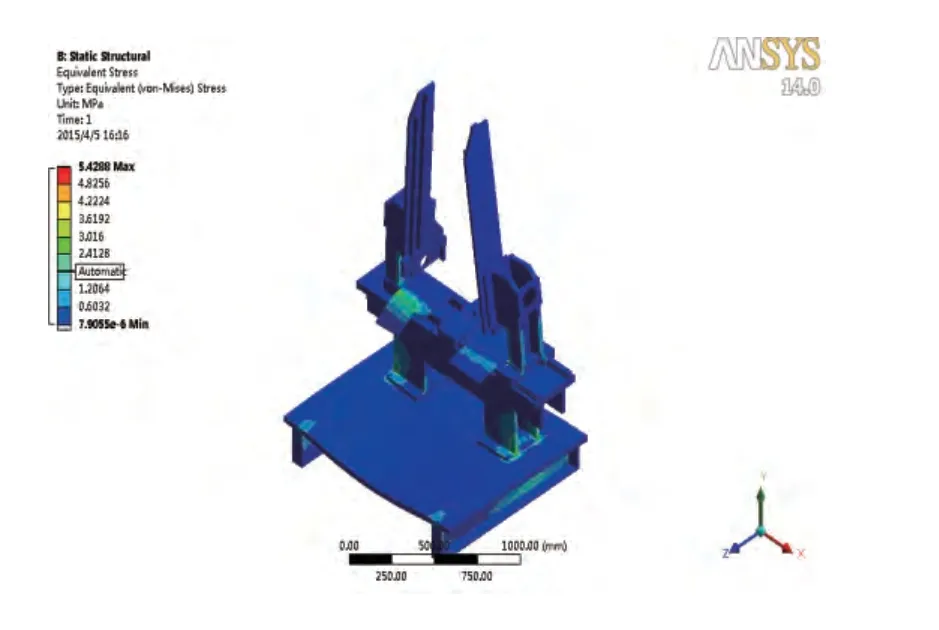
圖6 基座應力云圖

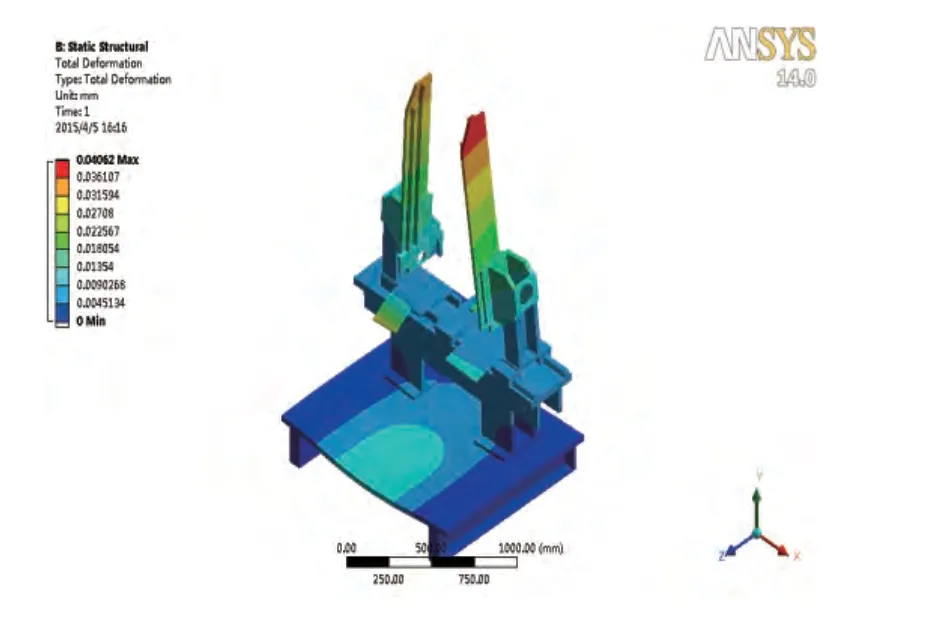
圖7 基座變形云圖

通過對基座結構的靜力學分析，得出的結果分別如圖6、圖7所示，得到以下結論：（1）基座的最大應力為5.4288MPa，遠小于材料的許用應力，在結構優化時可忽略應力的影響；（2）基座的最大變形為4.602×10-2mm，主要在樹立大板的上部以及支撐板2的前部，其余零部件變形較小，故整體結構有較大的優化空間。

3.3 基座多目標優化

1）多目標優化數學模型

以降低基座重量和提高結構剛度為雙優化目標，其中提高結構的剛度就是減小結構的最大變形量。根據公式(1)，具體的基座多目標優化設計的數學模型如式(3)所示。

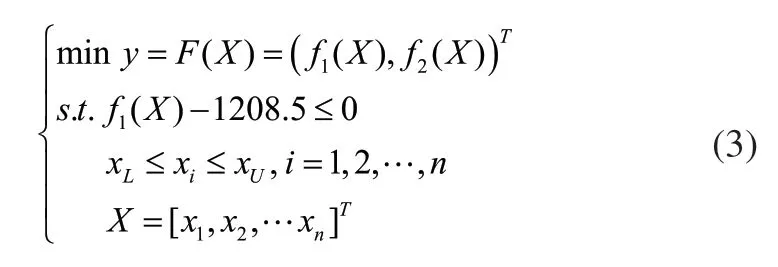
將基座結構的主要零部件尺寸作為設計變量，優化區間為初始值±10%，選取的設計變量如表1所示。

2）優化過程與結果分析

通過中心復合試驗生成了152個試驗點及有限元分析的響應結果，再利用二次插值函數生成響應面和局部靈敏度模型。通過擬合度曲線來評價響應面的擬合優度，如圖8所示，重量和最大變形量的樣本點呈一條直線趨勢，并且樣本點均在該直線附近，擬合優度較好。

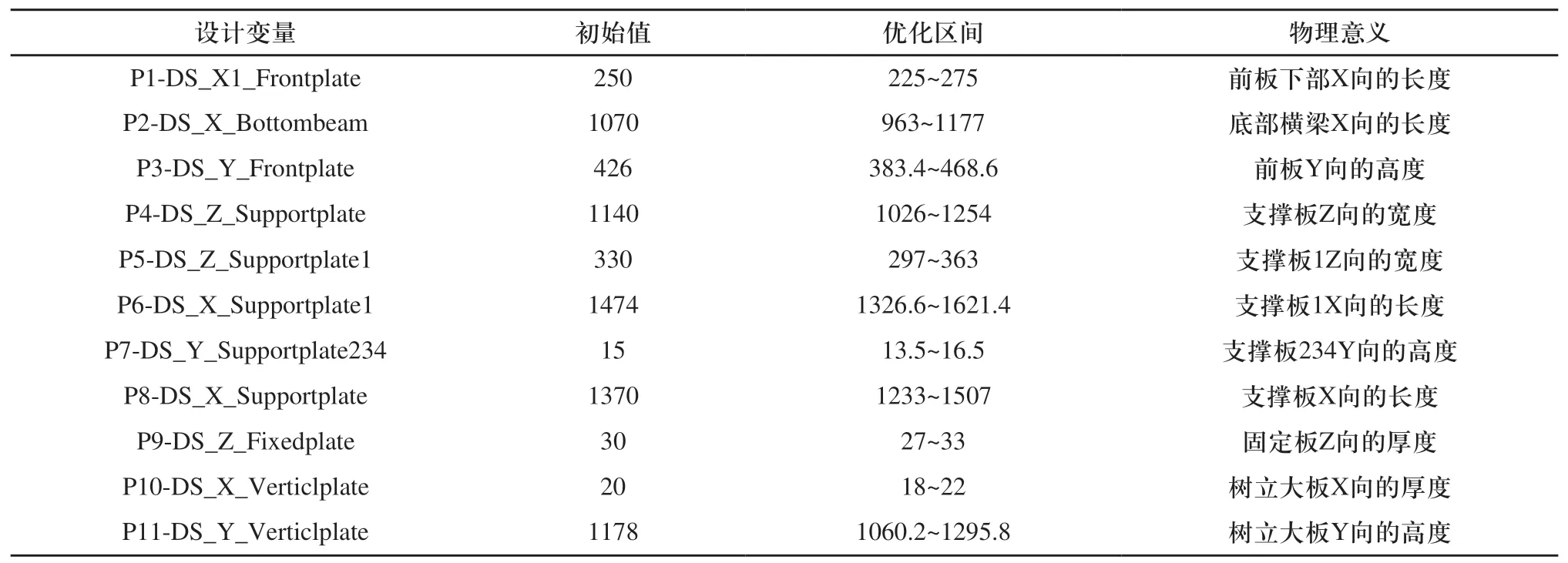
表1 基座關鍵設計變量參數（mm）

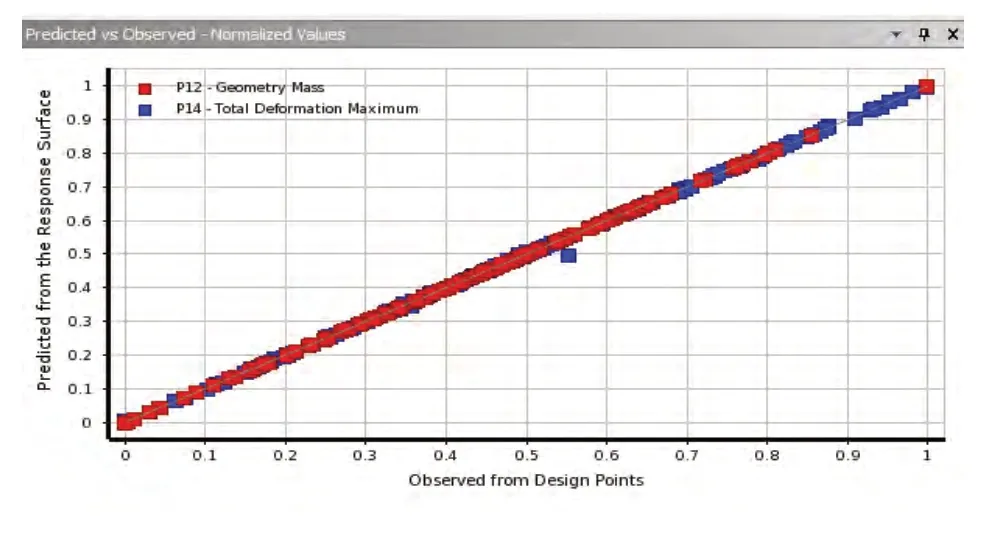
圖8 擬合度曲線

生成的局部靈敏度如圖9所示，由圖可知，對基座重量影響比較大的分別是支撐板Z向的寬度P4、支撐板X向的長度P8及前板Y向的高度；對基座剛度影響較大的分別是樹立大板Y向的高度、底部橫梁X向的長度及樹立大板X向的厚度，固定板Z向的厚度P9對結構剛度有負面影響[8]。

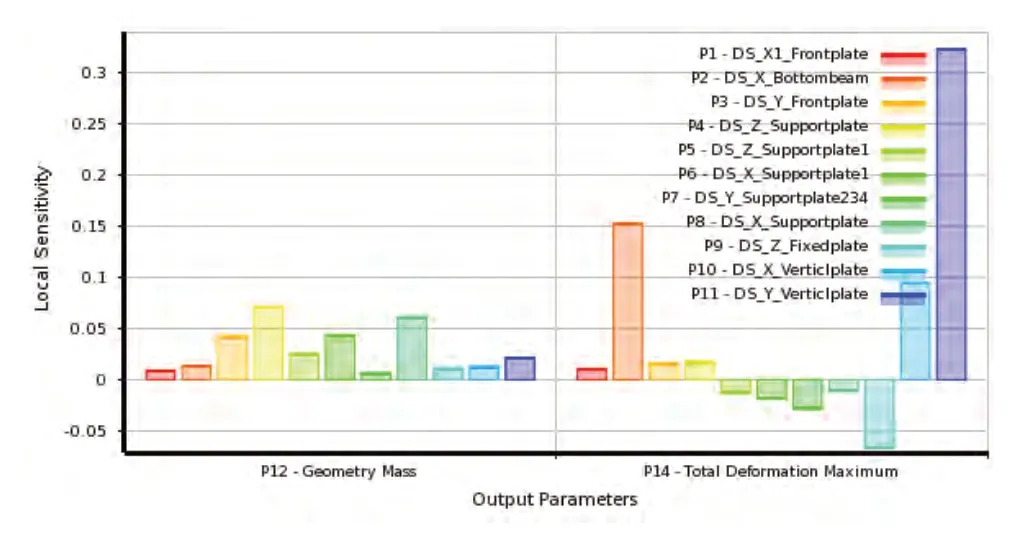
圖9 局部靈敏度

生成的響應面模型如圖10所示，由圖可知，支撐板Z向的寬度P4和X向的長度P8對基座重量影響最大，其本身變形小，結構大，最有優化的空間。

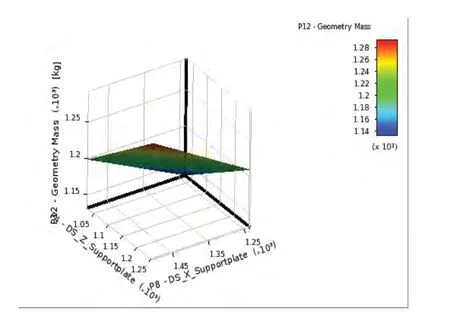
圖10 響應面

對優化目標計算求解，得到的Pareto最優解集如圖11所示。由圖可知，隨著基座重量的增加，最大變形會急劇減小；隨后最大變形取向于穩定值，不再隨著重量的增加而減小。因此，最優解位于拐點處，既能保證基座的重量小，又能保證結構的最大變形小，即基座結構的剛度大，符合多目標優化的期望。該最優解及其圓整后的數據如表2所示。

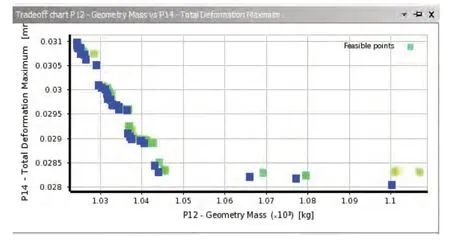
圖11 重量與最大變形的Pareto最優解集

表2 關鍵參數優化前后數據（mm）

如表3所示，基座優化圓整后的重量為1045kg，比優化前減輕13.53%；優化圓整后的最大變形為0.02974mm，比優化前減少26.78%，結構剛度有較大提高，滿足輕量化設計的要求。

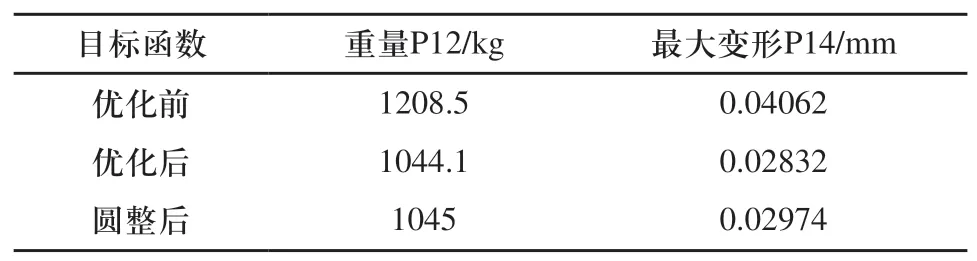
表3 優化前后結果對比

4 結論

本文是以全自動汽車散熱器裝芯機排管部基座為實例，以減輕其重量和提高其結構剛度為雙標，基于響應面模型及多目標遺傳算法的優化設計，得出結論如下：

1）優化后的結構重量比優化前減少13.53%，最大變形減少26.78%，符合輕量化設計的要求，并為以后的裝芯機及類似結構的優化提供理論依據；

2）采用多目標遺傳算法，能夠在可行域內快速、準確搜尋優化設計問題的Pareto最優解集，大大提高了多目標優化設計的效率。

[1]張清.汽車散熱器芯體全自動裝配機的設計與研究[D].安徽理工大學,2014.

[2]Fonseca C M,Fleming P J.Multi-objective Optimization and multiple constraint handling with Evolutionary algorithms-part:A unified formulation [J].IEEE Transactions on Systems,Man,and Cybernetics,Part A:Systems and Humans,1998,28(1):26-37.

[3]孫偉,張呈林.基于多目標遺傳算法的直升機總體參數優化設計[J].機械科學與技術,2010,02:265-269.

[4]顧春榮,劉德仿,周臨震,王斌,廖萍.基于多目標遺傳算法的印制電子噴印機結構輕量化設計[J].制造業自動化,2014,15:124-128.

[5]公茂果,焦李成,楊咚咚,馬文萍.進化多目標優化算法研究[J].軟件學報,2009,02:271-289.

[6]李玥.基于多目標遺傳算法的航空發動機多目標優化控制[D].南京航空航天大學,2007.

[7]趙潔.機械可靠性分析的響應面法研究[D].西北工業大學,2006.

[8]于海蓮,王永泉,陳花玲,寸花英.響應面模型與多目標遺傳算法相結合的機床立柱參數優化[J].西安交通大學學報,2012,11:80-85.