二維直方圖重建和降維的Otsu閾值分割算法

陳金位， 吳 冰

(河南理工大學電氣工程與自動化學院，河南 焦作 454150)

二維直方圖重建和降維的Otsu閾值分割算法

陳金位， 吳 冰

(河南理工大學電氣工程與自動化學院，河南 焦作 454150)

指出二維直方圖直分法中存在區域劃分不合理和抗噪性差問題，提出一種新的閾值分割方法，導出有關計算公式。首先分析噪聲點在二維直方圖中分布情況，通過重建二維直方圖減弱了噪聲對閾值分割的干擾；然后將二維直方圖區域劃分由四分法改為二分法，使得閾值搜索的空間維度從二維降到一維；最后分別給出現有二維直方圖分割算法和本文方法的仿真結果。理論分析和實驗結果表明，該方法可以運用于幾乎所有基于二維直方圖的閾值分割，特別是對受噪聲污染的圖片進行閾值分割時，能使分割后的圖片內部均勻、邊界準確、抗噪性更穩健，所需運行時間大幅減少。

圖像分割；直方圖降維；閾值選取；最大類間方差法

圖像分割是圖像處理與分析應用中一項非常重要的前期工作，國內外學者已進行了大量地研究[1-3]。目前為止，人們提出了各種各樣的圖像分割方法[4-7]，其中閾值分割法因簡單有效且易于理解而被廣泛應用。由Otsu提出的該方法是根據圖像一維灰度直方圖，采用窮舉搜索法使類間方差達到最大來確定最佳閾值[8]。1984年Reddi等針對Otsu方法，在不采用原始的窮舉搜索法，而通過假定一維灰度直方圖為連續的概率密度函數，提出了一種快速搜尋迭代法——最陡上升法[9]，該算法性能穩定且運行效率高，一般只需6～20次迭代即可收斂到最佳閾值。

1993年劉健莊和栗文青[10]將Otsu法從一維推廣到二維，結合灰度和鄰域平均灰度構成了二維直方圖，鑒于二者有很強的相關性，在一定假設下(即目標區域和背景區域上的概率和近似為1)提出了二維最大類間方差法(二維 Otsu法)。其效果較一維方法有明顯改善，因將一維信息搜索拓展為二維信息搜索，導致運算量呈指數增加，不宜處理實時問題。為此，人們提出了多種基于二維直方圖閾值選取的快速算法[11-14]，以便提高運行速度。

然而，上述二維方法及其快速算法都將二維直方圖分成四個矩形區域(區域直分)，僅考慮兩個沿對角線的矩形區域，分割結果不夠準確。郝穎明和朱楓[15]提出的快速算法雖然沒有忽略主對角線附近區域內向量點的概率分布，但仍然存在近似，忽略了部分點，抗噪穩健性不理想。針對傳統二維Otsu方法抗噪性弱、實時性差的問題，本文首先指出了二維直方圖 Otsu法存在的區域誤分，通過重建二維直方圖減弱噪聲干擾；然后通過降維來降低計算復雜度，使得閾值搜索空間維度從二維降到一維。仿真結果表明該方法較之傳統二維Otus法分割效果更好，且大大提高了運算速度。

1 二維直方圖區域直分

定義一個L×L大小的正方形區域，其橫坐標表示圖像像素的灰度級，縱坐標表示像素的鄰域平均灰度級，直方圖內任意一點的值定義為二者聯合概率密度的圖形為該圖像的二維直方圖。

目前，基于二維直方圖選取閾值的方法幾乎都采用直分法，即利用閾值向量(s,t)，采用分別與灰度級、鄰域平均灰度級兩坐標軸平行的互相垂直的十字線，將二維直方圖分割成如圖1所示的4個矩形區域。

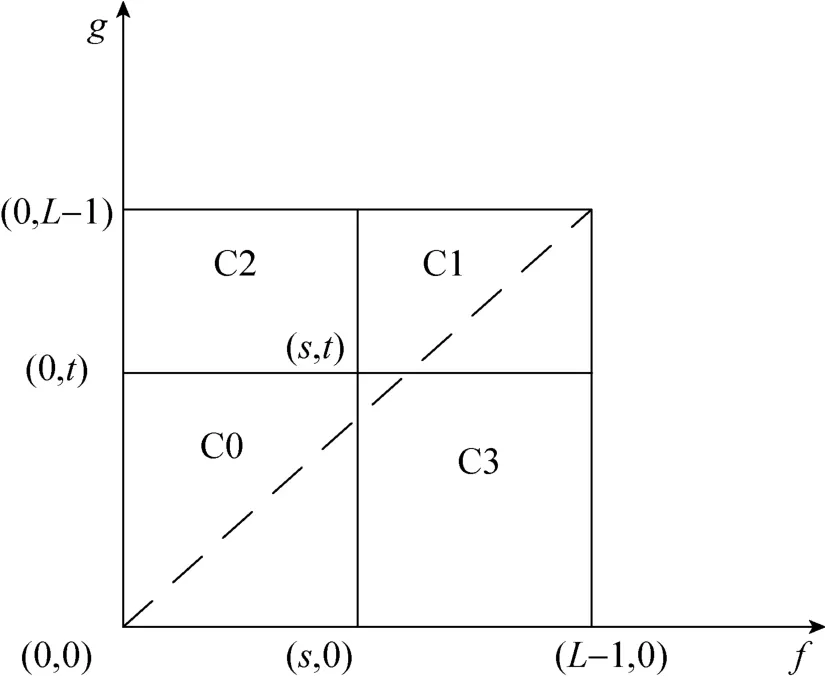
圖1 二維直方圖直分法

圖1中4個區域分別用C0、C1、C2和C3表示，假設圖像的暗(亮)像素屬于目標(背景)，則區域C0和目標對應，區域C1和背景對應，區域C2和C3則表示邊緣和噪聲，計算時僅考慮區域C0和C1內的概率，而假設區域C2和C3內的概率和近似為零。最后通過Otsu準則獲取最佳閾值點。

2 二維直方圖重建和降維

2.1 二維直方圖直分法存在的不足

(1) 對區域C2和C3的忽略不計與實際不符。因大部分邊緣像素點和噪聲點分布在遠離對角線的區域，所以對C2和C3區域的忽略不計直接導致大量邊緣信息丟失。盡管該區域內像素點數遠少于背景和目標區域內的像素點數，但仍會影響對圖像的分割準度。

(2) 對噪聲的處理不統一，抗噪性能弱。雖然忽略了區域C2和C3內的噪聲，但區域C0和C1中仍可能存在大量噪聲，二維直分法并沒有對其進行處理。尤其當圖片受噪聲干擾后，噪聲點的分布隨機性較大，導致目標區域內的噪聲點分布于二維直方圖中的背景區域內，而處于背景區域內的噪聲點則分布在二維直方圖中的目標區域內，這種分布的隨機性隨著噪聲干擾程度的增強而加大，直接造成二維直方圖的分布與正常分布存在較大偏差，影響處理結果。另外，在獲取最佳閾值后，二值化圖像是對整個區域(包括 C2和C3)進行分割，由于噪聲分布的隨機性，致使二值

化后的圖像中出現了“黑點”或“白點”現象。也就是說，目標區域內的一些噪聲點被誤認為是背景，二值化成背景點，導致在黑色目標區域中形成“白點”；同樣，背景區域內分布的一些噪聲點被誤認為是目標，將其二值化成目標點，導致在白色背景區域中形成“黑點”。

可以看出，二維Otsu法考慮了空間鄰域均值信息，但并未從根本上達到去噪目的。在實際應用中，如果圖像受噪聲影響小且背景和目標像素變化均勻時，該方法尚能達到預期分割效果，但當圖像受噪聲影響較大時，用該方法得到的分割效果就不夠理想，所以有必要對二維直方圖中的一些信息點進行矯正，即二維直方圖重建，使其分布盡量恢復到正常狀態，以減弱噪聲對閾值分割的影響。

(3) 時間和空間復雜度較大。由于該方法在求得最佳閾值時，遍歷了整個二維空間，使得計算時間較長，無法滿足實時性要求，加之其所需存儲空間較大，在實際項目中很難得到應用，對其進行改進勢在必然。

2.2 二維直方圖重建

由上述分析可知，傳統的二維直方圖直分法存在錯分情況，特別當圖片受噪聲污染嚴重時，其缺點更加明顯，不能滿足分割要求。為此，本文將二維直方圖重建，做兩條平行直方圖主對角線的直線f=g+n和f=g–n分別交坐標軸于點(n,0)和(0,n)，過閾值點(s,t)做直線T=f+g垂直于主對角線。將原直方圖的4個區域劃分成如圖2所示的14個區域。

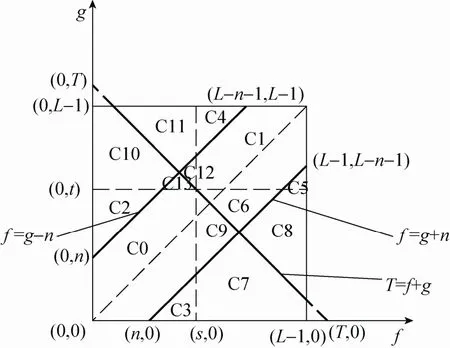
圖2 二維直方圖重建

對重新劃分的區域進行分析：

(1) C0區域。這個區域中的灰度值和鄰域平均灰度值都較小，分布在主對角線附近，二者大小十分接近，為圖像的目標區。

(2) C1區域。這個區域中的灰度值和鄰域平均灰度值都較大，分布在主對角線附近，二者大小十分接近，為圖像的背景區。

(3) (C2、C10、C11、C4)區域。這4個區域內像素的鄰域平均灰度值遠大于該像素的灰度值，為背景區域內的噪聲。

(4) (C3、C7、C8、C5)區域。這4個區域內像素的鄰域平均灰度值遠小于該像素的灰度值，為目標區域內的噪聲。

(5) (C13、C9)區域。此區域因像素點灰度級和鄰域平均灰度級有一定差別，視為目標和背景之間過渡的邊界點且是靠近目標區域部分的邊緣像素點。

(6) (C12、C6)區域。此區域因像素點灰度級和鄰域平均灰度級有一定差別，視為目標和背景之間過渡的邊界點且是靠近背景區域部分的邊緣像素點。

通過上述分析，其矯正方法如下：

對于情況(1)和(2)，屬于正常分布，不需要矯正。對于情況(3)，據分析可知，該區域內的點為背景區域內的噪聲點，需要矯正，令f*(x,y)=g(x,y)，f*(x,y)為矯正后的像素灰度值。同理，對于情況(4)，該區域內的點為目標區域內的噪聲點，需要矯正，令f*(x,y)=g(x,y)。由圖2可知被矯正區域的大小與兩條直線f=g-n和f=g+n的選取有關，兩直線與兩坐標軸的交點都為n，對于圖像受噪聲影響情況的不同，合理地選取 n值，能較理想地重建二維直方圖。

二維直方圖重建將直方圖內邊界點區和噪聲點區進一步劃分成對應于目標和背景的兩個子區。上述討論的都是 L-1＜T≤2L-2的情況，而0≤T≤L-1的情況類似，在此不再贅述。

對于正常分布的非噪聲像素點可能也會滿足(3)和(4)中某種情況，但因其灰度值和均值十分接近，故使用上述矯正方法矯正后，其分布基本不受影響。

2.3 降維的Otsu閾值分割法

斜線 T=f+g將二維直方圖分成兩類，表示目標和背景。

(1) 當0≤T≤L-1時，斜線左下角部分對應目標，可以從(0,0)點開始逐點累加算出目標的概率W0(T)及u0i(T)與u0j(T)：

(2) 當L-1＜T≤2L-2時，斜線右上三角部分對應背景，從(L-1,L-1)點開始逐點累加，先求出背景的概率W1(T)及u1i(T)與u1j(T)：

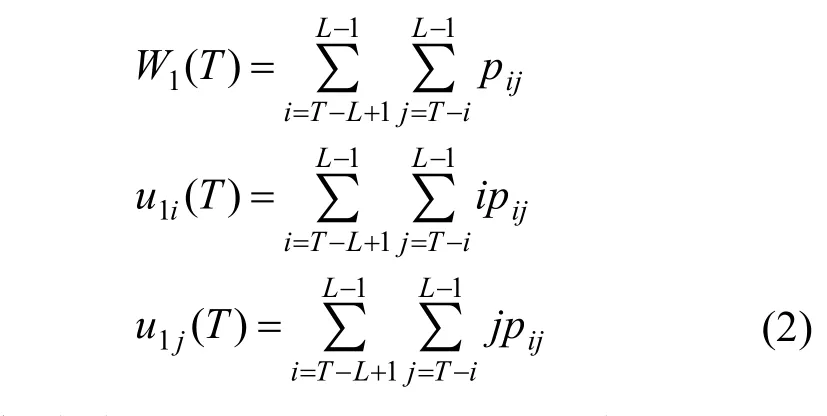
因斜線將直方圖分成的兩部分包含了直方圖內所有信息點，所以容易得到：

將其推導后得：

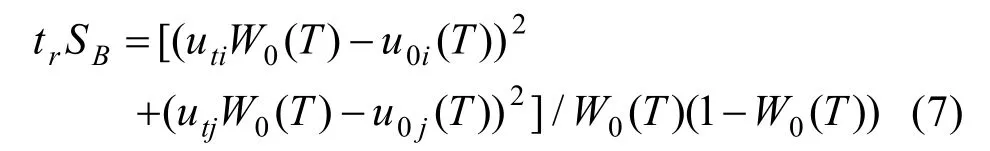
選擇測度函數SB的跡的最大值作為二維最大類間方差門限法的最佳門限向量(T0)：

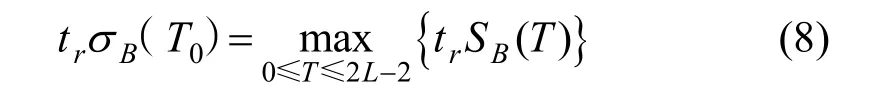
從上述分析可知，每次計算類間離散度 trSB都需從i=0，j=0開始累加計算，且T的取值越接近 L-1， trSB的計算時間越長，為了提高運算速度，可采用以下遞推公式。

當0≤T≤L-1時：

當L-1＜T≤2L-2時可推出：

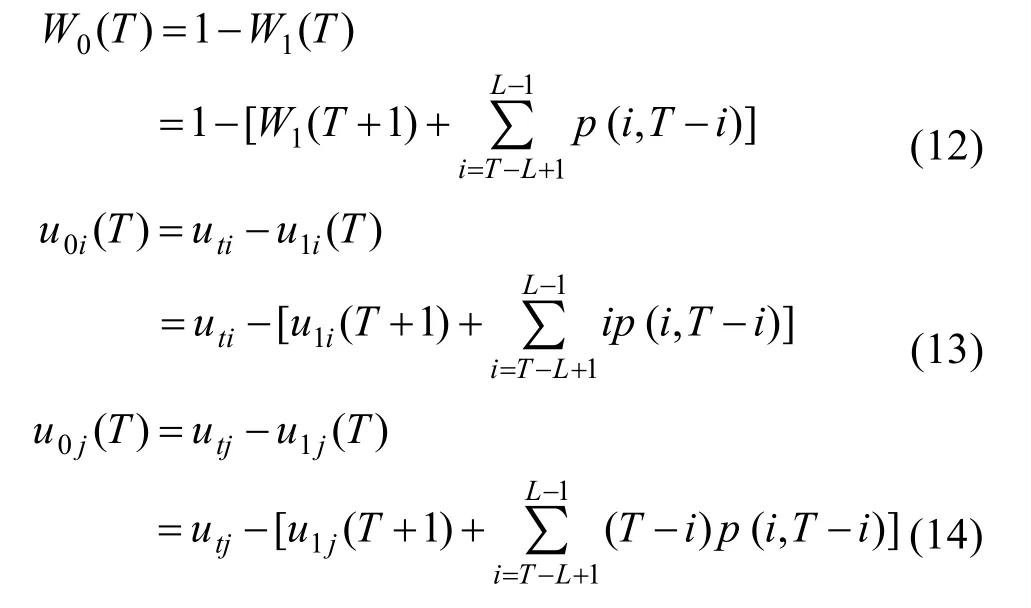
由上式可知，每次計算 trSB時，只要分別利用前面得到的和再加上直線T=f+g上各點對應的值即可。這樣將計算的復雜度從O(L3) 降到O(L)，大大提高了運算效率。

3 實驗結果與分析

本實驗是在Intel(R) Core(TM) i5-3230M CPU 2.6 GHz、內存為4.00 G(3.82 GB可用)、64位操作系統下運行的，編程環境為MATLAB R2013(b)。其對大量的圖片進行了仿真，并將仿真結果與若干種方法對比，發現本文算法分割結果準確，抗噪性相當穩健，取經典圖像moon.tif(255×255)、spin.tif(490×367)和coins.png(300×240)作為實驗目標，與文獻[10]算法及文獻[11]算法的圖像處理效果和運行時間進行比較。圖3為原始圖像，圖4～6為加入服從N(0,0.2)分布的隨機噪聲后處理的結果，表1為其仿真閾值和所需時間對比表。

圖3 無噪moon.tif分割結果

圖4 含噪moon.tif分割結果

圖5 含噪spin.tif圖片的分割結果

圖6 含噪coins.png分割結果

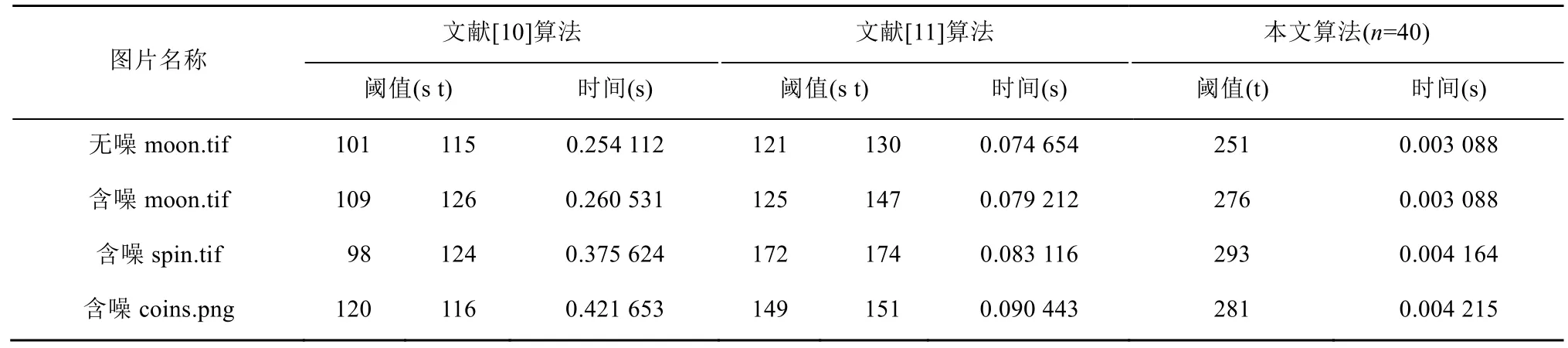
表1 算法的分割閾值及運行時間

圖3中無噪moon.tif圖片在文獻[10]、文獻[11]和本文算法下的仿真結果相似，這是因為無噪時圖像背景與目標變化均勻，大部分像素點的灰度值與鄰域平均灰度相近，分布在直方圖主對角線附近，二維灰度直方圖C2、C10、C11、C4、C3、C7、C5、C8區域內的分布概率較小。

圖 4～6為含噪圖片，本文的分割效果比文獻[10]、文獻[11]更好，抗噪性更穩健，在取不同 n值時發現，當含噪圖片在n=40以后，分割閾值幾乎不隨n的增大而變化，因此將n=40時的閾值作為最佳閾值。文獻[10]中的快速算法雖然在時間上比傳統分割算法有很大提高且錯分的噪聲點區域比原始直分算法少，但是忽略了遠離對角線的兩個區域內的噪聲點，通常表現為像素點較少，當對圖像處理結果要求較高時，效果不很理想。表1可見，本文將閾值搜索空間維度從二維降到一維，運用給出的遞推算法比文獻[11]的運行時間少了一個數量級，比文獻[10]少了約兩個數量級。根據圖像含噪的不同程度，合理選取 n值，可獲得最佳分割閾值。

4 結 論

本文提出的二維直方圖重建及降維的Otsu算法有兩個明顯優勢：其一，當圖片受噪聲污染時，根據選定的 n值將圖片的像素灰度值矯正，重建二維直方圖，從而使分割后圖像區域內部更均勻，抗噪性更穩健；其二，用斜分法代替傳統二維Otsu法中的窮舉搜索法，把計算的復雜度從二維降到一維，計算速度可大大提高。本文算法使基于二維直方圖的閾值分割方法在工程中更為實用。

[1] 吳一全, 朱兆達. 圖像處理中閾值選取方法30年(1962－1992)的進展(一)[J]. 數據采集與處理, 1993, 8(3)： 193-201.

[2] 吳一全, 朱兆達. 圖像處理中閾值選取方法30年(1962－1992)的進展(二)[J]. 數據采集與處理, 1993, 8(4)： 268-282.

[3] Reddi S S, Rudin S F, Keshavan H R. An optimal multiple threshold scheme for image segmentation [J]. IEEE Transactions on Systems, Man, and Cybernetics, 1984, 14(4)： 661-665.

[4] 陳 果. 圖像閾值分割的Fisher準則函數法[J]. 儀器儀表學報, 2003, 24(6)： 564-567.

[5] 朱曉臨, 鄧祥龍, 胡德敏. 多閾值選取與邊緣連接的邊緣檢測算法[J]. 圖學學報, 2012, 33(2)： 72-76.

[6] Sahoo P K, Soltani S, Wong A K C, et al. A survey of thresholding techniques [J]. Computer Vision, Graphics and Image Processing, 1988, 41： 233-260.

[7] 龔軍輝, 陳愛萍, 唐勇奇, 等. 一種快速有效的虹膜圖像預處理方法[J]. 圖學學報, 2012, 33(4)： 93-97.

[8] Nikhil R P, Sankar K P. A review on image segmentation techniques [J]. Pattern Recognition, 1993, 26(9)： 1277-1294.

[9] Nobuyuki O. A threshold selection method from gray-level histograms [J]. IEEE Transactions on Systems, Man, and Cybernetics, 1979, 9(1)： 62-66.

[10] 劉健莊, 粟文青. 灰度圖像的二維 Otsu自動閾值分割法[J]. 自動化學報, 1993, 19(1)： 101-105.

[11] Gong Jian, Li Liyuan, Chen Weinan. A fast recursive algorithm for two-dimensional thresholding [J]. Signal Processing, 1996, 2： 1155-1158.

[12] 景曉軍, 蔡安妮, 孫景鰲. 一種基于二維最大類間方差的圖像分割算法[J]. 通信學報, 2001, 22(4)： 71-76.

[13] 汪海洋, 潘德爐, 夏德深. 二維Otsu自適應閾值選取算法的快速實現[J]. 自動化學報, 2007, 33(9)：968-971.

[14] 吳一全, 潘 喆. 2維最大類間平均離差閾值選取快速遞推算法[J]. 中國圖象圖形學報, 2009, 14(3)：471-476.

[15] 郝穎明, 朱 楓. 2維Otsu自適應閾值的快速算法[J].中國圖象圖形學報, 2005, 10(4)： 484-488.

A Otsu Threshold Segmentation Method Based on Rebuilding and Dimension Reduction of the Two-Dimensional Histogram

Chen Jinwei, Wu Bing
(School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo Henan 454150, China)

The issue of poor resistance to noise and unreasonable is pointed out based on two-dimensional histogram regional straight points method. A new threshold segmentation method is proposed, and the calculation formula of the method is deduced. Firstly, in this method, noise interference weakened for threshold′s segmentation through the reconstruction of two-dimensional histogram based on detailed analysis of noise distribution in the two-dimensional histogram, and then, the region division is transfered from eight partitions into two partitions in two-dimensional histogram. Thus the two-dimension search space of threshold is reduced to one-dimension. Finally, simulation results of existing two-dimensional histogram segmentation algorithm and our method are given respectively. Theoretical analysis and experimental results show that our method could be used in nearly all the two-dimensional histogram threshold segmentation, especially in threshold segmentation with the contaminated image. It makes the inner part uniform, the edge accurate in the threshold image and has better tolerance capability to noise. The running time is significantly reduced.

image segmentation; histogram dimensionality reduction; threshold selection; Otsu algorithm

TP 317.4

A

2095-302X(2015)04-0570-06

2014-08-27；定稿日期：2014-12-19

陳金位(1990–)，男，河南安陽人，碩士研究生。主要研究方向為圖像處理。E-mail：chenjwhpu@163.com

吳 冰(1964–)，男，江西萍鄉人，教授，博士。主要研究方向為通信與信息系統研究。E-mail：wubing@hpu.edu.cn