聯系數的一種新的取值方法及其應用

梅曉玲，謝承榮 （鄖陽師范高等專科學校數學與財經系，湖北 十堰442000）

保加利亞學者K.T.Atanassov在1999年將僅考慮隸屬度的Zadeh模糊集［1］推廣到同時考慮隸屬度、非隸屬度和猶豫度3個方面，提出了直覺模糊集［2］的概念。相比模糊集，直覺模糊集更能形象描述與刻畫現實生活中的許多不確定性問題，受到學者們的關注和重視，并取得了不少研究成果。但如何深刻地認識模糊不確定性的本質，并且客觀地用適當的數學工具來研究模糊問題中的不確定性是要深入研究的課題。聯系數［3］可用于處理模糊、隨機、中介和信息不完全所致不確定性問題，聯系數理論為研究模糊問題中的不確定性提供新的思路。以聯系數為工具研究直覺模糊集的關鍵是聯系數中i的取值問題，筆者在已有的i的取值方法基礎上，利用IF點算子提出新的i的取值方法。

1 聯系數的概念

聯系數是把給定范圍內確定性和不確定性聯系起來的一種數，其把不確定性與確定性作為一個整體，系統地進行數學處理和辨證分析。聯系數的定義式為：

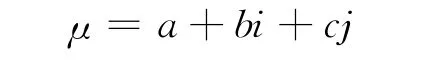
在聯系數μ的定義式中，i和j有雙重意義［4，5］。

第1個含義是稱j為對立系數。j在計算時、取j＝－1；i稱為差異系數，i∈［－1，1］且是不確定取值。a稱為同一數（同一度），b稱為差異數（差異度），c稱為對立數（對立度），分別是關于所研究的對象系統的同一性測度、差異性測度和對立性測度。聯系數的意義在于把研究對象的同一性測度（同一數）、差異性測度（差異數）和對立性測度（對立數）聯系在一起，組成一個同異反系統。在聯系數意義下，不僅在宏觀上有a＋b＋c＝1這一約束，而且由于j＝－1，i∈［－1，1］同時又刻劃出a，b，c在微觀層次上的互相聯系，互相滲透，因而具有豐富的系統信息。第2個含義是不計較i和j的取值情況，此時僅起標記的作用。關于聯系數的運算法則，這里只列舉筆者研究所需要的加法、數乘運算及大小比較［4］。

1）加法運算：

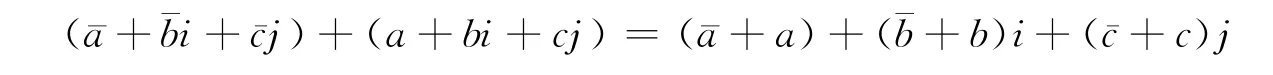
2）常數與聯系數的乘積：

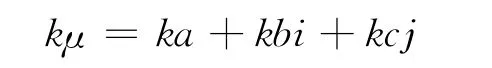
3）大小比較方法。設u1＝a1＋b1i＋c1j，u2＝a2＋b2i＋c2j，則：

若i∈I?［－1，1］時，u1－u2＞0，則在i∈I這個范圍內有u1＞u2。同理，u1－u2＜0時，u1＜u2。

2 聯系數與直覺模糊數的關系

聯系數與直覺模糊數關系密切，在概念、組織形式、應用上有所不同，但在研究刻畫不確定系統時有著異曲同工之妙［6］。

聯系數μ＝a＋bi＋cj（a＋b＋c＝1），只考慮了離散型且為有限的情況，現在將其推廣到一般的離散與連續情形。

對于i∈［－1，1］，i＝－1，i、j僅起標記作用時可以用類似于“內積”的運算求得μ，即：

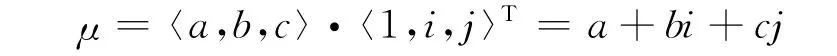
用閉區間［0，1］上的2個函數μA（x），νA（x）分別表示論域X上的任意元素x對問題A的支持和反對的證據，即為聯系數表達式中的同一度與對立度，且滿足μA（x）＋νA（x）≤1；函數 πA（x）＝1－μA（x）－μA（x）為元素x支持A與否的不確定程度，現為聯系數表達式中的差異度，由此聯系數與直覺模糊數結合起來，表達式可改寫為：

其中，μA（x）＋πA（x）＋νA（x）＝1，πA（x）可以由μA（x），νA（x）確定，即由同一度和對立度來確定差異度（不確定度）。

用表達式μ（A）＝μA（x）＋πA（x）i＋νA（x）j來表達元素x符合A的隸屬程度，將聯系數和直覺模糊數進一步結合，結合的過程可以說明聯系數是直覺模糊（IFS）理論的擴展，而直覺模糊（IFS）是聯系數的又一種形式。

3 聯系數新的取值方法

聯系數表達式μ（A）＝a＋bi＋cj辨證且系統地描述了不確定性，表達式中不確定項bi的給出是關鍵之處，在一定的條件下用其來對“棄權”這種不確定性進行分解，這里i的取值將棄權中的同一與對立分離出來，定量分析其中的贊同、反對的程度。

直覺模糊集中的猶豫指數πA（x）＝1－μA（x）－νA（x）為x支持A與否的不確定程度，也為聯系數表達式中的差異度。直覺模糊集的3個構成指標用投票模型來解釋即為贊成、反對和棄權，這里棄權所造成的不確定性對決策的結果會產生直接影響，所以考慮將棄權部分的信息盡可能準確化，由此思考利用IF點算子［7］對“棄權”問題進行深度挖掘與剖析，提高決策的準確性，降低模糊指標的不確定性對決策帶來的影響。

將一直覺模糊集A轉化為帶有如下直覺指數：

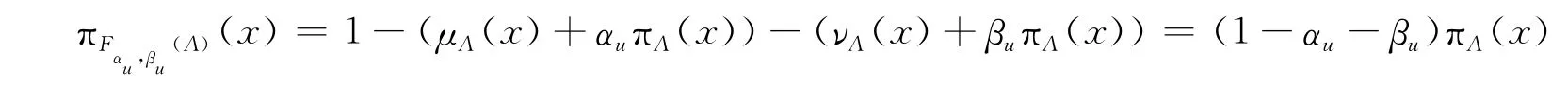
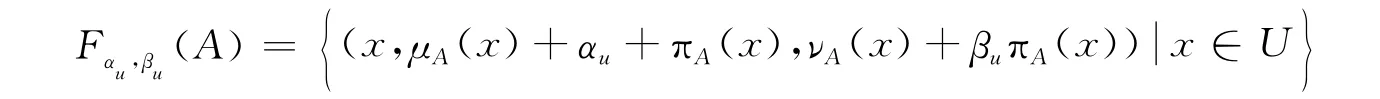
從而得到新的贊成、反對和棄權票的比例分別為μA（x）＋αuπA（x），νA（x）＋βuπA（x）和（1－αu－βu）πA（x）。這里，對任意A∈IFS（U），αu，βu∈ ［0，1］，且αu＋βu＜1。

顯然對任意x∈U，有≤πA（x），對A∈IFS（U），若記：

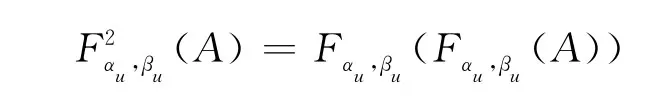
則：

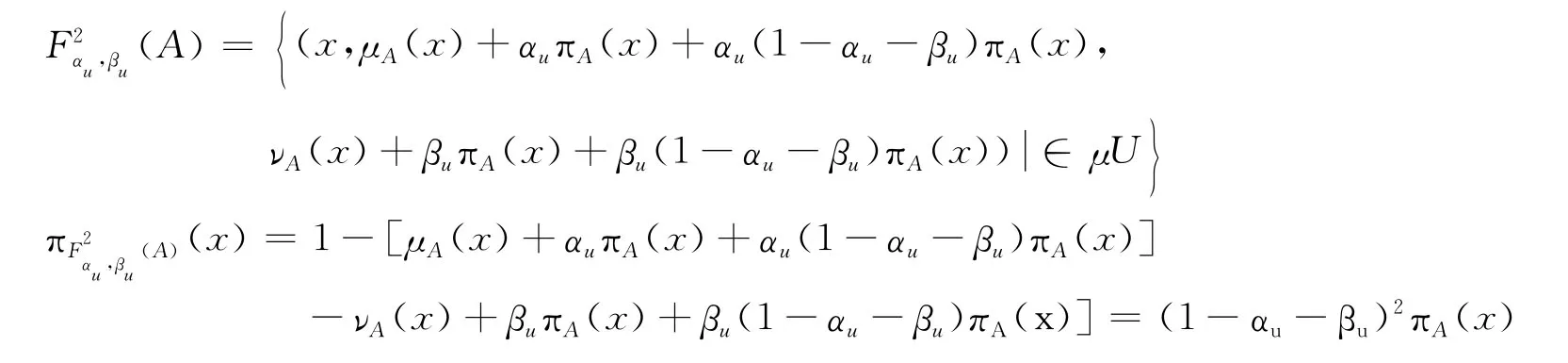
進一步有：

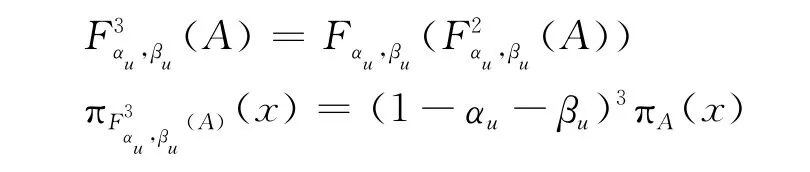
推廣到一般情形，對任意正整數n有：

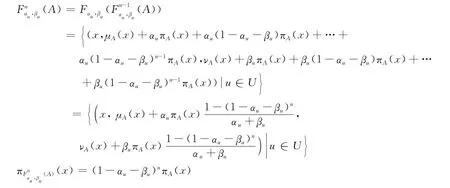
由上面的分析可以得到聯系數表達式中i的取值方法：

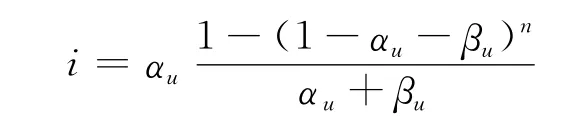
則得到新的聯系數取值方法，即：

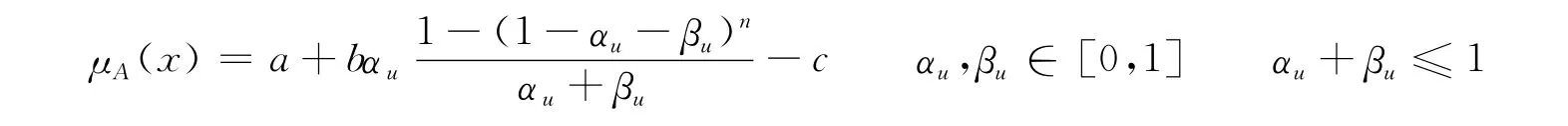
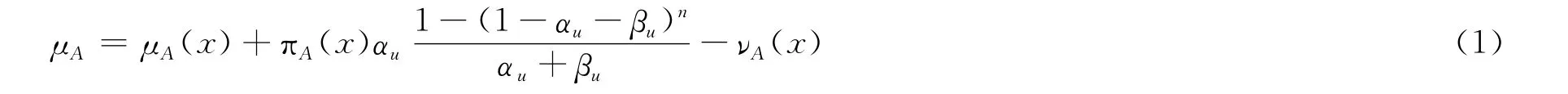
這里得到的新的i的取值方法中，若取n＝1，αu＝μA（u），βu＝νA（u）時，取值結果與順勢取值法［7］相同。

一般地取：

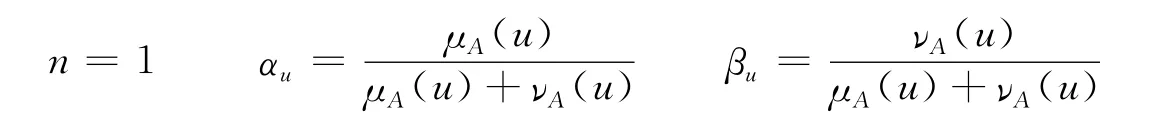
也即x符合A的隸屬程度：

4 實例分析

例1（空調系統選擇問題［8］） 假設有3種空調系統（方案）a1、a2、a3，在選擇過程中需要考慮3種屬性：u1代表經濟屬性，u2代表功能，u3代表有效性。已知決策矩陣如表1所示，屬性權重為w1＝0.4751，w2＝0.2786，w3＝0.2463。

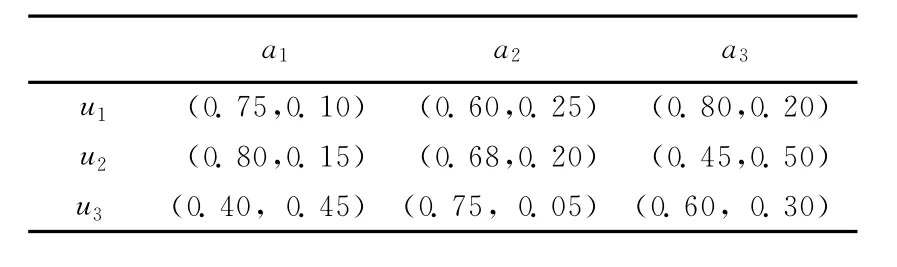
表1 決策矩陣～X

由聯系數的概念，利用筆者提出的i的取值方法取：

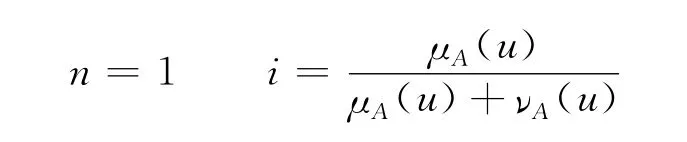
將各方案的直覺模糊屬性值由式（1）轉化為聯系數值，然后將得到的各屬性聯系數值加權求和：

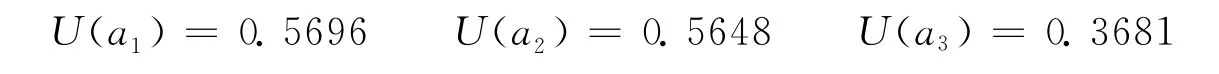
由聯系數的大小方法可知方案的排序為：

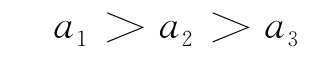
該結果與文獻［6］的結果相同，但比較這2種方法的計算過程，筆者提出的方法大大簡化了計算過程，減小了計算量，快速準確。

5 結語

以聯系數為工具研究不確定性問題的關鍵是聯系數中i的取值問題，筆者提出的聯系數的取值方法對直覺模糊集的猶豫度（不確定性）進行了更準確、更細致的挖掘，不確定性問題的準確性得到進一步提高。但如何深刻地認識模糊不確定性的本質，對不同類型的不確定性問題選擇合適的數學工具進行精確與量化需要更進一步的深入研究。

［1］Zadeh L A.Fuzzy sets［J］.Inform and Control，1965，8（3）：338～353.

［2］Atanassov K T.Intuitionistic fuzzy sets ［J］.Fuzzy Sets and Systems，1986，20：87～96.

［3］趙克勤 .集對分析及其應用 ［M］.杭州：浙江科學技術出版社，1992：68～80.

［4］趙克勤 .聯系數及其應用 ［J］.吉林師范學院學報，1996，17（8）：50～53.

［5］王堅強 .幾類信息不完全確定的多準則決策方法研究 ［J］.長沙：中南大學，2005.

［6］Deschrijver G，Kerre E.on the relationship between some extensions of fuzzy set theory ［J］.Fuzzy Sets and Systems，2003，133：227～235.

［7］Li Dengfeng.Multiattribute decision making models and methods using intuitionistic fuzzy sets ［J］.Journal of Computer and System Sciences，2004，70（1）：73～85.

［8］徐澤水 .不確定多屬性決策方法及應用 ［M］.北京：清華大學出版社，2004：58～63.