一種高效的基于初始聚類中心優化的K-means算法

張曉倩，曲福恒，楊勇，才華，梁鮮

（長春理工大學 計算機科學技術學院，長春 130022）

聚類分析是數據挖掘中常用的無監督學習方法［1］。聚類問題的基本形式被定義為找到給定數據集中的同組數據，每組數據又稱為一個簇，并且處于某個簇中的數據對象的密度高于該對象處于其它的簇。目前已有的聚類方法很多，根據基本聚類思想的不同，聚類分析方法大致可以分為劃分聚類、層次聚類、密度聚類、網格聚類和模型聚類五大類。

聚類分析旨在將給定的數據集劃分為不相干的子集，并且每個子集中的數據對象具有較高的相似度。K-means是一種最常用的迭代劃分聚類算法，使用該算法進行聚類時，首先它需要指定集群的數量，然后，提供初始數據集的劃分并且這些初始簇的質心是提前計算出來的。在最初的K-means方法中，初始集群通常是隨機選擇的，顯然，這種隨機性會導致聚類結果的不穩定。為解決這個問題，許多K-means的初始化方法被提出。如文獻［2］提出基于相異度的K-means改進算法，根據由相異度矩陣組成的霍夫曼樹選擇初始質心。文獻［3］提出了一種利用反向最近鄰（RNN）搜索方法選取初始質心。文獻［4］結合數據密度分布和kd-tree進行選擇初始質心。文獻［5］根據樣本空間分布信息，根據每個數據樣本方差的大小以及樣本間平均距離選取初始聚類中心。文獻［6］提出了基于全局優化的思想選取初始聚類中心，該算法通過多次運行K-means算法得到k個初始聚類中心。但由于選取初始質心的計算代價和時間代價大，該文獻中又提出了快速全局K-means聚類算法，對選取初始中心的方法進行了改進，縮短了聚類時間。本文在文獻［7］提出算法的基礎上，對進一步提高聚類算法的效率問題進行了研究，提出了一種高效的基于初始聚類中心優化的K-means算法，通過存儲每次迭代中的一些信息，用于下一次迭代，減少一部分計算量，提高算法執行效率。

1 最小方差優化初始聚類中心的K-均值算法

傳統的K-means算法的聚類過程是隨機選擇k個初始質心，根據最近鄰原則，將數據集中的數據樣本與最近的初始質心歸為一類，重復迭代，直至初始質心不再發生變化或準則函數收斂，得到最終的k個簇。K-means算法的核心計算為計算每個數據對象到k個聚類中心的距離，算法的時間復雜度為O（nkt），其中，n為數據對象個數，t為迭代次數。

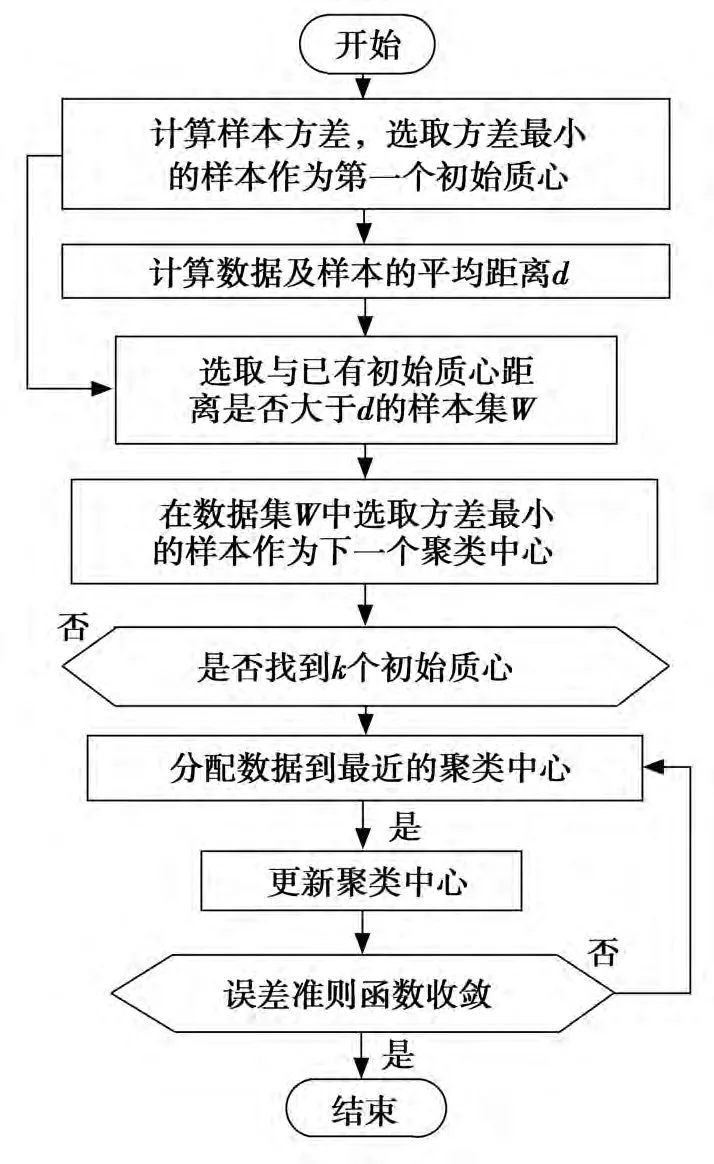
圖1 最小方差K均值算法流程圖

最小方差優化初始聚類中心的K-means算法［6］根據樣本空間分布信息，根據每個數據樣本方差的大小以及樣本間平均距離選取初始聚類中心。首先選擇所有樣本中方差最小的那個作為第一個初始聚類中心；然后選取距離第一初始聚類中心距離大于樣本間平均距離并且方差最小的樣本作為第二個初始中心；重復該過程，直到找到k個初始聚類中心。在選取k個初始質心時，首先計算樣本之間的距離矩陣，然后根據距離矩陣中的數據計算每個數據樣本方差的大小，總的時間復雜度為O（n2），其中選取初始質心的時間復雜度為O（n2），在對每個數據對象進行歸類分配時的時間復雜度為O（nkt1），其中t1為迭代次數。算法流程如圖1所示。

2 本文改進算法

在K-means算法聚類過程中，在每次迭代數據點分配的過程中，需要每個計算數據點到所有聚類中心的距離，而在不斷迭代過程中，一些樣本點所在簇是不發生變化的。文獻［7］中提出了一種改進的K-means算法，通過設置簡單的數據結構，存儲每次迭代中的一些信息用于下一次迭代。主要思想是：設置兩個簡單的數據結構，保存所有數據點的簇標志和到最近中心點的距離，用于下一次迭代，在計算數據對象到新中心的距離，如果這個距離小于或等于到原來中心的距離，則該數據對象仍在原來簇中。因此，不需要計算到剩余聚類中心的距離，節省了計算到剩余聚類中心距離的時間。本文將該文獻中提到的改進算法的思想引入到最小方差優化初始聚類中心K-means算法中，在避免選擇初始質心隨機選取的同時縮短聚類時間。

2.1 幾個相關的基本概念

定義1：樣本之間的歐氏距離：

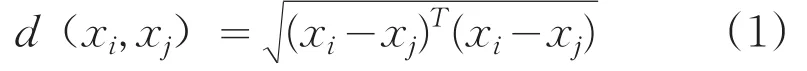
定義2：樣本xi到所有樣本距離的均值：

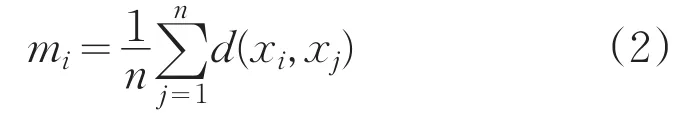
定義3：樣本xi的方差：

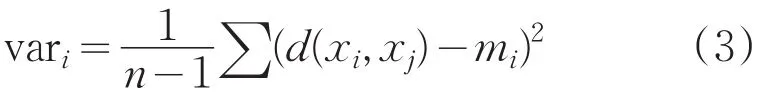
定義4：所有數據樣本的平均距離：

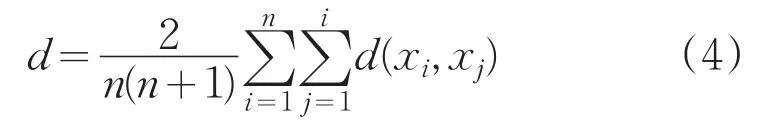
定義5：聚類準則函數：

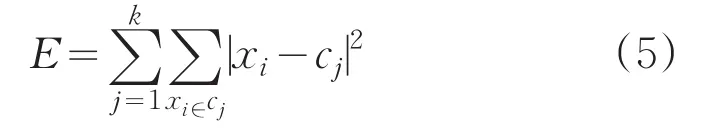
2.2 算法執行過程

改進算法的執行過程描述如下：

（1）選擇初始聚類中心

1）根據定義1計算數據對象間距離；

2）根據1）中計算出來的數據對象間距離以及定義4計算平均距離d；

3）計算每個樣本方差并選取方差最小的那個樣本作為第一個聚類中心；

4）把與已有聚類中心距離大于平均距離d的樣本方差置空，在剩余樣本方差中選取最小的那個樣本作為下一個聚類中心；重復該步，得到k個聚類中心，執行（2）；

（2）執行改進后的K-means算法：

1）計算每個數據樣本到各個初始聚類中心的距離，按最近離原則將其分到各個簇，存儲每個數據對象的類標簽和對象到最近中心點的距離到cluster［］和dis［］中；

讓cluster［i］=j，j為對象i最近的簇標簽；

讓dis［i］=d（xi，cj），d（xi，cj）為到最近中心點的距離；

2）按照平均法計算各簇的質心，得到新的簇中心；

3）計算準則函數E；

（3）重復以下過程

1）計算每個數據對象到新聚類中心的距離d；

a）如果 d ＜=dis［i］，則第 i個數據對象仍近似的在原來的簇中，將該數據對象分給原來的簇。

b）否則，計算數據點到所有中心的距離d(xi,ck)，分配數據到最近的簇中心；讓

cluster［i］=k ，dis［i］=d(xi,ck)；

2）更新簇中心

3）計算準則函數E，判斷E是否收斂，若收斂，則算法結束，輸出最終聚類結果。

由前面對最小方差優化初始聚類中心K-means算法的復雜度分析可知，選取初始質心的復雜度為O（n2），在進行數據分配時，首先將N個數據對象分到k個簇，計算量為O（nk），在后面的迭代計算過程中，一些數據對象仍近似的保留在原來的簇中，而一些數據對象將分配到其它的簇中。如果數據點仍近似的留在原來的簇中，時間復雜度為O（1），否則，為O（k）。隨著算法的不斷收斂，每個簇中移動的數據點的數量也在不斷減少，如果有一半的數據移動，此時的時間復雜度為O（nk/2），因此在進行數據分配時的總的時間復雜度為O（nk t2），其中t2為迭代次數，因此本文算法總的時間復雜度為O（n2）。

3 實驗測試及結果分析

本文在UCI數據庫中取5個不同的數據集進行測試，給出了數據集描述表以及各個算法的時間復雜度對比表，并對本文算法中的優化方法進行描述。各個算法在數據集運行30次得出實驗結果，在聚類準則函數E上對傳統K-均值，快速全局K均值、最小方差K均值算法，以及本文改進算法進行實驗結果的比較；在運行時間上本文算法首先與前兩種方法進行比較；由于本文算法與最小方差K均值選取初始質心的計算方法相同，則選取初始質心的時間上也相同，算法的提速主要是在后續聚類，因此，對兩種算法運行時間的比較分兩方面：選取初始質心時間T1與數據聚類時間T2，主要是對數據聚類時間進行比較。給出算法本身的迭代次數t，然后對各個算法的時間復雜度進行了對比分析。數據集描述如表1所示，時間復雜度對比如表2所示，實驗結果的比較分別如表3、表4、表5所示。

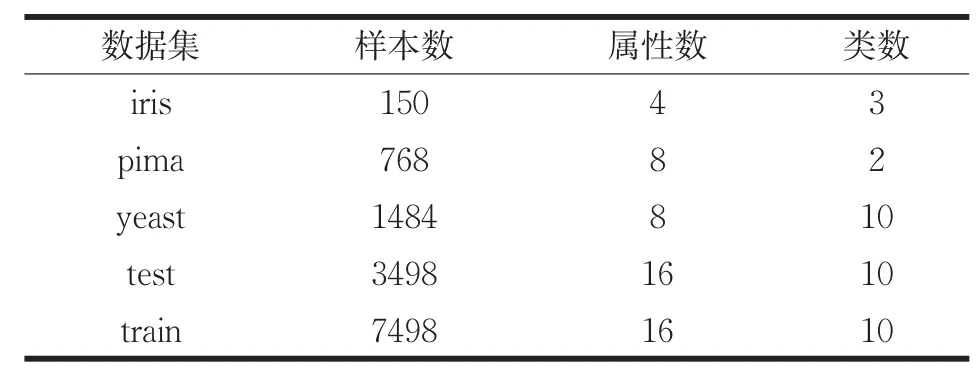
表1 數據集描述表

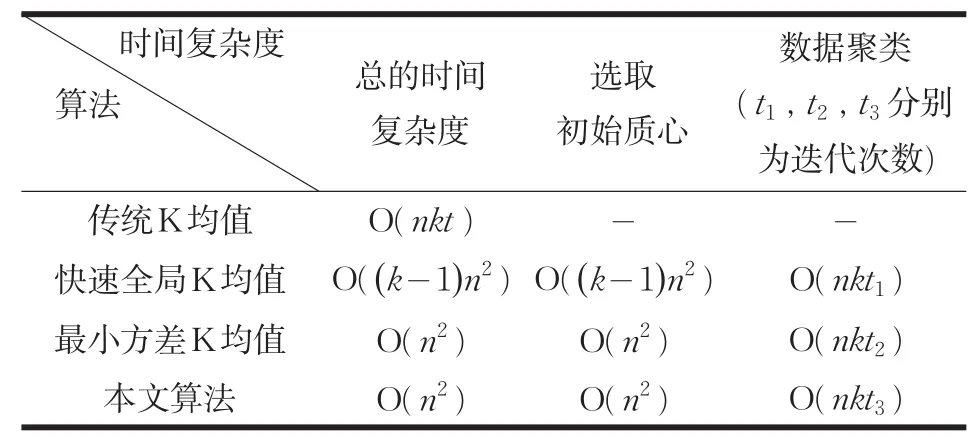
表2 時間復雜度對比

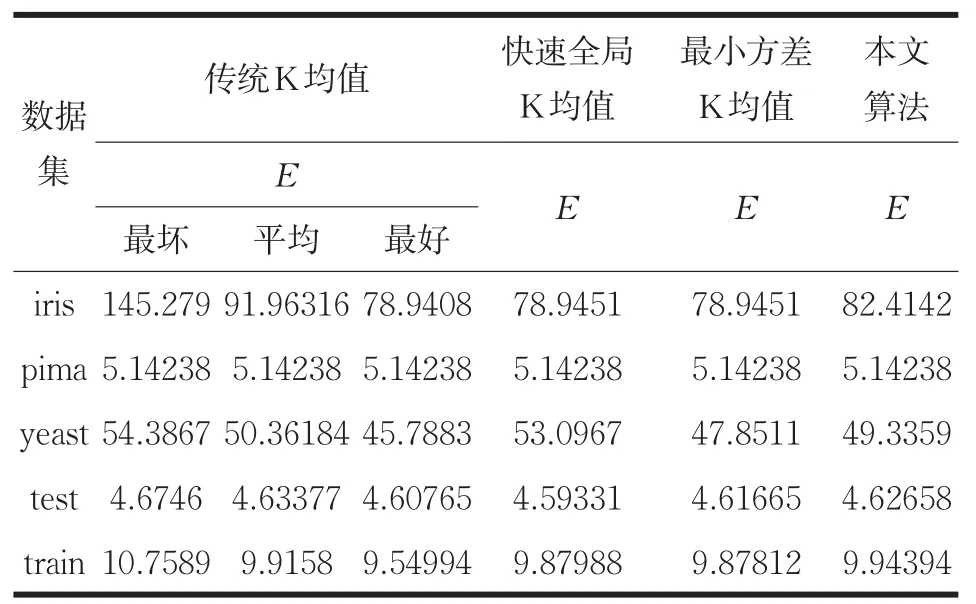
表3 各算法準則函數E上的比較

由表3可知，在pima數據集上，本文算法與最小方差優化初始聚類中心的K-means算法以及快速全局K-means算法保持了聚類結果的一致性。在yeast數據集上，本文算法聚類誤差平方和略高于改進前算法，但優于快速全局K-means算法。在其它數據集上與最小方差優化初始聚類中心的K-means算法相比E雖然有所增大，但都接近于傳統K-means算法最好或平均聚類誤差平方和。由以上分析可知，本文算法基本上沒有影響聚類結果，證明了改進后算法的有效性。

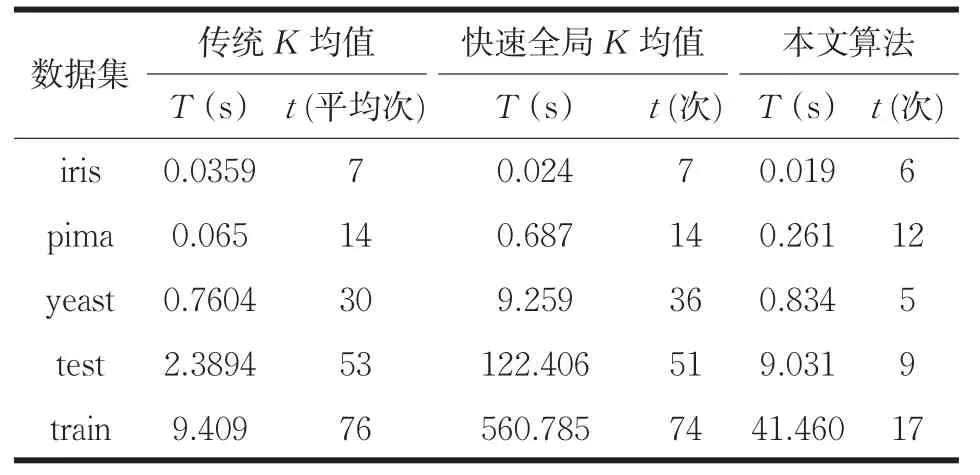
表4 各算法運行時間T上的比較

根據表2和表4的對比，可知本文算法與快速全局K均值的時間復雜度大于傳統K均值，本文算法的時間復雜度小于快速全局K均值。由于通過計算的方法選取初始聚類中心相對于隨機選取初始質心會消耗一部分運行時間，并且隨著數據量的增大，選取初始質心的時間消耗增長，因此就表3中的所有數據集而言，快速全局K均值，以及本文算法不如K-means算法運行時間效率高，但本文算法的運行時間效率高于快速全局K均值。

由表2知本文算法選取初始質心的時間復雜度小于快速全局K均值選取初始質心的時間復雜度。在進行數據分配聚類時，本文算法的優化方法是通過存儲每個數據對象的類標簽以及與所屬類中心的距離，在下一次迭代中，計算數據點與所屬類中更新后的聚類中心的距離，若小于與原來聚類中心的距離，則近似的將該數據對象分給原來的簇，減少到其余k-1個中心距離的計算。隨著迭代的進行，所需移動的數據點的個數在不斷減少，在數據聚類時，需要與所有聚類中心計算距離的計算量減少，并且由于每個簇中數據點的變化減小，使得簇達到穩定所需的迭代次數也相對減少，縮短了算法收斂所需要的時間。

如表4所示，由于iris與pima兩個數據集的數據量與簇的數目較少，算法的迭代次數變化不大，在其余三個數據集上，算法收斂的迭代次數都有明顯的減少。迭代次數的減少以及本文算法選取初始質心與數據聚類所需的計算量小，使得算法的整體運算效率要明顯高于快速全局K均值。

由于本文算法與最小方差k均值選取初始聚類中心的計算方法相同，選取初始質心時間T1相同，算法的提速主要是在后續聚類，因此本文算法主要在數據聚類時間T2上進行比較。根據上面對本文算法進行數據聚類時優化方法的描述可知，本文算法在已選出初始聚類中心的情況下，對數據點進行分配歸類時，減少了數據點與聚類中心計算距離的計算量以及算法收斂所需的迭代次數，縮短了數據聚類所需的聚類時間。由表5可以看出，隨著數據集的增大，聚簇數目的增多，算法收斂所需的迭代次數明顯減少，本文算法相對于最小方差K均值的運算效率也有明顯的提高，在iris與pima數據集上，進行數據聚類時的運算速度提高了40%～50%，在剩余的三個數據集上，進行數據分配歸類時，進行數據聚類時的運算速度提高了70%～90%，可見，改進后的算法明顯縮短了數據分配歸類所需的聚類時間，證明了改進后算法在時間性能上的高效性。

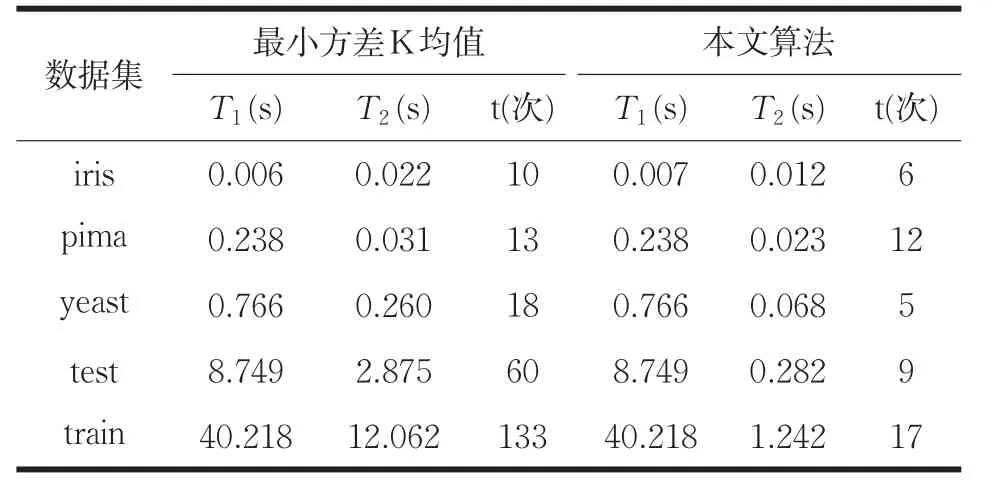
表5 本文算法與最小方差K均值的運行時間比較

綜上所述，快速全局K均值，最小方差K均值以及本文算法的時間復雜度大于傳統K均值的時間復雜度，但這三種方法都是通過計算來獲得穩定的初始質心，由表3可知，這三種算法的聚類結果相對于傳統K均值算法的聚類結果，更具有穩定性和準確性。由表2、表4可知，本文算法的時間復雜度優于快速全局K均值，算法的整體運行效率明顯高于快算全局K均值。本文算法與最小方差K均值相比，由于兩種算法選取初始聚類中心的計算方法相同，選取初始質心的時間相同，主要是對后續的數據聚類進行優化提速，由上面的分析可知，本文算法相對于最小方差K均值算法，減少了后續聚類的計算量以及算法收斂所需的迭代次數（如表5所示），證明了本文算法在時間性能上的高效性。

4 總結

本文通過將一個簡單有效的數據聚類方法引入到最小誤差優化初始聚類中心的K-means算法中，在避免隨機選取初始聚中心導致聚類結果不穩定的基礎上，減少了計算量，提高算法的執行效率，并在UCI數據集進行了實驗驗證，實驗結果證明了改進算法在聚類結果上的有效性以及在聚類時間上的高效性。

［1］Han Jiawei，Kamber M.Data mining：concepts and techniques［M］.Beijing：China Machine Press，2011.

［2］Shunye W.An improved k-means clustering algorithm based on dissimilarity［C］//Mechatronic Sciences，Electric Engineering and Computer（MEC），Proceedings 2013 International Conference on IEEE，2013：2629-2633.

［3］Xu J，Xu B，Zhang W.Stable initialization scheme for k-means clustering［J］.Wuhan University Journal of Natural Sciences，2009，14（1）：24-28.

［4］Redmond S J，Heneghan C.A method forinitializing the K-means clustering algorithm using kd-trees［J］.Pattern Recognition letters，2007，28（8）：965-973.

［5］謝娟英，王艷娥.最小方差優化初始聚類中心的K-means算法［J］.計算機工程，2014，40（8）：205-211.

［6］Likas A，Vlassis M，Verbeek J.The global K-means clustering algorithm［J］.Pattern Recognition，2003，36（2）：451-461.

［7］Na S，Xumin L，Yong G.Research on k-means clustering algorithm：An improved k-means clustering algorithm［C］//Intelligent Information Technology and Security Informatics（IITSI），2010 Third International Symposium on IEEE，2010：63-67.