基于波形結構特征和支持向量機的水面目標識別

孟慶昕 楊士莪 于盛齊

1 引言

通常情況下，艦船輻射噪聲主要由機械噪聲和螺旋槳噪聲組成。哪一種作為決定因素取決于目標船的工況。不同類別的目標從動力系統到機械結構，再到工作狀態都存在顯著區別。同一類的目標輻射信號總是表現一定程度的相似性，而不同類別目標信號則表現差異性，這為識別不同類別的水聲信號奠定了基礎[1]。借鑒語音聲學的研究成果，音色可作為區分不同目標的依據。由于時域波形結構特征隱含了音色信息[2]，所以可用來區分不同類別的水面目標信號。

近年來，機器學習算法是數據分析領域的一個研究熱點，而支持向量機（SVM）效果頗豐。文獻[3]應用 SVM 對稀疏表示的水聲目標特征集進行識別，大幅度提高目標識別速度；文獻[4]將水平集獲取的特征矢量輸入SVM識別圖像聲吶信號；文獻[5]提出一種基于核層面信息融合的雷達輻射源個體識別框架；文獻[6]建立多維分形和 SVM 的模型，提高了智能地雷對地面裝甲目標的識別準確率。在生物醫學工程領域，SVM用于肢體肌電信號的特征提取與分類[7]。構建SVM分類器，參數優化選取是關鍵。常用參數尋優算法包括：網格搜索法，遺傳算法（Genetic Algorithm, GA）[8]，以及粒子群算法（Particle Swarm Optimization, PSO）[9,10]等。網格搜索法原理簡單，通過遍歷網格搜索全局最優解，但可操作性差。GA和PSO算法不必遍歷搜索參數，即可獲得全局最優解，但容易陷入局部最優解，因此需要在常規的方法基礎上加以改進。

2 原理和方法

2.1 波形結構

波形結構特征提取應用了搜尋極值、過零點以及統計分布等方法，極大地壓縮了數據，反映了模式的本質特征。

波形結構主要包含4個方面特征：過零點波長，峰峰幅度，過零點波長差分以及波列面積。統計樣本序列的過零點波長數，用 S （ αi） 表示過零點波長為αi的個數。則過零點波長為αi的概率分布函數為

H = m ax（Ak）代表樣本序列的最大峰峰幅度。所有的峰峰幅度值被H歸一化，并在取值范圍內的20個均分區間統計分布。用 βi（i = 1 ,2,… ,2 0） 表示任意區間， S （ βi）代表落在區間 βi的峰峰幅度值的個數，則峰峰幅度的概率分布函數為

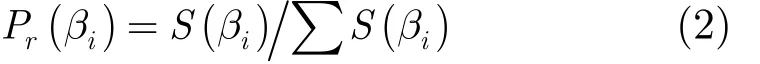
θi表示任意相鄰兩個波長差，S （ θi）計算過零點波長點差為θi的數目，則過零點波長差的概率分布函數為

波列面積是由水平軸和時域波形圍成的圖形面積，可以用一系列長方形來近似表示。設波列面積的最大值為 S =max （ Rk），將歸一化之后的波列面積區間均分為20等份，ξi（i= 1,2,… ,20）表示任意區間。設落在ξi區間的波列面積數目為S（ ξi），則波列面積的概率分布函數為

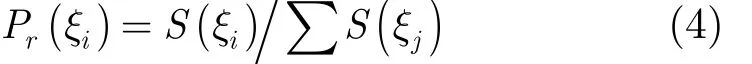
根據以上時域波形結構的4種統計特性，構建一個9維的波形特征矢量，包含如下:

（1）平均過零點波長的概率密度；

（2）過零點波長分布概率最大值；

（3）過零點波長分布概率最大值對應的波長值；

（4）過零點波長差分分布概率最大值對應的差分值；

（5）歸一化波列面積為0到p1的概率和；

（6）峰峰幅度概率值在 0到 q1的所有值的概率和；

（7）峰峰幅度概率值在 q1到 q2的所有值的概率和；

（8）峰峰幅度概率值在 q2到 q3的所有值的概率和；

（9）歸一化峰峰幅度值在 0 到 p1范圍內的所有值的概率和。

其中 0＜p1＜1, 0＜q1＜q2＜q3＜1。

過零點波長分布反映信號的頻率高低，峰峰幅度分布反映信號幅度的起伏程度，過零點波長差的分布反映信號的頻率變化快慢，波列面積分布綜合反映信號頻率和幅度起伏信息。音色是聲信號時頻變化的綜合體現。波形結構特征描述了隱含的音色信息，符合人耳感知的聽覺特征。

2.2 支持向量機

支持向量機（SVM）是參數識別和分類領域一種很有效的研究方法。其基本觀點為將信號從樣本空間轉化到特征空間，確定優化超平面（邊界）函數，使得兩類目標信號之間距離最大化[11]。如圖1所示，分類間隔是超平面到兩類目標數據最近點的距離，該點即支持向量的距離[12]。也就是說，SVM分類器的目標是在高維特征空間獲得最優分離超平面[13]。

SVM 分類器的核函數有很多種，包括線性函數，多項式核函數，sigmoid 核函數以及徑向基函數（RBF）等。本文設置的核函數為 RBF 核函數（K（ x, y）=e-γx-y2, γ ＞0）。RBF核將樣本信號以非線性方式轉換到高維特征空間。經證實，RBF核函數和其他的線性核函數表現出類似的性能，同時RBF核的參數較多項式核函數更少，從而降低了模型的復雜度。

2.3 交叉驗證法

SVM 模型的泛化能力通常用經典的交叉驗證法評價。k折交叉驗證法的原理是將數據分成k個子集。每次用其中的一個子集作為測試集，而其他k- 1個子集作為訓練集。先用訓練集中的數據訓練分類器模型，再用得到的 SVM 分類器對測試集的數據進行測試。每個數據點都會出現在測試集1次，出現在訓練集k -1次。隨著k的增加，結果估計的均方值會隨之減小。將k次交叉驗證的預測準確率平均值作為衡量模型推廣能力的標準。交叉驗證法避免了過學習和欠學習的問題。

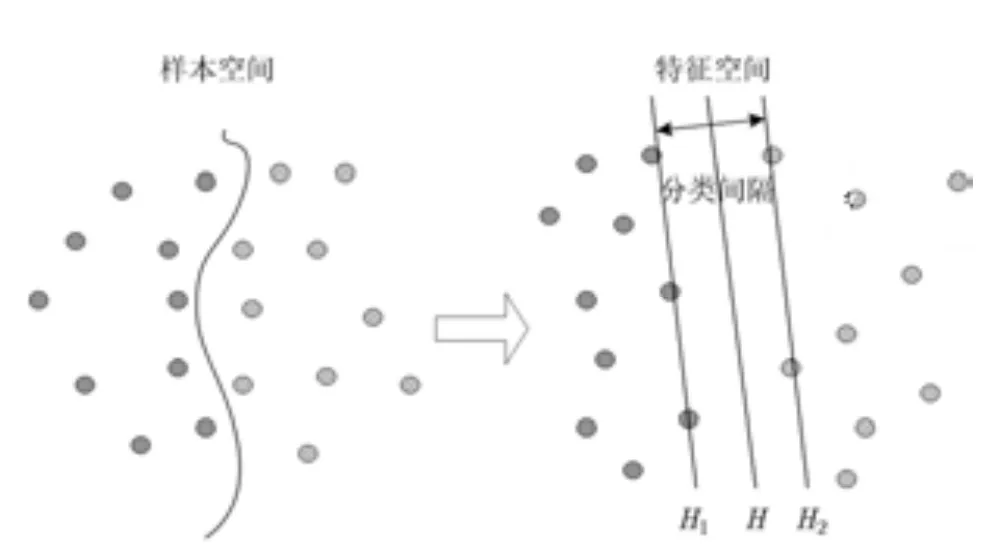
圖1 SVM的基本原理圖

2.4 參數選取方法

2.4.1 網格搜索法 基于RBF核的SVM的性能主要受懲罰因子C和核參數γ的影響。核函數主要反映樣本數據在高維空間的復雜程度，即維數[13]。而懲罰因子通過調節特征空間中置信范圍和經驗風險的比例，使SVM的泛化能力達到最好。SVM的性能優化轉化為參數對（C , γ ）的優化選擇問題。

對于參數搜索，目前尚未有公認的最有效方法。網格搜索法由于原理簡單，是搜索 SVM 一種常用方法。該方法的過程如下：首先，根據經驗，確定參數γ和C的搜索范圍；其次，恰當選取搜索步長，得到一系列的參數對（C , γ ）；然后，每一組參數對被用來訓練 SVM 模型；最后，挑選使訓練序列的預測精度達到最大的SVM參數對（C, γ），即得到泛化能力強的 SVM 分類器。換言之，網格搜索方法是應用海量搜索獲得最優解的。比如，若γ和C參數的候選值分別為m和n，則對（C , γ ）的2維參數空間被劃分為m×n個網格。該種方法理論上，在參數搜索范圍足夠大、搜索步長足夠小的情況下是可以得到全局最優解的。但是搜索時間較長，且由于采取逐步逼近的方法，花費在非最優解區域的時間過長，是不可忽視的。

2.4.2 優化算法 在對參數對（C, γ）進行選擇時，優化算法是必不可少的。常用的優化算法包括遺傳算法、差分進化算法（Differential Evolution, DE）以及粒子群優化（PSO）算法等。DE算法具有較強的全局收斂能力和魯棒性，可以避免遺傳算法的早熟缺點。然而，DE算法隨著迭代次數的增加，優化效率逐漸降低，迭代后的個體收斂程度差，可能出現發散的結果[14]。粒子群算法具有收斂速度快的特點，迭代后群體中的粒子收斂（或集中）程度非常高，每個粒子搜索到的最優位置在計算和顯示精度內基本上處于同一點，粒子會很快地失去種群多樣性，容易陷入局部最優[15]。

本文采用一種基于DE算法和PSO算法的混合優化算法 DEPSO。該算法使群體能夠保持一定的多樣性，既不像PSO算法那樣所有粒子很快收斂于同一位置，也不像DE算法那么發散，而是所有個體逐漸趨向于同一點，并保有多樣性的潛能。同時還可以進一步根據收斂程度對最終的最優解進行取舍，即將迭代后收斂程度相對不高情況下的最優解舍棄。

在對群體進行初始化時，每個個體根據搜索范圍隨機產生：

DEPSO算法首先按照DE算法進行搜索，然后將DE算法得到的最后一代群體作為PSO算法粒子的初始位置和每個粒子搜索到的局部最優位置的初始值，迭代后所有代中的最優個體作為PSO算法所有粒子迄今為止搜索到的全局最優位置的初始值。其中，DE算法中所有代的最優個體的獲取方法如同PSO算法對全局最優位置的更新方式一樣，每迭代一次后都通過目標函數值的比較進行保留或更新。PSO算法中粒子的初始速度同樣根據搜索范圍隨機產生，根據Clerc的速度更新公式[16]，可表示為

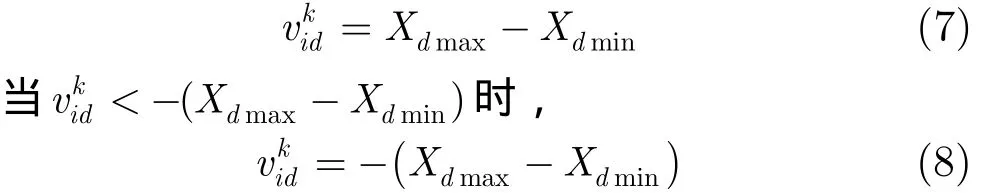
并且，在搜索過程中對于移動到搜索空間外的個體，對其位置進行隨機分配，當＞X時，d dmax

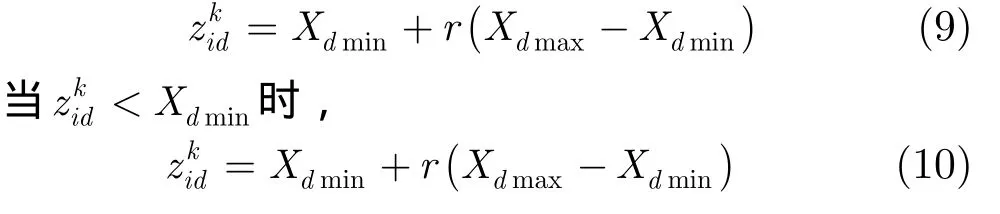
這樣整個DEPSO算法實際上是在DE算法搜索到的全局最優附近，采用PSO算法進行局部的精確搜索，并進一步提高群體的收斂程度。

3 實驗與分析

3.1 波形結構

對比分析兩類水面目標信號結構特征參數。分別提取兩類目標信號的過零點波長、峰峰幅度、過零點波長差分以及波列面積，統計其結果，繪制概率密度函數曲線。目標輻射噪聲的數據十分寶貴，尤其是水下目標信號。但由于條件所限，目前尚缺少多目標，不同工況下的目標輻射噪聲數據。

如圖2至圖5所示，兩類目標信號從過零點波長特征、歸一化的峰峰幅度特征、過零點波長差分以及歸一化的波列面積等特征進行對比，發現針對同一特征兩類目標信號特征值的取值范圍和極值大小均存在明顯差異。根據圖2至圖5的4個特征，提取9維特征值，構成特征矢量，輸入到SVM分類器。為了簡便，以下分別以目標1和目標2代指商船和水面運輸機。

3.2 支持向量機

對目標信號截取的每一時域波形提取9維波形結構特征。則輸入SVM分類器的樣本共有240組，其中120組來自目標1，其它的120組來自目標2。輸入的240組樣本被分割為兩部分，其中一部分作為訓練樣本，訓練分類器獲得最優 SVM 參數，另一部分作為測試樣本，作為估算分類精度的依據。測試樣本和訓練樣本各自所占的比例影響了分類精度，在下一節作詳細的討論。

3.3 分類結果

應用SVM分類器對目標1和目標2進行分類實驗，核函數為 RBF。核寬度參數γ和懲罰因子C需適當選取，才能獲得最佳的分類性能。本文分別應用常用的網格搜索方法和DEPSO法搜索參數對（C,γ）。 調用MATLAB 工具箱LIBSVM驗證了最優參數下的SVM分類器的性能。

從4個方面提取數據的時域波形結構特征，構建9維特征矢量，240組特征矢量作為SVM分類器的輸入量。每一組時域波形的長度為0.5 s，采樣頻率為10 kHz。懲罰因子C 的搜索范圍為 [2-5210]，核寬度參數 g 的搜索范圍為 [2-1026]。C 和γ的搜索步長均為0.5。應用5-折交叉驗證法驗證SVM分類器的性能，則分類結果如圖6所示。

圖2 歸一化的過零點波長分布曲線

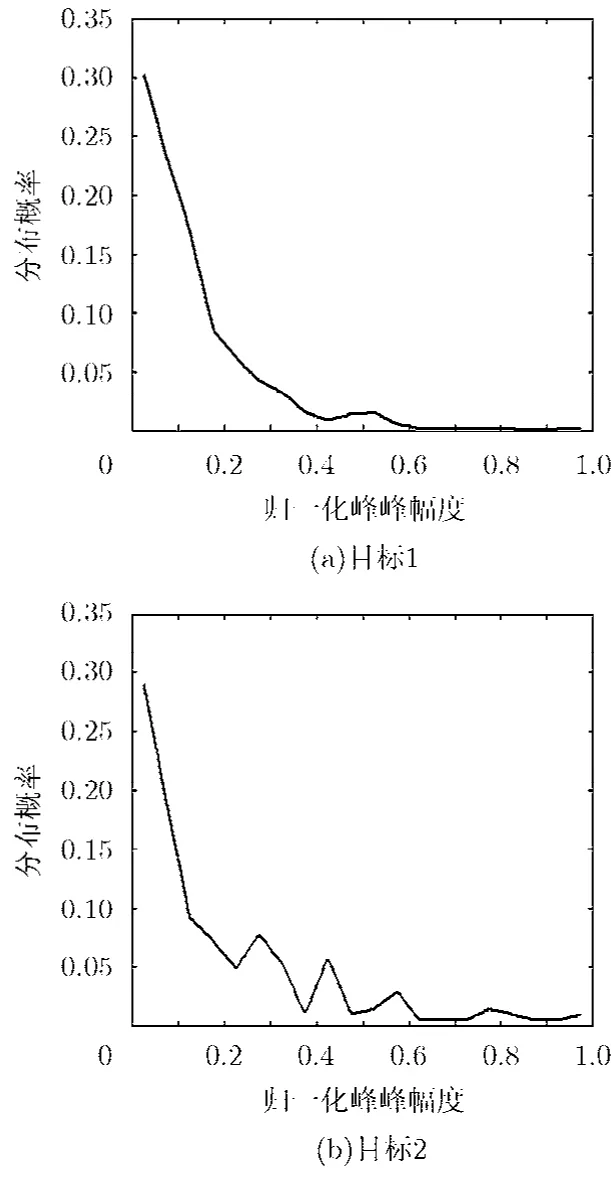
圖3 歸一化的峰峰幅度分布曲線

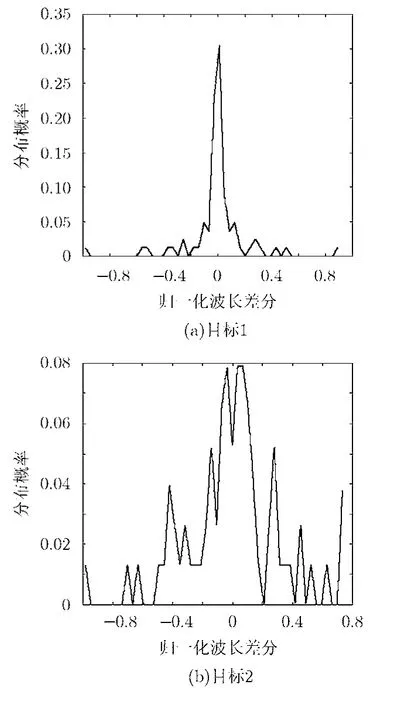
圖4 歸一化的過零點波長差分分布曲線

圖5 歸一化波列面積分布曲線

圖6 網格法搜索最優參數

網格搜索最優參數結果如圖6所示。橫軸代表懲罰因子，縱軸代表核函數寬度，均以對數坐標表示。圖中所給出的是平均識別準確率的等高線圖。如圖6所示，參數C和參數 γ只覆蓋了圖中網格的部分區域，這說明參數只在特定區域取值。同時，最優參數對不能直接從圖上選取最大識別率對應點讀出，因為過大的懲罰因子可能會造成訓練樣本的過學習現象。也就是說，在分類準確率同為最高的條件下，懲罰因子C 更小的參數對是優化解。

DEPSO法搜索最優參數的結果如圖7所示。x軸代表懲罰因子，y軸代表核函數寬度，均以對數坐標表示。z軸代表目標函數，即測試數據的分類識別精度。根據優化算法DEPSO的特點，由收斂程度對最終的最優解進行取舍，即將迭代后收斂程度相對不高情況下的最優解舍棄，此時最優解的精度往往較低。反復進行50次參數搜索實驗，選取其中散點個數較少、一致收斂的結果作為全局最優解。由圖6和圖7的對比可知，由于優化算法實際是在全局最優解附近搜索，故目標函數值（除極少的散點）都維持在較高的取值，避免了網格搜索法在不關心區域的盲目搜索問題。

根據表1中的分類結果，SVM分類器的性能受測試數據比例的影響。當訓練序列數目較小時 （占輸入數據的50.0%, 第3行），兩類目標的分類平均準確率（測試數據）為67.5%。當訓練序列數目增加到輸入數據的75.0%時，平均識別精度增加到 88.3%。當訓練序列數目增加到87.5%時，平均識別精度僅增加到90%。結果表明提高訓練樣本數目可以幫助得到更高的分類精度，這從統計意義上很好理解。但是過大的訓練樣本數卻是不符合實際情況的。

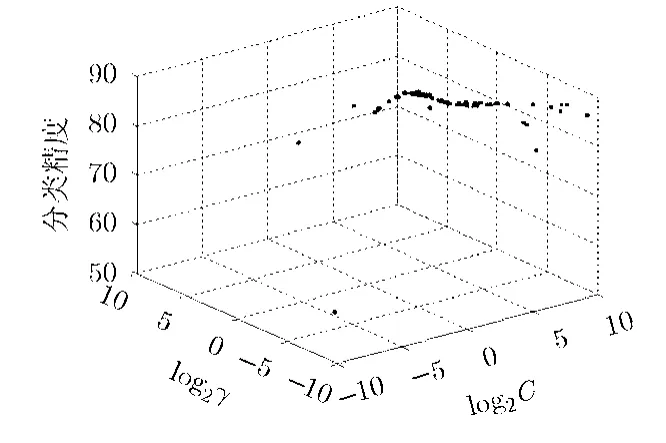
圖7 DEPSO法搜索最優參數

在某些情況下，需要兩次搜索獲得最優參數對。由于缺少先驗知識，首先在較大的區間范圍，以較大的步長，獲得一個全局最優參數。然后在獲得的最優參數對附近，以更小的步長，第2次搜索最優參數對。表2和表3是一個二次搜索獲取二分類實驗最優參數對的算例。訓練樣本占實驗數據總數75%。第1次搜索，搜索步長為0.5 ，得到一組全局最優參數對（C1,1γ）。第2次搜索，僅在區間[C1/4,4 C1]和[1γ/4,41γ]組成的網格搜索最優參數，搜索步長為0.1。結果表明，第1次搜索的初始區間對最終的分類結果有很大的影響，這帶有一定的經驗成分。第2次搜索在第1次尋得的最優參數附近，減小了搜索步長，獲得了更精細的結果。理論上，搜索范圍足夠大、搜索步長足夠小的情況下，該方法可以獲得全局最優參數，但可操作性差。

表 1 網格搜索法分類結果

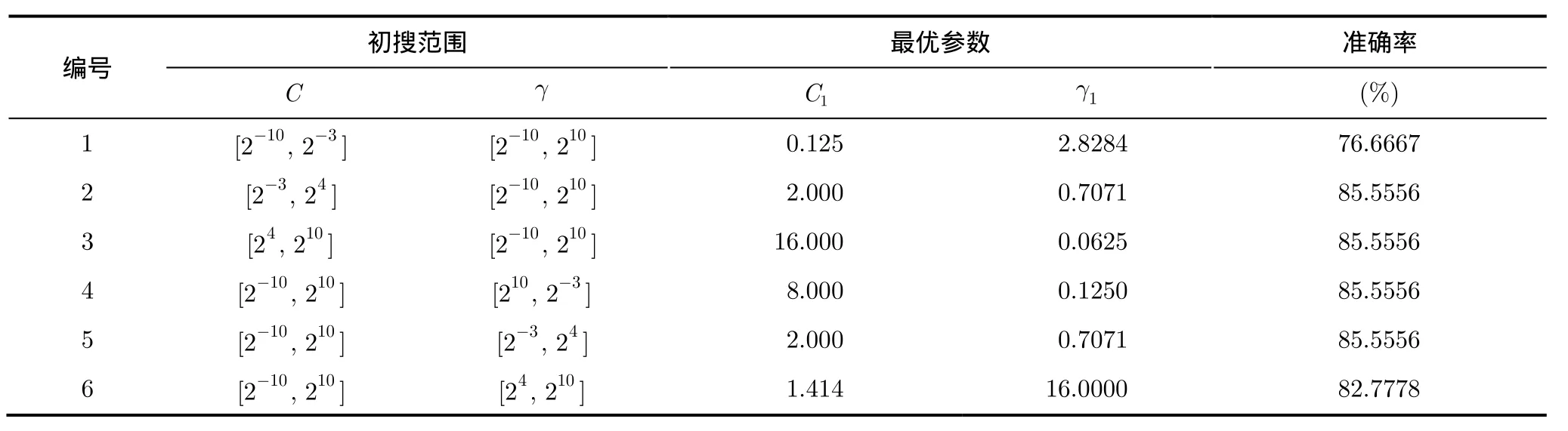
表2 第1次搜索結果

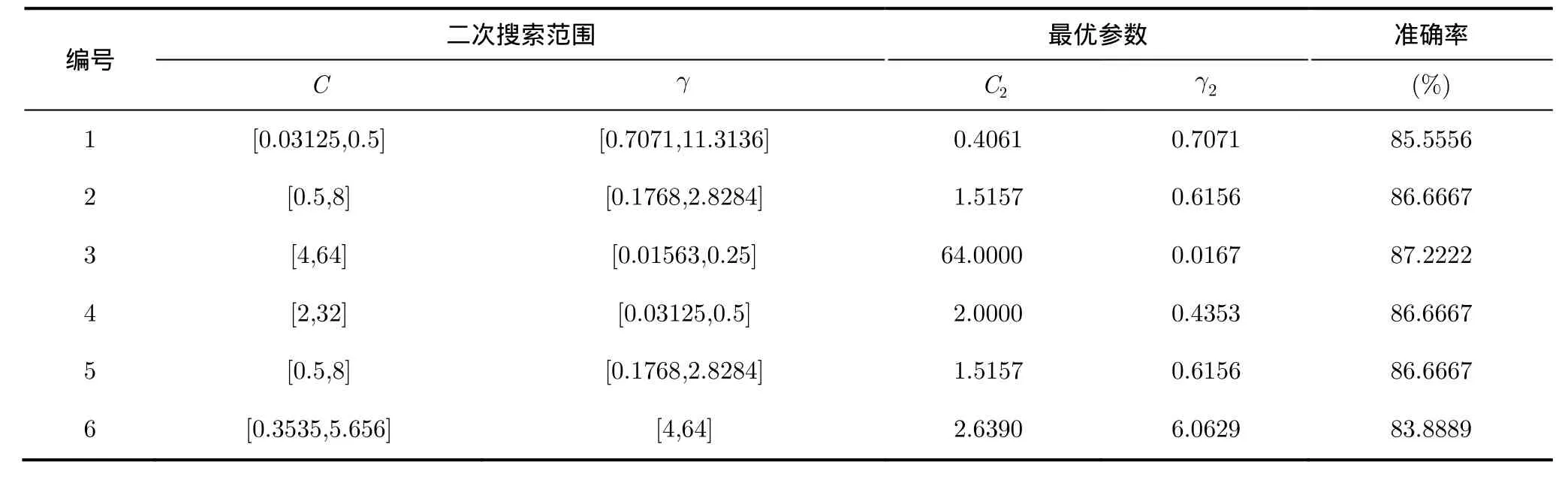
表3 第2次搜索結果

如表4所示，應用優化算法DEPSO尋得最優參數對（C,γ）構建SVM分類器，對測試數據進行分類識別實驗。與表1中實驗相同的輸入數據，在訓練樣本占實驗數據總數分別為87.5%, 75.0%, 66.7%和 50.0%的情況下，應用優化算法后得到的分類精度依次為100%, 88.33%, 86.25%和72.5%，比網格搜索方法整體有了較顯著的提高。同時，由于DEPSO避免了遍歷搜索，搜索范圍的設置對結果的影響大大降低。DEPSO方法更加切實有效，其優勢是十分明顯的。值得一提的是，兩次搜索法涵蓋了 [2-10210]和 [2-10210]組成的網格。由于在 C＜2-6, γ＞27的情況下無法尋得有效結果，在本部分討論中將該部分網格舍棄。故表2、表3和表4的結果具有可比性。

4 結束語

本文對水面目標時域波形結構特征提取方法進行了研究。在4種信號統計特性（過零點波長特征，峰峰幅度特征，過零點波長差分以及波列面積特征）的基礎上，構建了9維的特征矢量。將特征矢量輸入 SVM 分類器對水面目標信號進行分類識別。該特征提取方法符合人的主觀感受，具有實際意義。提出了差分進化粒子群混合算法（DEPSO），通過對懲罰因子和核函數寬度參數的優化選取，達到了優化系統 SVM 模型的目的，并將結果與網格搜索法進行比較。改進優化方法 DEPSO 搜索參數融合DE算法和PSO算法的優點，避免了網格搜索法的盲目搜索，更切實有效，具有尋優速度快、精度高、收斂效果好等特點。在缺少先驗知識的情況下，獲得了更高的識別率。

海試數據驗證了以上分類識別方法的有效性。值得一提的是，表中所列的結果是兩個目標多組信號的統計平均結果，具有典型意義。目標輻射噪聲的數據十分寶貴，尤其是水下目標信號。但由于條件所限，目前尚缺少多目標、不同工況下的目標輻射噪聲數據。故僅在此作為一種可試行的水面和水下目標識別方法探究，擬于今后進一步豐富實驗檢驗。

表 4 DEPSO法分類結果

[1] 王志偉. 水下目標被動識別技術方法研究[D]. [碩士論文],哈爾濱工程大學, 2002.Wang Zhi-wei. The recognition study of passivity target[D].[Master dissertation], Harbin Engineering University, 2002.

[2] 蔡悅斌, 張明之, 史習智, 等. 艦船噪聲波形結構特征提取及分類研究[J]. 電子學報, 1999, 27（6）: 129-130.Cai Yue-bin, Zhang Ming-zhi, Shi Xi-zhi, et al.. The feature extraction and classification of ocean acoustic signals based on wave structure[J]. Acta Electronica Sinica, 1999, 27（6）:129-130.

[3] 廖明熙, 張小薊, 張歆. 基于稀疏表示的水聲信號分類識別[J]. 探測與控制學報, 2014, 36（4）: 67-70.Liao Ming-xi, Zhang Xiao-ji, and Zhang Xin. Classification and recognition of underwater acoustic signal based on sparse representation[J].Journal of Detection & Control, 2014, 36（4）:67-70.

[4] 許文海, 續元君, 董麗麗, 等. 基于水平集和支持向量機的圖像聲吶目標識別[J]. 儀器儀表學報, 2012, 33（1）: 49-55.Xu Wen-hai, Xu Yuan-jun, Dong Li-li, et al.. Level-set and SVM based target recognition of image sonar[J].Chinese Journal of Scientific Instrument, 2012, 33（1）: 49-55.

[5] 史亞, 姬紅兵, 朱明哲, 等. 多核融合框架下的雷達輻射源個體識別[J]. 電子與信息學報, 2014, 36（10）: 2484-2490.Shi Ya, Ji Hong-bing, Zhu Ming-zhe, et al.. Specific radar emitter identification in multiple kernel fusion framework[J].Journal of Electronics & Information Technology, 2014,36（10）: 2484-2490.

[6] 丁凱, 方向, 張衛平, 等. 基于聲信號多重分形和支持向量機的目標識別研究[J]. 兵工學報, 2012, 33（12）: 1521-1526.Ding Kai, Fang Xiang, Zhang Wei-ping, et al.. Target identification of acoustic signals based on multi-fractal analysis and support vector machine[J]. Acta Armamentarii,2012, 33（12）: 1521-1526.

[7] 張啟忠, 席旭剛, 羅志增. 基于非線性特征的表面肌電信號模式識別方法[J]. 電子與信息學報, 2013, 35（9）: 2054-2058.Zhang Qi-zhong, Xi Xu-gang, and Luo Zhi-zeng. A pattern recognition method for surface electromyography based on nonlinear features[J]. Journal of Electronics & Information Technology, 2013, 35（9）: 2054-2058.

[8] Chen Ping-wei, Wang Yung-ying, and Lee Ming-hahn. Model selection of SVMs using GA approach[C]. Proceedings of 2004 IEEE International Joint Conference on Neural Networks,Pscataway, NJ, 2004: 2035-2040.

[9] 周紹磊, 廖劍, 史賢俊. RBF-SVM 的核參數選擇方法及其在故障診斷中的應用[J]. 電子測量與儀器學報, 2014, 28（3）:240-246.Zhou Shao-lei, Liao Jian, and Shi Xian-jun. Kernel parameter selection of RBM-SVM and its application in fault diagnosis[J]. Journal of Electronic Measurement and Instrumentation,2014, 28（3）: 240-246.

[10] 鄭適, 張安學, 岳思橙, 等. 基于改進粒子群優化的探地雷達波形反演算法[J]. 電子與信息學報, 2014, 36（11）: 2717-2722.Zheng Shi, Zhang An-xue, Yue Si-cheng, et al.. Ground penetrating radar inversion algorithm based on improved particle swarm optimization[J]. Journal of Electronics &Information Technology, 2014, 36（11）: 2717-2722.

[11] Fernandez P J A, Baeten V, Renier A M, et al.. Combination of support vector machines （SVM） and near-infrared （NIR）imaging spectroscopy for the detection of meat and bone meal（MBM） in compound feeds[J]. Journal of Chemometrics,2004（18）: 341-349.

[12] Cristianini N and Taylor J S. An Introduction to Support Vector Machines and Other Kernel-based Learning Methods[M]. Cambridge: The Press Syndicate of the University of Cambridge, 2001: 93-94.

[13] 廖曉晰. 動力系統的穩定性理論和應用[M]. 北京：國防工業出版社, 2000: 169-199.Liao Xiao-xi. Stability Theory and Application of Power System[M]. Beijing: National Defence Industry Press, 2000:169-199.

[14] 楊坤德. 水聲陣列信號的匹配場處理[M]. 西安: 西北工業大學出版社, 2008: 32-39.Yang Kun-de. Matched Field Processing of Underwater Acoustic Array Signals[M]. Xi’an: Press of Northwestern Polytechnical University, 2008: 32-39.

[15] 紀震，廖惠連，吳青華. 粒子群算法及應用[M]. 北京: 科學出版社，2009: 169-199.Ji Zhen, Liao Hui-lian, and Wu Qing-hua. Application of Particle Swarm Algorithm[M]. Beijing: Science Press, 2009:169-199.

[16] Clerc M. The swarm and the queen: towards a deterministic and adaptive particle swarm optimization[C]. Proceedings of the Congress of Evolutionary Computation. Washington,USA, 1999: 1951-1957.