一種主用戶隨機(jī)到達(dá)情況下改進(jìn)的循環(huán)平穩(wěn)特征檢測算法
馬 彬 方 源 謝顯中
1 引言
認(rèn)知無線電(Cognitive Radio, CR)技術(shù)作為一種動(dòng)態(tài)頻譜再利用技術(shù),可以提高稀缺頻譜資源利用率[1,2]。CR中存在兩種用戶,一種是對(duì)頻譜具有絕對(duì)使用權(quán)的主用戶(Primary User, PU),另一種是次用戶(Secondary User, SU)。SU通過主動(dòng)檢測PU頻段,進(jìn)行伺機(jī)接入和退出,因此,SU頻譜檢測的有效性和準(zhǔn)確性是決定能否順利接入頻段重要因素[3]。
傳統(tǒng)頻譜檢測的研究都是假設(shè)在檢測周期內(nèi)PU狀態(tài)不發(fā)生改變,然而,在低信噪比或者高PU業(yè)務(wù)量的場景下,PU的狀態(tài)很可能發(fā)生變化,傳統(tǒng)頻譜檢測技術(shù)的檢測性能會(huì)大大降低[4]。循環(huán)平穩(wěn)特征檢測能夠?qū)⒃肼曅盘?hào)和有用信號(hào)區(qū)分開來,可以擺脫信號(hào)中背景噪聲的干擾[5],在上述情況下有著更好的檢測性能。文獻(xiàn)[6]分析了在PU隨機(jī)離開和到達(dá)兩種情況下的 SU檢測性能,利用平均似然比法則改進(jìn)了傳統(tǒng)能量檢測算法,但在低信噪比場景下的檢測性能并不太理想。文獻(xiàn)[7]和文獻(xiàn)[8]給出了PU狀態(tài)在檢測周期內(nèi)隨機(jī)變化場景下的基于 weight-p能量檢測算法,為采樣樣本賦以單調(diào)增的權(quán)值,較好地區(qū)分了檢測周期內(nèi)不同采樣點(diǎn)位置對(duì)檢測性能的影響。文獻(xiàn)[9]描述了一種基于循環(huán)平穩(wěn)特征檢測的改進(jìn)方法,給出了其二元假設(shè)檢驗(yàn)?zāi)P停⑼ㄟ^廣義似然比準(zhǔn)則推導(dǎo)出了判決統(tǒng)計(jì)量,得到了相比于能量檢測更好的檢測性能,但缺少算法的詳細(xì)理論分析。
本文在查閱相關(guān)資料的基礎(chǔ)上,提出了針對(duì)檢測周期內(nèi)PU隨機(jī)到達(dá)情況下的一種改進(jìn)循環(huán)平穩(wěn)特征檢測算法,由于該算法基于反饋疊加原理,可以在不延長檢測時(shí)間的情況下顯著提高系統(tǒng)的檢測性能。本文的主要貢獻(xiàn)可概括為:
(1)基于反饋疊加原理,增強(qiáng)了用戶隨機(jī)到達(dá)頻譜情況下循環(huán)平穩(wěn)特征檢測算法的檢測準(zhǔn)確性,基于概率論工具詳細(xì)分析了相關(guān)檢測性能。據(jù)作者所知,利用反饋疊加原理來改進(jìn)檢測模型,進(jìn)一步理論分析改進(jìn)后的循環(huán)平穩(wěn)特征檢測算法,還少見報(bào)道。
(2)該文基于改進(jìn)的反饋疊加信號(hào)檢測模型,選取了合適的判決統(tǒng)計(jì)量,把應(yīng)用場景分成兩類,通過有效系數(shù)分別討論了判決統(tǒng)計(jì)量的計(jì)算問題。
2 系統(tǒng)檢測模型
CR網(wǎng)絡(luò)中SU的檢測周期內(nèi),被檢測頻段突然被PU占用情況下的檢測模型可以轉(zhuǎn)化為如式(1)所示的二元假設(shè),其中0H狀態(tài)表示不存在PU,1H狀態(tài)表示存在PU, SU接收到的信號(hào)()x t經(jīng)采樣之后得到式(1)。

其中 Ns表示采樣點(diǎn)數(shù),x[ m]表示SU接收信號(hào),s[ n]表示PU信號(hào), n[ m]表示復(fù)高斯白噪聲信號(hào),其服從均值為0,方差為 δ2的高斯分布。在 H1狀態(tài)中,假設(shè)PU在第n個(gè)采樣時(shí)隙內(nèi)隨機(jī)接入頻譜,且在一個(gè)檢測周期內(nèi)PU最多接入的次數(shù)為一次。
為了提高上述二元假設(shè)模型下的檢測性能,本文提出了一種基于反饋疊加原理的改進(jìn)檢測模型。將檢測周期后半部分采樣點(diǎn)的瞬時(shí)值累加到前半部分采樣點(diǎn)的瞬時(shí)值上,如果在 SU檢測周期的后半部分采樣點(diǎn)中含有用戶信號(hào),那么經(jīng)過反饋累加之后,在檢測周期的前半部分中也將含有用戶信號(hào),從而提高了判決統(tǒng)計(jì)量。新檢測模型如圖1所示,其中灰色表示檢測周期中存在PU信號(hào)的采樣點(diǎn),白色表示檢測周期中不存在PU信號(hào)的采樣點(diǎn)。
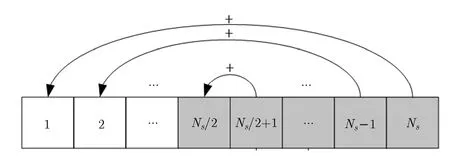
圖1 反饋疊加檢測模型
3 反饋疊加循環(huán)平穩(wěn)特征頻譜檢測算法及性能分析
3.1 傳統(tǒng)循環(huán)平穩(wěn)特征算法
循環(huán)平穩(wěn)信號(hào)是一種統(tǒng)計(jì)特性隨時(shí)間周期性變化的隨機(jī)信號(hào)[10]。設(shè)隨機(jī)過程x( t),如果其均值mx( t) 和自相關(guān)函數(shù) Rx( t) 在一段時(shí)間內(nèi)具有周期性,則稱x( t)廣義循環(huán)平穩(wěn)。由于Rx( t)具有周期特性,可將其展開為傅里葉級(jí)數(shù)形式:

其中 αk= k / T( k = 0 ,1,2,…) 稱為信號(hào)的循環(huán)頻率,k= 0 時(shí),循環(huán)自相關(guān)函數(shù)就是傳統(tǒng)意義上的自相關(guān)函數(shù)。(τ)是傅里葉級(jí)數(shù)的系數(shù),稱為循環(huán)自相關(guān)系數(shù)(Cyclic Autocorrelation Function, CAF),(τ)為
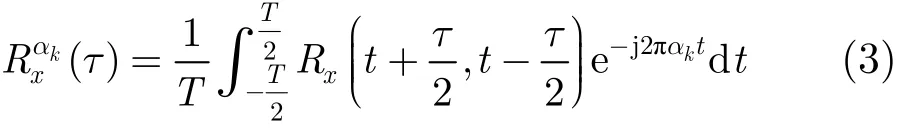
若信號(hào)具有循環(huán)遍歷性,統(tǒng)計(jì)平均可以由時(shí)間平均來代替,有
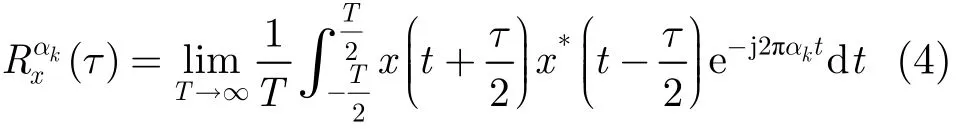
其中,t=mΔt(Δt是采樣周期,m= 1 ,2,…, Ns),T = NsΔt (Ns是采樣數(shù)),對(duì)(τ)求離散形式,得到式(5)
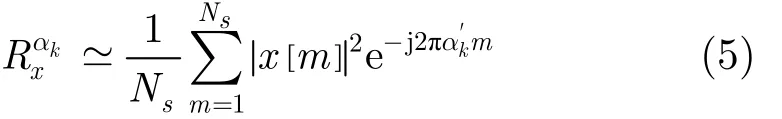
在循環(huán)平穩(wěn)特征檢測中,判決統(tǒng)計(jì)量的選取往往與循環(huán)自相關(guān)系數(shù)有關(guān)。合適的判決統(tǒng)計(jì)量不僅可以顯著減少運(yùn)算量,而且可以實(shí)現(xiàn)更好的檢測性能。通過對(duì)現(xiàn)有文獻(xiàn)的查閱,選擇式(6)所示的判決統(tǒng)計(jì)量[11]:
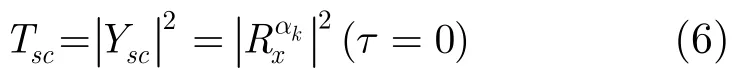
其中,定義scY 為有效系數(shù),有
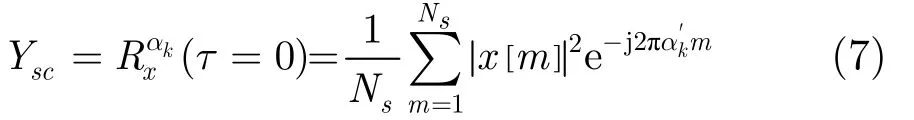
3.2 改進(jìn)循環(huán)平穩(wěn)特征算法分析
在圖1的檢測模型中,用 a(0,1,… ,Ns)表示在檢測周期后半部分含有PU信號(hào)的采樣點(diǎn)數(shù)目,H0條件下 a = 0 ,表示檢測周期中只存在噪聲不存在PU信號(hào); H1條件下 a > 0 ,表示檢測周期中存在 PU信號(hào)。下面分別對(duì) H0和 H1情況下的有效系數(shù)進(jìn)行討論。
H0條件下 a = 0 , SU的檢測周期中只存在噪聲,不存在PU信號(hào),對(duì)信號(hào)采樣值反饋疊加后如圖2所示。
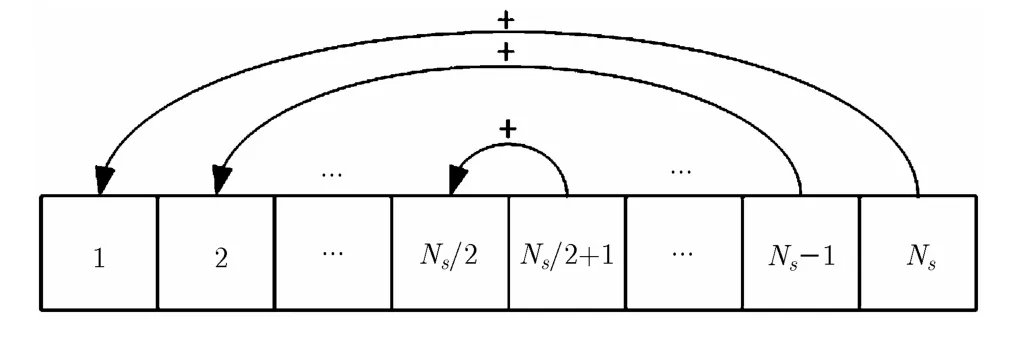
圖2 0H 條件下檢測周期
根據(jù)式(7)計(jì)算 H0條件下有效系數(shù) Ysc:
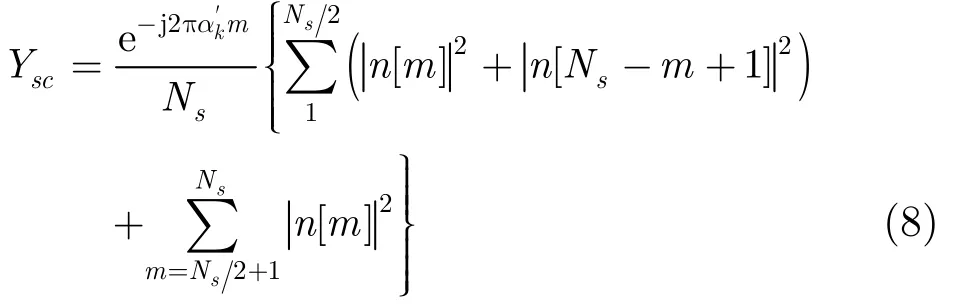
在 H1條件下,當(dāng)檢測周期內(nèi)主用戶突然出現(xiàn)時(shí),對(duì)有效系數(shù)進(jìn)行分析,但是要對(duì)a值的大小分兩種情況進(jìn)行討論。
第1種情況:PU于檢測周期中后段時(shí)間到達(dá)
當(dāng)0 < a ≤ Ns/2時(shí),PU于檢測周期中后段某個(gè)時(shí)隙到達(dá),對(duì)接收端信號(hào)采樣值反饋疊加后如圖 3所示。
根據(jù)式(7)計(jì)算該條件下有效系數(shù) Ysc:

第2種情況:PU于檢測周期前段時(shí)間到達(dá)
當(dāng) Ns/2< a ≤ Ns時(shí),PU于檢測周期前段某個(gè)時(shí)隙到達(dá),對(duì)接收端信號(hào)采樣值反饋疊加后如圖4所示。
根據(jù)式(7)計(jì)算該條件下有效系數(shù) Ysc:
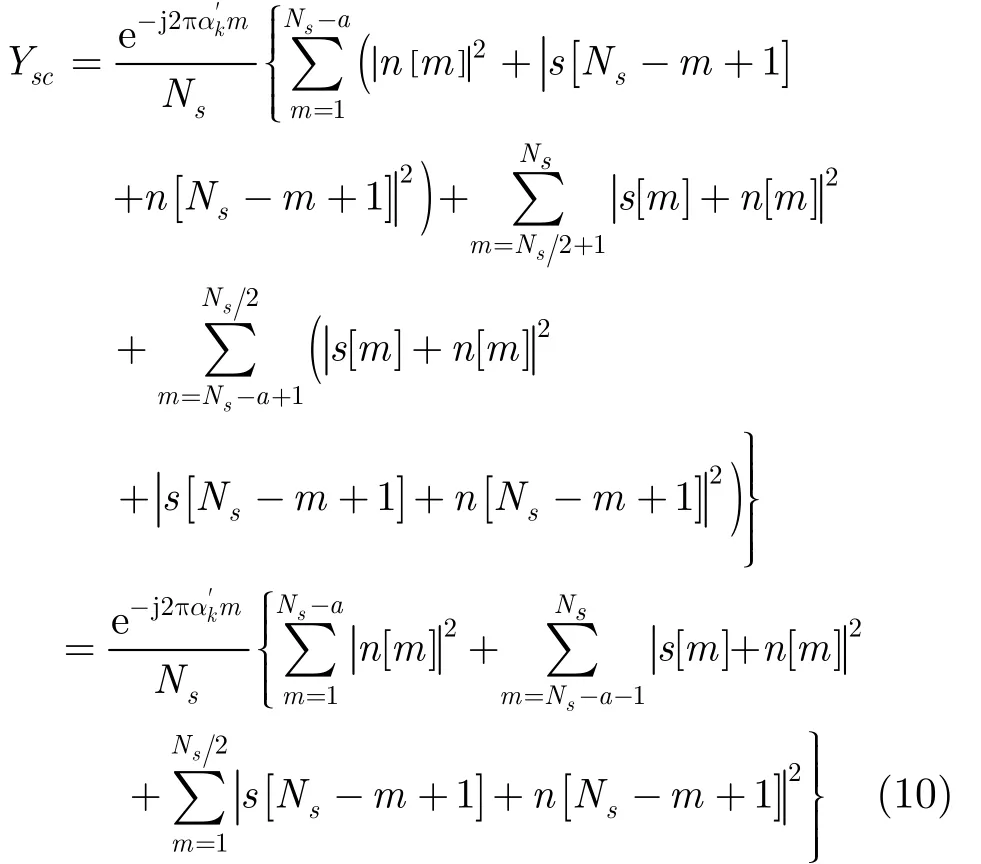
特別地,當(dāng) a = Ns時(shí),檢測周期中全部存在用戶信號(hào),根據(jù)式(8)計(jì)算該條件下有效系數(shù) Ysc:
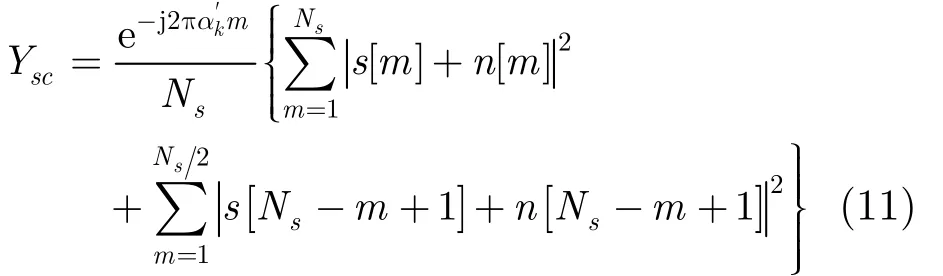
3.3 性能分析
3.3.1 虛警概率和檢測概率分析 二元假設(shè)檢驗(yàn)?zāi)P拖碌臋z測概率和虛警概率如式(12)所示,其中scT 為判決統(tǒng)計(jì)量。
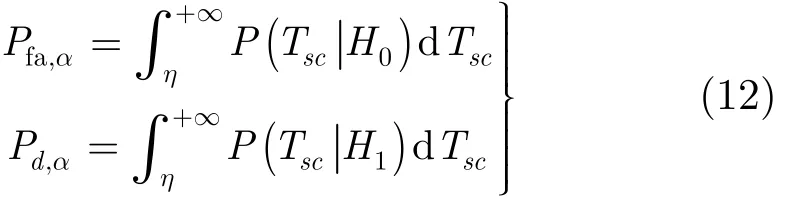
假設(shè)噪聲n( t)是服從均值為0,方差為σ2的復(fù)高斯白噪聲,即 n[ m ]= n [ m ]+ jn[ m ]。存在E{n[ m]2}
r i= σ2,var{n[ m ]2}=var{n [ m ]2+n [ m ]2} =σ4。假設(shè)
r i信號(hào)s( t) 與噪聲n( t)相互獨(dú)立,則E{s[ m ]+ m [ m]2}= s[ m ]2+ σ2。

圖3 H 1中0 < a ≤ N s/2條件下檢測周期

圖4 H 1中 N s/ 2< a ≤ N s條件下檢測周期
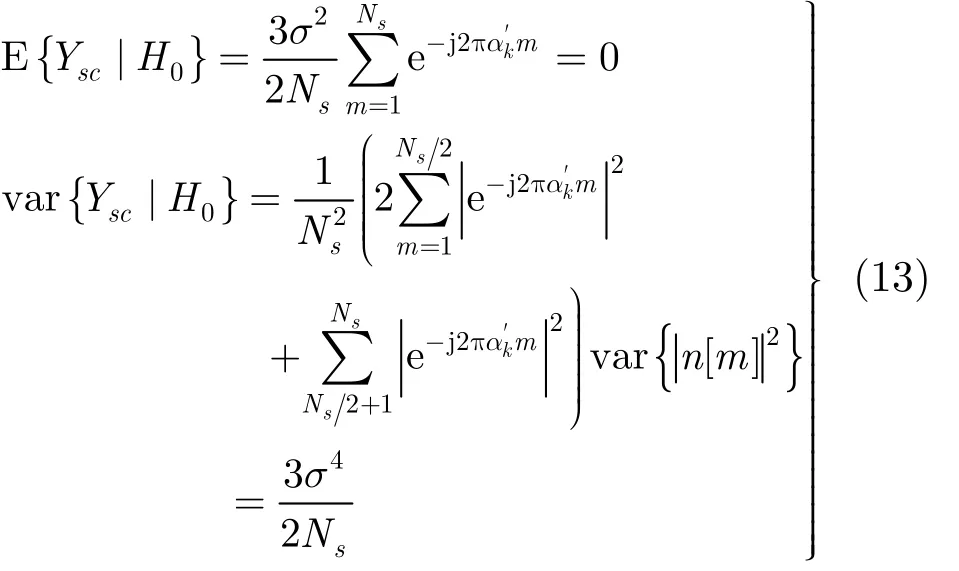
由于(T |H )=(Y |H )2= ( Yr)2+ (Yi)2,所
sc 0sc000以(Tsc|H0)服從自由度為2的中心卡方分布,根據(jù)中心卡方分布的概率密度函數(shù)公式,得到 P ( Tsc|H0)

根據(jù)式(12)對(duì) P ( T sc |H0) 積分,得到虛警概率

其中η是判決門限。在實(shí)際的檢測環(huán)境中,為滿足一定的檢測性能,需要設(shè)定目標(biāo)虛警概率,根據(jù)式(15)可以得到條件下反饋疊加循環(huán)平穩(wěn)特征算法的判決門限 η =-3 σ4ln。
H1條件下根據(jù)PU到達(dá)時(shí)間的不同分兩種情況對(duì)檢測概率進(jìn)行分析。
第1種情況:PU于檢測周期中后段時(shí)間到達(dá)
當(dāng)0 < a ≤ Ns/2時(shí),根據(jù)中心極限定理,如果Ns? 1 ,那么 Ysc近似服從高斯過程,根據(jù)式(9)計(jì)算其分布的均值和方差。
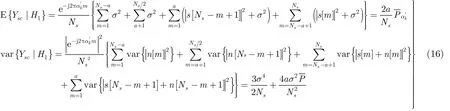
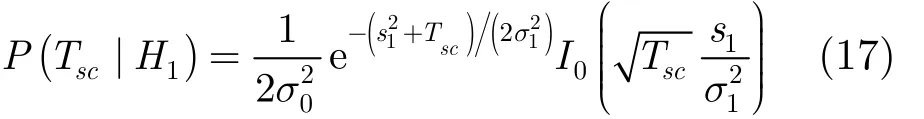
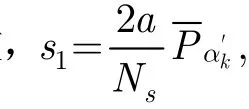
根據(jù)式(12)對(duì) P ( Tsc|H1) 積分得檢測概率:

其中Q1( a, b)一階伽瑪函數(shù)。
第2種情況:PU于檢測周期前段時(shí)間到達(dá)
當(dāng) Ns/2 <a≤Ns 時(shí),根據(jù)中心極限定理,如果 Ns? 1 ,那么 Ysc近似服從高斯過程,根據(jù)式(10)計(jì)算其分布均值和方差。
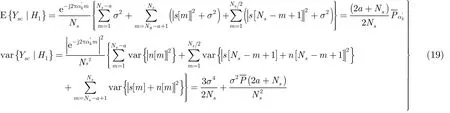
同理式(18),得 Ns/2<a≤Ns情況下檢測概率:
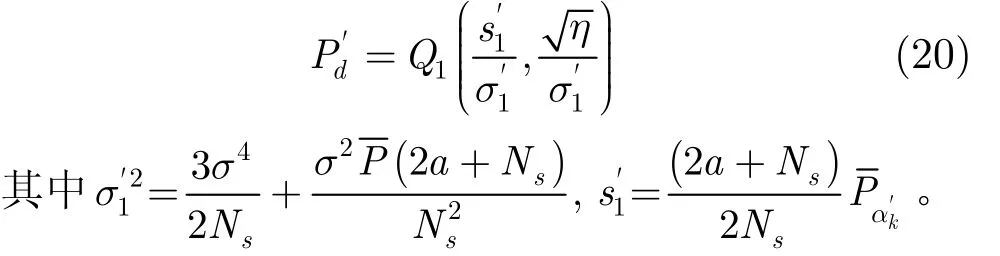
3.3.2 吞吐量分析 在SU檢測周期內(nèi)PU的突然出現(xiàn),導(dǎo)致SU檢測周期內(nèi)前半部分只含有AWGN信號(hào),后半部分含有的是PU信號(hào)和AWGN信號(hào)的混合信號(hào)[12],如圖5所示。圖5中,SU在執(zhí)行頻譜檢測過程中,PU突然出現(xiàn),增大了發(fā)生碰撞的概率從而對(duì)SU吞吐量產(chǎn)生影響。
假設(shè)CR網(wǎng)絡(luò)中PU到達(dá)概率服從泊松分布,那么用戶之間到達(dá)網(wǎng)絡(luò)的時(shí)間間隔服從指數(shù)分布f (τ) =, τ >0,其中λ 為用戶業(yè)務(wù)量強(qiáng)度或a者稱之為到達(dá)率,τ0為采樣時(shí)間。那么在圖5的模型下,CR網(wǎng)絡(luò)中數(shù)據(jù)傳輸發(fā)生碰撞的平均概率如式(21)所示。

相應(yīng)可以得到SU歸一化的數(shù)據(jù)平均吞吐量。

其中fraT 為SU傳輸數(shù)據(jù)幀長度,sensT 為檢測時(shí)間。
4 仿真分析

圖5 SU檢測周期內(nèi)PU出現(xiàn)對(duì)吞吐量的影響
設(shè)用戶信號(hào)采用BPSK調(diào)制,工作在電視頻譜頻段,載波頻率為500 MHz,采樣頻率為6 MHz,碼率為100 bps。CR的目標(biāo)虛警概率為0.1,目標(biāo)檢測概率為0.98。用戶到達(dá)網(wǎng)絡(luò)服從泊松分布,利用MATLAB進(jìn)行仿真比較。
4.1 檢測概率分析
4.2 虛警概率分析
4.3 采樣點(diǎn)數(shù)分析
4.4 吞吐量分析
圖10表示SU業(yè)務(wù)量強(qiáng)度aλ=50, SNR=-20 dB時(shí),SU數(shù)據(jù)吞吐量隨數(shù)據(jù)幀長度變化的情況。圖10中,隨著SU數(shù)據(jù)幀長度增大,數(shù)據(jù)吞吐量首先提高,當(dāng)sens=400 ms
T時(shí),SU數(shù)據(jù)吞吐量趨于不變。這是由于數(shù)據(jù)碰撞概率隨 SU數(shù)據(jù)幀長度的增大而增大,但是增大到飽和狀態(tài)時(shí),吞吐量將不再受數(shù)據(jù)幀長度的影響。圖11表示aλ=50,sens=400 ms T時(shí),SU數(shù)據(jù)吞吐量隨目標(biāo)檢測概率的變化情況。圖11中,隨著目標(biāo)檢測概率的提高,ED的SU數(shù)據(jù)吞吐量有所下降,原因是提高導(dǎo)致數(shù)據(jù)碰撞概率提高,從而使SU獲得的數(shù)據(jù)吞吐量下降。圖10和圖11中,F(xiàn)A-CFD的SU數(shù)據(jù)吞吐量歸一化峰值和CFD基本相同,達(dá)到0.9左右,ED的為0.5左右,表明FA-CFD和CFD相對(duì)于ED有著不錯(cuò)的數(shù)據(jù)吞吐量表現(xiàn)。
5 結(jié)束語
該文提出了一種基于反饋疊加原理的改進(jìn)循環(huán)平穩(wěn)特征檢測算法,提高了檢測周期內(nèi)PU狀態(tài)隨機(jī)變化情況下的檢測性能。所提出的改進(jìn)算法相對(duì)于傳統(tǒng)的循環(huán)平穩(wěn)特征檢測和能量檢測有著更好的檢測性能,相對(duì)于傳統(tǒng)的循環(huán)平穩(wěn)特征檢測需要更少采樣點(diǎn)數(shù)的同時(shí)保證了較高的數(shù)據(jù)吞吐量,但是,也可以看出該改進(jìn)算法也存在著虛警概率偏大,運(yùn)算復(fù)雜度高等問題。下一步工作將繼續(xù)研究頻譜檢測優(yōu)化問題,并嘗試將其應(yīng)用于對(duì)檢測性能要求高的CR安全領(lǐng)域。
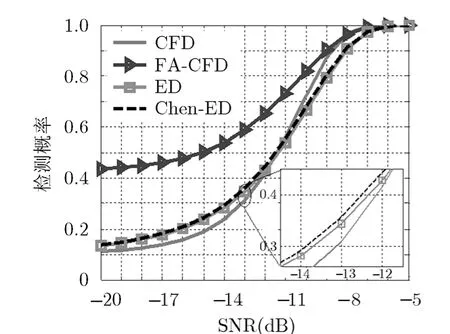
圖6 4種檢測方法檢測概率對(duì)比曲線
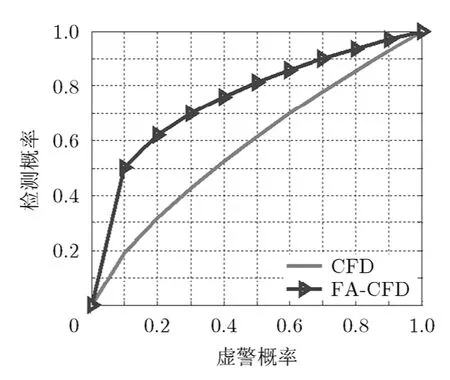
圖7 SNR=-15dB情況下ROC曲線
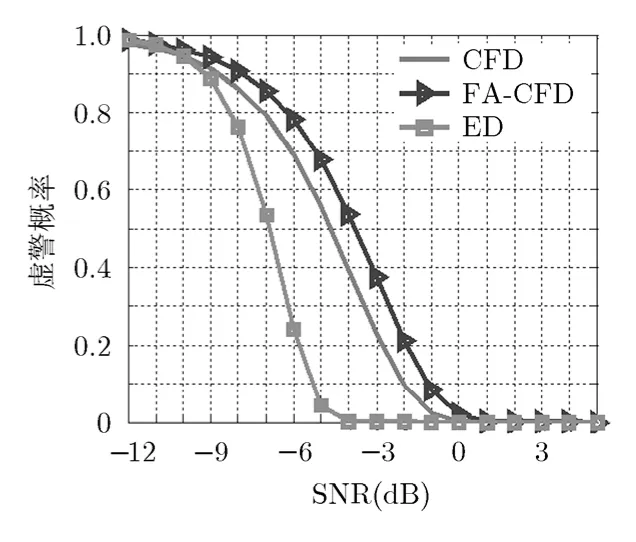
圖8 3種檢測方法虛警概率對(duì)比曲線
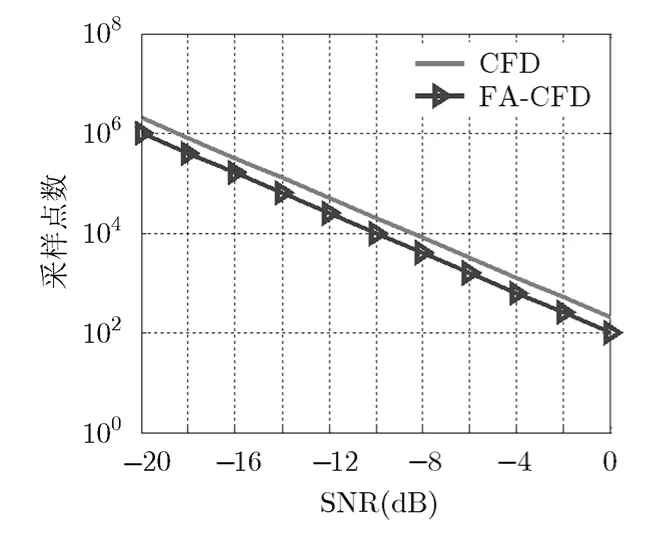
圖9 改進(jìn)前后采樣點(diǎn)數(shù)對(duì)比
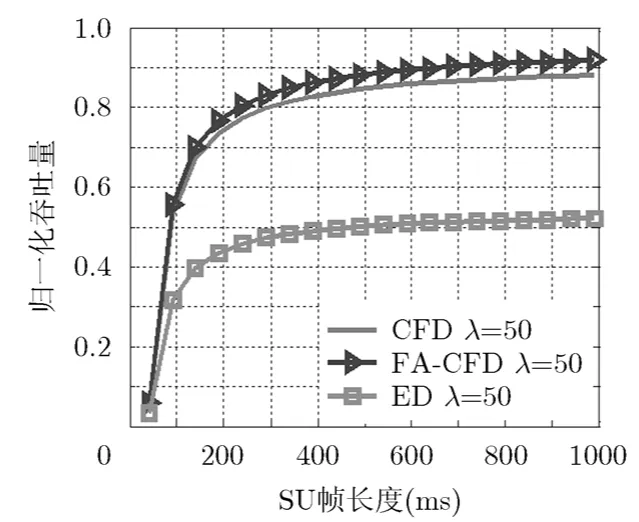
圖10 SU吞吐量隨數(shù)據(jù)幀長度的變化
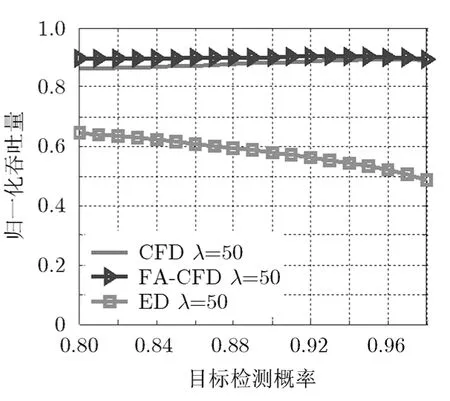
圖11 SU數(shù)據(jù)吞吐量隨 的變化
[1] Ma Bin, Xie Xian-zhong, and Liao Xiao-feng. An efficient proactive spectrum handover mechanism in cognitive radio networks[J]. Wireless Personal Communications, 2014, 79(3):1679-1701.
[2] Wilcox D, Tsakalaki E, Kortun A, et al.. On spatial domain cognitive radio using single radio parasitic antenna arrays[J].IEEE Journal on Selected Areas in Communications, 2013,31(3): 571-580.
[3] Yucek T, Huseyin, and Arslan. A survey of spectrum sensing algorithms for cognitive radio applications[J]. IEEE Communications Surveys & Tutorials, 2009, 11(1): 116-130.
[4] Wang T, Chen Y, Zhao B, et al.. Analysis of effect of primary user traffic on spectrum sensing performance [C]. Proceedings of the IEEE China fourth international conference on communications and networking (ChinaCOM2009), Xi,an,China, 2009: 1-5.
[5] Mohapatra S G, Mohapatra A G, and Lenka S K.Performance evaluation of cyclostationary based spectrum sensing in cognitive radio network[C]. Proceedings of the IEEE 2013 International Multi-Conference on Automation,Computing, Communication, Control and Compressed Sensing (iMac4s), Kottayam, India, 2013: 90-97.
[6] Beaulieu N C and Chen Y. Improved energy detectors for cognitive radios with randomly arriving or departing primary users[J]. IEEE Signal Processing Letters, 2010, 17(10):867-870.
[7] 謝顯中, 胡小峰, 馬彬, 等. 主用戶狀態(tài)改變和低信噪比環(huán)境下的 weight-p能量檢測法[J]. 中國科學(xué): 信息科學(xué), 2014,44(4): 537-550.Xie Xian-zhong, Hu Xiao-feng, Ma Bin, et al.. A new weight-p energy detector for primary user status changes and low SNR environments[J]. SEIENCE CHINA Information Sciences,2014, 44(4): 537-550.
[8] Xie Xian-zhong, Hu Xiao-feng, Ma Bin, et al.. Improved energy detector with weights for primary user status changes in cognitive radio networks[J]. International Journal of Distributed Sensor Networks, 2014,doi:10.1155/2014/836793.
[9] Shim J, Lee J, Lee Y, et al.. A cyclostationary spectrum sensing scheme for high traffic environments[C]. Proceedings of the 2013 3rd International Conference on Wireless Communications, Vehicular Technology, Information Theory and Aerospace & Electronic Systems (VITAE), Atlantic City,NJ, USA, 2013: 1-4.
[10] Gardner W A. Introduction To Random Processes[M]. USA:McGraw- Hill, 1986: 323-346.
[11] Gardner W A and Spooner M S. Signal interception:performance advantages of cyclic-feature detectors[J]. IEEE Transactions on Communications, 1992, 40(1): 149-159.
[12] Liang T, Chen Y, Hines E L, et al.. Effect of primary user traffic on sensing-throughput tradeoff for cognitive radios [J].IEEE Transactions on Wireless Communications, 2011, 10(4):1063-1068.
[13] Masoumeh D, Masoumeh N K, and Tho L N. Cooperative cyclostationary spectrum sensing in cognitive radios at low SNR regimes[C]. Proceedings of the IEEEInternational Conference on Communications (ICC), Cape Town, Republic of South Africa, 2010: 1-5.
[14] Tandra R and Sahai A. SNR walls for signal detection[J].IEEE Journal of Selected Topics in Signal Processing, 2008,2(1): 4-17.
[15] Chen Y F. Improved energy detector for random signals in Gaussian noise[J]. IEEE Transactions on Wireless Communications, 2010, 9(2): 558-563.

