雙向中繼系統(tǒng)用戶聯合預編碼與檢測算法研究

王 林 芮國勝 張海波

1 引言

中繼協同通信技術由于其潛在的高速率、大容量、抗衰落、覆蓋范圍廣等優(yōu)勢受到廣泛關注，目前已成為重要的研究熱點[13]-。為了彌補單向中繼在半雙工通信模式下，提高邊緣用戶性能的同時，浪費時隙資源造成頻譜效率的損失，Rankov等人[4]提出了放大轉發(fā)（Amplify-and-Forward, AF）和解碼轉發(fā)（Decode-and-Forward, DF）協議下的雙向中繼機制，雙向中繼的兩個用戶節(jié)點可以同時向中繼節(jié)點發(fā)射信號，兩個時隙資源之內即可完成一次信息交互，有效地提高了系統(tǒng)的頻譜效率[5]，并且用戶總速率也比單向中繼系統(tǒng)更高。

當雙向中繼協同通信系統(tǒng)中的節(jié)點安裝了多根天線時，中繼協同技術就可以和MIMO系統(tǒng)常用的預編碼及檢測技術結合起來[6]。中繼協同系統(tǒng)中的空間自由度就可以用來提高鏈路可靠性，并且在已知信道狀態(tài)信息（CSI）的情況下，能夠通過預編碼操作提升系統(tǒng)的整體性能。文獻[7]針對單向中繼系統(tǒng)總結了放大轉發(fā)模式下系統(tǒng)的優(yōu)化算法和預編碼設計方法。文獻[8]針對存在直連鏈路的單向中繼系統(tǒng)，給出了基于最小均方誤差的預編碼矩陣的閉式解，并對中斷性能進行了研究。而對于多天線雙向中繼系統(tǒng)來說，信號處理比較復雜，現有針對雙向中繼協同通信的預編碼設計大都基于線性預編碼方式，如文獻[9]針對雙向系統(tǒng)在延時和有限反饋的信道信息情況下的中繼預編碼矩陣進行分析，文獻[10]利用迭代方式將用戶預編碼與中繼預編碼相結合，得到聯合預編碼矩陣。然而在無線通信系統(tǒng)中，上述方案采用的線性預編碼方法原理簡單、復雜度低，但也存在著容量較低，很難實現系統(tǒng)大容量高速率。而非線性預編碼在容量及誤碼率方面則具有較大優(yōu)勢，特別是其中被廣泛應用的模代數預編碼（Tomlinson-Harashima Precoding, THP）相比原始的臟紙編碼復雜度大大降低，易于工程實現[11]。但是THP算法在處理實際的信道矩陣時，由于信道正交性不好，性能會受到較大的影響。針對此問題，根據雙向多天線中繼協同通信系統(tǒng)特點，本文提出了一種基于部分信道信息的用戶聯合預編碼與檢測算法，利用在 MIMO信號檢測上常用的格規(guī)約技術[12]（Lattice Reduction, LR）對實際信道矩陣進行正交處理，將預編碼算法應用于用戶節(jié)點發(fā)射信號的多址階段，并利用 LR預處理后的矩陣，將檢測算法應用于用戶節(jié)點接收信號的廣播階段，在系統(tǒng)復雜度增加不大、中繼節(jié)點復雜度較低的情況下，使系統(tǒng)誤比特率得到大幅降低。

2 系統(tǒng)模型

2.1 雙向中繼協同通信系統(tǒng)

考慮如圖1所示的多天線雙向中繼協同通信系統(tǒng)傳輸模型，3個節(jié)點單元均配置多天線且工作在半雙工模式。兩個用戶節(jié)點A與B通過中繼節(jié)點R互相交換信息，并假設兩用戶節(jié)點間沒有直達鏈路，中繼節(jié)點轉發(fā)為AF模式。兩個用戶節(jié)點A與B裝備天線數為N，中繼節(jié)點R的天線數為M，并且為保證用戶間可以傳輸 N 條數據流信息[10]，則可得（M ≥N≥2）。根據信道的互易性，從節(jié)點A到中繼節(jié)點 R的信道增益矩陣為H，而從中繼節(jié)點 R到節(jié)點A的信道增益矩陣為 HT；從節(jié)點B到中繼節(jié)點R的信道增益矩陣為G，而從中繼節(jié)點R到節(jié)點 B的信道增益矩陣為 GT；所有信道均為獨立同分布的慢衰落的Rayleigh信道。所有節(jié)點僅已知其相鄰信道的增益矩陣，即節(jié)點 A已知H，節(jié)點 B已知G，中繼節(jié)點R已知其前后信道的信道增益H與G。

整個傳輸過程分兩個時隙完成，在第1個時隙內（多址階段），兩用戶節(jié)點A與B同時將各自信息xA與 xB發(fā)往中繼節(jié)點R，此時中繼節(jié)點R接收到的信號為

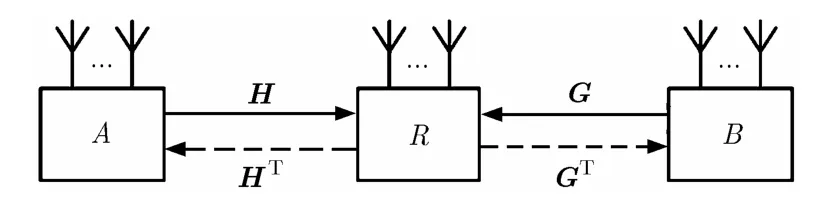
圖1 多天線雙向中繼系統(tǒng)傳輸模型

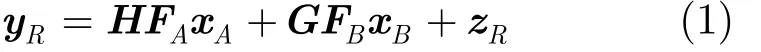
其中，H, G ∈ ?M×N為信道矩陣， Fm代表用戶節(jié)點m的預編碼矩陣，=[,… ,]T為用戶節(jié)點m的發(fā)射信號，上述表達式中 m ∈{A, B}。zR表示零均值方差為的加性復高斯白噪聲。用戶m的最大發(fā)射功率限定為Pm，將每個數據流信息進行歸一化，即矩陣協方差滿足：

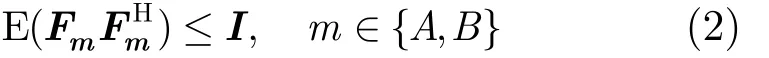
因此，兩用戶節(jié)點的功率限制可寫為

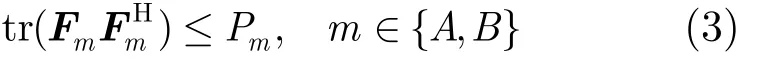
中繼節(jié)點接收到信號Ry后，通過求模運算和放大后，可以得到新的信號：

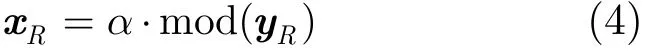
式中，α為放大因子，由于中繼節(jié)點R的最大發(fā)送功率限制為PR，所以α的值有如下限制：

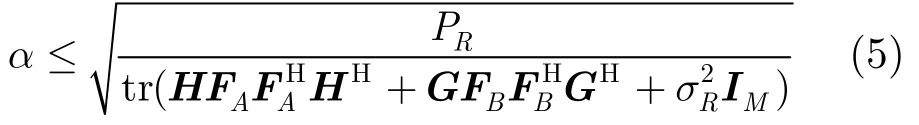
在第2個時隙內（廣播階段），中繼節(jié)點將xR廣播到兩個用戶節(jié)點，兩用戶節(jié)點接收到的信號分別為

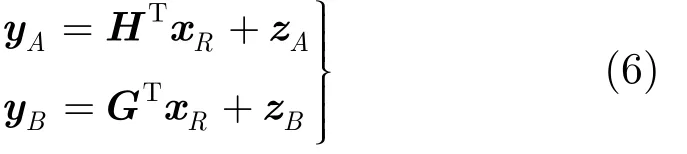
式（6）的信號傳輸可以看做點到點的 MIMO 信道，所以可以用現有的檢測算法對其進行檢測。在用戶節(jié)點A和B處，可分別應用復雜度較低的迫零（Zero Forcing, ZF）檢測算法，則可得均衡濾波器矩陣為?n×m，進一步可以得到

由于用戶節(jié)點A和B已知各自的發(fā)送的信息，可以根據自干擾消除的原理，得到對方發(fā)送的有用信息為

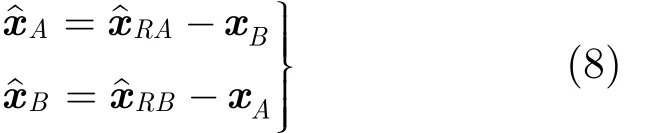
2.2 復數域格歸約

格規(guī)約算法的實質就是通過變換得到新的信道增益矩陣，相對于原始信道增益矩陣H和G，新矩陣的正交性更好，向量長度更短[13]。在n維復空間Cn中定義秩為m的復數值的格[12]。

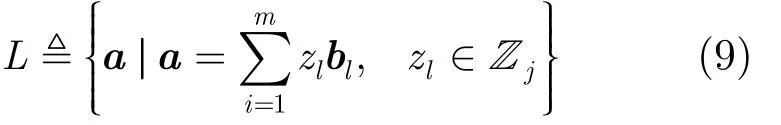
目前，LLL 規(guī)約算法與其他的格規(guī)約算法相比，在相同性能下，以加法和乘法次數為參考標準的算法復雜度最低，因此在MIMO系統(tǒng)中得到了廣泛的應用[14]。復數域的LLL算法簡稱CLLL算法，相比于實數域的LLL算法，其算法的計算復雜度可以降低50%以上[15]。所以，本文采用文獻[12]給出的基于QR分解的CLLL算法對雙向的信道增益矩陣進行預處理。

3 預編碼和檢測設計

3.1 LR-THP預編碼

本節(jié)對兩用戶節(jié)點A與B的相鄰信道增益矩陣設計預編碼矩陣AF和BF。如前文所述，THP預編碼在MIMO系統(tǒng)中得到了廣泛應用，傳統(tǒng)的THP預編碼結構如圖2所示。

圖2中，F為發(fā)送端的前向反饋預編碼矩陣，由于F是酉矩陣，因此不會改變a~的功率。B-I是一個對角元素為1的下三角矩陣，用來消除因果干擾。在發(fā)射端，調制信號a經過B-I以及求模運算，產生編碼后的符號a~，然后經過加權矩陣U和預編碼矩陣 F，以消除信道影響。接收端只需再經過一次的求模運算就可以恢復出原始的信號。

對于THP預編碼矩陣的求解有多種方法，以常用的QR分解為例，結合ZF準則對信道增益矩陣H進行處理。

式（10）中S為下三角矩陣，圖2中的加權矩陣U可表示為

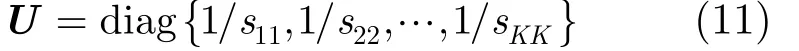
這里 skk是S對角線中的元素， k =1,2,… ,K，并且 K =min（Nt, Nr）。基于QR分解和ZF準則下的THP預編碼算法可總結為

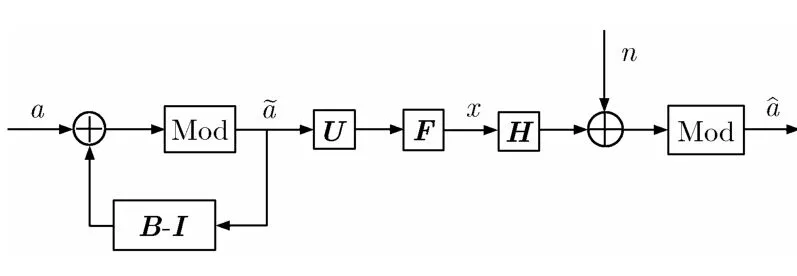
圖2 傳統(tǒng)THP算法結構圖

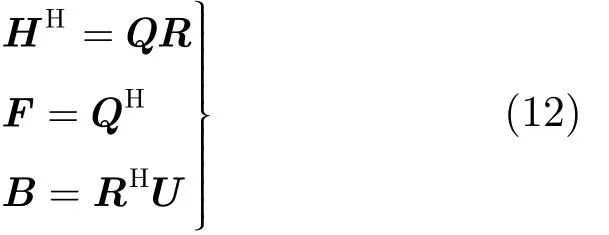
式中Q為Nt×K階矩陣，并且有QQH=I,R為具有對角線元素為{rii}的K×K階上三角矩陣。

根據格規(guī)約理論，LR算法對信道增益矩陣進行預處理，使其正交性更好，向量長度更短。對雙向中繼協同通信系統(tǒng)的信道增益矩陣進行轉置，并應用CLLL算法，可以得到處理后的新矩陣：

式中Tm,m ∈ { A, B}為復數單模矩陣，且 Tm的行列式的值為1或±j。對式（13）左右兩邊同時轉置則可進一步寫為

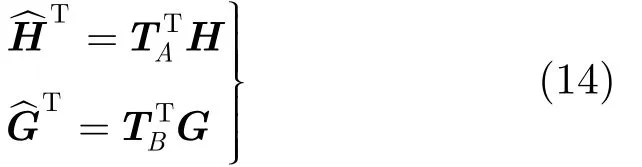
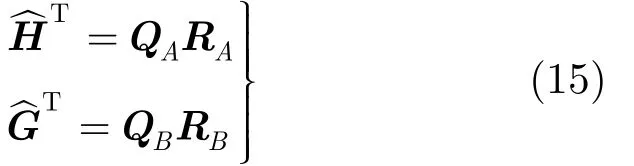
式中，Qm是一個N×M階的列正交矩陣，Rm為M×M階的上三角矩陣，其對角線上元素為復數{}。根據THP預編碼算法的結構，可以得到雙向中繼系統(tǒng)的預編碼矩陣。

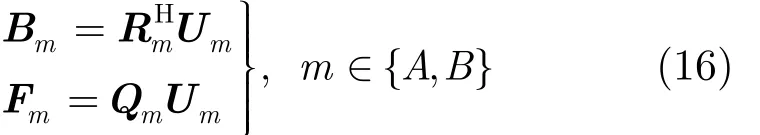
式中mB 為后置濾波器反饋矩陣，相當于圖 2中的B-I,mF 為預編碼矩陣，相當于圖2中的F。mU 為對角陣，其值為mR 對角線元素的倒數，即

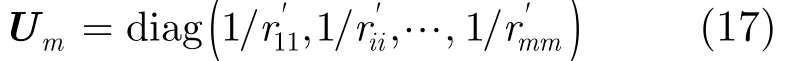
在中繼節(jié)點R處，接收到兩個用戶的混合信號，只需要一步求模運算，便可以得到接收信號。

3.2 LR-ZF檢測

由式（4）可知，中繼節(jié)點 R接收到信號Ry 后，通過求模和放大后，可以得到新的信號Rx。中繼節(jié)點R廣播Rx到兩用戶節(jié)點，這相當于一個多用戶的MIMO信道。用戶節(jié)點的檢測算法較多，基于最大似然準則（Maximum Likelihood, ML）的檢測算法是誤比特率意義上的最優(yōu)算法，但是其復雜度很高，并隨著調制階數和發(fā)射天線的增加，呈指數形式增長，在實際通信中很難實現[16]。ZF檢測器的算法復雜度較低，但是引入了其他層噪聲干擾，無法獲得全分集增益最終影響了檢測性能。所以實用的檢測算法需要在算法復雜度和檢測性能間找到合理的平衡。所以雙向中繼系統(tǒng)的用戶節(jié)點需采用LR-ZF檢測算法。該檢測算法由于經過 LR算法對矩陣進行預處理，增強了矩陣列向量的正交性，減小了其它層的干擾，檢測性能大大提高。并且由于在預編碼中已經對矩陣進行了 LR處理，所以其復雜度相比傳統(tǒng)ZF算法增加很小。

由式（13）可知，信道增益矩陣的轉置 HT和GT經過CLLL算法預處理后的矩陣分別為和，式（7）中的指零矩陣WA和WB可以表示為

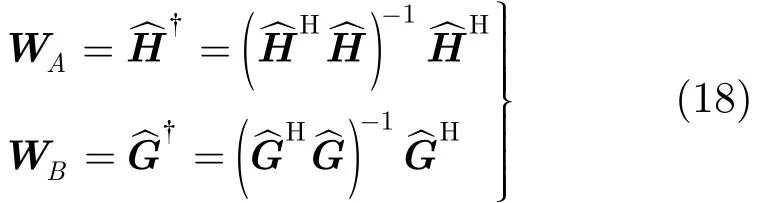
然后通過式（19）可以得到信號矩陣RAS 和RBS ，這里的信號矩陣是中繼發(fā)送的信號通過處理后的信道增益矩陣得到的。

此時信號矩陣 SRA和 SRB相對于式（7）中的 x?RA和發(fā)生了變換，所以需要通過式（20）的變換關系，得到原始的信號。

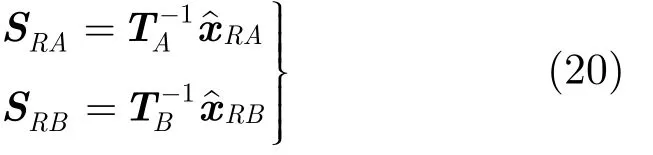
從式（20）得出RAx? 和RBx? 后，用戶節(jié)點 A 和 B 可以根據已知信息，通過式（8）中的自干擾消除得到對方發(fā)送的信息。

3.3 算法總結

綜上所述，雙向中繼協同通信系統(tǒng)的用戶聯合預編碼與檢測算法的原理，可以表示為圖3所示結構框圖。

在圖3中，Rz為加性噪聲，Mod模塊代表求模運算，用來降低峰值或者平均功率，這是一個非線性的過程。結合框圖及以上兩節(jié)對預編碼與檢測算法的描述，現將算法步驟歸納如下：

步驟 1 首先通過CLLL算法對信道增益矩陣進行預處理，如式（13）所示，得到處理后的信道增益矩陣和。

步驟3 兩節(jié)點用戶的發(fā)送信息 xA與 xB，通過圖3所示流程圖發(fā)往中繼節(jié)點R，中繼節(jié)點接收到信號 yR后，如式（4）所示通過求模運算和放大后，可以得到新的信號 xR。

步驟4 通過式（18）計算得到 LR-ZF檢測算法的指零矩陣 WA和WB。

步驟5 根據式（19），式（20），兩用戶節(jié)點可進一步得到 x?RA和 x?RB，通過式（8）中自干擾消除的方法，就可得到對方發(fā)送的信息。

4 復雜度分析

第 3節(jié)中提出的算法是在復數域下進行討論的，因此計算復雜度以所需的復數加法和復數乘法次數之和為依據。

3.3 節(jié)中步驟1中式（13）的計算復雜度取決于用CLLL算法所需復數運算次數。CLLL算法運算次數并不是一個定值，文獻[15]給出了CLLL算法的復雜度只是所需復數加乘運算次數的一個“上界”。則式（13）的計算復雜度可表示為

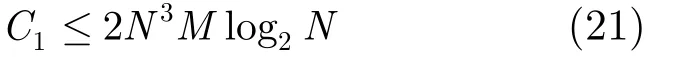
需要指出式（21）給出的理論值遠大于實際所需的復數計算次數。只有當信道矩陣的條件數很大時，理論計算值才與算法實際復數計算次數相近。

步驟2中QR分解所需要的復雜度[17]為

步驟3中的求模和放大運算需要的計算復雜度很小，并且傳統(tǒng)的THP預編碼算法都存在，本文不對其進行討論。

步驟4中計算式（18）中的指零矩陣AW 和BW 需要的復數加法次數為

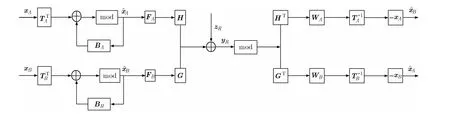
圖3 雙向中繼協同通信系統(tǒng)的LR-THP結構圖

需要的復數乘法次數為

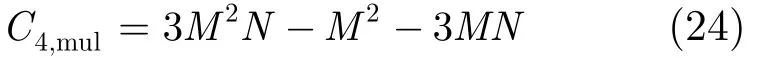
所以，步驟4所需要的復數加乘和為

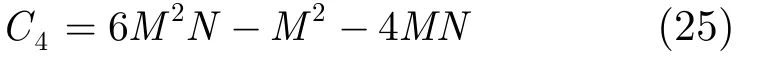
步驟5中對式（19）的計算，需要2MN次復數乘法運算以及 2 M （ N - 1 ）次復數加法運算。式（20）需要2N2次復數乘法運算以及 2 N （ N - 1 ）次復數加法運算。式（8）需要2MN復數加法運算。所以步驟 5需要復雜度為

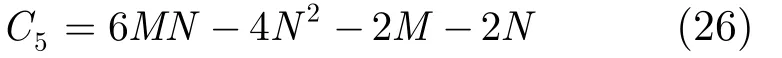
綜合以上部分的復雜度相加，就是本文所提聯合預編碼和檢測算法的計算復雜度。可得算法復雜度

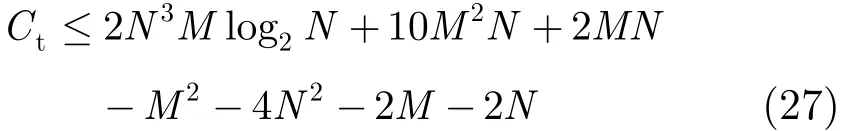
從式（27）中可以看出，本文的算法復雜度為3N數量級，對比傳統(tǒng)的THP預編碼算法，以及ZF檢測算法可知，本文算法復雜度并沒有數量級上的增加，主要是中繼節(jié)點兩側信道各一次的CLLL算法部分的增加了復雜度，對于當前的硬件計算能力，是可以接受的。

5 仿真結果與性能分析

為了說明本文算法的優(yōu)越性，采用Matlab數值仿真的方式，對其的誤比特率（Bit Error Rate, BER）性能進行驗證。首先給出了本文LR-THP預編碼算法與以下3種情況的誤比特率性能曲線對比：傳統(tǒng)的MMSE準則下的THP預編碼算法，以THP表示；格規(guī)約輔助的ZF預編碼算法，即LR-ZF預編碼算法；未進行預編碼操作的 AF雙向中繼協同通信，以AF表示。然后給出了本文檢測算法與傳統(tǒng)的ZF準則和MMSE準則下檢測算法誤比特率性能的對比。

設置仿真實驗場景為典型的多天線雙向中繼系統(tǒng)傳輸模型，假設所有節(jié)點都有 4根天線，即M = N = 4 ，并且3個節(jié)點的發(fā)射功率相同。所有信道是獨立同分布平坦衰落的復高斯隨機信道，并且在各節(jié)點可以獲得相鄰信道的完整信道狀態(tài)信息。調制方式采用正交幅度調制，分別以4QAM和16QAM為例。

為了便于公平比較所有的預編碼算法，在兩用戶節(jié)點都采用了本文提出的檢測算法在接收端計算誤碼率。在4QAM調制方式的雙向中繼系統(tǒng)下，各預編碼算法的性能曲線如圖4所示，從圖4中可以看出，LR-THP算法的誤碼率性能明顯優(yōu)于其他 3種算法，當誤碼率為 1 0-3時，相比于傳統(tǒng)的THP算法，LR-THP算法所需的信噪比降低了9 dB；當誤碼率為 1 0-4時，相比于LR-ZF算法，LR-THP算法所需的信噪比降低了2 dB。并且從圖4中還可以看出，傳統(tǒng)的THP預編碼算法的誤碼率性能比LR-ZF算法還要差，這說明了格規(guī)約算法使信道增益矩陣列向量更短，正交性更好，能夠大幅度提高系統(tǒng)的誤碼率性能。

圖5給出了16QAM調制方式下各預編碼算法的性能曲線，從圖 5中依然可以得出，本文的ZF-THP算法在圖中所有4種方案中誤碼率性能最好。對于16QAM調制方式的雙向中繼系統(tǒng)，當誤碼率為 1 0-3時，相比于傳統(tǒng)的THP算法，LR-THP算法所需的信噪比降低了8 dB；當誤碼率為 1 0-4時，相比于LR-ZF預編碼算法，LR-THP算法所需的信噪比降低了1.5 dB。除此以外，從圖4和圖5中還可以看出，AF方案與其他預編碼方案相比，誤比特率性能最差，這是由于沒有使用預編碼方案使得在中繼節(jié)點R處接收信噪比較低，并且在中繼節(jié)點處對噪聲進行了放大。LR-THP算法的性能最好是由于結合了THP算法與格規(guī)約算法的優(yōu)點。

為檢驗本文中 LR-ZF檢測算法的誤比特率性能，給出了4QAM和16QAM調制方式下的雙向中繼協同通信系統(tǒng)下傳統(tǒng)線性ZF、線性MMSE檢測算法性能。并且為方便比較，3種檢測算法均以AF方式轉發(fā)，并采用了LR-THP預編碼算法。仿真結果如圖6所示，LR-ZF檢測算法的誤比特率性能在圖中3種檢測算法中性能最優(yōu)。在Eb/N0為15 dB時，4QAM和16QAM調制方式下，相比于ZF檢測算法和 MMSE檢測算法，LR-ZF檢測算法的誤碼率降低了兩個數量級。并且在雙向中繼系統(tǒng)中本文的LR-ZF檢測算法仿真時間低于MMSE檢測算法，與 ZF檢測算法的仿真時間相當，這是由于在THP預編碼算法中，已經完成了對矩陣的預處理，降低了LR-ZF檢測算法的復雜度。

6 結論

本文針對多天線的雙向中繼協同通信系統(tǒng)，提出了一種用戶聯合預編碼與檢測算法。算法利用格規(guī)約理論改善信道增益矩陣的正交性，在兩用戶節(jié)點上利用 LR-THP算法對發(fā)送信號進行預編碼處理，中繼節(jié)點僅需要對接收到的信號進行求模運算和放大轉發(fā)，兩用戶節(jié)點接收到中繼轉發(fā)的信號后，利用LR-ZF算法對接收信號進行檢測。相比于傳統(tǒng)的預編碼和檢測算法，能夠大幅提高誤比特率性能。并且計算復雜度僅增加了對信道增益矩陣一次復數域格規(guī)約計算的過程，復雜度增加較小，具有一定的工程實用價值。

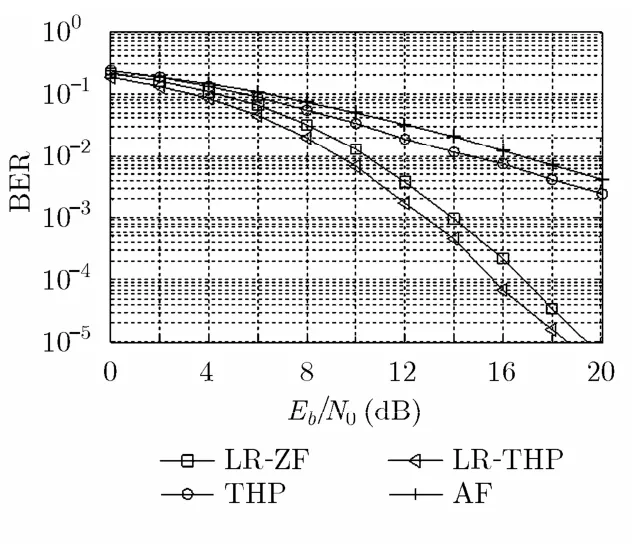
圖4 4QAM下預編碼的誤比特率性能比較

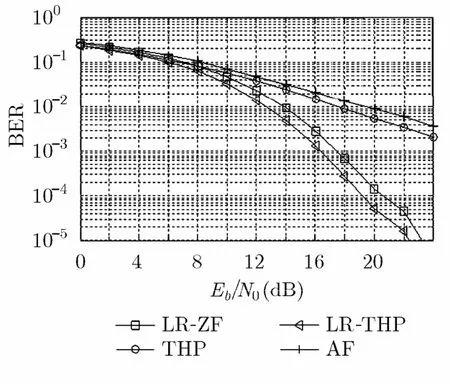
圖5 16QAM下預編碼的誤比特率性能比較

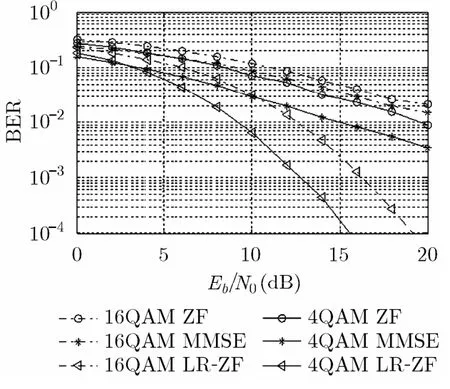
圖6 檢測算法的誤比特率性能比較

[1] Jianhua M, Meixia T, and Yuan L. Secure beamforming for MIMO two-way communications with an untrusted relay[J].IEEE Transactions on Signal Processing, 2014, 62（9）:2185-2199.

[2] 吉曉東, 鄭寶玉, 崔景伍. 不對稱雙向中繼信道中的再生雙向中繼選擇及功率分配[J]. 電子與信息學報, 2013, 35（7）:1707-1712.Ji Xiao-dong, Zheng Bao-yu, and Cui Jing-wu. Opportunistic relaying and power allocation for bidirectional regenerative relaying in asymmetric two-way relay channels[J]. Journal of Electronics & Information Technology, 2013, 35（7）:1707-1712.

[3] 芮國勝, 王林, 張洋, 等. 分布式雙向中繼選擇算法及用戶功率分配[J]. 通信學報, 2014, 35（5）: 1-7.Rui G S, Wang L, Zhang Y, et al.. Distributed two-way relay selection scheme and users power allocation[J]. Journal on Communications, 2014, 35（5）: 1-7.

[4] Rankov B and Wittneben A. Spectral efficient protocols for halfduplex fading relay channels[J]. IEEE Journal on Selected Areas in Communications, 2007, 25（2）: 379-389.

[5] Wooseok N, Chung Sae-young, and Lee Y H. Capacity bounds for two-way relay channels[C]. IEEE International Zurich Seminar on Digital Object Identifier. Zurich,Switzerland, 2008: 144-147.

[6] 趙睿, 傅友華, 李春國, 等. 多天線雙向中繼系統(tǒng)中的中繼處理與資源分配策略[J]. 電子與信息學報, 2010, 32（4）: 763-769.Zhao Rui, Fu You-hua, Li Chun-guo, et al.. Relay processing and resource allocation strategies for multi-antenna two-way relay system[J]. Journal of Electronics & Information Technology, 2010, 32（4）: 763-769.

[7] Sanguinetti L, D'Amico A A, and Rong Y. A tutorial on the optimization of amplify-and-forward MIMO relay systems[J].IEEE Journal on Selected Areas in Communications, 2012,30（8）: 1331-1346.

[8] Song C, Lee K-J, and Lee I. MMSE-based MIMO cooperative relaying systems: closed-form designs and outage behavior[J]. IEEE Journal on Selected Areas in Communications, 2012, 30（8）: 1390-1401.

[9] Wang J, Wang Y, Gui X, et al.. Robust relay precoding design for two way relay systems with delayed and limited feedback[J]. IEEE Communications Letters, 2013, 17（3）:689-692.

[10] Wang R and Tao M. Joint source and relay precoding designs for MIMO two-way relaying based on MSE criterion[J]. IEEE Transactions on Signal Processing, 2012, 6（3）: 1352-1365.

[11] Kossel M, Toifl T, and Francese P A. A 10 Gb/s 8-Tap 6b 2-PAM/4-PAM Tomlinson-Harashima precoding transmitter for future memory-link applications in 22-nm SOI CMOS[J].IEEE Journal of Solid-State Circuits, 2013, 48（12）:3268-3284.

[12] Wübben D, Seethaler D, and Jaldén J. Lattice reduction[J].IEEE Signal Processing Magazine, 2011, 50（5）: 70-91.

[13] Agrell E, Eriksson T, Vardy A, et al.. Closest point search in lattices[J]. IEEE Transactions on Information Theory, 2002,48（8）: 2201-2214.

[14] Senning C, Bruderer L, and Hunziker J. A lattice reductionaided MIMO channel equalizer in 90 nm CMOS achieving 720 Mb/s[J]. IEEE Transactions on Circuits and Systems I:Regular Papers, 2014, 61（6）: 1860-1871.

[15] Hung Ganying, Ling Cong, and Ho Mowwai. Complex lattice reduction algorithm for low-complexity full-diversity MIMO detection[J]. IEEE Transactions on Signal Processing, 2009,57（7）: 2701-2710.

[16] Yang Shao-hua and Qin Da-hua. Improved maximum likelihood sync mark detection for magnetic recording channels[J]. IEEE Transactions on Magnetics, 2013, 49（7）:3691-3694.

[17] Liu F, Jiang L, and He C. Advanced joint transceiver design for block diagonal geometric mean decomposition based multiuser MIMO systems[J]. IEEE Transactions on Vehicular Technology, 2010, 59（2）: 692-703.