非線性分?jǐn)?shù)階脈沖微分方程邊值問(wèn)題解的存在性
董 雪
(山東科技大學(xué) 數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院,山東 青島 266510)
?
非線性分?jǐn)?shù)階脈沖微分方程邊值問(wèn)題解的存在性
董雪
(山東科技大學(xué) 數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院,山東 青島 266510)
摘要:關(guān)于脈沖的非線性分?jǐn)?shù)階微分方程初邊值問(wèn)題已有研究,但細(xì)節(jié)過(guò)程仍存在問(wèn)題.證明了一類非線性分?jǐn)?shù)階脈沖微分方程在混合邊界條件下解的存在性,結(jié)果的證明主要依據(jù)了schaefer不動(dòng)點(diǎn)定理.最后舉例說(shuō)明了所得結(jié)果的正確性.
關(guān)鍵詞:非線性分?jǐn)?shù)階微分方程;脈沖;混和邊值問(wèn)題;不動(dòng)點(diǎn)定理
目前,非線性分?jǐn)?shù)階微分方程邊值問(wèn)題已經(jīng)引起許多研究者的注意.分?jǐn)?shù)階微分方程作為一種系統(tǒng)和流程的數(shù)學(xué)模型出現(xiàn)在許多工程和科學(xué)學(xué)科領(lǐng)域,如物理、化學(xué)、控制理論、生物學(xué)、經(jīng)濟(jì)學(xué)、血液流動(dòng)現(xiàn)象、信號(hào)和圖像處理、空氣動(dòng)力學(xué)、實(shí)驗(yàn)數(shù)據(jù)擬合等等.關(guān)于詳細(xì)資料可參考文獻(xiàn)[1-7].脈沖微分方程給出了觀察進(jìn)化過(guò)程的一個(gè)自然的描述,作為一個(gè)重要的數(shù)學(xué)工具可更好地理解應(yīng)用科學(xué)中許多現(xiàn)實(shí)問(wèn)題.目前,整數(shù)階脈沖微分方程邊值問(wèn)題已經(jīng)被廣泛的研究,如文獻(xiàn)[8-11].但是,很少有文章考慮關(guān)于分?jǐn)?shù)階的非線性脈沖微分方程邊值問(wèn)題.
本文中我們研究下述非線性分?jǐn)?shù)階脈沖微分方程混合邊值問(wèn)題解的存在性.
(1)
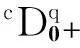
1 預(yù)備知識(shí)
為了證明主要結(jié)果,本章節(jié)介紹一些文中所要用到的預(yù)備知識(shí).


定義1階為q的函數(shù)f:[0,]→R的分?jǐn)?shù)階積分公式定義為
(2)
定義2分?jǐn)?shù)階為q的函數(shù)f:[0,]→R的Caputo導(dǎo)數(shù)公式定義為
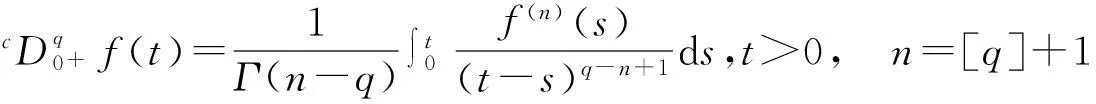
(3)
式中[q]記為實(shí)數(shù)q的整數(shù)部分.

引理2令q∈(1,2)且h:J→R是連續(xù)的.函數(shù)u給定如下:
(4)
為下面脈沖問(wèn)題的唯一解.
(5)
2 主要結(jié)果
本章節(jié)我們證明問(wèn)題(1)解的存在性.
定理1假設(shè)
(A1) 函數(shù)f:J×R→R為連續(xù)函數(shù),且存在常數(shù)N1>0使得

(A2) 函數(shù)Ik,Jk:R→R為連續(xù)函數(shù),且存在常數(shù)N2,N3>0使得
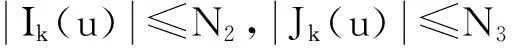
則問(wèn)題(1)至少有一個(gè)解.
證明第一步:定義算子T:PC(J,R)→PC(J,R)如下:
t∈(tk,tk+1],j=1,2,…,p,k=0,1,2,…,p-1.


本評(píng)分模型納入預(yù)后因素時(shí)未加入雙磷酸鹽的使用,原因是本研究中幾乎所有骨轉(zhuǎn)移患者皆使用過(guò)雙膦酸鹽,且雙膦酸鹽的使用對(duì)骨轉(zhuǎn)移患者預(yù)后的影響已基本明確,已成為常規(guī)治療方案[14]。本評(píng)分模型的缺點(diǎn)在于只基于一家醫(yī)療機(jī)構(gòu)的數(shù)據(jù),存在選擇偏倚,且納入因素有九個(gè)之多,準(zhǔn)確性和實(shí)用性尚需更大樣本數(shù)據(jù)的檢驗(yàn),需要本機(jī)構(gòu)和其他醫(yī)療機(jī)構(gòu)在日后臨床工作中進(jìn)行實(shí)踐,不斷改進(jìn),更加準(zhǔn)確的指導(dǎo)臨床。



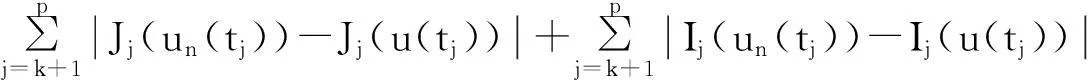
因?yàn)閒,Ik,Jk為連續(xù)函數(shù),所以當(dāng)n→時(shí)有‖Tun-Tu‖→0.所以,T:PC(J,R)→PC(J,R)是連續(xù)的.

由(A1)和(A2)可得,對(duì)于任意的t∈J有


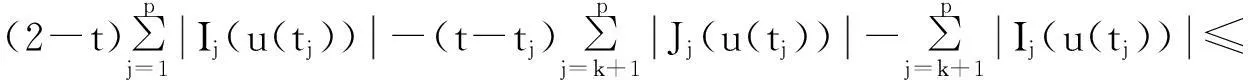
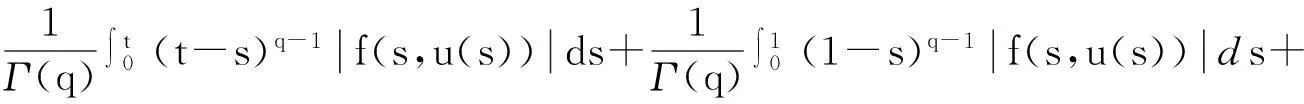




第三步:令Ωρ為如第二步中所定義的PC(J,R)上的有界集合,且令u∈Ωρ,則對(duì)于任意的t∈Jk,0≤k≤p有



因此,令t″,t′∈Jk,t′ 所以,在Jk(k=0,1,2,…,p)上T(Ωρ)是等度連續(xù)的.因此,綜上可得T:PC(J,R)→PC(J,R)是全連續(xù)的. 根據(jù)條件(A1)和(A2)可得,對(duì)于任意的t∈J有 因此,對(duì)于任意的t∈J有 所以集合V是有界的.所以由引理1可得算子T有一個(gè)不動(dòng)點(diǎn)即為問(wèn)題(1)的一個(gè)解. (6) 參考文獻(xiàn): [1] Zhou W X, Chu Y D, Dumitru B. Uniqueness and existence of positive solutions for a multi-point boundary value problem of singular fractional differential equations[J]. Advances in Difference Equations, 2013(1): 114. [2] Wang G T,Ravi P, Alberto C,etal. Existence results and the monotone iterative technique for systems of nonlinear fractional differential equations[J]. Applied Mathematics Letters, 2012, 25(6): 1019-1024. [3] Tadeusz J. Initial value problems for neutral fractional differential equations involving a Riemann-Liouville derivative[J]. Applied Mathematics and Computation, 2013, 219(14): 7772-7776. [4] Wu J W, Zhang X G, Liu L S,etal. Positive solutions of higher-order nonlinear fractional differential equations with changing-sign measure[J]. Advances in Difference Equations, 2012(1):1-14. [5] Seak W V. Positive solutions of singular fractional differential equations with integral boundary conditions[J].Mathematical and Computer Modelling, 2013, 57(5-6):1053-1059. [6] Liu Z H, Sun J H, Ivan S. Monotone Iterative Technique for Riemann- Liouville fractional integro-differential equations with advanced arguments[J]. Results in Mathmatics, 2013, 63(3-4): 1277-1287. [7] LiuR J, Kou C H, Jin R. Multiple positive solutions of boundary value problems for fractional order integro-differential equations in a Banach space[J]. Boundary Value Problems, 2013(1):1-18. [8] Lee E K, Lee Y H. Multiple positive solutions of singular two point boundary value problems for second order impulsive differential equation[J]. Applied Mathematics and Computation, 2004, 158(3):745-759. [9] Lin X N, Jiang D Q. Multiple positive solutions of Dirichlet boundary value problems for second order impulsive differential equations[J]. Journal of Mathematical Analysis and Applications, 2006, 321(2): 501-514. [10] Nieto J J, Lope R R. Boundary value problems for a class of impulsive functional equations[J]. Computers and Mathematics with Applications, 2008, 55(12): 2715-2731. [11] Shen J H, Wang W B. Impulsive boundary value problems with nonlinear boundary conditions[J]. Nonlinear Analysis, 2008, 69(11):4055-4062. [12] Sun J X. Nonlinear functional analysis and its application[M]. Beijing: Science Press, 2008. (編輯:姚佳良) Existenceofsolutionsforimpulsivenonlinear fractionaldifferentialequationsboundaryvalueproblems DONGXue (CollegeofMathematicsandSystemScience,ShandongUniversityofScienceandTechnology,Qingdao266510,China) Abstract:The initial value problems and boundary value problems of impulsive nonlinear fractional differential equations had been studied,but there were still some details which were not appropriate. We proved the existence of solutions for an impulsive mixed boundary value problem of nonlinear differential equations of fractional order. Our result is based on schaefer′s fixed point theorem. Finally, an example was presented to illustrate the result. Key words:nonlinear fractional differential equations; impulse; mixed boundary value problem; fixed-point theorem 中圖分類號(hào):O175.8 文獻(xiàn)標(biāo)志碼:A 文章編號(hào):1672-6197(2015)04-0070-05 作者簡(jiǎn)介:董雪,女,dx929wdl66@163.com 收稿日期:2014-11-14



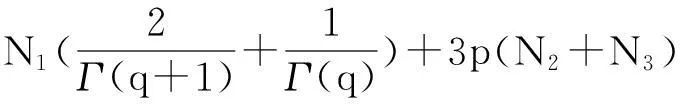

3 舉例



