基于MATLAB仿真的數字PID控制器設計方法

張 策

(哈爾濱工業(yè)大學信息與電氣工程學院，山東威海264200)

在機電控制系統(tǒng)的設計中，PID控制是生產過程中的一種閉環(huán)控制方法，而PID控制器則是在工業(yè)控制之中常見的一種反饋回路補件，又分為比例單元P、積分單元I和微分單元D［1-3］。PID控制原理簡單、使用方便、適用性強及魯棒性強，而且易于整定。同時，其控制品質對被控對象的變化并不敏感，因此得到廣泛的應用［4-5］。常規(guī)PID控制參數的最佳調整還未實現自動化，依靠人工試湊的整定方法不僅需要豐富的經驗和技巧，而且十分費時［6-7］。同時，在實際控制系統(tǒng)控制過程中，由于噪聲、負載擾動和其他一些環(huán)境條件變化的影響，受控過程參數、模型結構均將發(fā)生變化。在這種情況下，采用常規(guī)PID控制器難以獲得滿意的控制效果。因此，本文基于MATLAB仿真得到一種數字PID控制器的設計方法，使得PID控制參數易于調整且具有普適性，為實際控制系統(tǒng)的設計與調試提供了理論參考依據。

1 基于MATLAB仿真的數字PID控制器設計方法

1．1 PID控制器設計原理

設計需要具體參數，本文取單位反饋系統(tǒng)的開環(huán)傳遞函數如式(1)所示:

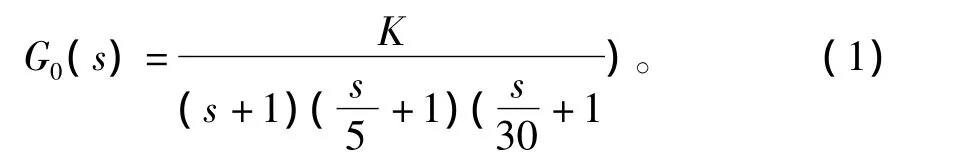
系統(tǒng)的穩(wěn)態(tài)誤差不大于0．1，超調量不大于20%，調節(jié)時間不大于0．5 s。算法方面采用位置式算法，這是一種PID算法的表現形式。

離散的PID表達式如式(2)所示:

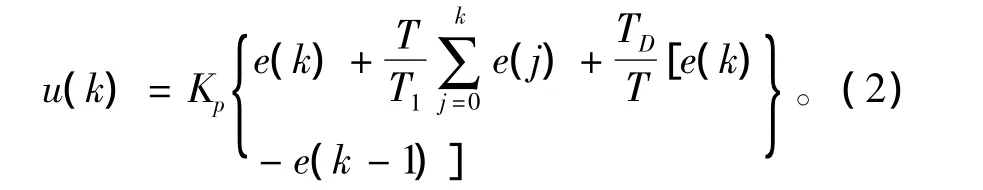
使用模擬控制器離散化的方法，將理想模擬PID控制器D(s)轉化為響應的理想數字PID控制器D(z)。采用后向差分法得到數字控制器的脈沖傳遞函數，如式(3)所示:

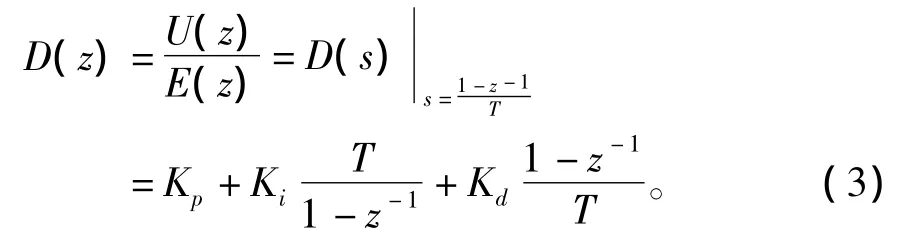
1．2 基于MATLAB仿真的數字PID參數選擇

在此采用擴充臨界比例帶法來整定PID參數，擴充臨界比例帶法是以模擬PID調節(jié)器中使用的臨界比例帶法為基礎的一種數字PID參數的整定方法［8-9］，主要包含兩個步驟:①選擇合適的采樣周期T;②在純比例的作用下，給定輸入階躍變化時，逐漸加大比例作用Kp(即減小比例帶)，直至系統(tǒng)出現等幅震蕩，記錄比例增益Kc，及振蕩周期Tc。Kc成為臨界振蕩比例增益(對應的臨界比例帶)，Tc成為臨界振蕩周期。

在MATLAB中對以上步驟進行編程，得到初步參數模擬結果，如圖1所示。

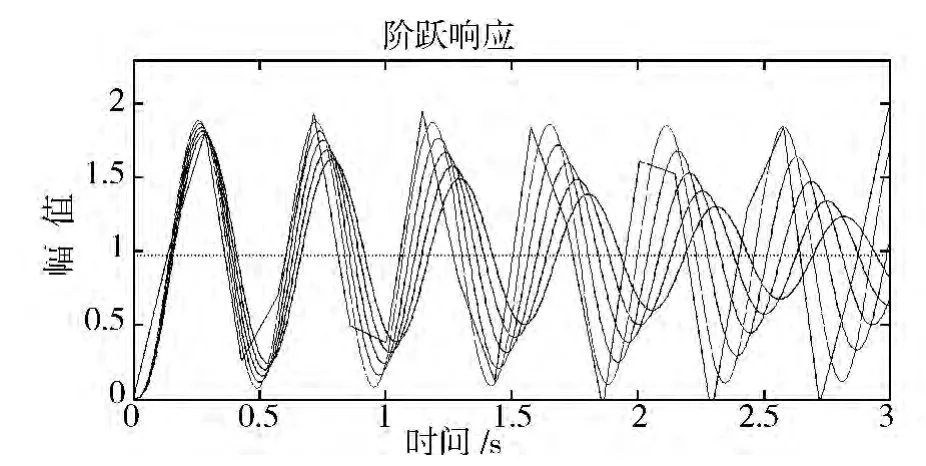
圖1 初步階躍響應曲線Fig．1 Preliminary step response curves

在初步結果的基礎上改變范圍和步長為p=［40∶1∶45］，得到如圖2所示調整后的結果。

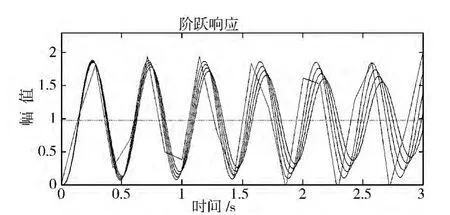
圖2 調整后階躍響應曲線Fig．2 Adjusted step response curves

通過圖形變化趨勢，進一步精確取得Kc的值為43(中間值)，Tc約為0．5。

擴充臨界比例帶法選擇數字PID參數的計算公式見表1。

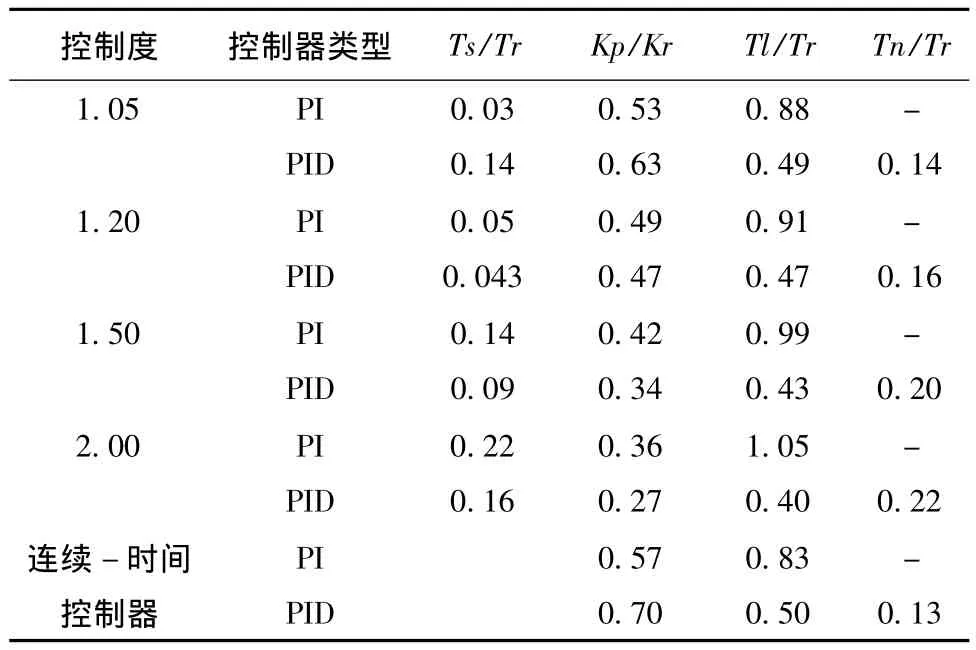
表1 擴充臨界比例度法數字PID控制器的參數計算公式Tab．1 Formula of the digital PID controller's parameters with extended critical ratio method

1．3 控制度選擇

控制度為數字調節(jié)器和模擬調節(jié)所對應的國度過程的誤差平方積分之比［10-11］，即:

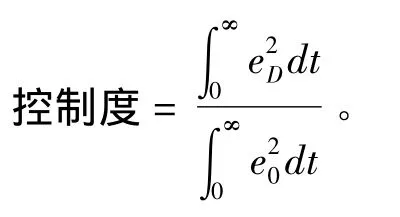
式中:e0為數字調節(jié)器的控制誤差;e為模擬調節(jié)器的控制誤差。

當控制度為1．05時，數字調節(jié)器與模擬調節(jié)器的控制效果相當;當控制度為2時，數字調節(jié)器比模擬調節(jié)器的控制效果差一倍。

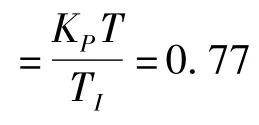
1．4 Simulink 模型建立

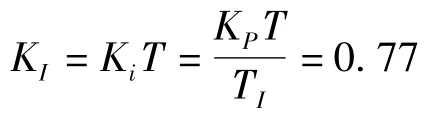
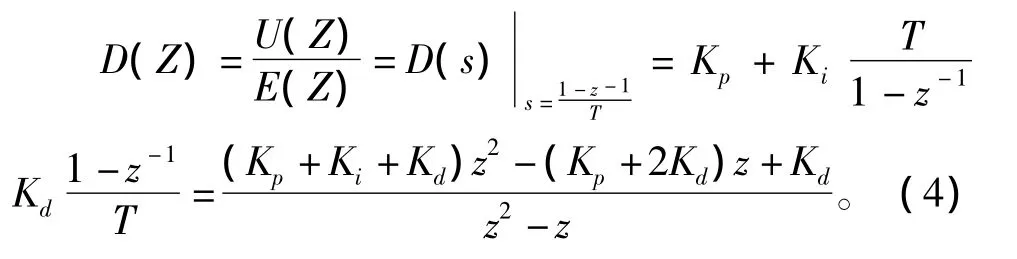
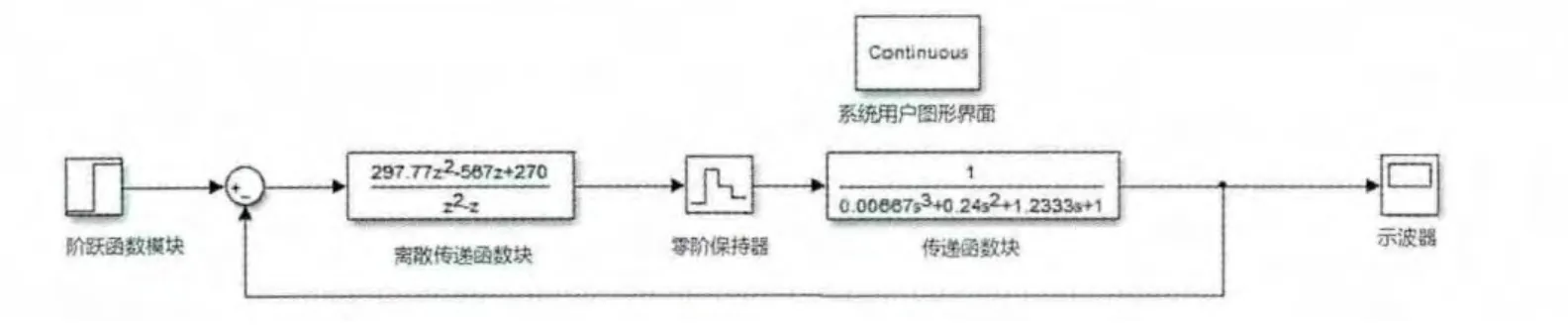
圖3 Simulink模型Fig．3 Simulink model

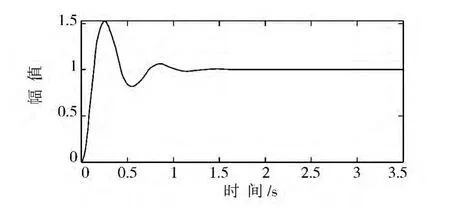
圖4 Scope中階躍響應曲線Fig．4 Step response curve in Scope

由圖4可知，模型的超調量較大，調節(jié)時間較長，需更換整定方法。因此嘗試用試湊法得到一組數據:T=0．015，Kp=15，Ki=0．23，KD=250。將其帶入MATLAB-Simulink模型，模型發(fā)生變化，結果如圖5所示，其在Scope中的階躍響應圖形如圖6所示。

由圖6可知，用試湊法得到的數據滿足設計要求，即:系統(tǒng)的穩(wěn)態(tài)誤差不大于0．1，超調量不大于20%，調節(jié)時間不大于0．5 s。

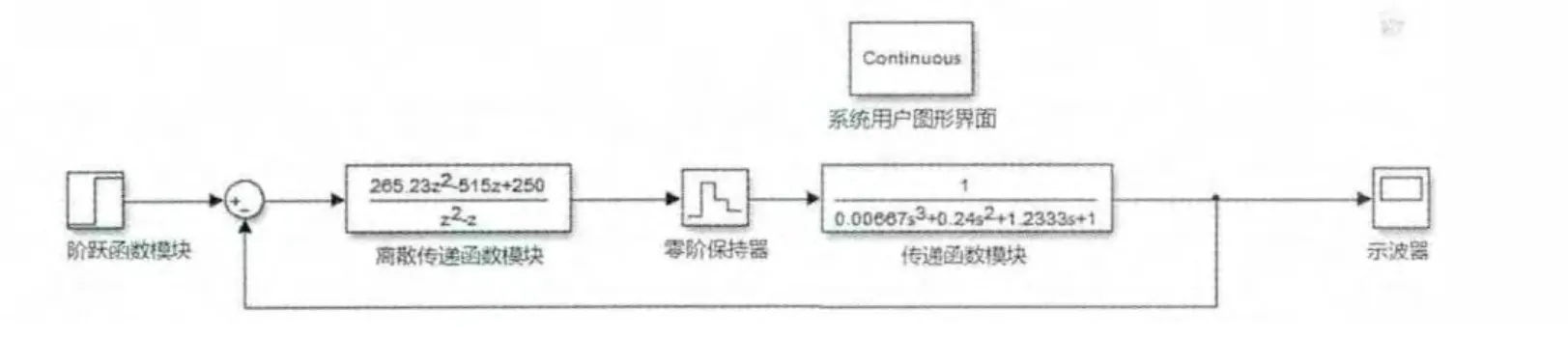
圖5 調整后Simulink模型Fig．5 Adjusted Simulink model

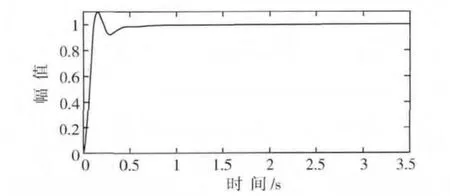
圖6 調整后Scope中階躍響應曲線Fig．6 Adjusted step response curves in Scope

2 MCS-51單片機實現控制器的設計

軟件設計完成之后需要硬件實現，這里采用MCS-51單片機來實現算，其控制系統(tǒng)結構框圖如圖7所示。

圖7 控制系統(tǒng)結構框圖Fig．7 The structure diagram of a controller systerm

2．1 器件選擇

主控制器選用熟悉的AT89c51單片機。由于沒有對精度的要求，選用常見的8位AD/DA芯片ADC0809和DAC0832［12］。由于系統(tǒng)要求采樣周期0．015 ms，而上述 AD、DA芯片轉化時間很短(ADC0809 約100 μs，DAC0832 約 1 μs)，因此上述芯片滿足要求。

2．2 電路設計

單片機與AD、DA采用總線方式連接，鎖存器74LS373進行地址鎖存。采用統(tǒng)一編址方式訪問［13］。

控制器程序下載到單片機內部，經單片機處理，輸出為數字信號，通過DAC0832將數字量轉換為模擬量，作為被控對象的輸入，被控對象的輸出也為模擬量，經過ADC0809處理，模擬量轉換為數字量，送入單片機內，完成閉環(huán)控制。

其中，ADC0809與單片機連接如圖8所示，DAC0832與單片機連接如圖9所示。

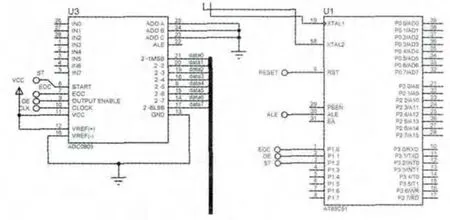
圖8 ADC0809與單片機連接示意圖Fig．8 Connection schematic diagram of ADC0809 and MCU

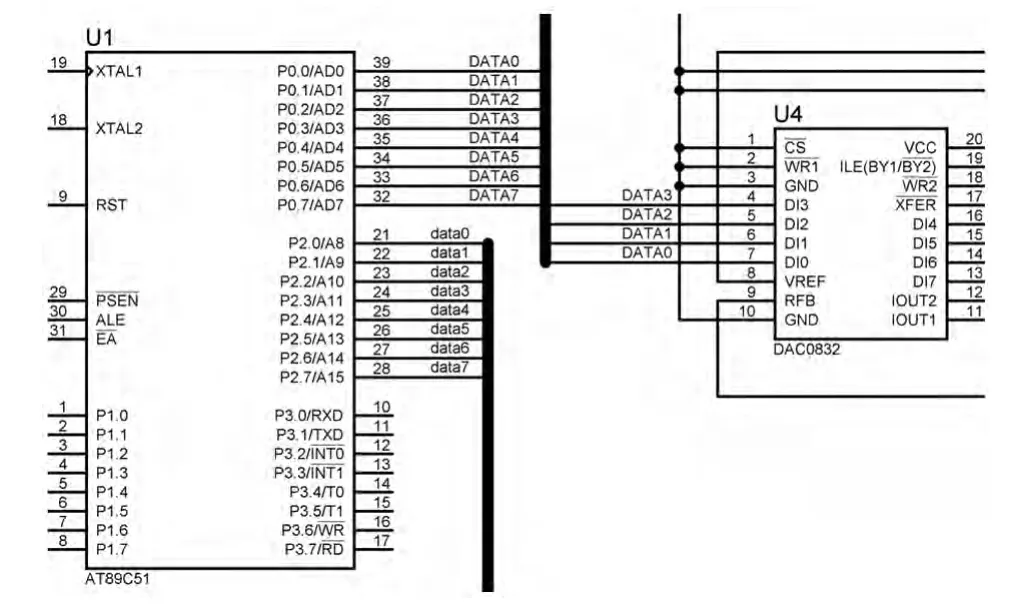
圖9 DAC0832與單片機連接示意圖Fig．9 Connection schematic diagram of DAC0832 and MCU

3 結束語

本文基于MATLAB仿真得到了一種數字PID控制器的設計方法，并對模擬結果進行驗證。結果表明:本設計方法簡單有效，切實可行，參數易于調整且具有普適性。這種設計方法可以應用于對控制精度要求較高的工業(yè)生產過程中，為實際控制系統(tǒng)的設計與調試提供了理論參考依據。

［1］楊 智，朱海鋒，黃以華．PID控制器設計與參數整定方法綜述［J］．化工自動化及儀表，2006，32(5):1-7．

［2］于曉敏，于曉坤，耿 蕊．PID控制器參數優(yōu)化算法的仿真研究［J］．計算機仿真，2011，28(7):212-215．

［3］鄭劍翔．運用Matlab實現 PID控制器的設計［J］．福州大學學報:自然科學版，2011，39(6):898-903．

［4］晏亭太．智能自適應PID/PD控制器設計及仿真研究［D］．哈爾濱:哈爾濱工業(yè)大學，2014，16-29．

［5］張燕紅．PID控制器參數自整定方法綜述［J］．常州工學院學報，2008，21(4):49-53．

［6］李 瑞，劉明生，李 燕．基于MATLAB的模糊PID控制器的設計與研究［J］．科技創(chuàng)新與應用，2013(29):33-34．

［7］王麗飛．PID控制器參數整定方法研究［D］．青島:中國石油大學，2008，15-24．

［8］楊 璐，雷菊陽．基于MATLAB的參數自整定模糊PID控制器的兩種設計方法［J］．計算機測量與控制，2015，23(4)，1212-1214．

［9］田 海，李 軍．基于Matlab的模糊自整定PID控制器仿真研究［J］．工業(yè)控制計算機，2011，24(6):24-25．

［10］羅海波．PID控制器設計與仿真研究［J］．計算機仿真，2012，29(2):345-348．

［11］鄭美茹．模糊PID控制器的仿真研究［J］．裝備制造技術，2011(4):74-76．

［12］王 輝，王 琀．其于遺傳算法和近鄰分類器識別率的特征選擇方法［J］．林業(yè)機械與木工設備，2015，43(9):26-27．

［13］賀昌勇，張厚江，祖漢松，等．基于虛擬儀器運動控制技術的現狀與發(fā)展趨勢［J］．林業(yè)機械與木工設備，2014，42(2):9-12．