基于阿爾茨海默病的基因表達數據改進的一維聚類方法

黃 靜， 付如意， 彭志紅， 胡本瓊， 龐朝陽

(1.四川師范大學數學與軟件科學學院，四川成都610066;2.解放軍四五二醫院肛腸科，四川成都610021;3.成都理工大學管理科學學院，四川成都610059;4.四川師范大學計算機科學學院，四川成都610066;5.四川師范大學可視化計算與虛擬現實四川省重點實驗室，四川成都610066)

阿爾茨海默癥，即老年癡呆癥，是一類神經退行性疾病，已成為繼心血管疾病、惡性腫瘤、腦卒中之后老年人的第4大“健康殺手”［1］.目前，世界上并沒有治療老年癡呆癥的有效辦法.隨著基因芯片技術［2-5］的迅速發展，2003年與阿爾茨海默病相關的基因表達數據能夠在公共生物信息數據庫中獲取［6］.2009 年 W.Kong 等［7］將獨立主成分分析(ICA)方法應用于阿爾茨海默病的候選基因的識別中.2010年龐朝陽等將聚類分析方法應用到阿爾茨海默病的致病基因的識別中［8］.為了高效快捷地挖掘基因表達數據，簡捷的一維聚類方法在一些情形下能夠被應用.但是它需要事先主觀的確定出分類數目K.因此，本文基于擬合的思想在一維聚類分析方法的基礎上提出了將曲率最大點處的距離作為分類判據，從而實現無監督的一維聚類分析.

1 預備知識

1.1 主成分分析方法 主成分分析(PCA)是一種對高維數據進行分析、簡化的技術.這種方法本質上是找出高維數據中最“主要”的元素和結構，去除噪音和冗余，將原有數據降維，把多指標轉化為少數幾個綜合指標，揭示隱藏在復雜數據背后的簡單結構［1］.

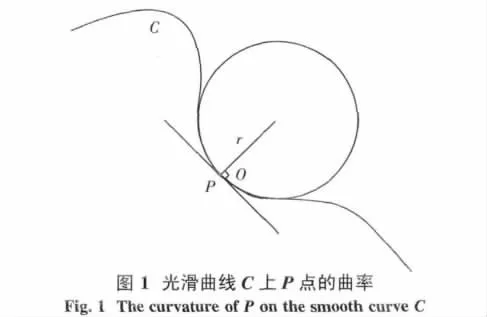
1.2 光滑曲線的曲率 曲率［1］是平面曲線彎曲程度的直觀描述.現給出光滑曲線的曲率的數學語言描述.假設光滑曲線C為y=f(x)，則該曲線上任一點P的曲率κ可表示為一個指向該圓圓心的大小等于密切圓半徑的倒數的向量，如圖1所示，即

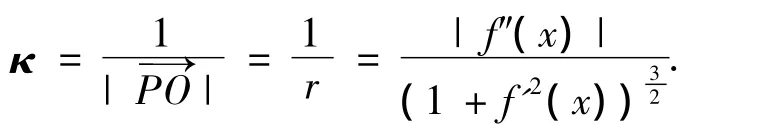
1.3 最小二乘估計 最小二乘法(又稱最小平方法)是一種數學優化技術.目標是最小化誤差的平方和尋找數據的最佳逼近函數.利用最小二乘法可以簡便地求得未知的數據，并使得這些求得的數據與實際數據之間誤差的平方和為最小.通常，最小二乘法用于曲線擬合［1，9-10］.

2 數據的來源與特征

本文從美國國家生物技術信息中心(NCBI)網站獲取到了關于阿爾茨海默病患者的基因綜合表達數據［6］.該數據是從正常、輕度、中度以及重度4種程度的患者的海馬體組織中利用基因芯片技術提取出的人體的22 283個基因的表達水平，其數據格式如表1，其中數值已經過對數化平滑處理.

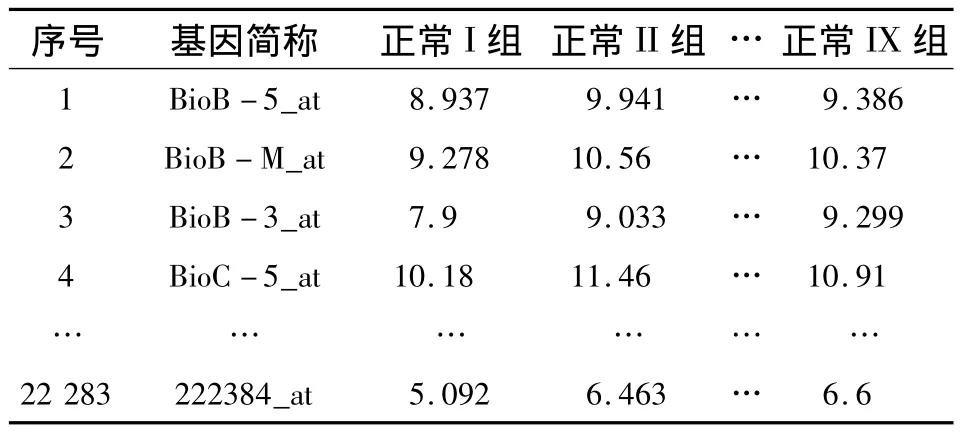
表1 基因表達水平數據表(以正常組為例)Table 1 Organization of gene expression data(as an example of the control group)

由上述數據可以得出兩點信息:一是表1中的每列數據對應于一個給定的實驗條件(或人體組織);二是由于每一行對應于同一個基因的表達水平，則列數據之間必然存在相關性.于是可以考察阿爾茨海默病同一程度的任意2組患者間的基因表達水平分布情況.

接下來以表1的數據為例進行具體說明.

第一步，標準化處理表1的各列數據Xi=［xi1，xi2，…，xi22283］(i=1，2，…，9).則

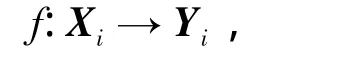
其中，

第二步，由此得到任意兩列形成的基因表達水平的二維分布數據列，如圖2 所示.令［Yi，Yj］(i，j=1，2，…，9)且 i≠j.

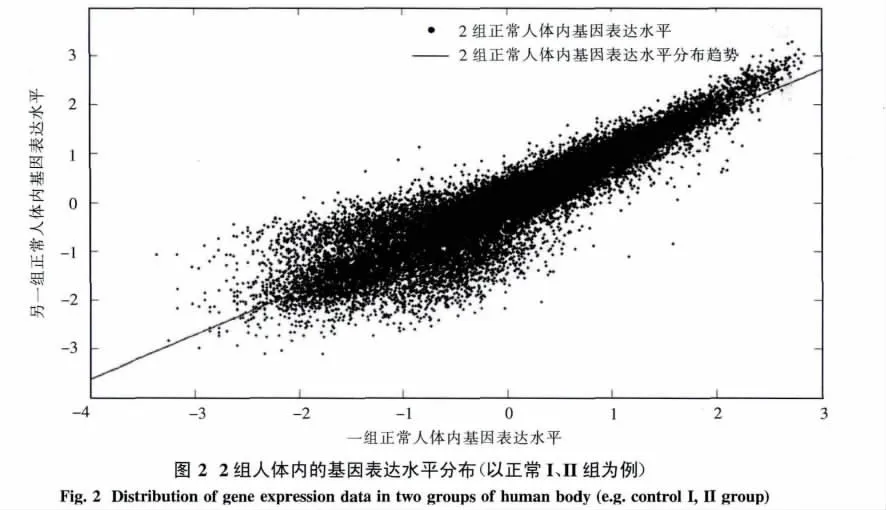
通過觀察形如圖2所示的4種程度的基因表達水平的二維分布圖，可以發現所有的點集中在一條直線的周圍.這表明，各基因在不同條件下呈線性相關性.從而通過主成分分析方法將數據進行降維處理，得到一維投影點數據，記為集合

進一步地，得到了在一維投影子空間中相鄰一維投影點間的距離，記為集合

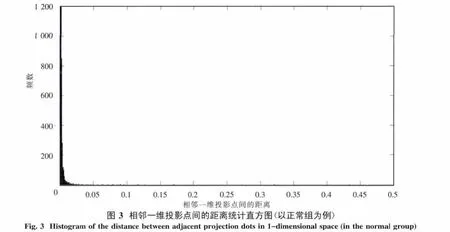
Q={di=pi+1-pi|i=1，2，…，22 283}，并做出統計直方圖，其中橫軸表示相鄰投影點間的距離，縱軸表示距離所對應的頻數，如圖3所示.

由圖3得知相鄰一維投影點間的距離主要都分布在0.05以內，呈現出聚類特征.基于此，考慮對一維投影點進行聚類處理.

3 改進的一維聚類方法

目前通用的一維聚類方法需要事先確定出類別數目K的大致范圍.在數據分析的實際處理過程中，這往往存在著很大的主觀因素，甚至分析者根本無法合理地確定分類數目.通過處理阿爾茨海默病的基因數據，本文提出一種改進的無監督一維聚類方法:將相鄰一維投影點間的距離統計數目的趨勢線的曲率最大點作為分類判據δ進行無監督的一維數據聚類處理.接下來本文將具體描述該方法的分類判據的確定過程.

首先給出分類判據δ的具體意義.對于任意給定的2個類 C1和 C2，如果 p1∈C1且 p2∈C2，則‖p1-p2‖≥δ.如果 p1，p2∈Ci(i=1，2)，則‖p1-p2‖ ＜δ.

從而進一步定義下面2個概念:

定義1 最小類間距離，即2個類簇間的距離

定義2 最大類內距離，即同一個類內，一個點和它的相鄰點的距離

Dmax=sup{‖pi-pj‖ |pi，j∈ Ck，Ck? P}.因此，顯然有 Dmax≤δ≤Gmin，即這樣的“δ”作為聚類投影點的分類判據.其次，通過最小二乘估計方法得到的光滑曲線必然存在一點A，使得在A點左側的區域屬于類內距離集合，并且在A點右側的區域屬于類間距離集合.該曲線的曲率最大點處的距離介于類內距離與類間距離之間，即滿足分類判據的條件.因此曲率最大點 處的距離將作為分類判據“δ”的取值是合理的.

4 實驗與結果

結合阿爾茨海默病基因數據，將具體給出分類判據δ的計算過程.對集合Q進行統計計數得到如圖3所示的直方圖.很清楚地看到相鄰投影點間的距離的頻數隨著距離的增大而逐漸遞減并呈現出指數曲線的趨勢.于是通過最小二乘估計方法擬合得到指數曲線F(x)=1.52e1121x(其擬合優度R=0.996)，如圖4所示.

根據光滑曲線的曲率表示形式，曲線的曲率

由極值的必要條件［11］有 G'(δ)=0，解得 δ=0.006 9.此外，進一步作出指數曲線的曲率的圖像以驗證結果是正確的，如圖5所示.

5 結論

目前，聚類分析統計方法［12-16］已經被應用到阿爾茨海默病的致病基因的識別過程中.通過分析阿爾茨海默病的基因表達數據，本文提出了將曲率最大點作為分類判據的一種無監督的一維聚類方法.并且應用阿爾茨海默病的基因表達數據計算出了其分類判據δ.

［1］維基媒體基金會.維基百科［EB/OL］.http://zh.wikipedia.org/，2014.

［2］Yang J H.基因表達水平估計策略和方法［EB/OL］.http://www.plob.org/2012/10/01/3887.html，2014.

［3］Zhao Y B.RPKM 簡介［EB/OL］.http://www.plob.org/2011/10/24/294.html，2014.

［4］李瑤.基因芯片技術:解碼生命［M］.北京:化學工業出版社，2004:77-156.

［5］朱明華.組織微陣列及其在腫瘤病理研究中的應用［J］.中華病理學雜志，2002，31(1):72-74.

［6］Blalock E M，Geddes J W，Chen K C，et al.Incipient Alzheimer's disease:Microarray correlation analyses reveal major tran-scriptional and tumor suppressor responses［J］.PNAS，2004，101:2173-2178.

［7］Kong W，Mou X Y，Yang B.Study DNA microarray gene expression data of Alzheimer's disease by independent component analysis［C］//Bioinformatics，Systems Biology and Intelligent Computing.Inter Joint Conf IEEE，2009:44-47.

［8］Pang C Y，Hu W，Hu B Q，et al.A special local clustering algorithm for identifying the genes associated with Alzheimer's disease［J］.IEEE Trans Nanobioscience，2010，9(1):44-50.

［9］馬昌鳳，林偉川.現代數值計算方法［M］.北京:科學出版社，2008:179-193.

［10］茆詩松，王靜龍，濮曉龍.高等數理統計［M］.2版.北京:高等教育出版社，2006:128-135.

［11］華東師范大學數學系.數學分析上冊［M］.3版.北京:高等教育出版社，2001:163-165.

［12］［美］Han J W，Kamber M，Pei J.數據挖掘:概念與技術［M］.3版.范明，孟小峰，譯.北京:機械工業出版社，2012:327-543.

［13］胡本瓊，張先迪，龐朝陽.利用圖論設計圖像壓縮中的向量量化聚類算法［J］.四川師范大學學報:自然科學版，2005，28(3):376-378.

［14］王開軍，李曉.基于有效性指標的聚類算法選擇［J］.四川師范大學學報:自然科學版，2011，34(6):915-918.

［15］莊劉，曾艷.基于模糊C-均值聚類的最優量化器設計［J］.四川師范大學學報:自然科學版，2010，33(4):559-562.

［16］宋麗紅.K-均值聚類的Matlab仿真設計［J］.實驗技術與管理，2010，27(10):101-103.