基于遺傳算法對車輛振動模型目標函數的優化及仿真研究

郭偉東

（南京交通職業技術學院，南京 211188）

基于遺傳算法對車輛振動模型目標函數的優化及仿真研究

郭偉東

（南京交通職業技術學院，南京 211188）

本文從遺傳算法的角度出發，對車輛振動模型的目標函數進行優化，并與以前研究理論成果進行對比分析。首先，分析了目標函數的遺傳算法程序，同時考慮車輛振動模型中的相關函數；其次，創建車輛振動模型，對相關目標函數進行優化，采取2-目標，優化車輛的前輪速度、后輪速度、座椅加速度、簧載質量、前輪的相對位移及后輪的相對位移；最后，采用matlab軟件，對目標優化處理結果進行仿真，并與以前的仿真結果進行對比分析。優化后仿真結果顯示，采取多目標遺傳算法對車輛振動模型進行優化后，車輛行駛過程中經過地面障礙物時，座椅振動相對較小，舒適性良好。

遺傳算法 車輛振動 優化 仿真

引言

隨著經濟全球化的發展，居民的生活水平顯著提高，汽車成為眾多家庭出門的重要交通工具，而發展汽車產業已成為各國發展經濟的重要舉措之一。面對多種汽車品牌的快速發展，汽車行駛過程中的舒適性成為衡量汽車性能的重要指標之一。駕駛員駕駛舒適性較好的汽車，經過障礙物時，車輛行駛平穩，不會造成乘客不適應，也很少使乘客出現難受、嘔吐等不良現象。因此，汽車的舒適性指標在未來汽車發展過程中會越來越受到重視，其將成為各國汽車企業研究的重點。如何才能降低或避免汽車在行駛過程中的振動，成為當前汽車行業研究的重點。

目前，已有許多研究人員從不同角度對車輛振動進行了研究。例如：劉波、Paul D.Walker等學者[1-3]對車輛—路面空間耦合振動模型及其動力響應展開研究；Semih Sezer、張有為、Eckardt Johanning等人[4-6]對車輛—軌道耦合系統高效隨機振動進行了分析和優化；曾銳、Le Thanh Danh、Tadeusz Majewski等人[7-9]對汽車動力傳動系扭振分析及其對車輛的振動影響進行了研究。但是，研究人員對車輛振動研究的內容還不夠全面，如優化目標函數時，只針對一個函數進行優化，難以保證汽車在行駛過程中的舒適性，導致汽車產品在同行業競爭中缺乏優勢。對此，本文采用遺傳算法的優化方法，對車輛振動模型的目標函數進行優化。同時，將研究理論成果與以前成果進行對比分析。采取2-目標優化方法，優化車輛的前輪速度、后輪速度、座椅加速度、簧載質量、前輪的相對位移及后輪的相對位移，并借助matlab軟件對2-目標優化處理結果進行仿真。優化仿真結果表明，采用遺傳算法對車輛振動模型進行優化處理后，車輛行駛過程中經過地面障礙物時，座椅振動相對較小，舒適性良好，從而為汽車整體設計研究提供了重要參考。

1 帕雷托優化

1.1 帕雷托前沿的定義

對一個目標函數優化處理問題，帕雷托前沿[10]PT*是一個目標函數向量的集合。通過使用帕雷托集合 P*中的決策變量向量可以得到該集合，它可以定義為公式（1）。

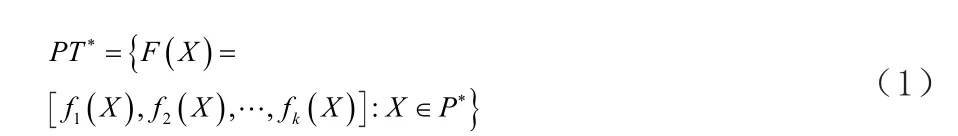
因此，可以說，帕雷托前沿PT*是從P*映射過來的目標函數向量的集合。

1.2 帕雷托優化

帕雷托優化通常是對多種條件或向量同時存在的情況下進行優化，它是對滿足已知條件下，搜索出目標函數給出的優化值。通常情況下，帕雷托在數學表達式中定義如下。

對一個目標向量X*=[x1*，x2*，…，xn*]T進行優化，定義如公式（2）。

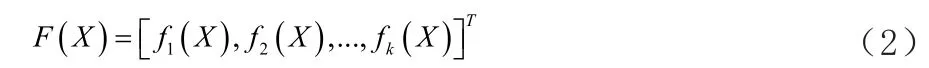
它要滿足式（3）和式（4）中的不等式約束條件。

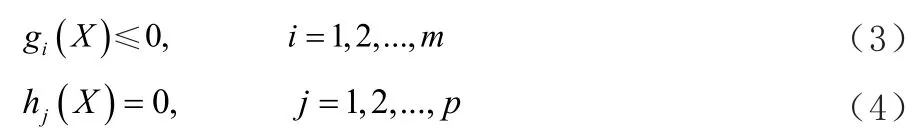
其中，X*代表設計變量向量，式（2）中，F(X)代表目標函數向量，所有向量都必須滿足極端值（最大化或者最小化）。但是，在許多情況下，目標函數一般都假設為最小化。因此，可以借用某種定義解決帕雷托前沿目標函數的最小化。

1.3 帕雷托最優點定義

當可行區域內的一個點X*∈Ω(Ω是Rn中同時滿足公式（3）和公式（4）的可行區域)對其它所有的點X∈Ω，且滿足F(X*)＜F(X)，則該點定義為帕雷托最優點。從另一個方面，它也可以被定義為：?X∈Ω―{X*} fi（X*）≤fi（X）∧?j∈{1，2，…，k}: fj（X*）≤fj（X）。也就是說，在沒有找到帕累托定義的其它方式對X*進行支配解的情況下，帕雷托最優解(通常是最小解)就是X*。

2 遺傳算法

遺傳算法采用非支配篩選方法，對目標函數優化問題進行求解，最終得到帕雷托優化解。

2.1 非支配篩選方法

本文采用的非支配解篩選方法是由Goldberg[11]最先提出的，現實中很多設計的優化算法都在使用該方法。本算法主要是對群體中的個體與其它個體進行比較，從而決定其非支配性。當發現第一個前沿，就會從主群體隔離其它非支配性個體，程序也會對后面的前沿不斷運行。通過對比群體中的個體與前沿中的非支配性個體，可以得到一個篩選流程：（1）得到群體(pop)；（2）將前沿P*中的第一個個體{ind(1)}列為P*(1)，讓P*_size=1；（3）用P*中的{P*(K)，K=1，P*_size}比較群體中的其它個體{ind(j), j=2, Pop_size)}；如果 ind(j)＜P*(K) ，將P*(K)替換為ind(j)；如果P*(K)＜ind(K)，j=j+1，繼續比較；否則，把ind(j)列為P*中的一部分，P*_size = P*_size+1，j=j+1，繼續比較；（4）結束前沿P*。

從篩選程序可知，如果在P*中沒有找到更多的非支配解的數目，那么就會一直增加。在此過程中，以前找到的P*中其它非支配個體將會從主群體中移走，搜尋另一個前沿的篩選流程又一次被完成。不斷重復執行流程，一直到整個群體被分配到不相同的前沿中。

2.2 遺傳算法

遺傳算法既可以在非支配篩選流程中應用，也可以在ε淘汰多樣性保持方法中應用，ε淘汰的程序代碼如程序1所示。

程序1 ε淘汰的代碼

在采用遺傳算法前，先建立一個隨機種群，如程序2所示。然后，基于ε淘汰程序算法，去除ε中相似個體，種群整體數目將會不斷減少。在此過程中，隨機產生的個體，對種群進行重新填充，這樣產生的搜索結果會更加有效。緊接著，非支配篩選程序將會對整個種群重新篩選，主要種群由得到的前沿結果組成。

程序2 遺傳算法

3 車輛振動模型目標函數優化

本文采用五自由度車輛模型，如圖1所示。M1代表前輪質量，m2代表后輪質量，mc代表座椅質量，ms代表簧載質量，Is代表簧載質量的慣性動量，kp1代表前輪剛度系數，kp2代表后輪剛度系數，l1代表前輪相對于質心的距離，l2代表后輪相對于質心的距離，kss代表座椅剛度系數，ks1、ks2代表車輛懸掛剛度系數，Css代表座椅阻尼系數，Cs1、Cs2代表車輛懸掛阻尼系數，r代表座椅與質心的距離。圖1中的下標1和2表示車輛輪胎軸線。汽車在行駛過程中經過障礙的動態模型如圖2所示。

3.1 線性微分方程

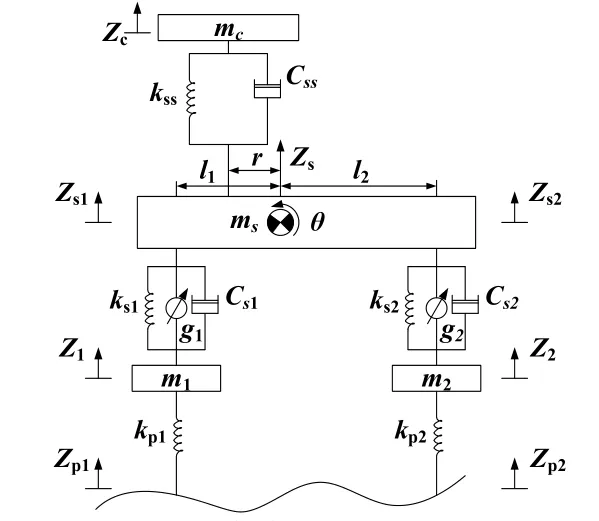
圖1 五自由度車輛振動模型

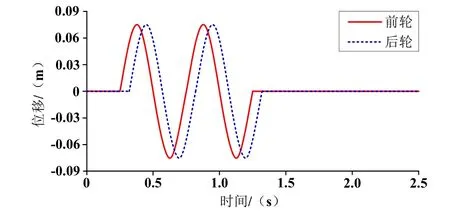
圖2 雙隆起物激勵

表1 模型的參數值

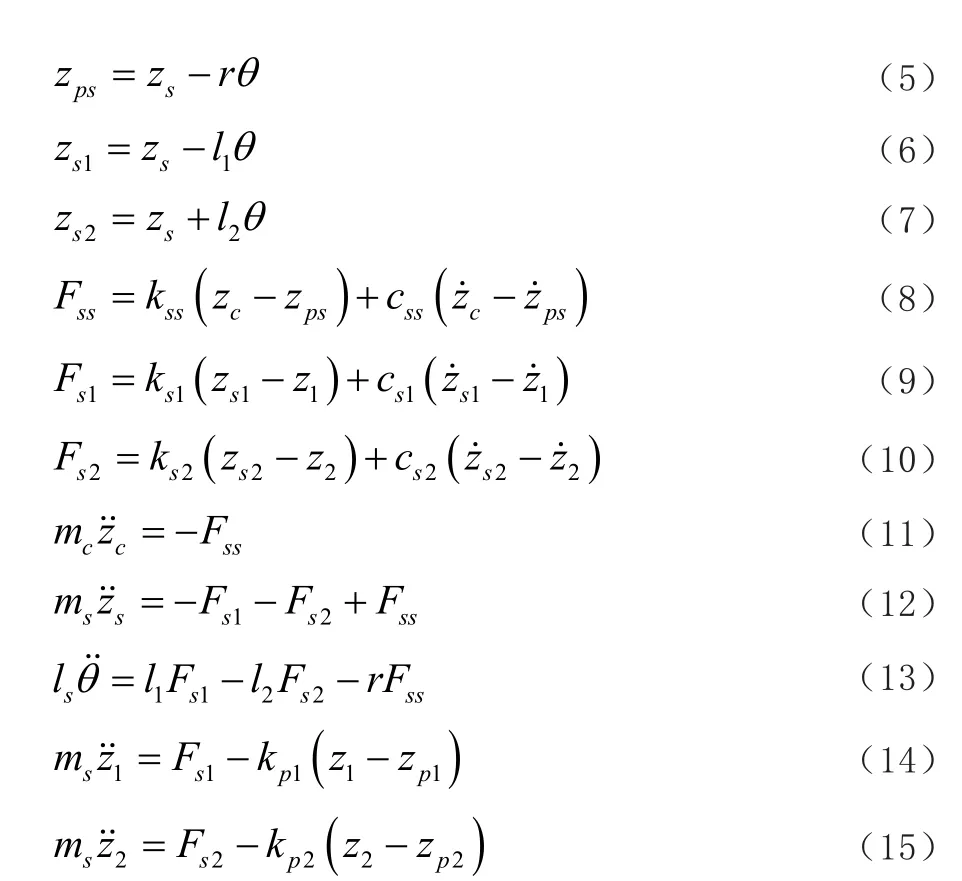
由文獻推導得到的五自由度和角度θ的線性運動微分方程公式如（5）～（15）所示。其中，zc代表座椅垂直位移，zs代表簧載質量重心的垂直位移，zsi代表簧載質量末端垂直位移，θ代表轉動角度，代表了座椅的垂直速度，代表輪胎垂直速度，代表簧載質量末端的垂直速度，代表座椅垂直加速度，代表簧載質量重心垂直加速度，代表輪胎垂直加速度，代表角加速度。

假設車輛行駛過程中經過圖2的障礙物，車輛速度恒定，v=20m/s。同時，后輪和前輪的運動軌跡相同，只是延遲一段時間，延遲量為△t=(lf+lv)/v。模型的振動參數值如表1所示。

在本研究中，60000≤kss≤160000、11000≤ks1≤21000、11000≤ks2≤21000、2000≤css≤5000、600≤cs1≤2100、600≤cs2≤2100及0≤r≤0.6，這些設計變量是針對5個不同目標函數：前輪速度、后輪速度、座椅加速度、前輪和簧載質量之間位移(d1)及后輪和簧載質量之間位移(d2)。

3.2 車輛振動優化

本文采用遺傳算法對車輛模型進行帕雷托優化，從5個目標函數中，選出4對不同的組合用于2-目標優化。為優化對象。假設種群中有90個個體，交叉概率為0.95，突變概率為0.2，種群使用了250代，對4對函數組成的優化處理如圖3～6所示。

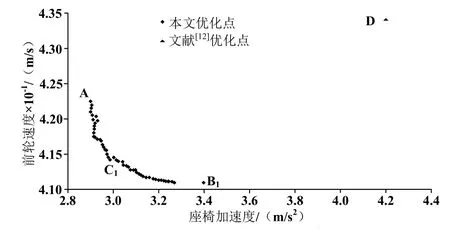
圖3 2-目標優化前輪速度與座椅加速度點

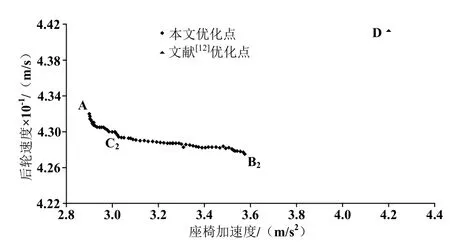
圖4 2-目標優化后輪速度與座椅加速度點

圖5 2-目標優化前輪位移與座椅加速度點

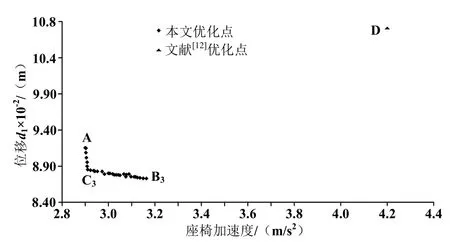
圖6 2-目標優化后輪位移與座椅加速度點

由圖3～6中可以得到，在進行一個目標函數優化時，優化得到的良好值通常會導致另一個目標函數值變差。但是，如果優化的決策變量的解集是采用帕雷托優化的方法來選擇，就可以得到一對優良的目標函數組合。也就是說，如果在優化過程中不采用此決策變量，所得到的目標函數優化值就會比相應的帕雷托優化得到的點值差。目標函數優化的差值一般位于右側或頂側。

在圖3中，點A代表座椅加速度的最佳值，點B1代表前輪速度的最佳值。在本文中，設計點優化得到的B1和C1對比顯示，座椅加速度隨著前輪速度的增長而降低，從B1到C1大約降低了10%。通過非支配帕雷托優化目標函數得到的結果如圖4～6所示。B2代表最佳的后輪速度，B3代表最佳簧載質量和前輪相對位移，B4代表最佳簧載質量和后輪相對位移，C2、C3、C4是綜合考慮后的優化設計點。由圖4～6可以知道，從點B2到C2，座椅加速度值相對降低了17%，從點B3到C3，座椅加速度值相對降低了8%，從點B4到C4，座椅加速度值相對降低了19%。由圖3～6中可知，采用R.Zarfam[12]等人優化設計后得到的點D比本文帕雷托優化得到的點差。本文優化設計得到的點及參數值輸入到Matlab/simulation軟件中進行仿真，并與R.Zarfam[12]等人得出的優化點仿真結果進行對比，對比結果如圖7～10所示。

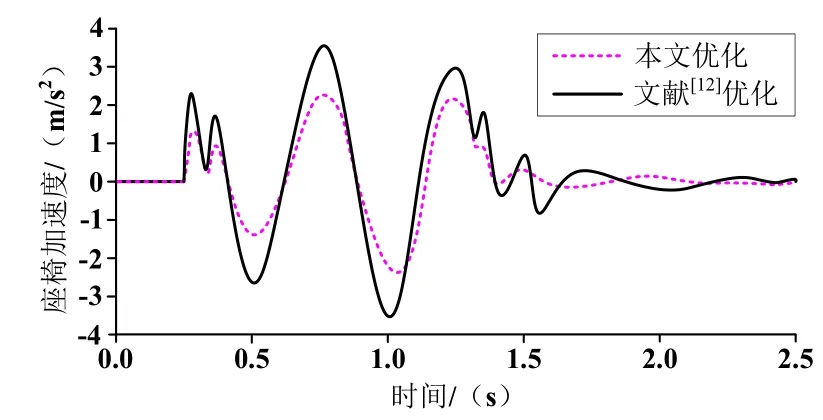
圖7 優化點C1、D座椅加速度仿真結果

圖8 優化點C2、D座椅加速度仿真結果

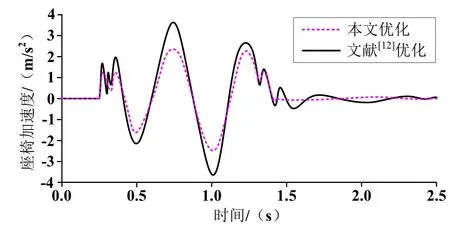
圖9 優化點C3、D座椅加速度仿真結果

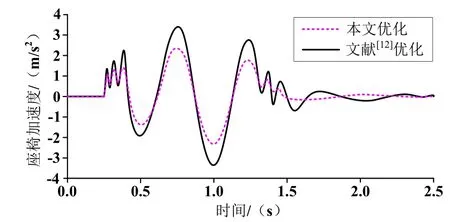
圖10 優化點C4、D座椅加速度仿真結果

從圖7～9可知，在同等條件下，本文中仿真的座椅加速度值比文獻要小。車輛在行駛過程中經過障礙物時，車輛振動相對較小，行駛過程相對平穩，舒適性較好。

4 結語

通過遺傳算法，對五自由度車輛振動模型的目標函數進行優化設計，主要包括以下五個變量：前輪速度、后輪速度、座椅加速度、簧載質量和前輪相對位移、簧載質量和后輪相對位移，并通過matlab/simulation軟件對優化結果進行仿真。同時，與其它文獻仿真結果進行對比。優化結果表明，汽車在行駛過程中經過障礙物時，座椅產生的加速度跳動較小，車輛振動較小，舒適性較好。

[1]劉波，王有志，安俊江，等.車輛—路面空間耦合振動模型及其動力響應分析[J].山東大學學報，2014，（3）：83-88.

[2]Paul D.Walker，Nong Zhang.Active Damping of Transient Vibration in Dual Clutchtransmission Equipped powertrains: A Comparison of Conventional and Hybrid Electric Vehi-cles[J].Mechanism and Machine Theory，2014，（77）：2-10.

[3]James Michael Hooper, James Marco.Characterising the in-vehicle Vibration Inputs to the High Voltage Battery of an Electric Vehicle[J].Journal of Power Sources，2014，（245）：511-518.

[4]Semih Sezer，Ali Erdem Atalay.Dynamic Modeling and Fuzzy Logic Control of Vibrations of a Railway Vehicle for Different Track Irregularities[J].Simulation Modelling Prac-tice and Theory，2011，（19）：1875-1892.

[5]張有為.車輛——軌道耦合系統高效隨機振動分析及優[D].大連：大連理工大學，2013.

[6]Eckardt Johanning.Vibration and Shock Exposure of Maintenance-of-way Vehicles in the Railroad Industry[J]. Applied Ergonomics，2011，（42）：556-561.

[7]曾銳.汽車動力傳動系扭振分析及其對車輛振動影響研究[D].成都：西南交通大學，2011.

[8]Le Thanh Danh， Kyoung Kwan Ahn.Active Pneumatic Vibration Isolation System Using Negative Stiffness Structures for a Vehicle Seat[J].Journal of Sound and Vibration，2014，（333）：1248-1265.

[9]Tadeusz Majewski.The Properties of a Dynamic Eliminator for Vehicle Vibrations[J].Mechanism and Machine Theory，2010，（45）：1450-1460.

[10]Ikbal Eski， Sahin Y1ld1r1m. Vibration Control of Vehicle Active Suspension System Using a New Robust Neural Network Control System[J].Simulation Modelling Practice and Theory，2009，（17）：780-790.

[11] Thilo Bein，Joachim B?s，Sven Herold.Smart Interfaces and Semi-active Vibration Absorber for Noise Reduction in Vehicle Structures[J].Science Direct，2008，（12）：63-72.

[12]R. Zarfam，A.R.Khaloo.Vibration Control of Beams on Elastic Foundation under a Moving Vehicle and Random Lateral Excitations[J].Journal of Sound and Vibration，2012，（331），1220-1230.

Optimization and Simulation of the Objective Function of Vehicle Vibration Model Based on Genetic Algorithm

GUO Weidong
(Nanjing Communications Institute of Technology,Nanjing 211188)

This a rticle from the perspective of genetic algorithms, the objective fu nction of optimization of vehicle vibration model. Meanwhile, theoretical results and previous studies were analyzed. Firstly, we are given the geneticalgorithm program objective fun ction of vehicle vibration model, taking into account the correlation function. Next, create a vehicle vibration model, while optimizing the objective function of correlation, taking 2- objective optimization front wheel s peed of the vehicle, the rear wheel velocity, acceleration of the se at, sprung mass, re lative displacement of the relative displacement of the front wheels and the rear wheels. F inally, the goal of optimizing the results by matlab software si mulation, the simulation results with previous results were analyzed. After optimization simulation results show that adopt a multi-objective genetic algorithm to optimize the vehicle vibration model, after the vehicle during the ground obstacles, sea t vibration is rel atively small, comfortable and good.

genetic algorithm,vehicle vibration,optimization, simulation