具有校正項(xiàng)的K分布形狀參數(shù)的V-估計(jì)器

李大朋

(中國(guó)科學(xué)院 光電研究院，北京100094)

迄今，人們提出了許多K分布形狀參數(shù)的估計(jì)方法(見(jiàn)文獻(xiàn)［1-9］).其中，極大似然估計(jì)方法(MLE)理論上給出了最優(yōu)的v參數(shù)估計(jì)［10］.不過(guò)，由于MLE的估計(jì)過(guò)程涉及冗繁的、十分低效的二維數(shù)值計(jì)算，一般不具有實(shí)際應(yīng)用價(jià)值.因此，計(jì)算比較簡(jiǎn)單的矩估計(jì)(MOM)就成了對(duì)v參數(shù)估計(jì)的最常用的方法.

在眾多矩估計(jì)器中，比較典型的是Oliver提出的U，V和W 3種K分布形狀參數(shù)估計(jì)器［11］.

眾所周知，估計(jì)器的性能由兩個(gè)因素決定:一是估計(jì)的精確性即估計(jì)精度，二是計(jì)算的復(fù)雜程度即估計(jì)效率.Blacknell［12］分析了 U，V 和 W 估計(jì)器的精度，得到的結(jié)論是U估計(jì)器的估計(jì)精度最高.但估計(jì)器U和W對(duì)形狀參數(shù)v的關(guān)系式是非線性函數(shù)，轉(zhuǎn)換時(shí)需要很大的計(jì)算量;而V-估計(jì)器可直接求得對(duì)v的估計(jì)值，則從估計(jì)求解的復(fù)雜性來(lái)看，V-估計(jì)器的估計(jì)效率最高.

另外，在實(shí)踐中人們發(fā)現(xiàn)，V-估計(jì)器估計(jì)精度不高的另一不良現(xiàn)象是，估計(jì)結(jié)果有時(shí)會(huì)出現(xiàn)異常大的奇異值，甚至出現(xiàn)v＜0等實(shí)際中不可能出現(xiàn)的誤估計(jì)情況.這些問(wèn)題的出現(xiàn)嚴(yán)重影響了V-估計(jì)器在實(shí)際中的應(yīng)用.

自O(shè)liver提出U，V和W估計(jì)器以來(lái)，人們一直在致力于探索出一種對(duì)K分布形狀參數(shù)v進(jìn)行估計(jì)的同時(shí)具有高精度、高效率的新型矩估計(jì)器，至今未見(jiàn)明顯進(jìn)展.

本文提出一種具有校正項(xiàng)的V-估計(jì)器，它克服了前述V-估計(jì)器的缺點(diǎn)，既保持了與V-估計(jì)器相同的估計(jì)效率，同時(shí)又具有很高的估計(jì)精度.仿真實(shí)驗(yàn)表明，從估計(jì)效率以及估計(jì)均值、估計(jì)偏差和估計(jì)標(biāo)準(zhǔn)差3方面的綜合考慮，這種帶校正項(xiàng)的V-估計(jì)器優(yōu)于U-估計(jì)器.

1 對(duì)V-估計(jì)器的改進(jìn)

1.1 V-估計(jì)器及其偏差分析

1993年，Oliver［11］提出了3 種著名的 K 分布形狀參數(shù)的矩估計(jì)器.其中的V-估計(jì)器(VE)形式如下:

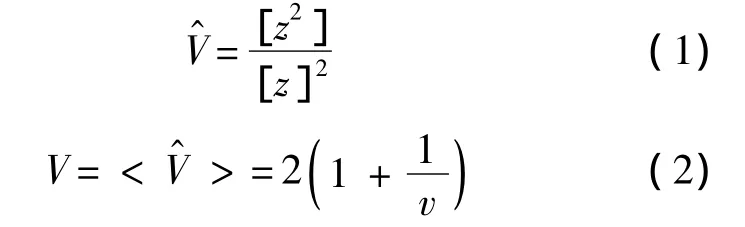
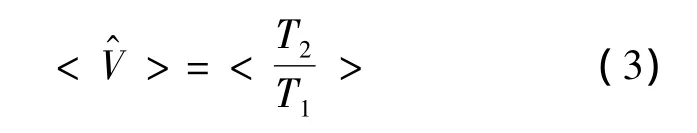
其中

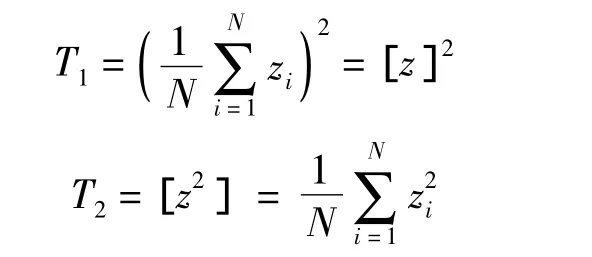
把1/T1=1/［z］2在它的均值點(diǎn) ＜z＞ 處展開(kāi)直到含有1/N項(xiàng)，則得

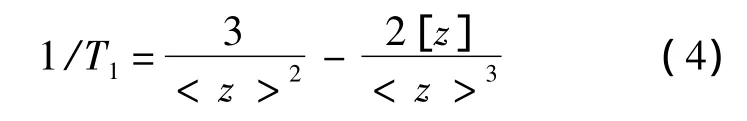
設(shè)ΔV為V-估計(jì)器的偏差，則借助式(4)有

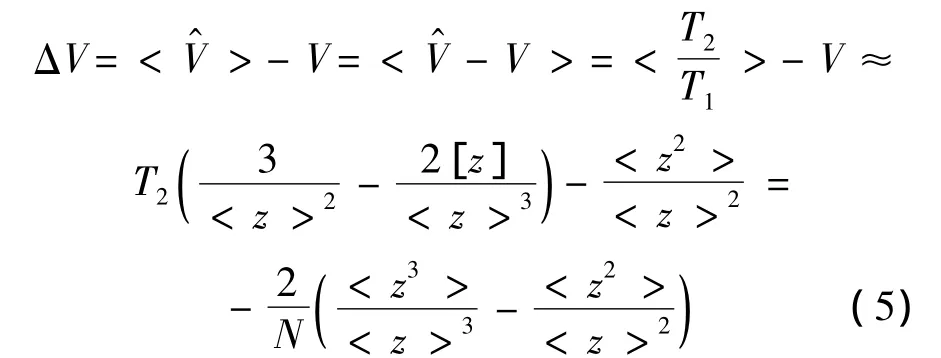
即得

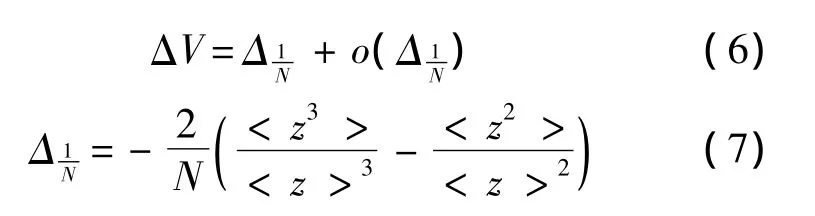
中的ΔN1為校正項(xiàng).由式(5)、式(6)可得

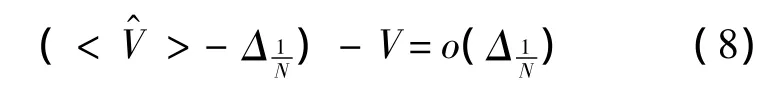
1.2 校正項(xiàng)和校正系數(shù)

為進(jìn)一步提高估計(jì)精度，借鑒文獻(xiàn)［13-14］通過(guò)實(shí)驗(yàn)手段，用經(jīng)驗(yàn)值來(lái)確定估計(jì)器公式中待定常數(shù)的方法，現(xiàn)給出具有校正項(xiàng)的 V-估計(jì)器(VCE)的表達(dá)式如下:其中，常數(shù)j稱(chēng)為校正系數(shù)，其確定方法見(jiàn)1.3節(jié).以下先給出式(10)的證明:由式(7)，顯然有，注意到式(5)和式(6)，則

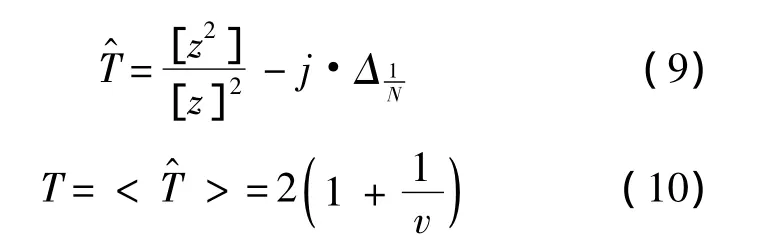
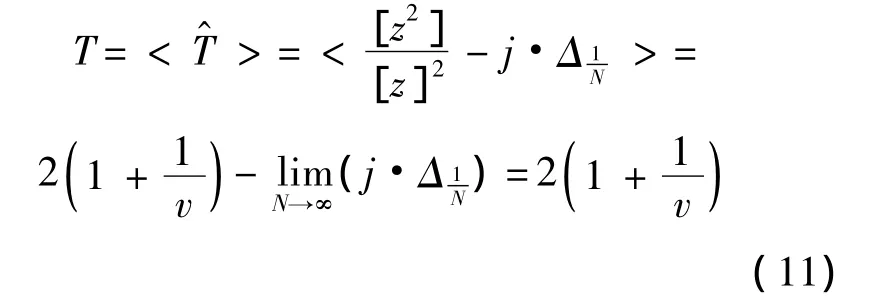
1.3 校正系數(shù)的確定

眾所周知，對(duì)于K分布形狀參數(shù)v，v∈［0.2，2］的范圍具有突出的重要意義.這是因?yàn)椋怆s波對(duì)雷達(dá)信號(hào)處理的影響很大，特別是在尖雜波背景下進(jìn)行恒虛警處理時(shí)，通過(guò)估計(jì)器估計(jì)得到的形狀參數(shù)v值的大的誤差，會(huì)造成虛警概率的急劇升高而引起大的信噪比損失［15］.所以，在實(shí)際的雷達(dá)信號(hào)處理中，人們更加注意尖雜波參數(shù)v∈［0.2，2］的范圍.基于此，本文以 v∈［0.2，2］的范圍為重點(diǎn)來(lái)確定校正系數(shù)j的滿(mǎn)足實(shí)際應(yīng)用的取值.

實(shí)驗(yàn)表明，校正系數(shù)j具有顯著地調(diào)節(jié)VCE的估計(jì)均值、偏差和標(biāo)準(zhǔn)差的作用.搜索校正系數(shù)j的實(shí)驗(yàn)是在［－3，3］的范圍內(nèi)以0.1為步長(zhǎng)進(jìn)行的.為便于說(shuō)明，圖1僅給出校正系數(shù)j分別取值0，1，2，2.5 和 3 情況下，相應(yīng)估計(jì)器同時(shí)經(jīng)10000次Monte-Carlo實(shí)驗(yàn)，所得估計(jì)均值的比較圖.實(shí)驗(yàn)條件:樣本長(zhǎng)度N=250，K分布形狀參數(shù)v∈［0.2，2］，實(shí)驗(yàn)步長(zhǎng)為 0.2.由圖1可見(jiàn)，校正系數(shù)j=2.5時(shí)的估計(jì)均值最好，故取校正系數(shù)j=2.5.需指出，j=0時(shí)的 VCE其實(shí)就是 VE即Oliver提出的V-估計(jì)器，而其在實(shí)驗(yàn)中所得均值遠(yuǎn)偏離j=2.5時(shí)的VCE得到的近乎理想的情況.這一事實(shí)驗(yàn)證了VCE中校正項(xiàng)和校正系數(shù)的突出作用.

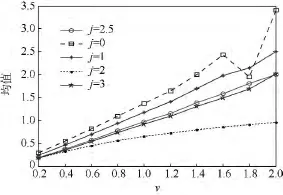
圖1 在估計(jì)器VCE中，校正系數(shù)j取不同值所得估計(jì)均值比較Fig.1 Comparison of estimating mean value obtained by the VCE for different corrective coefficient j

圖2給出在同一實(shí)驗(yàn)中，校正系數(shù)j取不同值所得估計(jì)偏差的比較.

圖2凸顯了VCE的優(yōu)越性:在校正系數(shù)j=2.5時(shí)，VCE對(duì)K分布形狀參數(shù)v估計(jì)的偏差仍然顯著優(yōu)于j取值的其他情況，遠(yuǎn)優(yōu)于包括j=0時(shí)的VCE即V-估計(jì)器得到的估計(jì)偏差.十分可貴的是，圖2中大多數(shù)估計(jì)器所得估計(jì)偏差呈現(xiàn)隨著v增大而增大的不良趨勢(shì)，而j=2.5時(shí)的VCE的估計(jì)偏差卻呈現(xiàn)隨著v增大而減小的良好趨勢(shì)并等于或接近于0.

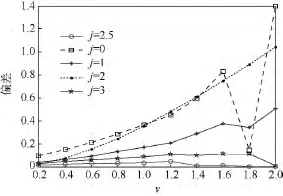
圖2 在估計(jì)器VCE中，校正系數(shù)j取不同值所得估計(jì)偏差比較Fig.2 Comparison of estimating bias obtained by the VCE for different corrective coefficient j

圖3給出在同一實(shí)驗(yàn)中，校正系數(shù)j取不同值所得估計(jì)標(biāo)準(zhǔn)差的比較.

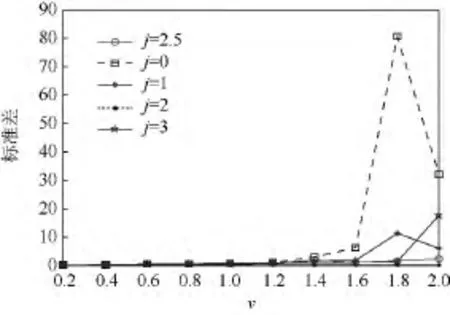
圖3 在估計(jì)器VCE中，校正系數(shù)j取不同值所得估計(jì)標(biāo)準(zhǔn)差比較Fig.3 Comparison of estimating standard error obtained by the VCE for different corrective coefficient j

從圖3粗看起來(lái)，似乎j=2時(shí)的VCE所得標(biāo)準(zhǔn)差精度最好.但實(shí)際是，從圖1、圖2易見(jiàn)，j=2時(shí)的VCE所得均值和偏差精度卻最低.j=3也有類(lèi)似情況.所以，從估計(jì)均值、估計(jì)偏差和估計(jì)標(biāo)準(zhǔn)差全面衡量，VCE中的校正系數(shù)j=2.5最為合適.而且，從圖3可以看到，j=0時(shí)的VCE即V-估計(jì)器得到的估計(jì)標(biāo)準(zhǔn)差在v=1.6處出現(xiàn)了奇異情況.這再次驗(yàn)證了VCE中校正項(xiàng)和校正系數(shù)對(duì)提高估計(jì)精度的顯著作用.

由此，必須強(qiáng)調(diào)，以后本文所指VCE就是校正系數(shù)j=2.5時(shí)的VCE.

2 仿真實(shí)驗(yàn)

圖4～圖6給出了通過(guò)仿真實(shí)驗(yàn)，VE，VCE和U估計(jì)器在估計(jì)均值、偏差和標(biāo)準(zhǔn)差3個(gè)方面的比較.

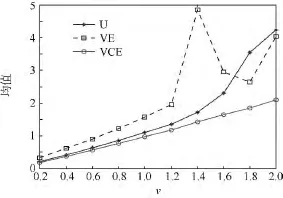
圖4 U，VE和VCE估計(jì)器所得對(duì)v的估計(jì)的均值比較Fig.4 Comparison of mean value for estimating v obtained by U，VE and VCE

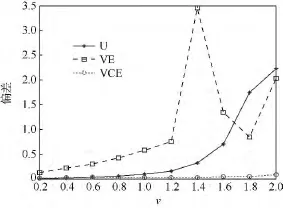
圖5 U，VE和VCE估計(jì)器所得對(duì)v的估計(jì)的偏差比較Fig.5 Comparison of bias for estimating v obtained by U，VE and VCE

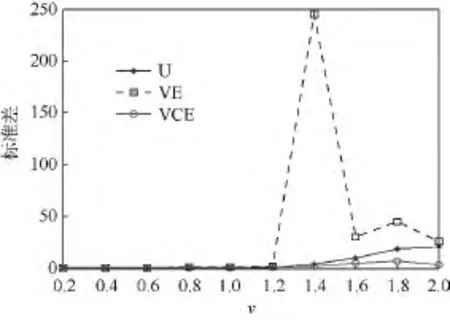
圖6 U，VE和VCE估計(jì)器所得對(duì)v的估計(jì)的標(biāo)準(zhǔn)差比較Fig.6 Comparison of standard error for estimating v obtained by U，VE and VCE

實(shí)驗(yàn)條件:樣本長(zhǎng)度N=100，K分布形狀參數(shù) v∈［0.2，2］，實(shí)驗(yàn)步長(zhǎng)為 0.2，10000次 Monte-Carlo實(shí)驗(yàn).

圖4～圖6表明，在重要的 v∈［0.2，2］的v值范圍內(nèi)，從估計(jì)均值考慮，VCE的估計(jì)均值的精度顯著優(yōu)于U-估計(jì)器，更是優(yōu)于VE;而從估計(jì)偏差考慮，VCE的估計(jì)偏差的精度同樣是明顯優(yōu)于VE，并且隨著v值的增大，越來(lái)越更加優(yōu)于U-估計(jì)器;再?gòu)墓烙?jì)的標(biāo)準(zhǔn)差考慮，VCE在v∈［0.2，1.2］范圍內(nèi)，估計(jì)標(biāo)準(zhǔn)差的精度基本等于U-估計(jì)器的精度，卻仍然遠(yuǎn)高于VE的估計(jì)精度.而在 v∈［1.2，2］的范圍內(nèi)，即隨著 v值的增大，所得標(biāo)準(zhǔn)差卻越來(lái)越明顯好于U-估計(jì)器.于是，從估計(jì)均值、估計(jì)偏差和估計(jì)標(biāo)準(zhǔn)差3方面的精度情況全面考慮，應(yīng)該認(rèn)為，實(shí)驗(yàn)中VCE在估計(jì)精度上不但顯著優(yōu)于VE，同時(shí)也優(yōu)于U-估計(jì)器.而從估計(jì)的效率考慮，VCE和VE一樣，具有估計(jì)過(guò)程中不需要求解非線性方程，直接給出對(duì)v的估計(jì)值的高效率，這是包括U-估計(jì)器在內(nèi)的，必須通過(guò)求解非線性方程進(jìn)行估計(jì)的所有矩估計(jì)器所無(wú)法具有的突出優(yōu)點(diǎn).

需指出，圖1～圖3的實(shí)驗(yàn)結(jié)果是在樣本長(zhǎng)度N=250的條件下得到的，而圖4～圖6的實(shí)驗(yàn)結(jié)果是在樣本長(zhǎng)度N=100的情況下獲得的.因此，有關(guān)仿真實(shí)驗(yàn)還表明了這樣一個(gè)可貴事實(shí):不論是在大樣本情況下還是在小樣本情況下，VCE的估計(jì)精度具有對(duì)樣本長(zhǎng)度的較為廣泛的適應(yīng)性.相反，由圖4～圖6的實(shí)驗(yàn)可見(jiàn)，VE與U估計(jì)器對(duì)小樣本情況的適應(yīng)性是比較差的.

3 結(jié)論

1)本文提出的具有校正項(xiàng)的V估計(jì)器VCE，在保留與VE同樣高的估計(jì)效率的同時(shí)，顯著提高了估計(jì)的精度，在估計(jì)均值、估計(jì)偏差和估計(jì)標(biāo)準(zhǔn)差3個(gè)方面全面明顯超過(guò)VE估計(jì)器.

2)仿真實(shí)驗(yàn)表明，本文提出的具有校正項(xiàng)的V-估計(jì)器VCE，在小樣本情況下，對(duì)K分布形狀參數(shù)v估計(jì)的精度與效率都優(yōu)于U-估計(jì)器.VCE對(duì)樣本長(zhǎng)度有著較為廣泛的適應(yīng)性，更便于在實(shí)踐中應(yīng)用.

References)

［1］ Blacknell D，Tough R J A.Parameter estimation for the K-distribution based on［z log(z)］［J］.IEE Proceedings:Radar，Sonar and Navigation，2001，148(6):309-312.

［2］ 李永晨，劉瀏.SAR圖像統(tǒng)計(jì)模型綜述［J］.計(jì)算機(jī)工程與應(yīng)用，2013，49(13):184-190.Li Y C，Liu L.Review of statistical method of SAR image［J］.Computer Engineering and Applications，2013，49(13):184-190(in Chinese).

［3］ 孫增國(guó).基于第二類(lèi)統(tǒng)計(jì)量的K分布參數(shù)估計(jì)［J］.計(jì)算機(jī)應(yīng)用研究，2013，30(1):1-4.Sun Z G.Parameter estimation of K distribution based on secondkind statistics［J］.Application Research of Computers，2013，30(1):1-4(in Chinese).

［4］ 李亞超，周瑞雨，全英匯，等.自適應(yīng)背景窗的艦船目標(biāo)檢測(cè)算法［J］.西安交通大學(xué)學(xué)報(bào)，2013，36(3):1-6.Li Y C，Zhou R Y，Quan Y H，et al.An algorithm of ship target detection based on the adaptive background window function［J］.Journal of Xi’an Jiaotong University，2013，36(3):1-6(in Chinese).

［5］ 楊永生，張宗杰.基于分?jǐn)?shù)階矩和NM單純形算法的海雜波參數(shù)估計(jì)［J］.遙感技術(shù)與應(yīng)用，2011，25(6):70-73.Yang Y S，Zhang Z J.Parameters estimation of sea clutter based on fractional order moments and NM algorithm［J］.Remote Sensing Technology，2011，25(6):70-73(in Chinese).

［6］ 徐偉，陳永森.一種K分布雜波參數(shù)估計(jì)方法［J］.艦船電子對(duì)抗，2013，36(3):89-91.Xu W，Chen Y S.An estimation method for K-distribution clutter parameters［J］.Shipboard Electronic Countermeasure，2013，36(3):89-91(in Chinese).

［7］ 胡文琳，王永良，王首勇.基于zrlog(z)期望的K分布參數(shù)估計(jì)［J］.電子與信息學(xué)報(bào)，2008，30(1):203-205.Hu W L，Wang Y L，Wang S Y.Estimation of the parameters K-distribution based on zrlog(z)［J］.Journal of Electronics＆ Information Technology，2008，30(1):203-205(in Chinese).

［8］ 李大朋，姚迪.對(duì)Jahangir組合式矩估計(jì)器的改進(jìn)［J］.北京航空航天大學(xué)學(xué)報(bào)，2012，38(6):788-792.Li D P，Yao D.Improvement of Jahangir’s multiple moments estimator［J］.Journal of Beijing University of Aeronautics and Astronautics，2012，38(6):788-792(in Chinese).

［9］ 李大朋，姚迪.對(duì)K分布形狀參數(shù)M估計(jì)器的再改進(jìn)［J］.電子與信息學(xué)報(bào)，2011，33(7):1752-1755.Li D P，Yao D.A further enhanced M-estimator for the K-distribution shape parameter［J］.Journal of Electronics ＆ Information Technology，2011，33(7):1752-1755(in Chinese).

［10］ Joughin I R.Maximum likelihood estimation of K-distribution parameters for SAR data［J］.IEEE Trans on Geosciences and Remote Sensing，1993，31(5):989-999.

［11］ Oliver C J.Optimum texture estimators for SAR clutter［J］.Journal of Physics D:Applied Physics，1993，26(11):1824-1835.

［12］ Blacknell D.Comparison of parameter for K-distribution［J］.IEE Proceedings:Radar，Sonar and Navigation，1994，141(1):45-52.

［13］ Jahangir M，Blacknell D，White R G.Accurate approximation to the optimum parameter estimate for K-distributed clutter［J］.IEE Proceedings:Radar，Sonar and Navigation，1996，143(6):383-390.

［14］ 郝程鵬，侯朝煥.一種K-分布雜波背景下的雙參數(shù)恒虛警檢測(cè)器［J］.電子與信息學(xué)報(bào)，2007，29(3):756-759.Hao C P，Hou C H.A two parameter CFAR detector in K-distribution clutter［J］.Journal of Electronics ＆ Information Technology，2007，29(3):756-759(in Chinese).

［15］ 郝程鵬，侯朝煥，鄢錦.一種新的 K分布形狀參數(shù)估計(jì)器［J］.電子與信息學(xué)報(bào)，2005，27(9):1404-1407.Hao C P，Hou C H，Yan J.A new estimator for estimating the parameters of K-distribution［J］.Journal of Electronics ＆ Information Technology，2005，27(9):1404-1407(in Chinese).