一種變體飛行器的動力學建模與動態特性分析

張杰，吳森堂

(北京航空航天大學 自動化科學與電氣工程學院，北京100191)

近年來軍用和民用航空對飛行器提出了越來越高的要求:飛行器既要適應飛行環境的變化、執行不同任務，又要保證飛行性能.顯然固定翼飛行器技術無法同時滿足這些要求.變體飛行器技術應運而生.變體飛行器指一種為了實現多任務飛行，大尺度地改變氣動外形的航空飛行器［1-3］.

在過去幾十年中，世界各國開展了大量與變體飛行器技術相關的研究.其中美國開展的研究數量最多、范圍最廣，主要有1979年的 AFTI/F111自適應機翼項目［4］，1985年的主動柔性機翼(AFW)計劃［5］，1995 年的智能機翼項目［6］，以及2003年的變體飛行器結構(MAS)項目［3］，這些研究計劃在針對變體飛行器的氣動性能、結構設計、控制技術、智能材料、多學科綜合技術等方面進行了很多理論分析與試驗，取得了很多有價值的成果.國內為數不多的單位在變體飛行器的氣動機理、材料與結構、動力學建模和控制等方面也取得了一定的成果［7-10］.

由于變體飛行器需要在相當大的范圍內改變氣動外形，因此，不能像常規飛行器那樣將變體飛行器作為單個剛體進行動力學建模，而要建立一種包含變形結構的動力學模型.文獻［11］提出了一種變體飛行器的飛行力學建模方法，并在一種鷗翼飛行器中進行了仿真驗證;文獻［12］針對大尺度變形的變體飛行器提出了一種動力學建模與飛行控制方法;文獻［13］為一種可變展長的飛行器建立了動力學模型.以上建模過程大多采用經典牛頓力學方法，把飛行器看作一個整體，求取其動量和對質心的動量矩，并對時間求導，進而建立飛行器在外合力F作用下的平移運動方程與在外合力矩M作用下的轉動運動方程.

本文將可變展長、變后掠角的變體飛行器簡化為一個多剛體系統，采用Kane方法建立其動力學模型，使方程中不出現積分項以及對慣性矩的求導項.基于此動力學模型，分析了變體運動對飛行器產生的附加動力學影響，并對變體過程中飛行器的縱向運動響應進行了仿真分析.

1 Kane方法

對于非完整系統，Kane方法選取f(f為系統的自由度數)個獨立的廣義速度的線性組合作為系統的獨立變量，描述系統的運動，稱該線性組合為廣義速率，記作 uk(k=1，2，…，f).

uk確定后，系統中任意剛體相對于慣性參考系的質心速度vci以及轉動角速度ωi均可唯一地表示為廣義速率的線性組合:

對于具有N個剛體和f個自由度的多剛體系統，Kane方程在慣性參考系里的表達式為［14］

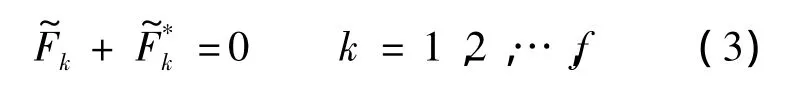
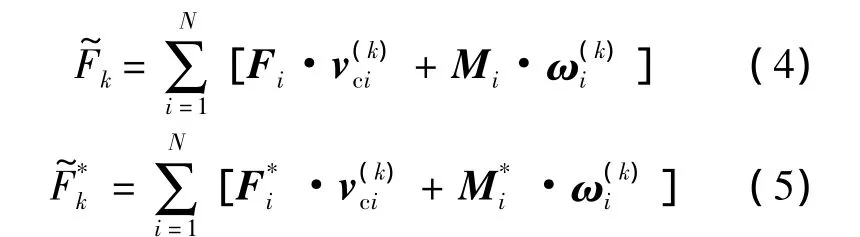
式中，Fi和Mi分別為作用在剛體i上的主動力的主矢和相對質心的主矩;F*i和M*i分別為剛體i的慣性力主矢和相對質心的主矩，可以用以下公式求出:

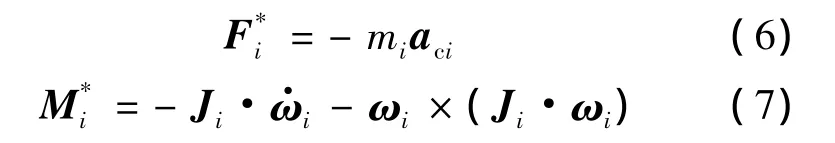
式中，Ji為剛體i的慣量張量;aci為剛體i質心的加速度.

2 物理模型

假設飛行器由5個獨立剛體組成(見圖1):機身、左翼內側、左翼外側、右翼內側以及右翼外側，質量分別為 mb，m1，m2，m1，m2，總質量為 mt.

機身簡化為一個均質柱體1，半徑為R，長度為l，質心為Cb.每個機翼簡化為兩個均質細桿的組合:左側機翼為桿2與桿3的組合，其中桿2以A為軸相對機身進行轉動，桿3沿桿長方向相對于桿2做直線伸縮運動;右側機翼為桿4與桿5的組合.設機翼內側桿的長度為l1，機翼外側桿的長度為 l2.左、右機翼后掠角分別為 θ1，θ2;左、右機翼的外側相對內側的伸出長度分別為Δ1，Δ2.設機翼簡化后的桿與機身的對稱軸位于同一平面內，亦為機身的縱向慣量主軸平面.

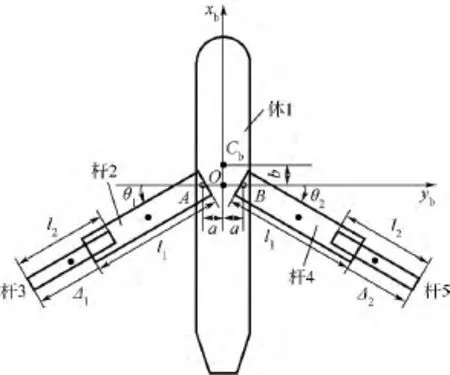
圖1 飛行器簡化模型Fig.1 Morphing aircraft’s simplified model

假設地面坐標系Ogxgygzg為慣性系，zg軸垂直向下指向地心.機體坐標系Oxbybzb以A，B連線的中點O為原點，xb軸沿體1的中心慣量主軸指向機頭，yb軸垂直于xb軸指向機身右方，zb軸按右手法則指向機體下方.

3 變體飛行器動力學建模

3.1 廣義坐標與廣義速率

假設機翼相對于機身的變形運動可以通過變體控制機構進行有效控制，這樣一個給定的變形過程可以用一組約束方程表示:

式中，X為機翼變形運動的狀態向量，包括機翼的展長與后掠角的位置、速度以及加速度;Xr為狀態向量的給定值.

約束方程(8)可以有效地表示變體飛行器機翼變形運動的相關自由度.給定約束方程(8)，系統的獨立自由度就可以取為機身空間運動的6個自由度.

選取機身上O點在地面坐標系中的坐標x，y，z以及機體坐標系相對于地面坐標系的俯仰角θ、滾轉角φ、偏航角ψ 6個變量作為系統的廣義坐標.選取O點在地面坐標系中平移運動的速度V 在 xb，yb，zb軸上的分量 u，v，w，以及機體坐標系相對于地面坐標系轉動運動的角速度ω在xb，yb，zb軸上的分量p，q，r 6個變量作為系統的廣義速率，即 uk(k=1，2，…，6)分別為 u，v，w，p，q，r.

以機體坐標系為參考系求解各剛體相對于慣性系的質心速度vci和轉動角速度ωi.各剛體的質心加速度aci、繞質心的角加速度可直接由vci，ωi對時間求導得到.利用式(1)、式(2)可以得出各剛體的質心偏速度和偏角速度

3.2 廣義主動力與廣義慣性力

給定約束方程(8)，可以把機翼與機身之間以及機翼內、外側之間的相互作用力當作系統的約束力，在Kane方程中不顯含系統的約束力.變體飛行器所受到的外部主動力包括重力、空氣動力和發動機推力.本文建立的系統的自由度是機身的6個自由度，飛行器所受到的空氣動力的作用完全可以簡化到機身上，而不影響這些自由度運動的正確性，其他部分只受自身重力的作用.

假設機身所受到的發動機推力T的偏置角為零，即推力只有xb軸上的分量T.機體1受到的主動力和主動力矩在Oxbybzb中的表達式為

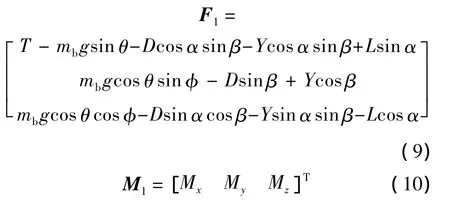
式中，D為阻力;Y為側力;L為升力;Mx為滾轉力矩;My為俯仰力矩;Mz為偏航力矩;α為攻角;β為側滑角.

系統中其余各剛體受到的主動力只有重力，主動力矩為零.廣義主動力和廣義慣性力分別由式(4)和式(5)計算得到.

3.3 構造Kane方程

根據式(3)可以得出飛行器的六自由度動力學模型，見附錄A.其中，式(A1)～式(A3)為對應于廣義速率 u，v，w的力平衡方程，式(A4)～式(A6)為對應于廣義速率p，q，r的力矩平衡方程.式(A1)、式(A3)、式(A4)為縱向動力學方程，式(A2)、式(A5)、式(A6)為橫側向動力學方程.

4 變體過程動態特性仿真分析

4.1 仿真平臺及參數

選用BQM-34“Firebee”無人靶機作為飛行器平臺，機翼改為可變展長變后掠的可變形機翼.BQM-34機翼的重量為全機總重量的7%［15］，考慮到變體機構對機翼重量的影響，取機翼的重量占全機總重量的15%，其中內側機翼重量是外側機翼重量的4倍.仿真參數見表1.

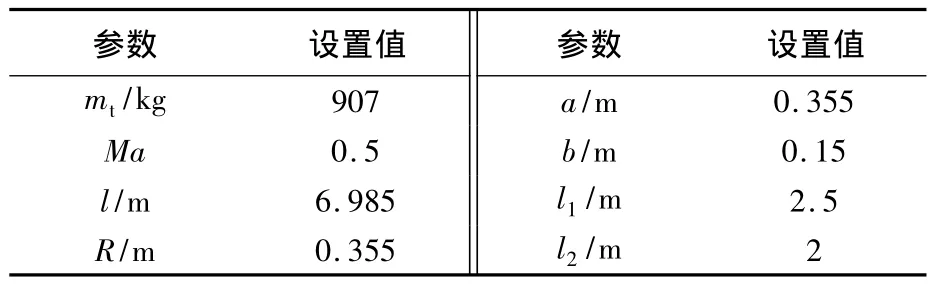
表1 基本仿真參數設置Table1 Parameters for simulation

采用的飛行器氣動外形參數如下:機翼內側與機翼外側的根梢比均為1;在后掠角為零時，機翼內側弦長為0.8 m，外側弦長為0.7 m.基于準定常假設，采用 Missile Datcom［16］軟件分別計算變體飛行器在4種氣動布局(見圖2)下的氣動參數，在后續的仿真中采用線性插值的方法得到其他外形相應的氣動數據.

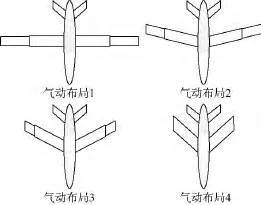
圖2 4種氣動布局Fig.2 Four aerodynamic configurations

計算結果表明，飛行器在變形前后的氣動系數變化較大，如在2°攻角下，從氣動布局1變形到氣動布局4，升力系數減小27.3%，因為在變形過程中，機翼的面積明顯減小.

4.2 變形運動產生的附加動力學影響分析

可變展長、可變后掠角的飛行器進行變形運動時，除了所受空氣動力會隨氣動外形的變化而改變外，還會產生源于變形運動的附加力和附加力矩的影響.附加力是指在力平衡方程中所有由變形運動引入的項(即含有的項，不包括空氣動力)的和，其在 xb，yb，zb軸上的分量分別記作 ΔFx，ΔFy，ΔFz.附加力矩是指在飛行器的力矩平衡方程中所有由變形運動引入的項(不包括空氣動力矩)的和，其在xb，yb，zb軸上的分量分別記作 ΔMx，ΔMy，ΔMz.附加力與附加力矩就是變形運動引起的機翼的慣性力與慣性力矩，也是變體飛行器動力學方程與固定翼飛行器動力學方程的主要區別.

下面通過兩組仿真來分析機翼變形過程中產生的附加力和附加力矩的特性.假設在變形過程中，飛行器的速度和姿態保持不變.

1)假設機翼左右對稱變形.

第1步:從氣動布局1變形到氣動布局4，變形過程為一階慣性環節，時間常數τ分別為1 s和15 s;

第2步:進行反向變形.結果見圖3.

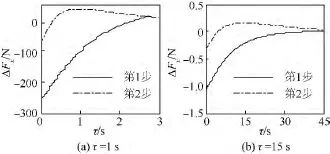
圖3 對稱一階變形附加力Fig.3 Additional force under symmetric first-order morphing

2)假設只有右側機翼變形.

第1步:從氣動布局1勻速變形到氣動布局4，變形時間為1 s;

第2步:進行反向變形.結果見圖4.

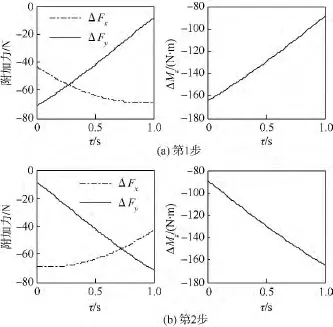
圖4 單側翼變形附加力及附加力矩Fig.4 Additional forces and moment under asymmetric morphing

由以上仿真結果可知，變形速度越快附加力就越大，τ為15 s時產生的附加影響基本可以忽略不計;對稱變形只會產生附加力ΔFx，ΔFx相對于飛行器所受重力來說較小，最大僅為重力的3%，因為機翼的質量在整個飛行器中的比重較小，且變形的絕對速度不大;非對稱變形還會對yb軸方向側力以及繞zb軸偏航力矩產生附加影響，這會影響飛行器的橫側向穩定性.

結合4.1節氣動特性參數的計算以及文獻［10］對變體飛行器非定常氣動特性的分析可知，在變形過程中，飛行器所受空氣動力的變化比所受附加力與附加力矩要大很多，前者對動力學特性的影響是最主要的，在變形速度不大時后者基本可以忽略.以上分析可為變體飛行器動力學模型的簡化提供參考依據.

4.3 變體引起的飛行器縱向運動響應分析

假設飛行器的結構是面對稱的，即θ1≡θ2，Δ1≡Δ2;飛行器進行無滾轉無側滑的飛行運動，即滿足條件φ=φ=β≡0，p=r≡0.對動力學模型進行解耦簡化，得到飛行器的縱向動力學模型.

對變體運動所引起的飛行器縱向運動響應進行仿真，變形過程為從氣動布局1勻速變形到氣動布局4，時間分別為1 s和15 s.初始條件是高度為10 km，0.5Ma的水平無側滑穩態飛行.

由圖5的仿真結果可知:當機翼開始變形，俯仰角速度變為負值，俯仰角逐漸變小，因為在機翼后掠的過程中，氣動中心逐漸后移從而產生了低頭力矩.變形開始后，飛行高度逐漸降低，飛行速度逐漸增加，因為隨著機翼的后掠和收縮，機翼面積逐漸減小，進而升力變小，其在垂直方向上的分量不足以平衡重力，同時隨著俯仰角的減小，發動機推力在垂直向上方向的分量減小，都會使飛行器獲得向下的加速度.飛行器垂直機身向下速度分量的增加，會導致攻角逐漸增加.

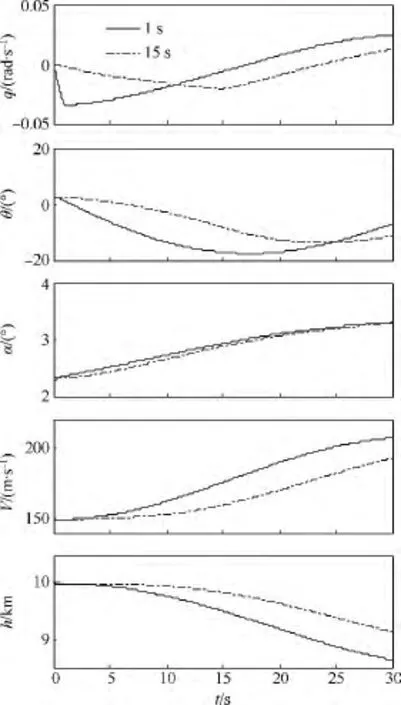
圖5 變體過程動態響應Fig.5 Dynamic responses during morphing

變形結束后，氣動中心停止后移，在配平舵偏角的作用下，俯仰角速度逐漸回復到零及正值，俯仰角由減小逐漸變為增加;升力還是不足以平衡重力，所以高度繼續下降.隨著高度的下降，飛行速度以及攻角的增加，升力會逐漸增加，直至平衡甚至大于重力，使得飛行器上升，經過較長的振蕩過程最終達到新的平衡狀態.變形后，機翼面積減小會使升力變小，所以新的平衡狀態下，飛行器的速度與攻角都會增大.對比兩種變形速度可知:變形速度越大，飛行器狀態變化越快，狀態的變化量也越大;變形結束后，不同變形速度帶來的影響會逐漸接近.

以上分析表明:針對變體飛行器的動態特性及其模型與氣動參數的不確定性，需要設計特定的魯棒控制系統，以使其在變體過程中保持穩定.

5 結論

1)簡化了可變展長、可變后掠角變體飛行器的物理模型，利用Kane方法建立了該種飛行器的動力學模型，可作為變體飛行器飛行控制系統設計與研究的基礎.

2)機翼對稱變形只會在xb軸方向產生附加動力學影響;非對稱變形還會對yb軸方向以及偏航力矩產生附加影響;但以上附加影響相對于空氣動力的變化來說較小，后者對變體過程的動力學影響是最主要的，該結果可用于動力學模型的簡化.

3)對變體引起的飛行器縱向運動響應的仿真表明:飛行器的高度、速度以及俯仰角均發生很大變化;變形速度越大，飛行器狀態的變化越快，其變化量也越大.

附錄A

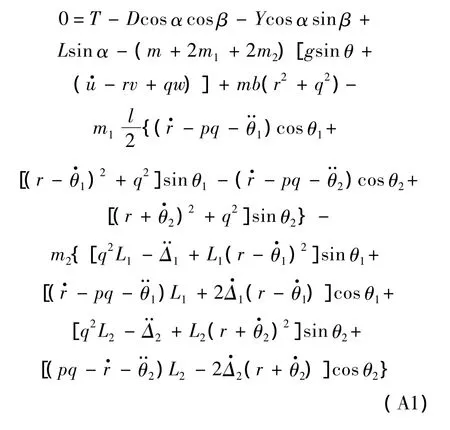
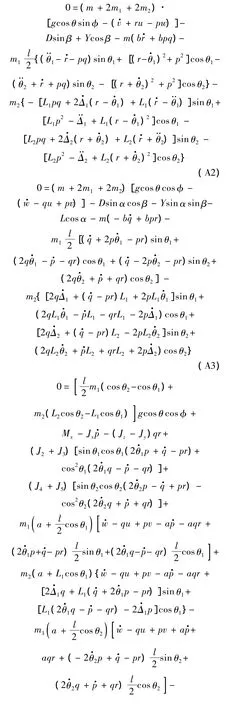
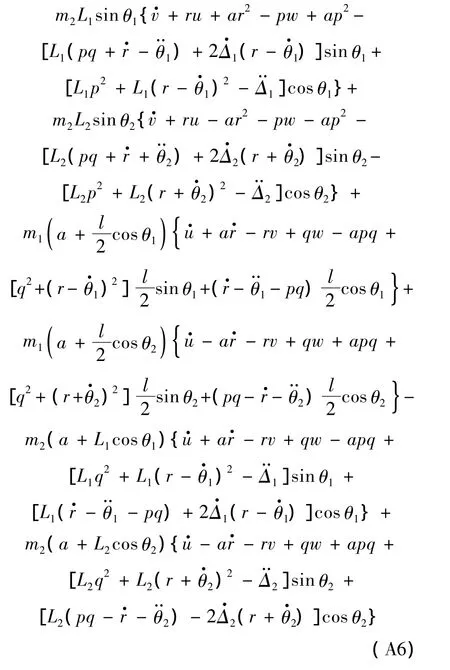
References)

［1］ Reich G，Sanders B.Introduction to morphing aircraft research［J］.Journal of Aircraft，2007，44(4):1059.

［2］ Barbarino S，Bilgen O，Ajaj R M，et al.A review of morphing aircraft［J］.Journal of Intelligent Material Systems and Structures，2011，22(9):823-877.

［3］ Weisshaar T A.Morphing aircraft technology-new shapes for aircraft design，RTO-MP-AVT-141［R］.France:DTIC Document，2006.

［4］ Bonnema K，Smith S.AFTI/F-111 mission adaptive wing flight research program［C］//4th Flight Test Conference.USA:AIAA，1988:155-161.

［5］ Pendleton E W，Bessette D，Field P B，et al.Active aeroelastic wing flight research program:technical program and model analytical development［J］.Journal of Aircraft，2000，37(4):554-561.

［6］ Kudva J N.Overview of the DARPA smart wing project［J］.Journal of Intelligent Material Systems and Structures，2004，15(4):261-267.

［7］ Yue T，Wang L X，Ai J Q.Gain self-scheduled H∞control for morphing aircraft in the wing transition process based on an LPV model［J］.Chinese Journal of Aeronautics，2013，26(4):909-917.

［8］ He Z，Lu Y P.Decentralized robust control design for spatially interconnected systems with uncertainties［J］.International Journal of Innovative Computing，Information and Control，2010，6(4):1763-1771.

［9］ 董二寶.智能變形飛行器結構實現機制與若干關鍵技術研究［D］.合肥:中國科學技術大學，2010.Dong E B.Research on realization mechanism and some key technologies of smart morphing aircraft structures［D］.Hefei:University of Science and Technology of China，2010(in Chinese).

［10］ 陳錢，白鵬，李鋒.飛行器變后掠過程非定常氣動特性形成機理［J］.力學學報，2013，45(3):307-313.Chen Q，Bai P，Li F.Study on the formatioin mechanisms of unsteady aerodynamic characteristics of morphing flight vehicle in sweep-varying process［J］.Chinese Journal of Theoretical and Applied Mechanics，2013，45(3):307-313(in Chinese).

［11］ Obradovic B，Subbarao K.Modeling of flight dynamics of morphing-wing aircraft［J］.Journal of Aircraft，2011，48(2):391-402.

［12］ Seigler T M，Neal D A，Bae J S，et al.Modeling and flight control of large-scale morphing aircraft［J］.Journal of Aircraft，2007，44(4):1077-1087.

［13］ Henry J J.A mathematical model for roll dynamics by use of a morphing-span wing［C］//48th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Conference.Reston:AIAA，2007:76-91.

［14］ 劉延柱.高等動力學［M］.北京:高等教育出版社，2001.Liu Y Z.Advanced dynamics［M］.Beijing:Advanced Education Press，2001(in Chinese).

［15］ Shiv J，Zeb T，William C，et al.Comparison of morphing wing stategies based upon aircraft performance impacts［C］//45th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics＆ Materials Conference.USA:AIAA，2004:1-7.

［16］ Bowman J，Sanders B，Weisshaar T.Evaluating the impact of morphing technologies on aircraft performance［C］//43rd AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Conference.USA:AIAA，2002:1-114.