蜂蠅懸停和前飛時的動穩定性

許娜，孫茂

(北京航空航天大學 航空科學與工程學院，北京100191)

近年來，隨著對昆蟲飛行空氣動力學機理的深入研究和認識，人們將目光更多地轉移到飛行動穩定性的研究上來［1-12］.昆蟲飛行中的擾動運動包括縱向和橫向兩種，通過對運動方程的線化處理，可將二者分開進行研究.對于昆蟲懸停的縱向穩定性的研究，目前已經做了大量的研究工作［1，3，6，8，11］.近年來，運用類似于縱向穩定性的處理方法，人們對昆蟲的橫向穩定性［9-11］也進行了一定的研究.通過對不同種類昆蟲穩定性的研究，昆蟲懸停時縱向和橫向穩定性已較為清楚，但昆蟲在前飛狀態下的穩定性研究較少;區別于懸停狀態，昆蟲在前飛時有自由來流，拍動平面傾角相對較大，翅膀在下拍時的攻角和相對速度與上拍時也有很大的不同.前飛和懸停在平衡狀態下運動參數的差異有可能導致二者氣動導數的不同，從而出現不同的穩定特性.文獻［7，12］分別研究了熊蜂前飛時縱向和橫向的穩定性，總結并分析了其與懸停時動穩定性的差異.而到目前為止，由于前飛數據缺乏的局限，昆蟲前飛的穩定性問題只有上述針對熊蜂開展的研究，其普適性也亟待驗證.因此，其他種類昆蟲前飛時的縱橫向動穩定性的研究工作仍具有重要意義.

本文選用具有相對完整前飛數據的蜂蠅為研究對象，應用平均模型理論和CFD方法計算其氣動導數，并運用特征模態分析方法研究蜂蠅懸停和前飛時的縱向和橫向動穩定性.

1 理論模型及計算方法

1.1 運動方程

參照文獻［1，3，6］，本文采用平均模型理論:將昆蟲看作一個6自由度的剛體，并利用拍動周期內的平均氣動力和氣動力矩來代替翅膀的拍動作用，從而昆蟲的運動方程可簡化為類似于傳統飛機的運動方程.

為方便描述昆蟲的運動，引入固聯于地面的慣性系Oexeyeze和右手體軸系Oxyz(見圖1).體軸系原點O位于昆蟲的質心;平衡飛行狀態下，x軸和y軸分布在水平面內，x軸指向前方，y軸指向身體的右側(見圖1).昆蟲運動各狀態變量定義如下:沿3個體軸方向(x，y，z)的速度分量分別為 u，v，w;繞3 個體軸(x，y，z)轉動的角速度分別為p(滾轉角速度)，q(俯仰角速度)和r(偏航角速度);x軸與水平面的夾角為θ(俯仰角)，y軸和水平面的夾角為γ(滾轉角).

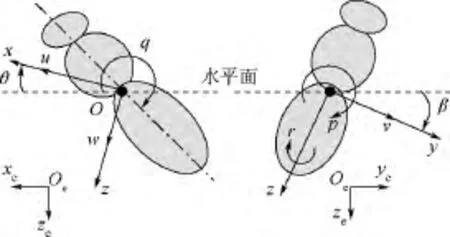
圖1 各狀態變量定義及坐標系示意圖Fig.1 Definition of state variables and sketches of reference frame

昆蟲的總質量記作m;重力加速度記作g;繞x軸、y軸和z軸的轉動慣量分別記作Ix，Iy和Iz，慣性積記作Ixz.X，Y和Z分別為拍動周期內平均氣動力沿x軸、y軸和z軸的分量;L，M和N分別為繞x軸、y軸和z軸的平均氣動力矩.昆蟲的身體運動可近似看作是由穩定的、對稱的平衡狀態量(以下標e表示)和一系列小的擾動分量(以前綴符號δ表示)組成，假設平衡飛行狀態下，ve=we=pe=qe=re=θe=γe=0，前飛速度記作 ue;并且 Xe=Ye=Le=Me=Ne=0，Ze= －mg.在此基礎上對運動方程進行線化，將縱向和橫向運動解耦，對二者分開進行研究(見文獻［13］).線化后的縱向與橫向運動方程如下:

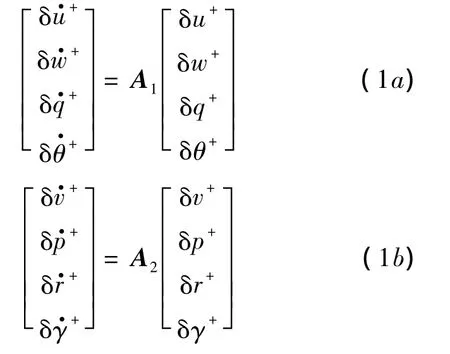
其中A1和A2分別為縱向運動和橫向運動的穩定性矩陣:

其中 Xu，Zu，Mu，Yv，Lv，Nv等為昆蟲運動縱向和橫向穩定性氣動導數.方程(1)和方程(2)中各量均已無量綱化:

其中，St為兩個翅膀的面積;參考速度U為翅膀的平均拍動速度(U=2Φnr2，Φ為拍動幅度，n為拍動頻率，r2為翅膀面積二階矩折合半徑);參考長度c為翅膀平均弦長;參考時間T為拍動周期(T=1/n).

本文采用的蜂蠅模型主要形態學參數如下(蜂蠅運動學和形態學參數均由加州大學伯克利分校Robert Dudley教授提供):身體質量m=145 mg;單個翅膀的質量 mwg=0.326 mg;翅長R=11.2 mm;翅膀平均弦長 c=3.246 mm;翅膀面積二階矩折合半徑r2=0.534R;翅根與翅膀質心間距離 r1，m=0.38R;單個翅膀面積 S=36 mm2;體長lb=1.29R;兩翅根間距離為0.33lb;翅根軸與身體質心間距離l1=0.13lb;自由懸掛時身體的角度 χ0=53.3°;本文采用與文獻［9］中相同的方法估算蜂蠅的轉動慣量和慣性積，懸停和各前飛速度下相應的估計值見表1.至此，縱橫向系統矩陣A1和A2中只差相應的氣動導數未知.

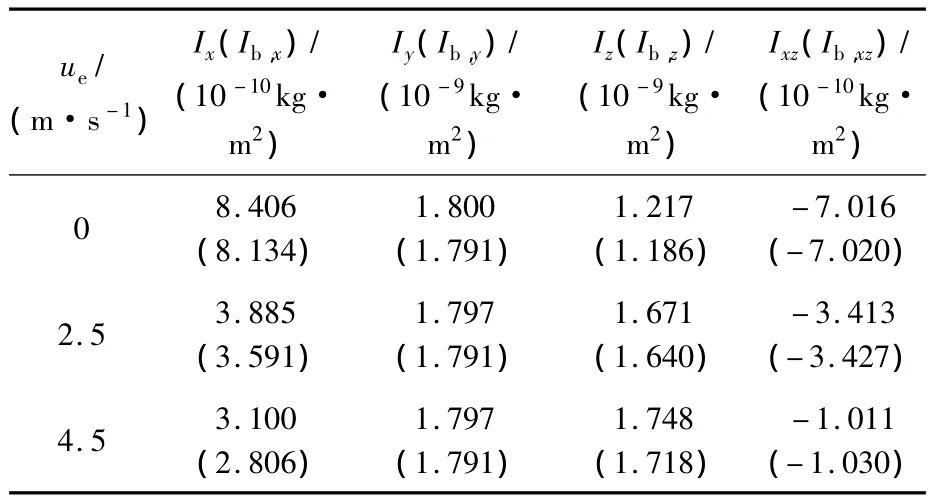
表1 蜂蠅懸停和前飛時相應的轉動慣量和慣性積Table1 Moments and product of inertia of dronefly at hovering and forward flight

1.2 N-S方程求解與氣動導數計算

1.2.1 翅膀和身體的運動

本文所用蜂蠅翅膀平面形狀(如圖2(a)所示)取自文獻［14］，模型翅近似為剛性平板，厚度為平均弦長的3%，前后緣為圓弧.身體模型的外形輪廓如圖2(b)所示.

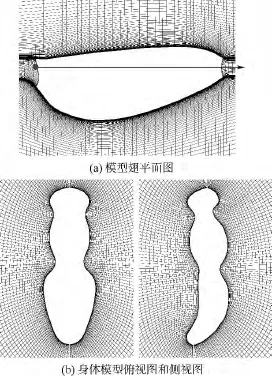
圖2 蜂蠅的翅膀與身體模型Fig.2 Model of a dronefly’s wing and body

懸停和前飛時身體模型的速度(飛行速度ue)和姿態(身體角度χ)定義如圖3(a)所示.

為方便描述模型翅的拍動，引入坐標系O1x1y1z1，其坐標原點O1位于翅根，x1y1平面與翅膀拍動平面重合，見圖3(b).模型翅的拍動有兩個自由度:一個為繞O1z1軸的轉動，轉角記為φ，即翅膀的拍動角;另一個為繞翅膀展向軸的轉動，轉角記為α，即是翅膀的攻角.拍動角φ隨時間的變化可近似表示為

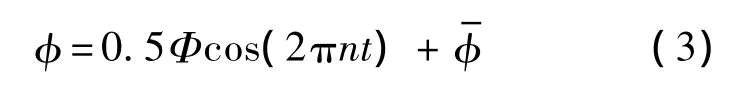
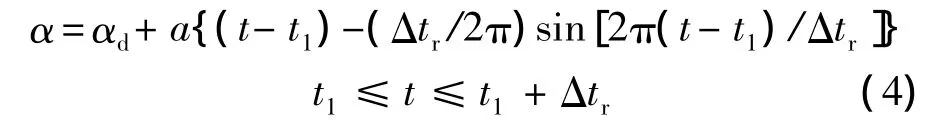
其中，Δtr為翅膀的翻轉時間;a為常數;t1為翅膀開始翻轉的時刻:

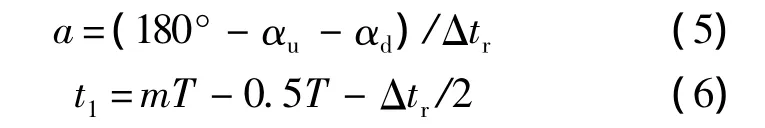
T為翅膀拍動周期.翅膀的下翻運動可用同樣的方式描述.從方程(3)～方程(6)可以看出，為了描述翅膀的拍動，需確定以下參數:Φ，n，Δtr，αd，αu和.為描述拍動平面，還需給出拍動平面傾角β.

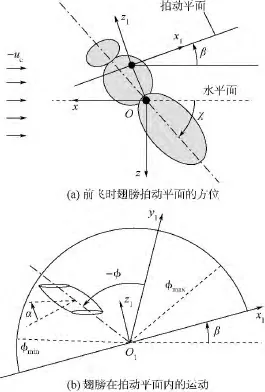
圖3 模型翅運動及坐標示意圖Fig.3 Sketches of reference frames of wing motion

所需運動參數 Ф，n，Δtr，β 和 χ列于表2，Δtr在懸停和前飛下均為0.30T;前進比定義為J=ue/2nΦR.

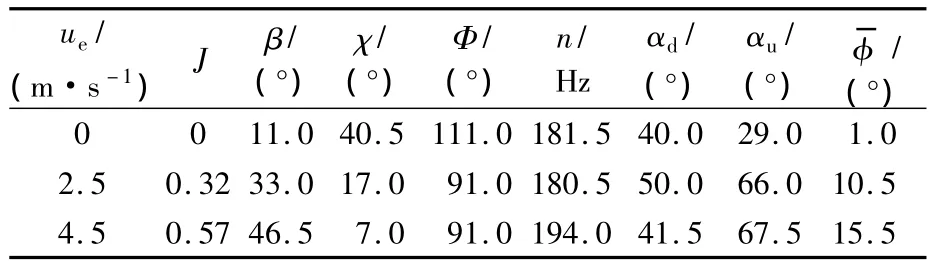
表2 蜂蠅懸停和前飛的運動學參數Table2 Kinematic parameters of dronefly at hovering and forward flight

由于αd和αu的實驗數據存在較大的測量誤差，而且氣動力矩對于的變化也較為敏感，因此，本文通過力和力矩的平衡條件確定αd，αu和:翅膀和身體的平均垂直力之和需平衡昆蟲的體重;翅膀的平均水平力需等于身體的阻力;翅膀和身體對于質心的俯仰力矩之和需等于0.雷諾數Re大小約為948(Re定義:Re=Uc/ν，其中，ν為運動黏度系數，U和c定義如上).

1.2.2 N-S 方程求解

要獲得氣動導數，首先需確定懸停和各前飛速度的平衡狀態.平衡狀態的確定和氣動導數的計算均需數值求解N-S方程.N-S方程數值求解過程在文獻［15-16］中已有較為詳盡的描述，此處不再贅述.本文使用的計算程序已多次在先前的懸停研究中驗證和使用過(例如文獻［9，15］)，前飛計算中只是在遠場邊界加入來流速度，而來流速度等于昆蟲的前飛速度.文獻［17］研究結果顯示左翅和右翅之間的干擾除了在進行“打開和合攏”運動時都可以忽略不計;文獻［18-19］也證實了翅膀和身體間的干擾也較小，可以忽略.因而，繞翅膀和身體的流動可分別進行計算.

計算所用翅膀網格為100×101×107(法向×周向×展向)的O-H型網格，如圖2(a)所示.壁面網格法向間距為0.0015c;遠場邊界約為20c.無量綱時間步長取0.02(以c/U進行無量綱化).基于文獻［16］中對網格密度、時間步長以及算法和程序的驗證，其工作表明，本文使用的數值計算方法是可靠的，各計算參數的選取也是合適的.

身體網格為80×81×95(沿身體模型截面的法向方向×周向方向×身體體軸方向)的O-O型網格，如圖2(b)所示.計算所得身體的升力和阻力與實驗測量結果進行了比較，計算值與實驗測量值的差別基本在昆蟲體重的2%以內，也就是說身體計算模型和真實身體實驗結果間的差別對平衡飛行影響很小.

1.2.3 氣動導數的計算

本文計算氣動導數方法與文獻［6］中縱向穩定性問題的研究方法相同.以縱向氣動導數Xu，Zu和Mu(u-系列)計算為例，即在平衡狀態的基礎上，保持w，q，θ和飛行速度不變(w，q和 θ為0，飛行速度為ue)，調整u可計算得一系列氣動力和力矩(X，Z和M)隨u的變化曲線，曲線在平衡點處的導數就是對應的氣動導數.類似地，還可得到其他縱向氣動導數w-系列和q-系列以及橫向氣動導數v-系列、p-系列和r-系列.

在確定氣動導數的基礎上，本文采用與文獻［6］中縱向動穩定性研究類似的特征值和特征向量方法，方法概述詳見文獻［13］.

2 結果與討論

2.1 懸停和前飛的平衡條件及氣動導數

根據力和力矩的平衡條件，通過求解拍動翅和身體的繞流，確定出蜂蠅懸停和各前飛速度下αd，αu和(見表2).在平衡狀態的基礎上，分別調整縱向狀態變量u，w和q得到相應的氣動力(X+和Z+)和氣動力矩(M+);調整橫向狀態變量v，p和r得到相應的氣動力(Y+)和氣動力矩(L+和 N+).以前飛(J=0.32)為例，縱向和橫向計算結果見圖4(其他飛行狀態結果類似).由圖4可以看出，在 －0.15≤Δu+，Δw+，Δq+≤0.15 范圍內，ΔX+，ΔZ+和 ΔM+相對于 Δu+，Δw+和 Δq+的變化線性較好;由圖5可以看出，在－0.15≤Δv+，Δp+和 Δr+≤0.15 范圍內，ΔY+，ΔL+和 ΔN+相對于Δv+，Δp+和Δr+的變化線性也較好，這意味著對昆蟲運動方程的小擾動線化處理是合理的.

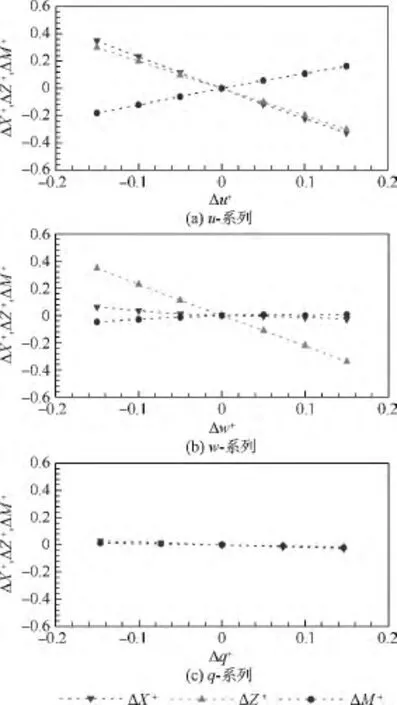
圖4 蜂蠅前飛(J=0.32)時縱向u-系列，w-系列，q-系列無量綱氣動力和力矩Fig.4 The u-series，w-series，q-series non-dimensional force and moment data at J=0.32

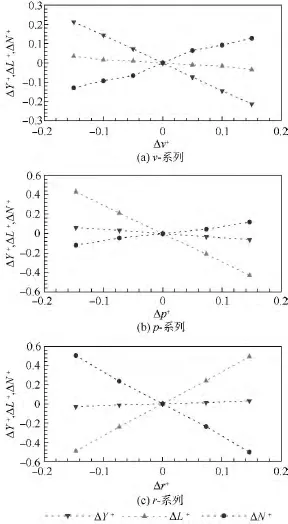
圖5 蜂蠅前飛(J=0.32)時橫向v-系列、p-系列、r-系列無量綱氣動力和力矩Fig.5 The v-series，p-series，r-series non-dimensional force and moment data at J=0.32

根據圖4和圖5計算結果，可分別得到蜂蠅懸停和前飛平衡位置處的縱向和橫向氣動導數，見表3和表4.總的來說，相對于翅膀的氣動導數，蜂蠅身體部分貢獻較小.

首先考慮蜂蠅的縱向運動，由表3可以看出，懸停時(J=0)，Xu+為負，Mu+為正，并且二者的絕對值比Zu+大得多，這表明蜂蠅的前后平移將產生與運動相反的阻力，向前運動時產生抬頭的力矩，反之產生低頭的力矩.Zw+為負且絕對值大于Xw+和Mw+，表明蜂蠅的上下運動將產生與運動方向相反的阻力.蜂蠅的俯仰運動產生的氣動導數(Xq+，Zq+和Mq+)數值均較小.與懸停相比，蜂蠅前飛時的縱向運動除產生了與懸停類似的較大的氣動導數Xu+，Mu+，Zw+外，導數 Zu+的絕對值也增大至與Xu+和Mu+相同的量級.

對蜂蠅的橫向運動而言，由表4可見，懸停時(J=0)，Yv+為負，Lv+為正，而且二者的絕對值比Nv+大得多，這表明昆蟲的側向運動(v+)主要產生一個與運動方向相反的側向力(阻尼力)和一個與運動方向一致的滾轉力矩(稱Yv+為阻尼力導數，Lv+為側滑滾轉力矩導數).Lp+為負且其絕對值比Yp+和Np+大得多，表明昆蟲的滾轉運動(p+)主要產生一個較大的阻尼力矩.類似的，Nr+為負且絕對值較Lr+和Yr+大得多，表明昆蟲的偏航運動(r+)也是主要產生一個阻尼力矩.因此，懸停時昆蟲的橫向擾動運動主要產生一個側滑滾轉力矩(Lv+Δv+)和3個阻尼力和力矩:包括一個側向阻尼力(Yv+Δv+)，一個滾轉阻尼力矩(Lp+Δp+)和一個偏航阻尼力矩(Nr+Δr+).

與懸停相比，蜂蠅前飛時，Lv+的符號發生變化，變為負值;阻尼力和力矩導數(Yv+，Lp+和Nr+)絕對值進一步增大;偏航滾轉力矩導數(Lr+)變化也較為顯著，達到與阻尼力矩導數(Nr+)同等量級.這意味著，蜂蠅前飛時，其橫向擾動運動產生了一個與運動方向相反的滾轉力矩(Lv+Δv+)，側向阻尼力(Yv+Δv+)、滾轉阻尼力矩(Lp+Δp+)和偏航阻尼力矩(Nr+Δr+)均增大;而偏航運動也可產生一個與阻尼力矩(Nr+Δr+)相當的滾轉力矩.

2.2 特征模態和穩定特性

計算得到氣動導數之后，方程(2)中系統矩陣A1和A2中各元素均可確定.應用特征模態的分析方法求解方程(2)可進一步分析蜂蠅的縱向和橫向動穩定性.應用MATLAB軟件分別計算系統矩陣A1和A2可得相應的特征值和特征向量.A1和A2的特征值計算結果分別見表5和表6.

表3 縱向氣動導數Table3 Longitudinal aerodynamic derivatives

表4 橫向氣動導數Table4 Lateral aerodynamic derivatives

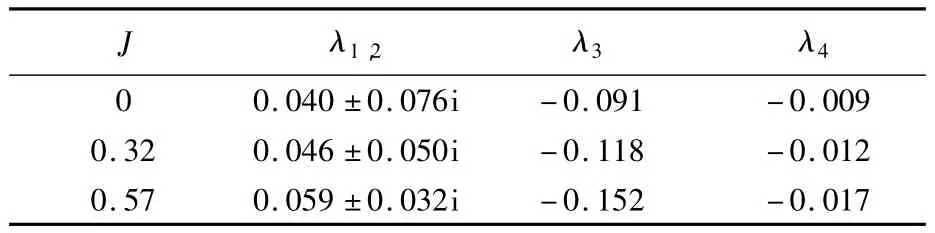
表5 蜂蠅懸停和前飛時縱向穩定性矩陣特征值Table5 Eigenvalues of longitudinal system matrix of dronefly at hovering and forward flight

表6 蜂蠅懸停和前飛時橫向穩定性矩陣特征值Table6 Eigenvalues of lateral system matrix of dronefly at hovering and forward flight

蜂蠅的懸停和前飛縱向運動均存在一對實部為正的復數特征值 λ1，2和兩個負的實特征值 λ3和λ4，這意味著蜂蠅的縱向運動由不穩定振蕩模態、快衰減模態和慢衰減模態3個特征模態構成.懸停的結果與文獻［3，6］對若干種昆蟲的縱向穩定性研究類似.

本文所考慮的2種前飛速度的縱向特征模態結構上與懸停相同;表面上來看，這與熊蜂前飛［7］時的結果有所不同(熊蜂懸停和低速前飛時由不穩定振蕩模態、快衰減模態和慢衰減模態構成;中等速度前飛時由2個振蕩模態組成;較高的前飛速度由4個單調模態組成).但是，由表5可以看出，隨著飛行速度的增大，蜂蠅縱向穩定性矩陣的復數特征值的實部在逐漸增大，意味著其不穩定性在逐漸增強，這種發展的趨勢是與熊蜂的前飛縱向穩定性研究結果［7］一致的.與熊蜂最大前飛速度相比，蜂蠅高速前飛(J=0.57)時未出現4個實特征值的原因主要在于氣動導數M+w較小.將前飛(J=0.57)時 M+w人為增大約1倍(M+w=0.60)，系統矩陣A1中其他變量不變，可得特征值:λ1=0.132，λ2= － 0.196，λ3= －0.015，λ4=0.027;這種特征值的結構與熊蜂最大前飛速度的結果類似［7］.在較大的前飛速度下，Mw+對熊蜂的縱向穩定性有著重要作用，且身體部分對其貢獻占主要部分［7］;而蜂蠅前飛時，身體部分對氣動導數的貢獻相對熊蜂要小，這可能是由于兩種昆蟲身體的外形差異引起的.

對于橫向運動而言，懸停(J=0)時，存在一個正的實特征值λ1，一對實部為負的復數特征值λ2，3和一個負的實特征值λ4.它們分別代表了不穩定發散模態、穩定振蕩衰減模態和穩定的衰減模態.這與文獻［9，12］中懸停的橫向穩定性結果一致.

前飛時蜂蠅橫向運動系統矩陣的特征值結構與懸停(J=0)類似，但是特征值λ1隨著飛行速度的增大而明顯減小(前飛J=0.57時λ1=0);相應地，其橫向運動的不穩定性在逐漸減弱;尤其是大前飛速度下(J=0.57)，λ1=0，可視其為一種中性的穩定.蜂蠅前飛時這種橫向運動的穩定性變化趨勢與文獻［12］中熊蜂前飛的研究結果也是一致的.

特征模態中，振蕩模態的周期T和擾動增長倍幅期tdouble或擾動衰減的半衰期thalf可以更為直觀地顯示蜂蠅穩定性變化的趨勢，相應的計算公式［13］如下:

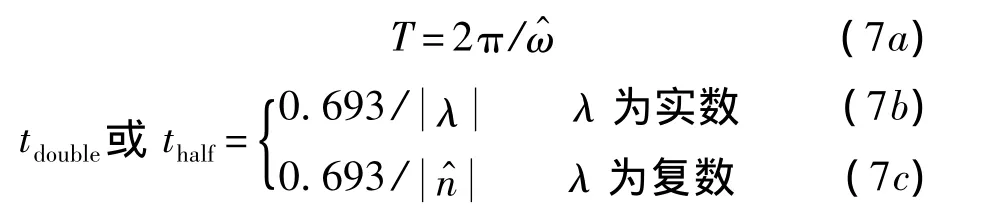
表7 縱向特征模態的時間常數Table7 Time constant of longitudinal natural modes

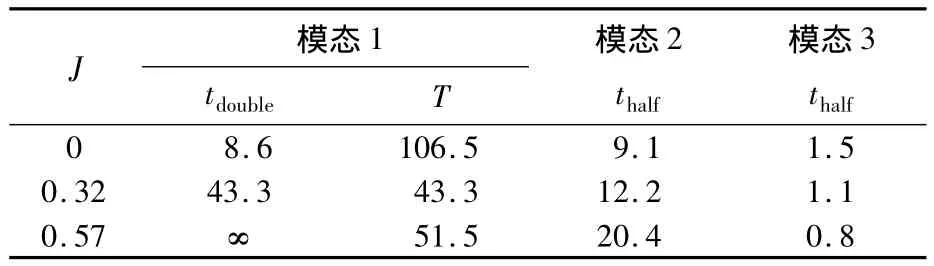
表8 橫向特征模態的時間常數Table8 Time constant of lateral natural modes

由表7可見，懸停時縱向運動的不穩定發散模態倍幅期tdouble≈17.3T，即初始擾動將在約17個拍動周期后幅值加倍;隨著前飛速度的增大，不穩定發散模態的倍幅期tdouble在逐漸減小，也就是說初始擾動幅值加倍所需的時間在逐漸縮短，縱向運動的不穩定性即在逐漸地增強.

由表8可以看出，蜂蠅懸停時橫向不穩定發散模態的倍幅期tdouble≈8.6T，而前飛時相應的倍幅期在逐漸增大(J=0.32時約為43T，J=0.57時趨于無窮大)，即前飛時橫向擾動的發散增長需要相對較長的時間，這也更直觀地說明了蜂蠅前飛時橫向的不穩定性在逐漸減弱;基于較長的倍幅期數值，可以將蜂蠅前飛的橫向運動看作較弱或中性穩定.

運動各模態對應的特征向量決定了模態對應各狀態變量的相位關系和幅值的相對大小.表9和表10分別給出了縱向和橫向各特征模態對應特征向量的極坐標形式;由于特征向量的模可以為任意大小，而方向是唯一確定的，因此縱向和橫向的結果分別用角度量δθ和δλ將特征向量歸一化.

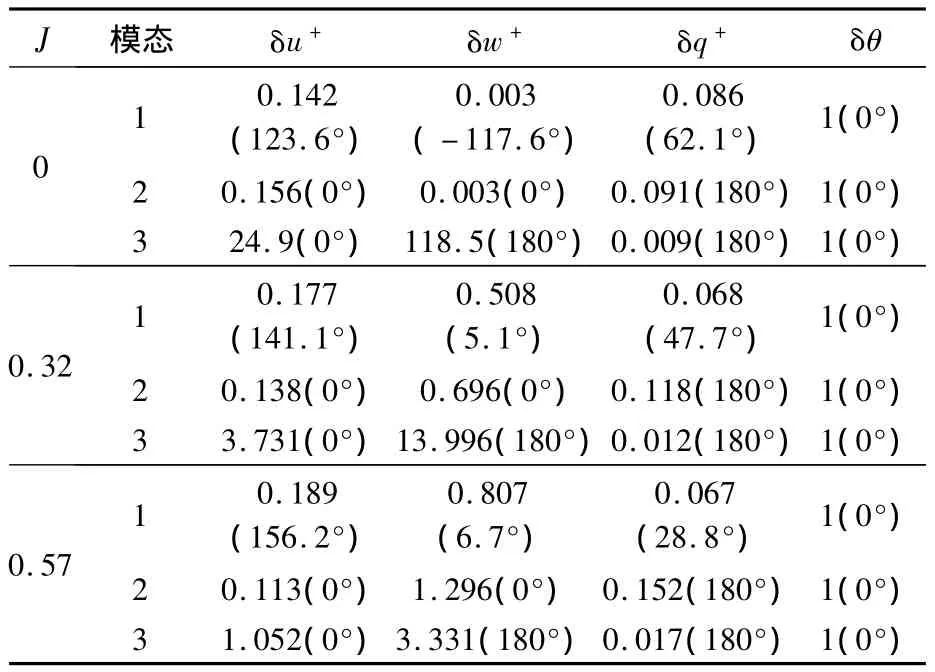
表9 蜂蠅懸停和前飛時縱向各模態對應的特征向量Table9 Eigenvectors of longitudinal natural modes of dronefly at hovering and forward flight

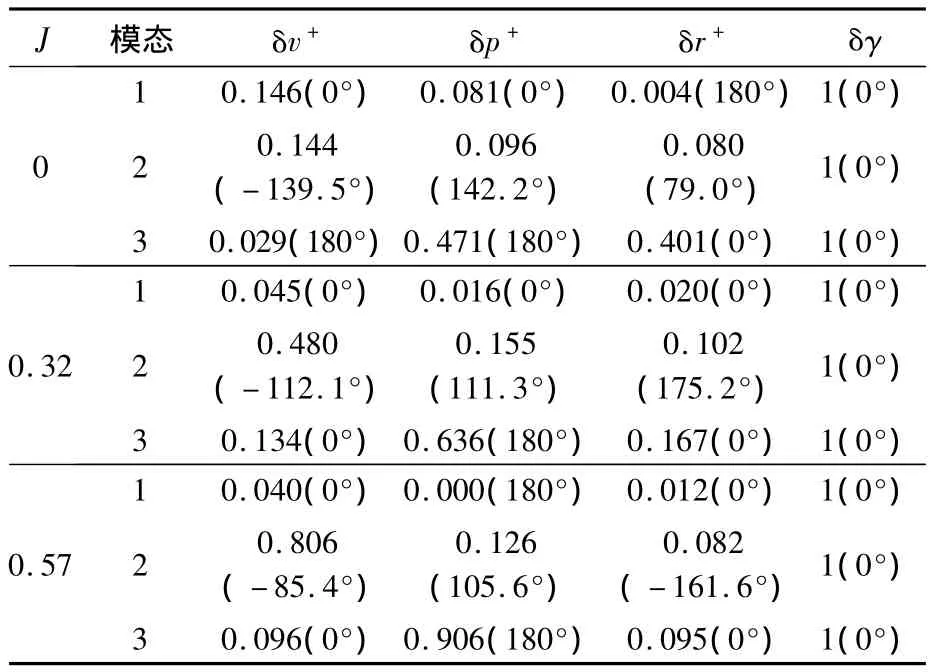
表10 蜂蠅懸停和前飛時橫向各模態對應的特征向量Table10 Eigenvectors of lateral natural modes of dronefly at hovering and forward flight

由表9和表10可分別看出縱向和橫向各特征模態所對應的運動，具體闡釋見早前懸停和前飛的研究工作［3，7，9］.

3 結論

1)蜂蠅懸停時縱向擾動運動由不穩定振蕩模態、快衰減模態和慢衰減模態構成;橫向擾動運動由不穩定發散模態、穩定振蕩衰減模態和穩定的衰減模態構成.蜂蠅縱橫向運動中均有不穩定模態存在，表明其懸停是不穩定的.

2)蜂蠅前飛時的縱向擾動特征模態結構與懸停時相同，但其不穩定發散模態的倍幅期tdouble隨著前飛速度的增加逐漸減小，這意味著初始擾動幅值加倍的時間在逐漸縮短，即蜂蠅前飛時縱向不穩定性在逐漸增強，對飛行不利.

3)蜂蠅前飛時的橫向運動由于氣動導數L+v的變化(由正變負)，代表其不穩定模態的特征值逐漸減小至零，不穩定發散模態的倍幅期不斷增大，這意味著前飛時蜂蠅的橫向不穩定性較懸停不斷減弱，趨于一種中性的穩定.

4)盡管蜂蠅前飛時橫向的不穩定在逐漸減弱，但其飛行穩定性包括縱向和橫向兩方面，而前飛時縱向的不穩定性在逐漸增強，因此，總體上來說，蜂蠅的前飛也是不穩定的.

References)

［1］ Taylor G K，Thomas A L R.Dynamic flight stability in the desert locust Schistocerca gregaria［J］.Journal of Experimental Biology，2003，206(16):2803-2829.

［2］ Schenato L，Wu W C，Sastry S.Attitude control for a micromechanical flying insect via sensor output feedback［J］.IEEE Transactions on Robotics and Automation，2004，20(1):93-106.

［3］ Sun M，Xiong Y.Dynamic flight stability of a hovering bumblebee［J］.Journal of Experimental Biology，2005，208:447-459.

［4］ Deng X，Schenato L，Wu W C，et al.Flapping flight for biomimetic robotic insects，part I:system modeling［J］.IEEE Transactions on Robotics，2006，22(4):776-788.

［5］ Liu H，Nakata T，Gao N，et al.Micro air vehicle-motivated computational biomechanics in bio-flights:aerodynamics，flight dynamics and maneuvering stability［J］.Acta Mechanica Sinica，2010，26(6):863-879.

［6］ Sun M，Wang J K，Xiong Y.Dynamic flight stability of hovering insects［J］.Acta Mechanica Sinica，2007，23(3):231-246.

［7］ Xiong Y，Sun M.Dynamic flight stability of a bumblebee in forward flight［J］.Acta Mechanica Sinica，2008，24(1):25-36.

［8］ Faruque I，Humbert J S.Dipteran insect flight dynamics，part 1:longitudinal motion about hover［J］.Journal of Theoretical Biology，2010，264(2):538-552.

［9］ Zhang Y L，Sun M.Dynamic flight stability of a hovering model insect:lateral motion［J］.Acta Mechanica Sinica，2010，26(2):175-190.

［10］ Faruque I，Humbert J S.Dipteran insect flight dynamics，part 2:lateral-directional motion about hover［J］.Journal of Theoretical Biology，2010，265(3):306-313.

［11］ Cheng B，Deng X Y.Translational and rotational damping of flapping flight and its dynamics and stability at hovering［J］.IEEE Transactions on Robotics，2011，27(5):849-864.

［12］ Xu N，Sun M.Lateral dynamic flight stability of a model bumblebee in hovering and forward flight［J］.Journal of Theoretical Biology，2013，319:102-115.

［13］ Etkin B，Reid L D.Dynamics of flight:stability and control［M］.New York:Wiley，1996.

［14］ Ellington C P.The aerodynamics of hovering insect flight.II.morphological parameters［J］.Philosophical Transactions of the Royal Society of London，Series B:Biological Sciences，1984，305(1122):17-40.

［15］ Sun M，Tang J.Unsteady aerodynamic force generation by a model fruit fly wing in flapping motion［J］.Journal of Experimental Biology，2002，205(1):55-70.

［16］ Wu J H，Sun M.Unsteady aerodynamic forces of a flapping wing［J］.Journal of Experimental Biology，2004，207(7):1137-1150.

［17］ Sun M，Yu X.Aerodynamic force generation in hovering flight in a tiny insect［J］.AIAA Journal，2006，44(7):1532-1540.

［18］ Yu X，Sun M.A computational study of the wing-wing and wing-body interactions of a model insect［J］.Acta Mechanica Sinica，2009，25(4):421-431.

［19］ Liang B，Sun M.Aerodynamic interactions between contralateral wings and between wings and body of a model insect at hovering and small speed motions［J］.Chinese Journal of Aeronautics，2011，24(4):396-409.