基于泊松理論的動態股票網絡投資模型

李 艷，韓 華，汪金水

（武漢理工大學理學院，武漢430070）

0 引言

近年來，對復雜網絡的研究越來越受到學者們的關注，復雜網絡對于研究復雜系統的聚類及演化規律具有重要作用。股票網絡作為復雜網絡中的一種，是以股票及其投資者為網絡中的節點，股票與投資者之間的投資關系為連邊的復雜系統，股票網絡中以節點和連邊來構建股票網絡方法的研究也不唯一，Mantegna［1］利用最小生成樹的方法來構建網絡，通過找到股票之間重要的連接揭示網絡的層次結構；R.Gu等［2］以股票為網絡的節點，通過邊相關系數閾值方法構建無權無向的股票網絡；萬陽松等［3］則將股票的相關系數cij作為網絡的股票之間的權重來構建無向含權股票網絡；馬源源等［4］以上市公司及其主要股東為節點，以其持股關系為連邊，持有股票份額為權重建立了有向含權的股票投資網絡，這些研究都是在給定時間序列的基礎上進行研究的，是對靜態網絡的研究。

目前，對動態股票網絡進行的研究比較少，陳俊華等［5］在確定研究日期以后，每隔N個時間間隔構建一個股票網絡，從而得到一系列連續動態網絡，進而研究股票市場的動態變化規律，然而，在現實網絡中，尤其是在股票網絡中，時間序列經常是不斷變化并且時間間隔是不均勻的［6－7］

近來，不少學者通過隨機過程理論來描述動態復雜網絡的產生過程。郭進利［8］以供應鏈網絡為研究對象，提出了節點的到達過程服從更新過程，研究了網絡中節點的平均度分布，得出了網絡的穩態平均度分布具有雙向冪律性；楊琴等［9］在供應鏈網絡模型的基礎上提出以泊松過程來描述節點的增加，節點的入邊與出邊服從二項分布，網絡中節點間連邊服從擇優連接，股票間邊的權重服從動態演化，最后得出網絡的穩態平均入強度和穩態平均出強度服從冪律分布。

泊松過程是一個計數過程，它描述的是我們所觀察事件的出現次數，本文中通過泊松過程來描述股票網絡投資的發生，顯然，通過泊松過程來描述復雜網絡中新節點的加入比將節點描述為等時間間隔加入更接近實際情況。泊松過程描述的是一個具有參數λ的新節點到達系統的情況，即新節點到達系統的頻率是固定不變的，然而投資者進行股票投資或者新的股票進入投資系統往往受當時社會的政治、經濟，以及整個股票投資系統的環境的影響，投資者或股票加入系統的頻率并不是固定不變的。如果將股票投資系統內所有不同時間段的投資情況看作是一個總體，其中不同時間段的投資情況由于投資環境的影響存在差異，可以把這種差異解釋為給定λ時，投資者到來數量的條件分布。

基于此，本文提出通過條件泊松過程描述網絡中新節點的到達、投資者對所投資股票的選擇服從擇優選擇、系統內權重符合動態演化規律的動態股票投資網絡。

1 定義

假設將所有股票及其投資者作為股票投資網絡中的節點，系統內的權重為投資者對股票的投資額，系統內邊的方向為節點之間的投資關系，例如，有向邊〈i，j〉代表節點i將自己的資金用于節點j的投資，即節點j吸收了節點i的投資，則系統內的節點都既可以是投資者也可以是被投資者，節點之間也可以互相投資，即網絡中投資者和被投資者兩類節點的性質相同。且系統內的邊既可以是單向邊，也可以是雙向邊，即該股票投資系統是一個有向含權網絡，節點的強度指標反映的是節點在股票網絡中的重要程度，強度越大的節點在股票網絡中越重要。我們研究的股票網絡是一個有向網絡，可以將節點的強度分為入強度SIi和出強度SOi。本文研究的股票網絡中節點的數目以及邊的權重都是動態變化的，并且通過擇優連接機制來描述進入系統的投資者對所投資的股票的選擇情況。

定義1 節點的入強度SIi是股票i吸收的所有投資額，即

定義2 節點的出強度SOi為投資者i進入系統后的所有投資額，即

定義 3［9］令如 果 極 限，則稱極限為網絡穩態平均入強度分布，記為P｛SI＝s｝。

定義 4［9］令如 果 極 限則稱極限為網絡穩態平均出強度分布，記為P｛SO＝s｝。

2 模型描述

2.1 新節點的到來

假設所研究的時間間隔為t，可以將其分割成一個彼此互不相交的時間序列，設系統在時間ti內增加節點的發生頻率為λi，用隨機變量Λ代表系統內新增加節點的頻率，則概率P（Λ＝λi）＞0。設Λ的分布是G，那么隨機選擇一個長度為t的時間區間內到達系統的新節點數量為n的概率［10－11］為

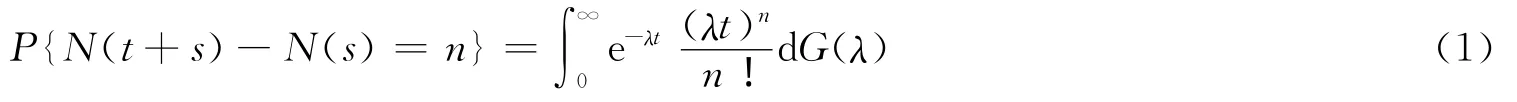
假設網絡中原有的節點數為m0，每個新節點可以對網絡中不同的節點投資，或者接受網絡中其他節點的投資，即每個新節點進入系統后有m條有向邊連接到網絡中已經存在的m個不同的節點（m≤m0），其中新節點的入邊數服從二項分布B（m，p），出邊數服從二項分布B（m，1－p），p∈ （0，1），新邊的初始權重為ω0［9］。

2.2 投資者進入投資系統后對所投資股票的選擇

一般來說，投資者進入系統后，較容易選擇那些有較多投資者投資、吸收較多投資額的股票來進行投資，即節點之間的連邊服從擇優連接，投資者j進入系統后選擇對股票i進行投資的概率依賴于股票i的入強度和投資者j的出強度：

2.3 網絡中權重的變化

實際上，隨著時間的推移，股票系統中的總投資額并不會無限制增加，當時間無限增大，總投資額便會趨于一個常量，為了表示這種變化，引入一個統計學意義上的常量W［12］，來表示網絡中總的投資額的增長，這里W ＝這個新節點所引起的總的投資額的變化是通過對系統內某些邊的權重的動態演化而實現的，即新節點的增加會影響所建立的股票投資網絡的權重ωij。

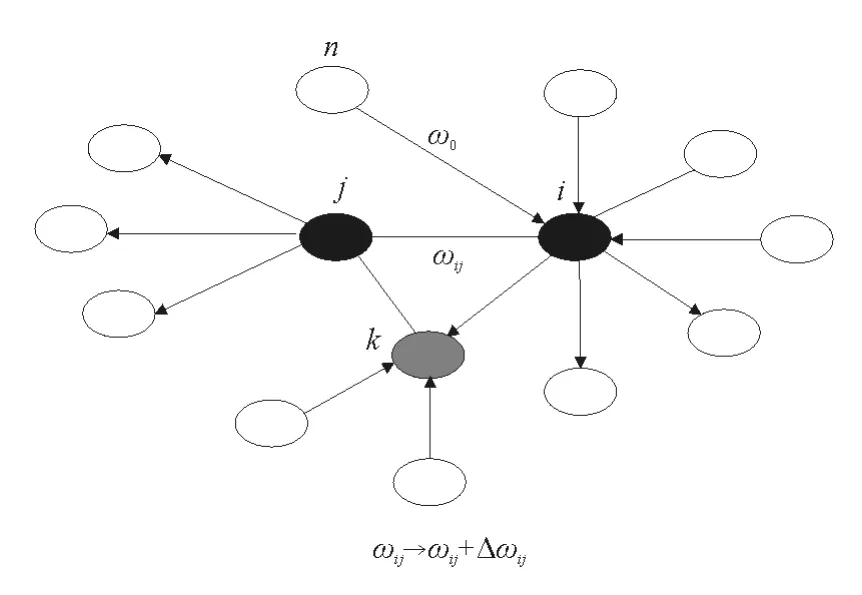
圖1 連邊權重動態演化圖Fig.1 Weight－driven dynamical evolution of linked pairs of vertices

當新節點n加入到網絡中時，它以概率Pni與節點i相連，即新的投資者以Pni的概率將資金用于對i的投資，i可將資金用于自身發展或對節點j和k投資，這就是節點權重的一級耦合機制。當i投資給j后，j可將部分資金用于對k的投資，也就是說i通過j間接對k進行投資，即節點權重的二級耦合機制。本文僅考慮節點權重的一級耦合機制，節點權重的二級耦合機制也可通過類比得到。

因此，用公式（3）來刻畫隨系統中新的投資發生而導致的有向邊的權重的動態演化［12］規律

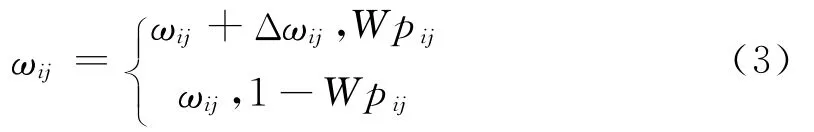
用｛Yi；i≥1｝表示第i個顧客到達系統后進行投資的投資數額，則｛Yi；i≥1｝是獨立同分布的，且｛Nt；t≥0｝與｛Yi；i≥1｝相互獨立，則可以將t時刻進入系統的投資者進行投資的金額總數表示為

3 解析過程

在模型動態演化的過程中，不允許出現自己對自己進行投資的情況，投資者增加對某只股票投資金額的情況只能通過增加該有向邊的權重來表示，而不能出現重復邊。本部分在模型描述所建立股票網絡的基礎上，對其理論可行性進行探討。在分析的過程中，令ω0＝1，且ωij（t），SIi（t），SOi（t）為連續實變量［9］。

3.1 新節點的到達

at為t時刻該股票投資網絡中所有節點的數目，則at＝Nt＋m0≈Nt。由于節點的到達過程符合參數為Λ的條件泊松過程，并且由于任意時刻到達股票投資系統的節點數目是有限的，即E（Λ2）＜∞，由條件泊松過程理論可知，在［0，t］內到達網絡的節點的平均數為tEΛ，即到t時刻平均有tEΛ個節點添加到網絡中，則E［N（t）］＝tEΛ［10－11］。

3.2 新進入系統內投資者的投資數額

｛Xt＝是一個復合條件泊松過程，Xt有獨立增量，且每個投資者的投資數額都是有限的，由泊松理論可知，進入系統的投資者的投資數額總和的均值E［Xt］＝tEΛEY1［10－11］。

3.3 入強度分析

假設ωji（t），SIi（t）為一連續實變量，則可得到權重ωji（t）的變化率為

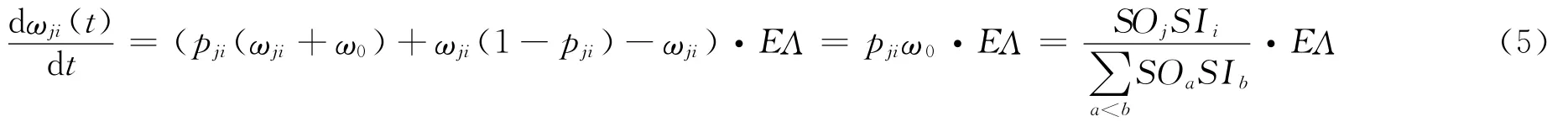
當有新的投資者進入網絡時，會引起股票投資網絡中入強度的變化，對于節點i的入強度SIi（t）來說，它的增加既可以是因為新增加的投資者選擇股票i進行投資而建立起來的新的連接，也可以是因為以節點i為終點的連邊的權重發生變化，因此，節點i的入強度SIi（t）滿足動態方程（6）：

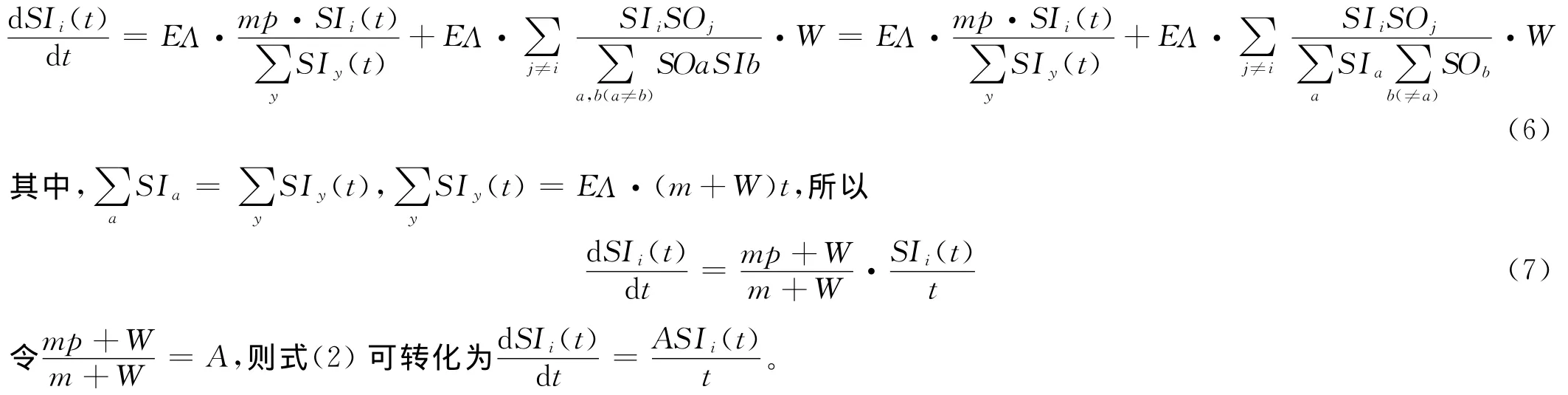
由于新的股票投資者i在ti時刻進入股票投資系統的入強度為SIi（t），則解方程（7）得

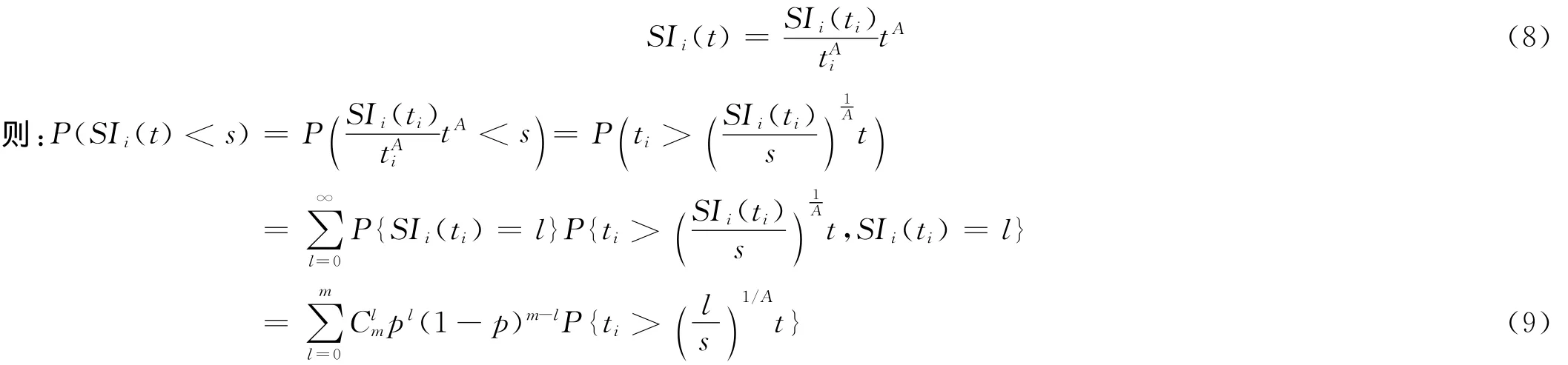
由于復合泊松過程不一定是計數過程，但是當Yi≡c，i＝1，2，…，c為常數時，可化為泊松過程［10－11］。根據前文，令ω0＝1，即Yi≡1，因此可將該復合條件泊松過程化為參數為EΛ的泊松過程。

根據泊松過程理論，第n次事件發生的時刻Tn，n＝1，2，3，…，服從Γ分布，即投資者的到達時間ti服從Γ分布［10－11］，即

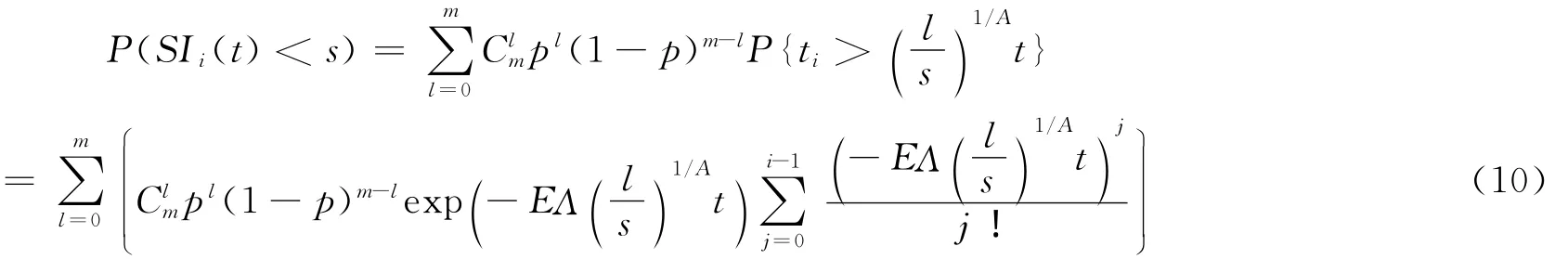
節點i的瞬態入強度分布為

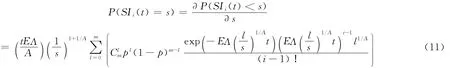
節點i的穩態入強度分布為

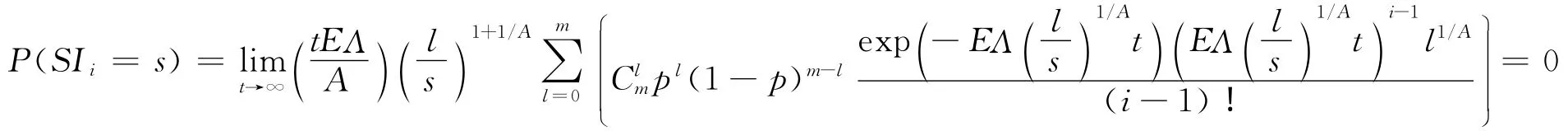
網絡的瞬態平均入強度分布為

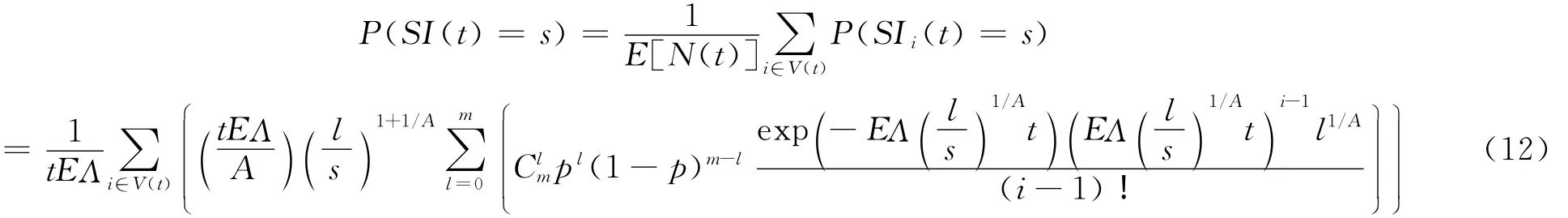
網絡的穩態平均入強度為

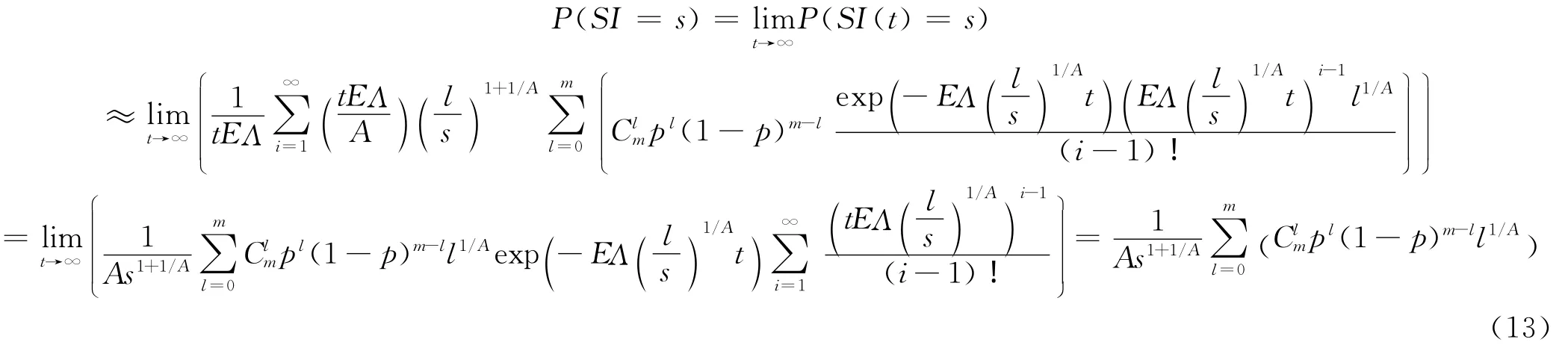
3.4 出強度分析

假設ωij（t）、SOi（t）為一連續實變量，則可得到權重ωij（t）的變化率為

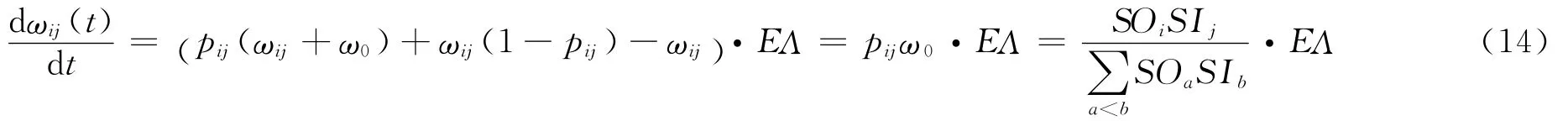
與入強度分析過程類似，對于節點i的出強度SOi（t）來說，它的增加既可以是因為新增加的投資者i選擇股票進行投資而建立起來的新的連接，也可以是因為以節點i為起點的連邊的權重發生變化，因此，節點i的出強度SOi（t）滿足動態方程（15）：

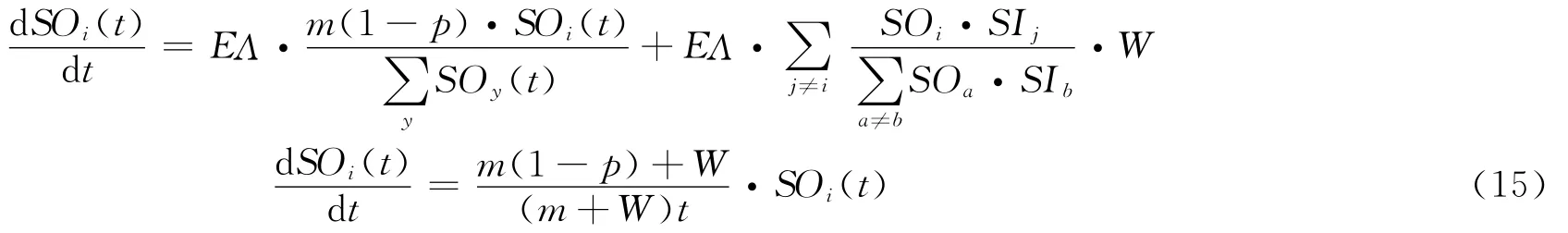
節點i的瞬態出強度分布為

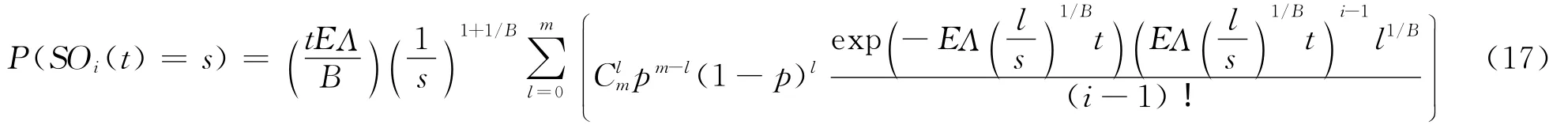
節點i的穩態出強度分布為

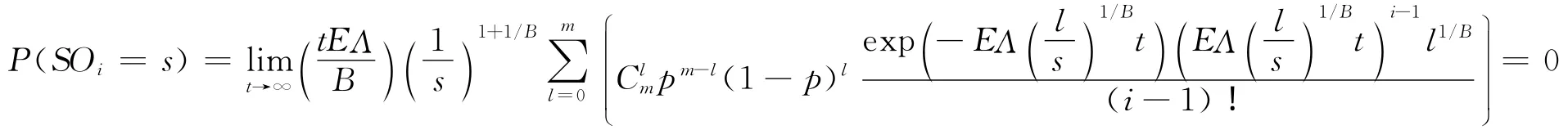
網絡的瞬態平均出強度分布為

網絡的穩態平均出強度分布為

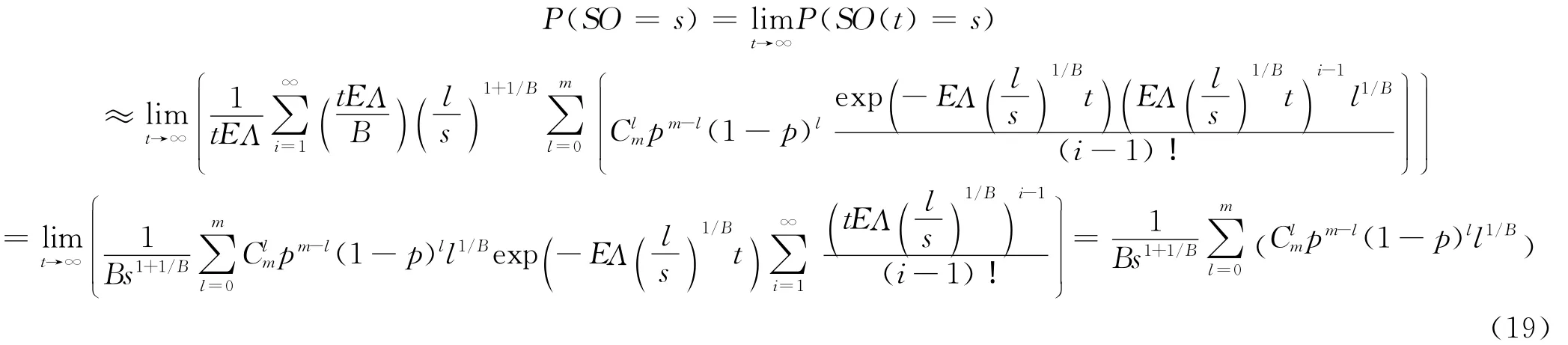
從上述解析過程來看，該網絡的節點穩態入強度分布和穩態出強度分布均為0，網絡的穩態平均入強度分布和穩態出強度滿足冪律分布，即P（SI＝s）～s－γ，冪律指數

4 仿真結果

針對上文模型，通過數值仿真檢驗模型中節點的冪律特性。圖2～圖6分別給出了N＝20 000，λ1＝3，λ2＝4，p1＝0.75，p2＝0.25，N0＝50，W ＝1，m＝1，p3＝0.7時網絡中節點出入強度隨時間演化規律圖以及網絡穩態平均出入強度圖，仿真結果與解析結果比較吻合。

從圖2中，可以看到網絡中節點數目隨時間的變化情況，圖中的點表示在時間t為5 607.982 1時，網絡中的節點數目N為17 992個。

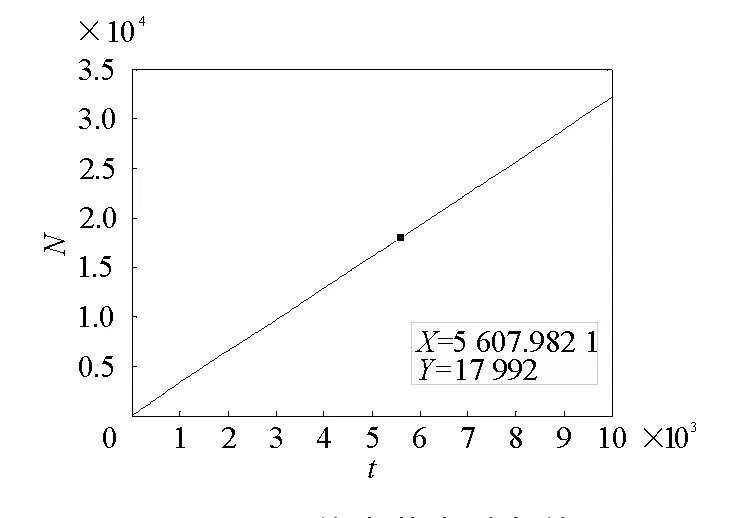
圖2 網絡中節點以條件泊松機制加入過程圖Fig.2 New nodes join in with the mechanism of doubly stochastic Poisson process

圖3 網絡中節點入強度隨時間演化規律圖Fig.3 Evolution rule of the node’s in－strength

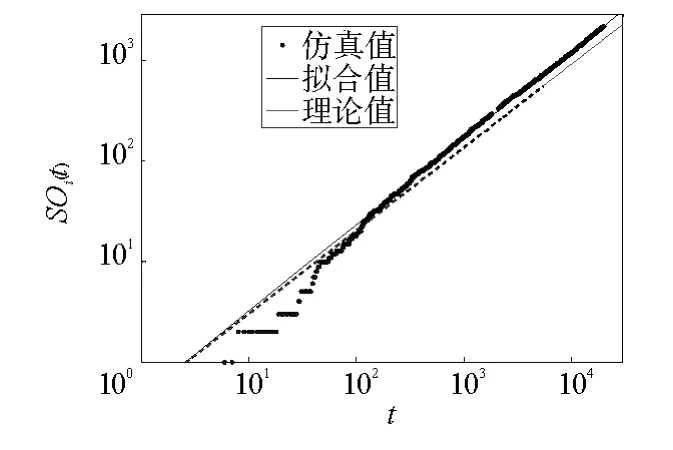
圖4 網絡中節點出強度隨時間演化規律圖Fig.4 Evolution rule of the node’s out－strength

圖3和圖4分別給出了t1＝1.95和t2＝4.26時加入網絡中的兩節點的出入強度隨時間的演化規律圖。節點出入強度的擬合值分別為0.84和0.63，與方程（3）、（11）的解析結果值0.85和0.65比較吻合。

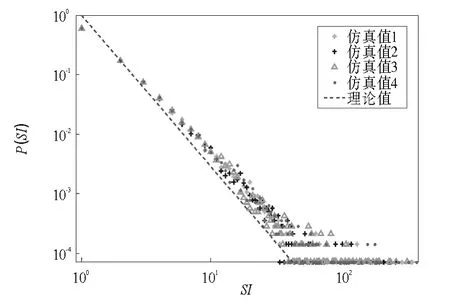
圖5 網絡穩態平均入強度分布圖Fig.5 Average steady in－strength of the network

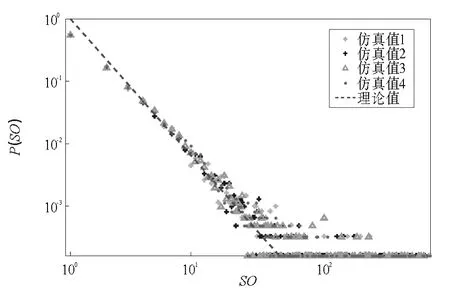
圖6 網絡穩態平均出強度分布圖Fig.6 Average steady out－strength of the network

在圖5和圖6中通過相同參數的4次仿真結果分別給出了網絡穩態平均出入強度的仿真值和解析估計值。網絡穩態平均入強度的4次仿真的理論值均為0.65，仿真值分別為0.62，0.63，0.66，0.64；網絡穩態平均出強度的4次仿真的理論值均為0.86，仿真值分別為0.85，0.84，0.83，0.85。從4次仿真結果可以看出，該股票投資網絡演化模型呈現出較明顯的冪律特性，并且仿真結果與解析估計值也比較吻合。

5 結論

本文通過條件泊松過程加入新節點來建立股票投資網絡的動態模型，該模型同時考慮了方向、權重、擇優連接機制和權重的動態演化，能更真實地反映出投資網絡模型實際的動態變化過程，解析及仿真結果表明，該網絡穩態出入強度服從冪律分布。模型在考慮動態演化時僅考慮了節點數目的增長，并沒有考慮老節點的退出以及網絡中既存節點之間的互連情況，在今后的工作中可以從這幾方面來對模型進行改進，使其能夠更好地描述現實世界中的股票投資網絡。

［1］ Mantegna R.Hierarchical structure in financial markets［J］.European Physical Journal B，1999，11（1）：193－197.

［2］ Gu R ，Shao Y ，Wang Q .Is the efficiency of stock market correlated with the multifractality？an evidence from Shanghai stock market［J］.Physica A，2012，392（2）：361－370.

［3］ 萬陽松，陳忠.加權股票網絡中的無標度行為研究［C］／／第二屆全國復雜動態網絡學術論壇，北京，2005：21－27.Wan Songyang，Chen Zhong.Scale－free behavior in a novel weighted stock network［C］／／The Second National Forum on Complex Dynamic Networks，Beijing，2005：21－27.

［4］ 馬源源，莊心田，李凌軒.滬深兩市股權關聯網絡的社團結構及其穩健性［J］.系統工程理論與實踐，2011，12（1）：2241－2251.Ma Yuanyuan，Zhuang Xintian，Li Lingxuan.Community and robustness of the correlated networks of stock ownership structure［J］.Systems Engineering－Theory and Practice，2011，12（1）：2241－2251.

［5］ 陳俊華.中國股票市場網絡模型動態研究［D］.浙江：浙江工業大學理學院，2012.Chen Junhua.Dynamic study on network models of Chinese stock market［D］.Zhejiang：Zhejiang University of Technolgy，2012.

［6］ He L Y，Chen S P.Multifractal detrended cross－correlation analysis of agricultural futures markets［J］.Chaos，Solitons ＆Fractals，2011，44（6）：355－361.

［7］ Wang G J，Xie C，Han F，et al.Similarity measure and topology evolution of foreign exchange markets using dynamic time warqing method：evidence from minimal spanning tree［J］.Physic A，2012，391（1）：4136－4146.

［8］ 郭進利.供應鏈型網絡中雙冪律分布模型［J］.物理學報，2006，55（8）：3916－3921.Guo Jinli.The bilateral power－law distribution model of supply chain networks［J］.Acta Physica Sinica，2006，55（8）：3916－3921.

［9］ 楊琴，陳云.基于泊松過程的供應鏈復雜網絡模型［J］.系統工程，2012，30（9）：57－62.Yang Qin，Chen Yun.Supply chain complex network model based on poisson process［J］.Systems Engineering，2012，30（9）：57－62.

［10］Ross S M.Stochastic processes［M］.New York：John Wiley ＆Sons Inc，1983：36－44.

［11］孫洪祥.隨機過程［M］.北京：機械工業出版社，2007：136－146.

［12］Wang W X，Wang B H.General dynamics of topology and traffic on weighted technological networks［J］.Phys PRL，2005，94（18）：188702.