反饋強度對非線性光電延遲反饋環動力學的影響

王玉春，李曉文

（北京師范大學物理系，北京100875）

0 引言

1979年，Ikeda在研究非線性光學諧振腔時，從Maxwell－Debye方程中推導出了延遲偏微分方程（DDE），他對此方程進行數值分析后發現：隨著系統控制參數的改變，系統會有周期態和混沌態的輸出［1］。混沌態是自然界中普遍存在的一種現象，其基本特性就是對初值條件極為敏感，具有隨機變化的特點，它的動力學行為具有長期不可預測性，因此，在保密通信、傳感器網絡、超寬帶混沌雷達等領域有著重要應用。為此，很多人致力于能找到一個可以用DDE方程來描述其動力學性質的實驗系統，并將此類系統作為信號發生器應用于實踐中。

近幾十年來，人們不斷調整實驗裝置，從純光學系統到光電系統的改進，不僅增加了系統操作的穩定性，也增加了系統動力學的復雜性。我們所研究的非線性光電反饋延遲系統就是經過多次改進的實驗系統［2］（見圖1）。此類系統主要由半導體激光器、馬赫－曾德爾（M－Z）光強調制器、光電探測器、交流耦合放大器等元件組成光電反饋環。M－Z光強調制器透射的光強與加在調制器上的調制電壓成余弦平方關系，這是此系統非線性的來源。

非線性光電延遲反饋環在非線性、延遲和反饋的共同作用下會呈現出豐富的動力學狀態［3］，包括各種周期態、混沌態。近年來，在現代科技發展的進程中，實驗、數學分析及計算機數值模擬等多種研究手段的共同運用使得我們可以更清晰地研究復雜系統的動力學。人們對非線性光電延遲反饋環的研究主要集中于兩方面：系統在控制參數改變時所呈現的動力學狀態；能夠產生用于實際應用的混沌態。本文主要對其動力學狀態進行理論分析和數值模擬。

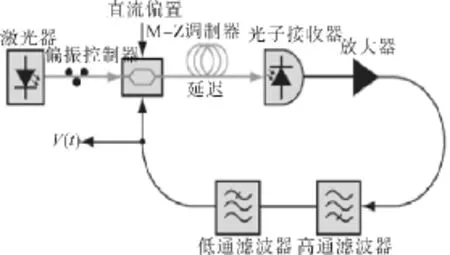
圖1 非線性光電反饋延遲系統Fig.1 Time－delayed feedback nonlinear optoelectronic system

1 非線性光電延遲反饋環的數學模型

用式（1）的DDE方程［4］來描述非線性光電延遲反饋環的動力學性質：

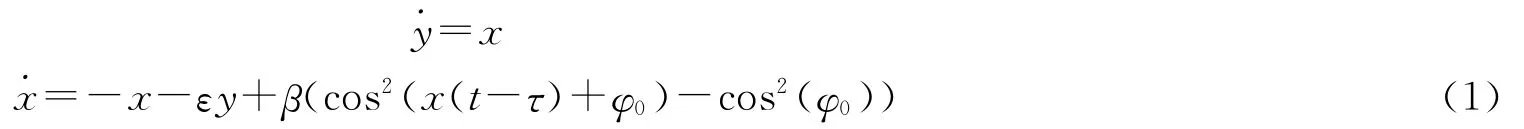
其中，β為反饋強度，ε為低通濾波器與高通濾波器時間常數的比值，τ為時間延遲，φ0為M－Z光強調制器的偏置相位。本文取ε＝2.45×10－6，φ0＝π／4，τ＝34.3ns。

對不動點的穩定性進行分析，將方程進行變分可得

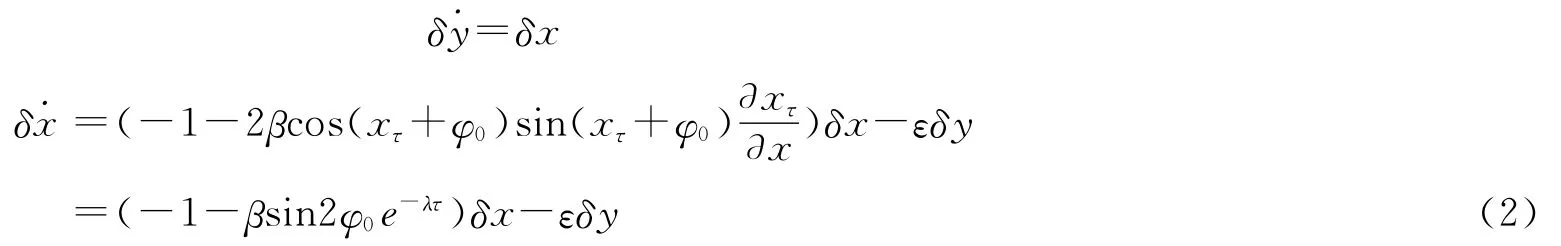
其中，xτ＝x（t－τ），λ為方程的特征值。對應的特征值方程為

整理可得

當特征值λ的值為純虛數時，也就是說當λ＝±iω時，會出現Hopf分岔。取γ＝βsin2φ0，方程（4）轉化為

2 不同反饋強度下系統呈現的各種動力學狀態

我們所研究的非線性光電延遲反饋環的動力學方程解的情況比較復雜，精確解的計算比較困難。我們主要通過數值模擬對系統的動力學狀態進行研究。該系統的控制參數主要有兩個：反饋強度β和偏置相位φ。本文主要研究系統的動力學狀態隨反饋強度的改變而發生的變化。從圖3中可以看出，隨著反饋強度β的增加，系統由穩態經過一系列周期態最終到達混沌態，經歷了從簡單到復雜的一系列豐富的動力學狀態：當β＜1時，反饋強度低，系統處于穩態；當1＜β＜1.8時，系統處于對應的不同周期態；當β＞1.8時系統的狀態逐漸變得復雜。

圖4給出了系統的反饋強度β比1稍大時系統的狀態，可見，系統處于不同的周期態。當反饋強度的值達到中等強度時，系統的動力學狀態隨著反饋強度的增大變得更為復雜，而且還出現了快慢時間尺度交替的混合狀態，這樣的狀態稱為混沌呼吸子［5］。隨著反饋強度β的增加，系統由原來的低頻周期態發展到二級分岔，系統會出現比較有趣的混合狀態—快尺度的動力學加載到慢尺度的極限環上。圖4b是β＝1.5時的低頻周期態，此時系統的時間尺度為μs，振幅的極值類似于一對不動點，在這個意義上來說，它們附近的動力學較為緩慢。

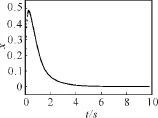
圖2 β＝0.8時系統處在穩定狀態Fig.2 The system is stable whenβ＝0.8

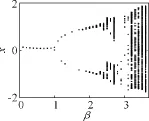
圖3 隨反饋強度的增加系統的分岔圖Fig.3 Bifurcation versus increasing feedback strength

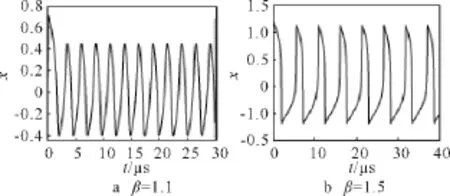
圖4 β＝1.1，β＝1.5時系統處在兩種不同的周期態Fig.4 The system stays at different periodic state asβ＝1.1andβ＝1.5

隨著反饋強度β的進一步增加，β＝1.8時振幅極值點開始出現快尺度的振蕩，如圖5a所示，圖5b是圖5a極值點附近的局部放大圖，可以看出，快尺度的動力學從剛開始產生就經歷了快速的振蕩，而且還是以準方波的周期態出現的。繼續增加反饋強度β的值，β＝2.0時，系統的動力學狀態如圖5c所示，其振幅極值點附近的快尺度動力學狀態所占的時間間隔在增加，從圖5d可以看出，振幅極值點附近的快尺度動力學仍然是以準方波周期態的形式出現的，振蕩一段時間以后很快衰減。

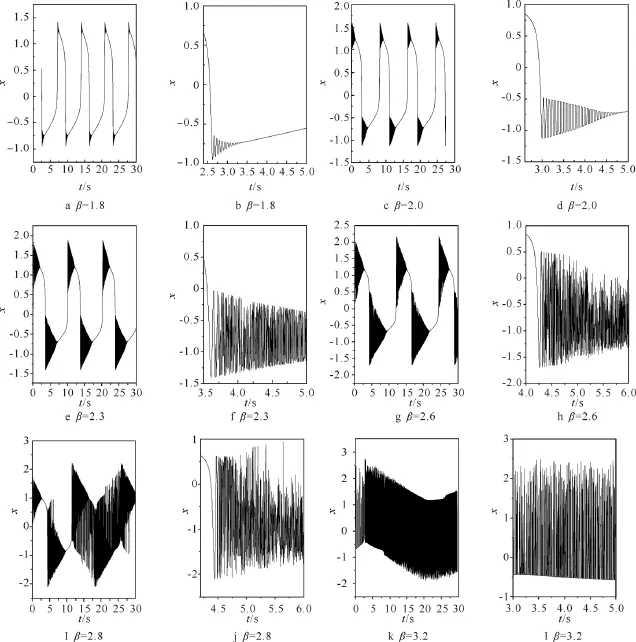
圖5 系統的動力學狀態Fig.5 System dynamic state

當反饋強度β＝2.3時系統還是處于混沌呼吸子狀態，如圖5 e所示。這時從圖5f的局部放大圖中可以看出，振幅極值點附近的快尺度動力學狀態不再是準方波的周期態，從其時間序列看出是一種復雜的混沌態。進一步增加反饋強度β的值，快尺度的動力學狀態所占時間間隔有著明顯的增加，其時間序列更為復雜，時間尺度更快，此時混沌態作為一種快尺度（ns）的動力學狀態被嵌入慢尺度（μs）的周期態中。從上述分析中可以看到，隨著反饋強度β的值越來越大，系統正在向著混沌狀態變化，如圖5g～k所示。圖6為β＝3.2時混沌態的頻譜，從圖中可以看出，其功率譜十分平坦，類似于噪聲。

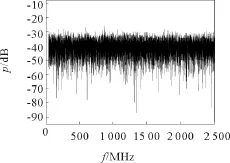
圖6 β＝3.2時系統混沌態的頻譜圖Fig.6 Frequency spectrogram of the chaotic state asβ＝3.2

3 結論

非線性光電反饋延遲系統在非線性、延遲和反饋的共同作用下會呈現出豐富的動力學狀態，包括各種周期態、混沌態。本文首先對于非線性光電反饋延遲系統的數值模型做了理論分析，發現當反饋強度小于1時系統一直處于穩態。反饋強度接近于1時，系統會出現Hopf分岔。得到了系統動力學狀態隨反饋強度變化的分岔圖。隨著反饋強度的增大，系統的動力學狀態從低頻周期態變化到快慢時間尺度混合的混沌呼吸子，最后到達高維混沌態。我們得到了系統的各種動力學狀態的時間序列，并分析了所得混沌態的頻譜圖，發現該系統產生的混沌態的頻譜圖具有噪聲背景和寬峰，這樣的混沌態在很多方面都有重要應用，例如超帶寬傳感器等。

［1］Ikeda K，Kondo K.Successive higher－harmonic bifurcations in systems with delayed feedback［J］.Phy Rev Lett，1982，49：1467－1470.

［2］ Callan K E，Illing L，Zheng Gao，et al.Broadband chaos generated by an optoelectronic oscillator［J］.Phys Rev Lett，2010，104（11）：113901.

［3］ Murphy T E，Cohen A B，Ravoori B.Complex dynamics and synchronization of delayed－feedback nonlinear oscillators［J］.Phil Trans R Soc A，2010，368：343－366.

［4］ Peil M，Jacquot M，Chembo Y K，et al.Routes to chaos and multiple time scale dynamics in broadband bandpass nonlinear delay electro－optic oscillators［J］.Phys Rev E，2009，79（2）：026208.

［5］ Kouomou Y C，Colet P，Larger L，et al.Chaotic breathers in delayed electro－optical systems［J］.Phys Rev Lett，2005，95（20）：203903.