震蕩隨機共振的信噪比增益研究與電路仿真

任昱昊，季 冰，許麗艷，段法兵

（青島大學復雜性科學研究所，山東 青島266071）

0 引言

隨機共振是由意大利學者Benzi等在1981年發現的一種非線性現象［1］，解釋了地球每隔十萬年的冰期與暖期交替的周期性。隨機共振理論提出了一種新的觀念：噪聲不是完全有害的，而是在一定條件下，能夠增強弱信號的傳輸，提高系統對于輸入信號的反應能力，如輸出信號的信噪比。1983年，Fauve和Heslot［2］在施密特觸發器電路中證實了隨機共振現象，實驗結果表明在加性噪聲強度到達某個合適的值時，輸出信噪比會達到一個峰值。1988年，McNamara等［3］在環形激光器中同樣發現了隨機共振現象，并給出了隨機共振的絕熱近似理論。隨后，隨機共振理論與應用的研究漸漸成為30年來非線性科學領域的研究熱點之一，在電子電路系統［4－5］、神經生物學［6］、圖像語音處理［7］、神經元網絡［8］、化學反應過程［9］、地震學研究［10］等諸多領域中取得了眾多理論與實踐成果。

在電路系統和信號處理領域，隨機共振現象的相關研究已取得豐碩成果。1995年Collins等［8］研究了神經網絡信息處理模型中的并聯陣列隨機共振，將信號加入并聯的混有噪聲的子系統之后，得到比信號通過單一子系統更好的信號輸出結果。從此，陣列隨機共振的研究逐漸興起，系統結構和噪聲的積極作用相互結合提高系統性能的觀點得到重視。在相關的電路研究領域［11］，1997年，Chapeau－Blondeau和Godivier［12］提出了非線性無記憶系統中隨機共振的一般理論框架，以及系統輸出信噪比的數值計算方法。2000年，Chapeau－Blondeau［13］又發現加入非高斯噪聲誘發的陣列隨機共振方法能夠提高輸出信噪比增益。2006年，Duan等［14］證明了并聯的子系統數量趨于無窮時，輸出信噪比的計算可轉化為任意兩個子系統的統計性能分析。孫婧等［15］研究了亞閾值信號和超閾值信號通過混有噪聲的陣列子系統后的信噪比增益，證明了上述結論。2002年Chialvo等［16－17］研究了噪聲對于神經元響應的影響，發現了震蕩隨機共振現象，隨后在電路研究當中，同樣也證實了魅隨機共振現象的存在［18－19］。所謂震蕩隨機共振現象，就是將頻率分別為f＋kf0的高頻干擾加入到系統中，使得系統輸出在頻率f0處產生隨機共振，以提高系統對于含頻率f0輸入信號的響應能力。

本文是以上述研究的結果為基礎，進一步對比研究了陣列隨機共振與震蕩隨機共振在提高輸出信噪比方面的性能以及電路實現。由于實際的信號傳輸過程中，純凈的輸入信號在到達系統之前，一般會被噪聲所污染。因此，本文考慮真實的輸入由信號和外部噪聲組成的，電路系統為并聯的硬限幅子系統，硬限幅電路實在通訊、雷達等信息處理領域應用非常廣泛的一種非線性電路。在每個硬限幅子系統加入了與外部噪聲無關，強度、分布均相同，但相互獨立的內部噪聲。然后，將每個子系統的輸出取算術平均，就得到了陣列的輸出信號。輸出輸入的信噪比增益的計算結果表明，在信號、噪聲、非線性系統的協同作用下，信噪比增益存在大于1的區域，并且進一步在此電路系統中證明了無限并聯系統陣列的信噪比增益問題可由任意兩個子系統的統計性能來實現。由于實際電路系統中內部噪聲有時不能加以控制，本文還著重研究了將高頻信號看作內部噪聲（干擾）的震蕩隨機共振現象，人為添加高頻干擾到電路子系統中，進一步提高陣列的輸出輸入信噪比增益。在傳統的信號處理領域中，高頻信號往往只作為輸入信號的載波，通過調制和解調來達到信號通信的目的。而在本文當中，高頻干擾信號的作用與陣列隨機共振系統中噪聲的作用相同，研究由正弦高頻信號誘發的魅隨機共振具有實際意義與應用價值。本文對震蕩隨機共振現象進行了PSpice電路仿真，得出的結果與數值模擬相吻合，進一步在實踐層面證實了上述實驗結果。

1 并聯電路系統與信噪比增益

本文所采用的并聯電路系統是由N個并聯的硬限幅符號電路子系統組成的，每一個子系統的輸入輸出滿足關系式，這里，θ為閾值。實際電路圖如圖1所示。

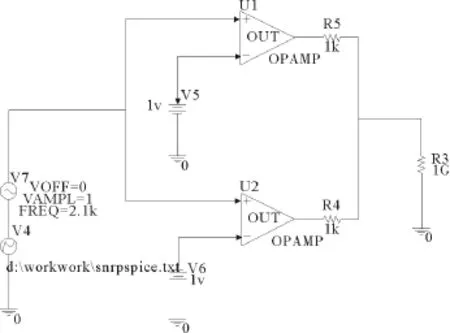
圖1 硬限幅并聯電路子系統圖（N＝1）Fig.1 The circuit diagram of a hard limiter sub－system （N＝1）

每個子系統的共同輸入都是一個正弦和噪聲的混合信號s（t）＋ξ（t），ξ（t）為外部噪聲。子系統的內部相互獨立的噪聲設為ηi（t），與ξ（t）不相關，且ηi（t）和ηj（t）強度與概率密度分布相同。則子系統的輸出可表示為

系統的總輸出y（t）可表示為

y（t）可看作其非穩態均值E［y（t）］與圍繞E［y（t）］的穩態波動（t）之和，即

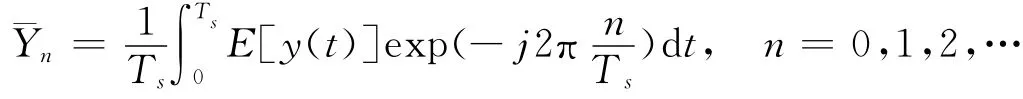
為計算系統輸出的自相關函數，引入時間延遲τ，可得二階非穩態相關函數

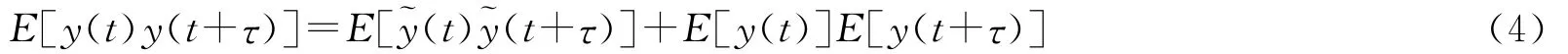
對其進行時間平均后，可得系統輸出y（t）的自相關函數Ryy（τ）

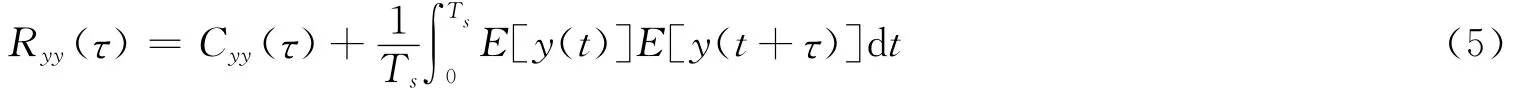
其中，自協方差函數為

由維納－辛欽定理，y（t）的功率譜密度可以計算為

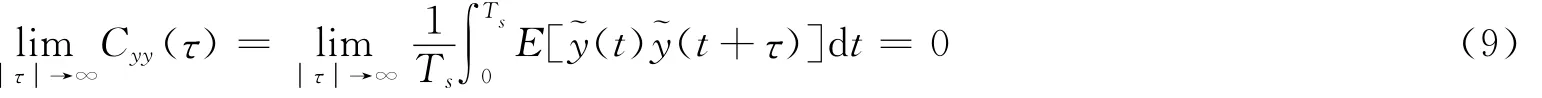
y（t）的非穩態方差可表示為var［y（t）］＝E［y~（t）y~（t＋τ）］，對其進行時間平均，可得

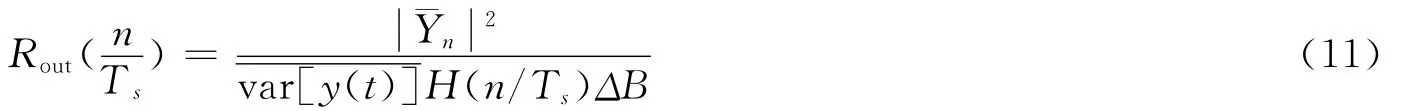
特別地，并聯的子系統數量N→∞時，有

將式（12）與（13）代入式（10）與（11）可知，并聯子系統數量N→∞時的輸出信噪比，可以由任意兩個子系統的統計性能來計算。

2 實驗結果和PSpice電路仿真

利用上述理論公式，本文對于若干硬限幅符號電路組成的并聯陣列的輸出輸入信噪比增益進行了數值仿真和PSpice電路仿真。

如圖2a所示，輸入信號為頻率f＝100Hz，幅值為0.3V的正弦信號，外部噪聲高斯白噪聲，方差給定為0.752，內部噪聲為均布噪聲。取子系統數量N＝1，2，5，10，100和∞，作出信噪比增益與內部噪聲強度的函數關系圖。從圖2a中可以看出，隨著內部均布噪聲強度增大，信噪比增益先增大，在達到最大值后又減小，出現陣列隨機共振現象。同時，隨著陣列子系統數目增加，信噪比增益也隨之增大，當子系統數目趨于無窮時，信噪比增益趨近于1。

圖2b表示了頻率為f＝100Hz，幅值為0.5V的正弦輸入信號，外部噪聲為給定方差的均布噪聲，通過調諧子系統內部均布噪聲強度，得到的陣列輸出輸入信噪比增益曲線。這里陣列數目取 N＝1，2，5，10，100和∞。從圖2b中可以看出，隨著內部噪聲強度增大，信噪比增益同樣出現隨機共振現象。特別地，當陣列數目N取10、100和∞時，圖2b中可以觀測到信噪比增益大于1的區域。

圖2 并聯陣列信噪比增益隨內部均布噪聲強度變化曲線Fig.2 SNR gain as a function of the internal uniform noise root－mean－square（RMS）amplitude

由圖2可以看出，若系統外部加入高斯噪聲，信噪比增益不會超過1，當系統外部加入了非高斯噪聲時，信噪比增益才有可能大于1［18］。這一理論結果已經在我們前期工作中進行了證明［18］，這里利用電路系統進行了實驗驗證。而且，當子系統數量N給定時，隨著系統內部噪聲強度的增加，信噪比增益出現雙峰值現象，如圖2b所示。

在電路仿真實驗中，發現對于每個子系統加入內部噪聲并對其強度進行調諧的實驗工作不容易實現，這也造成了陣列隨機共振實現增強輸出信噪比的目的難以實現。這里利用震蕩隨機共振機制對于并聯電路的性能進行改進，每個子系統中加入高頻干擾的方法是比較容易實施的。考慮輸入信號頻率為f＝100Hz，幅值為0.5V的正弦信號，外部噪聲為均布噪聲，方差給定為1／。在每個子系統內部加入如下高頻正弦干擾信號，頻率依次為（2＋0.1k）kHz，幅值為。取子系統數量N＝1，2，5，10，100，作出信噪比增益與內部噪聲強度的函數關系，如圖3所示。這里子系統內加入的正弦信號的作用類似于以往隨機共振研究中噪聲的作用，即將高頻信號看作噪聲的一種。

從圖3中可以看出，子系統內部加入高頻信號噪聲對輸入信號的影響與加入噪聲的情形類似，系統輸入輸出信噪比增益出現了共振現象。特別值得指出的是，同樣的外部噪聲和輸入信號條件下，加入高頻信號噪聲的方法優于加入非高斯噪聲，我們能夠得到更高的系統輸出輸入信噪比增益。雖然二者的信噪比增益最大值相近，都能達到1.2左右，但在圖3中，利用調諧高頻干擾幅值的方法能夠在并聯子系統數目N＝5時，得到的信噪比增益就已接近于1，當系統數目N＝100時，得到的信噪比增益就能達到加入陣列隨機共振方法中系統數目N→∞的增益水平。由圖3還可看出，與圖2中在子系統內部加入均布噪聲時的情況類似，信噪比增益同樣出現了雙峰現象。這是由于正弦信號也可看作一種具有概率密度的隨機變量，其概率密度與均勻分布的概率密度相似，都具有邊界性。另外，從實際電路設計的方便程度來講，加入特定頻率的高頻正弦干擾信號較之加入特定噪聲，更容易實現。這些優點意味著震蕩隨機共振方法比利用傳統隨機共振方法具有更加廣泛的潛在應用價值。

針對圖3中N＝1，2，5，10，100的情況，我們利用PSpice電路仿真軟件進行了實驗證實，結果如圖4和圖5所示。在圖4中，從上到下的3個圖形分別為a）輸入信號波形、b）輸入信號通過硬限幅陣列電路的輸出波形和c）通過N＝5并聯系統后的非穩態輸出均值的時間波形。由圖4b和圖4c可以看出，硬限幅并聯系統相當于一個模數轉換電路，將輸入的模擬量轉化為了具有2 N＋1個狀態的數字量。隨著并聯系統個數的增加，電路輸出的狀態能夠不斷逼近輸入信號的特征，到趨向于無窮時，從統計的角度上就能夠還原輸入信號。當然，隨著并聯陣列數目的增加，實際電路的實現也愈加困難。由圖4還可看出，系統的輸出波形出現了與信號周期f相同的漂移干擾。經研究發現，這種漂移現象是加入相同相位且頻率相差不甚大的高頻干擾導致的。當N比較小時，現象更加明顯，隨著N的增大，到N＝100時，已幾乎看不到漂移現象。這種漂移現象的周期之所以與信號周期相同，是因為信號周期是所有高頻干擾周期的公倍數，這樣造成震蕩隨機共振的同時，也產生了圖中所示的漂移干擾。要想避免或降低這類漂移，可以采取以下兩種措施：增大子系統數量N和增大高頻干擾之間的差fk－fk－1。

如圖5所示，輸入信號s（t）＝0.5sin（200πt），外部噪聲ξ（t）為強度σ2＝1的均布噪聲。內部高頻干擾η（t）＝每個子系統的頻率fN滿足fn＝（2＋0.1＊n）kHz。分別對陣列數目為N＝1，2，5，10，100的電路系統進行了PSpice仿真。圖中自下而上的連續曲線分別對應了子系統數量為N＝1，2，5，10和100時，系統輸出輸入信噪比增益隨高頻噪聲強度變化曲線。離散數據點為PSpice電路仿真得到的信噪比增益。可以看出，PSpice電路仿真所得到的結果與數值計算的結果相吻合，呈現典型的震蕩隨機共振現象，并且在合適的內部高頻干擾強度下，輸出－輸入信噪比增益可以大于1，陣列隨機共振中雙共振區域也得到了證實。

圖3 外部加均布噪聲，并聯陣列信噪比增益隨高頻干擾的強度變化曲線Fig.3 SNR gain as a function of the internal high frequency interference signal amplitude.Here，the external noise is uniform noise

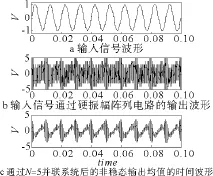
圖4 PSpice電路仿真的相關波形的強度變化曲線Fig.4 Simulation result of the PSpice simulation experiment

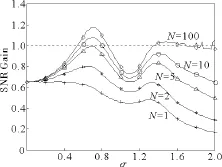
圖5 PSpice電路仿真信噪比增益隨高頻噪聲強度的變化Fig.5 SNR gain as a function of the internal high frequency interference signal amplitude in the PSpice simulation experiment

3 結論

本文著重研究了并聯陣列硬限幅電路中的震蕩隨機共振與陣列隨機共振現象，輸入信號為被噪聲污染的正弦信號，通過并聯的硬限幅電路組成的陣列，受到系統外部噪聲、系統內部高頻干擾信號、非線性電路系統的協同作用，產生了系統輸出輸入信噪比增益隨著干擾強度增加而出現峰值區域的現象。數值仿真以及PSpice電路仿真證明，當并聯子系統數目增加時，輸出輸入信噪比增益也相應增加，且信噪比增益存在大于1的區域。對子系統內部加入高頻干擾作為噪聲的震蕩隨機共振方法，與調節陣列內部噪聲強度的傳統隨機共振方法相比，能夠得到更優的信噪比增益，而且實際電路實現起來也更為簡便實用。這些研究成果印證了陣列隨機共振的相關理論，并且對利用噪聲或高頻干擾進行信號處理的應用研究具有重要意義。

本文的研究目前局限于電路并聯系統的情形，對于實際中更為復雜的子系統結構，如層次網絡結構，值得進行深入研究。噪聲或干擾僅僅考慮了高斯噪聲、均布噪聲和正弦高頻干擾，其他電子電路中常見的噪聲類型，如散彈噪聲，約翰遜噪聲等，需要做更深入的研究探討，為震蕩隨機共振的理論和實際應用提供更好的實驗證據。此外，在子系統內部加入均布噪聲和高頻干擾的實驗中，信噪比增益都呈現雙峰值現象，在今后的研究中，需要給出這類現象的理論分析與證明。

［1］ Benzi R，Sutera A，Vulpiani A.The mechanism of stochastic resonance［J］.J Phys A：Math Gen，1981，14（11）：453－457.

［2］ Fauve S，Heslot F.Stochastic resonance in a bistable system［J］.Phys Lett A，1983，97（12）：5－9.

［3］ McNamara B，Wiesenfeld K，Roy R.Observation of stochastic resonance in a ring laser［J］.Phys Rev Lett，1988，60（25）：2626－2629.

［4］ Ueda M.Improvement of signal－to noise ratio by stochastic resonance in sigmoid function threshold systems，demonstrated using a CMOS inverter［J］.Phys A，2010，389（10）：1978－1985.

［5］ Hellen E H，Dana S K，Kurths J，et al.Noise－Aided logic in an electronic analog of synthetic genetic networks［J］.PLoS ONE，2013，8（10）：e76032.

［6］ Wiesenfeld K，Moss F.Stochastic resonance and the benefits of noise［J］.Nature，1995，373（6509）：33－36.

［7］ Ditzinger T，Stadler M，Struber D，et al.Noise improve three－dimensional perception：stochastic resonance and other impacts of noise to the perception of auto stereograms［J］.Phys Rev E，2000，62（2）：2566－2575.

［8］ Collins J，Chow C，Imhoff T.Aperiodic stochastic resonance in excitable systems［J］.Phys Rev E，1995，52（4）：3 321－3 324.

［9］ 周寶晶，楊靈法，辛厚文.Pt（100）／NO ＋ CO體系隨機共振的理論研究［J］.高等學校化學學報，1999，20（3）：428－431.Zhou Baojing，Yang Lingfa，Xin Houwen.Theoretical study on stochastic resonance in Pt（100）／NO＋CO system［J］.Chemical Journal of Chinese Universities，1999，20（3）：428－431.

［10］鄭文衡，張國安，陳俊華.用隨機共振理論解釋地震孕育過程與地震發生現象中的一個顯著特征［J］.地震研究，1998，21（3）：12－15.Zheng Wenheng，Zhang Guoan，Chen Junhua.Interpretation of the remarkable character in earthquake preparation and occurrence process from the theory of random resonance［J］.Earthquake Research，1998，21（3）：12－15.

［11］Liu Z，Lai Y，Nachman A.Enhancement of noisy signals by stochastic resonance［J］.Phys Lett A，2002，297（1）：75－80.

［12］Chapeau－Blondeau F，Godivier X.Theory of stochastic resonance in signal transmission by static nonlinear systems［J］.Phys Rev E，1997，55（2）：1478－1495.

［13］Chapeau－Blondeau F.Nonlinear test statistic to improve signal detection in non－gaussian noise［J］.IEEE Signal Processing Letters，2000，7（7）：205－207.

［14］Duan F，Chapeau－Blondeau F，Abbott D.Noise－enhanced SNR gain in parallel array of bistable oscillators［J］.Electron Lett，2006，42（17）：1008－1009.

［15］孫婧，段法兵.復雜隨機系統的信噪比增益研究與陣列隨機共振［J］.復雜系統與復雜性科學，2006，3（2）：50－54.Sun Jing，Duan Fabing.Signal－to－noise ratio gain in complex random systems and array stochastic resonance［J］.Complex Systems and Complexity Science.2006，3（2）：50－54.

［16］Chialvo D R，Calvo O，Gonzalez D L，et al.Subharmonic stochastic synchronization and resonance in neuronal systems［J］.Phys Rev E，2002，65（5）：050902（R）

［17］Chialvo D R.How we hear what is not there：a neural mechanism for the missing for the missing fundamental illusion［J］.Chaos，2003，13（4）：1226－1230.

［18］Calvo O，Chialvo D R.Ghost stochastic resonance in an electronic circuit［J］.International Journal of Bifurcation and Chaos，2006，16（3）：731－735.

［19］Noguchi T，Torikai H.Ghost stochastic resonance from an asynchronous cellular automaton neuron model［J］.Circuits and Systems II：Express Briefs，2013，60（2）：111－115.

［20］Ma Y，Duan F，Chapeau－Blondeau F，et al.Weak－Periodic stochastic resonance in aparallel array of static nonlinearities［J］.PLoS ONE，2013，8（3）：e58507.