基于超網絡視角對上海軌道交通網絡的研究

孫 琳，郭進利 （上海理工大學，上海200093）

SUN Lin, GUO Jin-li (University of Shanghai for Science and Technology, Shanghai 200093, China)

0 引 言

18 世紀數學家歐拉對七橋問題的建模和分析開創了數學中圖論這一分支，此后就有很多學者利用圖論和復雜網來研究實際問題，來分析網絡中存在的問題。復雜網絡應用于對軌道交通的研究更成為熱點問題，惠偉等[1]采用復雜網絡以上海和北京公交線路為例通過計算復雜網絡的靜態特征值顯示北京和上海的公交網絡具有小世界特性。Latora 等[2]用復雜網絡對波士頓地鐵的網絡特性進行初探。汪濤[3]等對北京、上海、廣州三個城市地鐵網絡特征進行比較。楊楊[4]等對北京公共交通網絡進行建模實證分析和對蓄意攻擊做了有效的分析，有些學者對上海地鐵當前網絡和規劃網絡做了特性分析，得出重要節點不斷向外部轉移。以前的研究方式多限于研究節點與邊同質的網絡，無法完全刻畫現實網絡復雜性的特征，如生態網絡和電力網絡，前者節點不同質，后者邊不同質。隨著交通網絡的發展，出現了鐵路網、公路網、航空網等許多復雜的網絡，這些網絡節點和邊的數量眾多，結構復雜，我們已經不能用傳統的復雜網絡去研究軌道交通網絡。

超網絡也是一種特殊的復雜網網絡，它既可完美刻畫現實網絡特征，本身又為綜合網絡，故超網絡研究必將成為網絡研究新潮流。大量學者對復雜網絡進行研究，有些人擺脫了還原論的局限性，開始研究網絡與網絡之間的影響，超網絡概念就被提出。對超網絡的研究不僅有實際意義，也為研究系統的復雜性提出一種新的想法。最早使用超網絡概念與運輸系統的是Y.Sheffi[5]，而美國科學家A. Nagurney[6]在處理上述交織的網絡，把高于而又超于現存網絡的網絡稱為超網絡，使超網絡的定義開始明確。后來Berge[7-8]在1970 年提出了什么是超圖的概念，并描述了無向超圖理論，隨后研究者對超圖的超回路、著色和t-設計[9]等問題進行研究。21 世紀，大量研究者將超圖理論以超網絡的形式用于現實問題研究，如Bretto[10]用超網絡于研究圖像的處理，李曉強[11]用超網絡對基于變分不等式的電子商務進行研究，Wang Z P[12]等用超網絡來研究供應鏈，并且構建由兩個制造商、兩個分銷商和兩個需求市場組成的供應鏈超網絡模型從而解決了各層次多標準優化的問題。

基于軌道交通網絡的復雜性，本文從超網絡視角對上海軌道交通進行研究，得到用超網絡的度分布和聚類系數，分析軌道交通網絡的特性，并提出一些規劃建議。

1 超網絡的定義

目前對超網絡的研究還處于起步階段，有一些概念還沒有得到公認。但是已經有人從不同的視角來定義超網絡。目前對超網絡的定義有兩種。

1.1 H. Frank 等在文獻[13]中給出的定義

超網絡里的節點表示給定集合的網絡，而邊和弧表示在給定集合中的結合移動和結合偏好，超網絡唯一地表示由規則支配的所有結合移動和偏好。

1.2 用超圖來定義超網絡

超圖[14]定義：設V=｛v1,v2,…,vn｝是一個有限集。若：（1）

則稱二元關系H=（E,V）為一個超圖。V的元素v1,v2,…,vn稱為超圖頂點，E=｛e1,e2,e3,…,en｝是超圖的邊集合，集合e的元素eI=｛Vi1,Vi2,…,Vij｝（i=1,2,3,…,m）稱為超圖的邊。如果兩個頂點屬于同一條超邊，則稱這兩個頂點鄰接；如果兩條超邊的交集不空，稱為兩條超邊鄰接。如果一個超圖H的任意兩條超邊至多有一個公共點，則稱H為簡單超圖。

1.3 超網絡相關定義

1.3.1 關聯矩陣[14]定義

一個圖G= V,（）E的關聯矩陣B滿足下面條件：（1）B的每一行與G的頂點相關； （2）B的每一列與G的邊相關聯；（3） 如果第j個邊與第i個頂點相關聯，那么bij=1。

有n個頂點的聯通圖G的關聯矩陣的秩是n-1。在上海軌道交通中，每一行與軌道交通站點有關，每一列與軌道交通線路有關，如果行中的站點在列中的線路中則在關聯矩陣中寫1 否則寫0。

1.3.2 鄰接矩陣[14]

一個圖G= V,（）E的鄰域矩陣S，滿足下列條件：（1）S的每一行與G的頂點相關；（2）S的每一列與G的頂點相關；（3） 如果頂點vi與vj之間存在一個關系，即存在一個弧，鏈接著頂點vi與vj，那么sij=1；存在兩個弧sij=2；否則，sij=0。

在上海軌道交通超網絡中，鄰接矩陣的每行和每列都與站點有關，在站點與站點之間由地鐵形成的線路相連，當行中的站點與列中的站點在同一條線（一條弧） 中，則Aij=1。當行中站點與列中站點在共同的兩條線路（兩條弧） 中則Aij=2，如果兩個站點沒有在共同的線路中，則Aij=0。上海軌道交通的鄰接矩陣A如下。

當A22=0 表示兩個站點是同一個站點；

當A23=2 表示第2 個站點和第3 個站點有兩條共有的線路；

當A2811=0 表明第281 個站點和第1 個站點沒有在共同的線路中。

2 超網絡度

對上海軌道交通286 個站點14 條線路進行統計，得到其度分布。

2.1 節點度

節點度[15]（Node Hyperdegrees） 節點連接的頂點數計為d（）i，在軌道交通網絡中節點是每個站點，超邊是每條地鐵線路，節點度描述的是一個站點與其他站點的連接程度。上海市軌道交通超網絡的節點度分布和累計度分布如圖1、圖2 所示。

由圖1 可以看出節點度大部分在20 到40 之間，說明上海軌道交通網絡站點之間的連通程度還是很小，可以計算出上海軌道交通所有節點度的平均值為31.51049，可以參考這個數值對包含站點少的線路進行調整和改造。由圖2y=2.1408e-0.0577x可知節點度的累計分布符合指數分布。

2.2 節點超度

節點超度[15]（Node Hyperdegrees） 節點的超度定義為包含該節點的超邊個數, 記為dH（）i。在軌道交通網絡中，每個站點是節點，節點超度指的是有多少條超邊經過同個站點。上海市軌道交通超網絡的節點超度的分布和累計超度分布如圖3、圖4 所示。

由圖3 可知，軌道交通網大部分站點的節點超度值為1，占整個網絡的80%以上，表明大部分站點只有一條軌交線路經過。經計算，該網絡的平均節點超度為1.188811，說明可換成的站點還是比較少。圖4 雙對數坐標中對散點圖的擬合表明，節點度的累計概率分布p（k）服從冪律分布。網絡的擬合結果為y=1.3885x-3.8216，可見從節點超度分析可得上海軌道交通網絡具有無標度網絡的特性。

計算軌道交通超網絡節點超度和節點度按照節點超度的前11 個站點列表如表1 所示。

從表1 可知，按節點超度從大到小排列，前11 個站點相應的節點度如表1 所示。經統計，節點度和節點超度排名前10 的站點相同，金沙江站節點超度是第11，但節點度不是排名前11，說明13 號線路可以增加站點。由表1 可知前10 個站點節點度和節點超度都很大，所以這幾個站點是上海軌道交通的重要站點，應該加強對這幾個站點的保護，從而使整個交通網絡高效率運行。

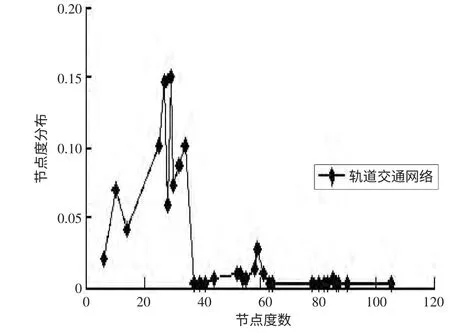
圖1 軌道交通超網絡節點度分布

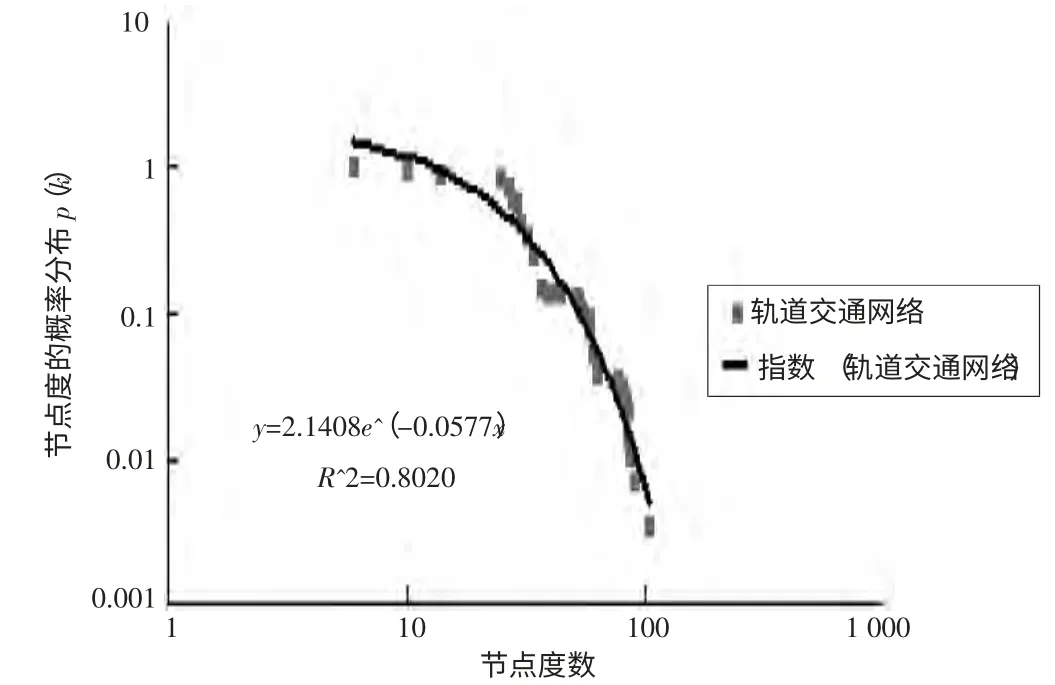
圖2 軌道交通超網絡節點度的累計概率分布

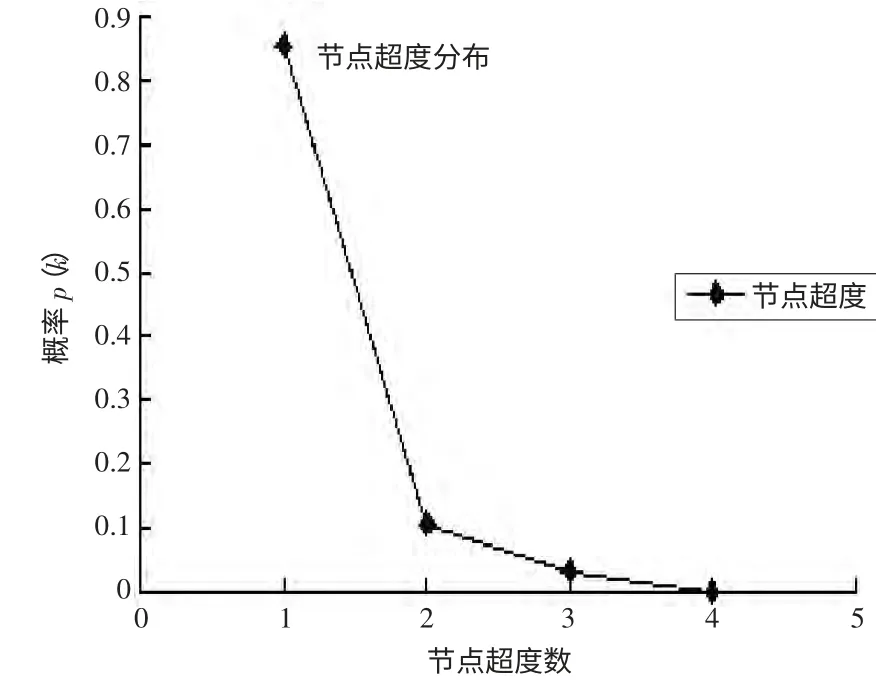
圖3 超網絡節點超度的概率分布

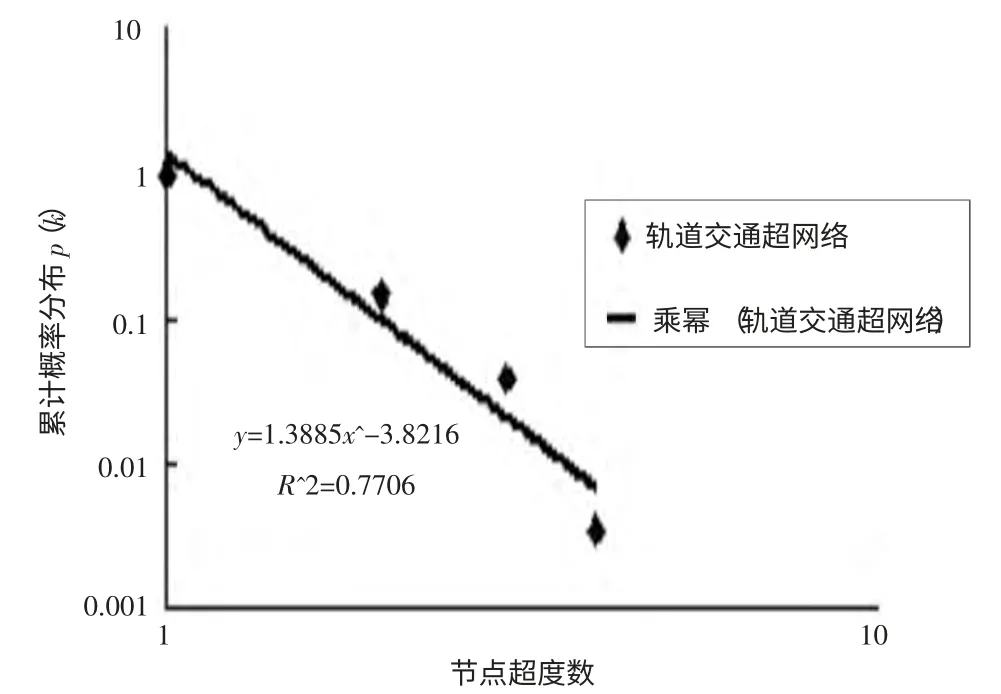
圖4 超網絡節點超度的累計概率分布

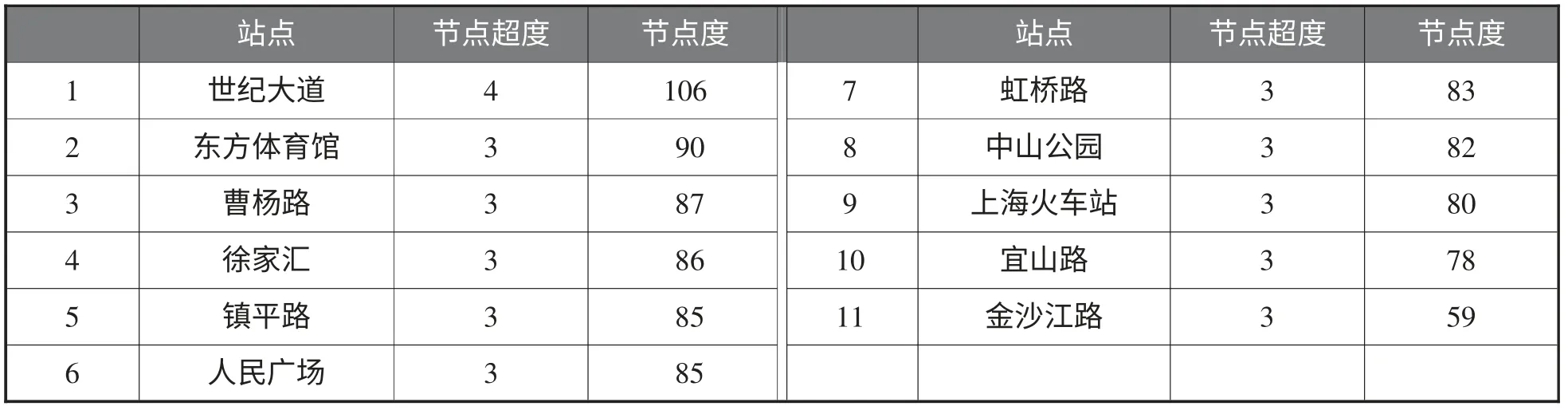
表1 站點節點度和節點超度對比表

2.3 邊超度

邊超度[15]（Hyperedge Degrees） 如果兩條超邊有相同節點，則這兩條超邊通過該節點相連。邊超度為與該超邊相連的其它超邊的數。上海市軌道交通超網絡的邊超度的分布和累計超度分布如圖5、圖6 所示。

由圖5 可知邊超度是9 的線路占的比例最大，其次是邊超度為7 的線路。說明有些線路與其他線路之間的聯系很少，比如5 號線和16 號線。像邊超度比較小的線路可以成為以后規劃的重點線路。經計算網絡的平均邊超度為6.571429，可以看出邊與邊之間的聯系還比較少，對小于平均邊超度的線路應進行調整和改造。對于邊超度較大的線路進行重點保護，以免被蓄意攻擊，導致整個交通的癱瘓。

3 軌道交通超網絡的聚集系數

H=（V,E）表示一個簡單超圖，節點集V=｛v1,v2,…,vN｝，超邊集E=｛E1,E2,…,Em｝，鄰接矩陣A（H）是對稱方陣，元素aij為連接節點vi和vj的超邊條數，主對角線上的元素為零。假設H是有N個節點的簡單超圖，它的鄰接矩陣A是一個是對稱矩陣，因此存在一個正交矩陣U=uij，使得A=UDUT，其中：D=diag（λ1,λ2,…,λn），U的列向量是與A的特征值相對應的正交向量。

設vi和vj是超圖H的兩個節點，A是H的鄰接矩陣，那么H中長度為k的從vi到vj的路徑（對應于復雜網絡，也稱為vi-vj鏈） 的個數就可以用矩陣Ak第i行第j列的元素值來表示。

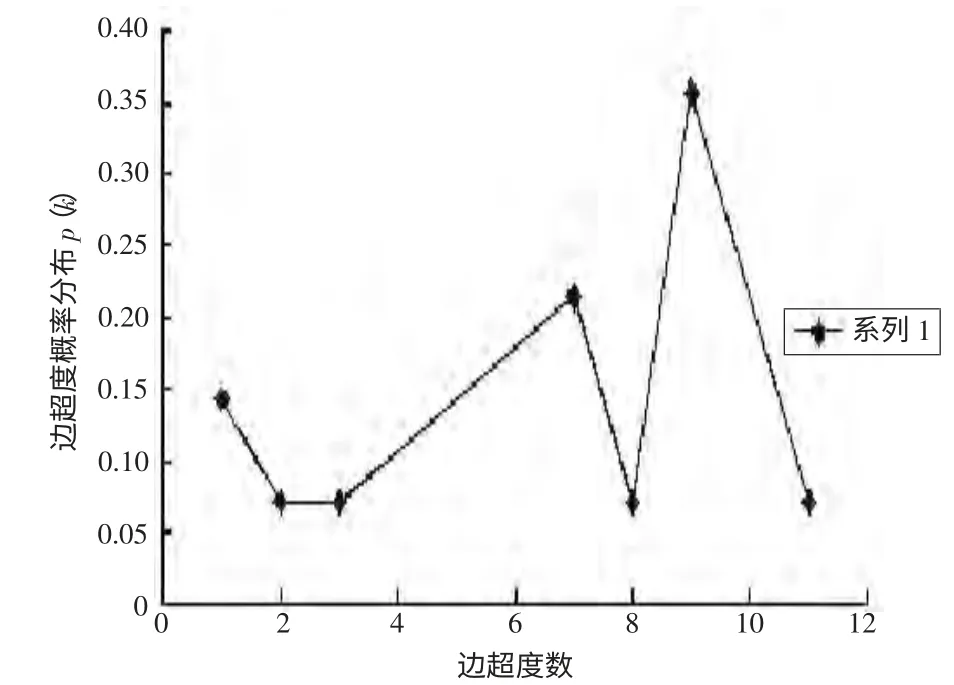
圖5 邊超度的概率分布

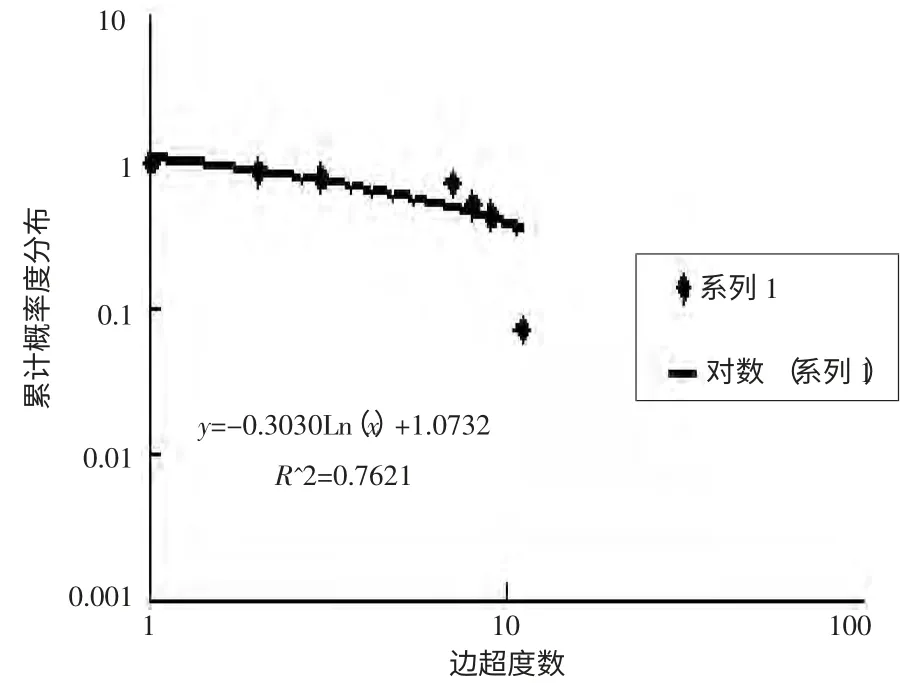
圖6 邊超度的累計概率分布

H中長度為k的vi-vj鏈的條數為因此，H中長度為k的所有鏈的條數為：

H中從vi開始最后又回到vi的長度為k的閉合鏈的條數則由給出，是Ak的第i個對角線元素的值：

那么H中長度為K的閉合鏈的總條數就是：

聚類系數的理論來源是社會學文獻中的傳遞系數：

其中分子中的6 表示一個三角形可以形成6 條長度為2 的路徑，從而保證當圖KN是完全連通圖時C2（G）=1。由于上面的結論只適合沒有重邊的簡單圖，因此當所研究的網絡中有重邊時就將其化為簡單圖再計算聚類系數，所以將（4） 式推廣到超網絡中可以得到超網絡的聚類系數[16]如下：

其中超三角形是由三個不同的節點和三條不同的超邊組成的一個序列其中這三個點彼此相連而長度為2 的路徑則形如vi,Ep,vj,Eq,vk的序列。

我們可以用長度為3 的閉合鏈的個數來計算超網絡中超三角形的個數，但是必須減去不能形成超三角形的長度為3 的閉合鏈（假超三角形） 的個數。

假超三角形形成的原理：假超三角形三個頂點在同一條超邊里。所有三條邊都是同一條超邊Ei的假超三角形個數為ti其中為超邊Ei1,Ei2,…,Eij交的基數用ai1,ai2,…,aij表示。因此假超三角形個數：

同理在計算長度為2 的路徑時，需要計算兩個節點在同一條超邊Ei的長度為2 的假的路徑數，p=6t所以超網絡的聚集系數由（1）、（3）、（5）、（6） 式可以得：

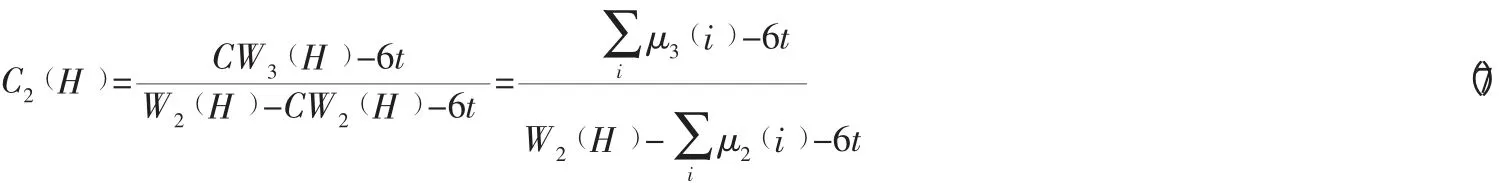
整理上式可得：

在地鐵網絡中超網絡的鄰接矩陣是286 行286 列的矩陣，由鄰接矩陣A通過Matlab 編程計算可以得到正交矩陣u=u286,286和其相對應的特征值和特征向量，從而得到：

把式（9）、（10）、（11）、（12） 代入公式（8） 中可以得到：

式（13） 中C2（H）為整個網絡的聚類系數，可以反映整個超網絡中節點的緊密性網絡的聚類一般在[0,1]之間，相對于中間值0.5 是比較小的，另外我們用超網絡來計算2020 地鐵規劃網絡的聚類系數得到0.4763668932，相對來說目前網絡的聚類系數比較小，表明目前網絡的密集度比較差，這也與我國軌道交通建設處于初級階段的情況相符。還需要更多的發展過程。

4 結論和展望

基于超網絡方法研究上海市軌道交通網絡，通過分析和研究得到以下結論:

（1） 從節點度分布和節點超度分布可以看出，上海軌道交通網絡節點超度為前10 的站點，節點度的大小也是前10，從超網絡的節點度和節點超度都可以得到世紀大道、東方體育館、曹楊路、徐家匯、鎮平路、人民廣場、虹橋路、金沙江路、中山公園、宜山路站點的節點度和節點超度都很大，說明這幾個站點是關鍵節點。但是兩種度的值又不是相同的。其中節點超度的累計度分布跟復雜網絡中的累計度分布都符合冪律分布。節點超度度大的站點是關鍵節點，如果對度大的這些站點進行蓄意攻擊，整個網絡會癱瘓。目前對超網絡的蓄意攻擊還沒有深入的研究，在后續的文章中會對超網絡的蓄意攻擊做出解釋。

（2） 從邊超度分布可以看出1、2、4、8、11 號線邊超度較大，應重點保護這幾條線，保證這幾條線路的可靠性。對于邊超度較小的線路應該進行改造和擴展，來使整個網絡的輻射半徑增大。

（3） 從聚類系數可以看出目前上海軌道交通的密集程度比較小，隨著城鎮人口的增加應加強對我國軌道交通的建設。

用超網絡研究軌道交通還處于起步階段，對于一些超網絡的靜態特征還沒有確切的定義。隨著線路的增加用超網絡的節點超度來研究交通網絡更加方便。可以將超網絡應用于全國鐵路網絡，同樣比用復雜網絡來研究全國鐵路網絡方便。當然也可以用超網絡來研究公交網絡甚至航空網絡。對于公交和地鐵網絡的換乘也提供了很好的思路。

[1] 惠偉，王紅. 復雜網絡在城市公交網絡中的實證分析[J]. 計算機技術與發展，2008(18):217-222.

[2] Latora V, Massimo M. Is the Boston Subway a small-world network[J]. Physica A, 2002,314:109-113.

[3] 汪濤，方志耕,等. 城市地鐵網絡的復雜性分析[J]. 軍事交通學院學報，2008,10(2):24-27.

[4] 楊楊，關偉. 北京市公共交通網絡復雜性分析[D]. 北京：北京交通大學（碩士學位論文），2011:59-63.

[5] Sheffi Y. Urban Transportation Networks: Equilibrium Analysis with Mathematical Programming Methods[M]. Printice-Hall,1985:33-89.

[6] Anna Nagurney, J. Dong. Supernetworks: Decision-Making for the Information Age[M]. Cheltenham Edward Elgar Publishing,2002:1-368.

[7] BERGE C. Graphs and hypergraphs[M]. New York: Elsevier, 1973:389-391.

[8] BERGE C. Hypergraphs: The theoryoffinite sets[M]. Amsterdam: Elsevier Science, 1989:1-2.

[9] TUANND. Hypergraphical t-designs[J]. Discrete Mathematics, 2006,306:1189-1197.

[10] BRETTOA, GILLIBERYL. Hypergraph-based image representation[J]. Lecture Notes in Computer Science, 2005,35:1-11.

[11] 李曉強. 基于變分不等式的電子商務超網絡研究[D]. 大連：大連海事大學（碩士學位論文），2006:8-50.

[12] Wang. Zhang FM, Wang Z T. Research on return supply chain supernetwork model based on variationalinequalities[C]//Proceeding of 2007 IEEE international conference on automation and logistics. Jinan, China, 2007:25-30.

[13] Frank H, Page J, Myrna H, et al. Networks and farsighted stability[J]. Journal of Economics Theory, 2005,120(2):257-269.

[14] 貝爾熱C，卜月華，張克民. 超圖—有限集的組合學[M]. 南京：東華大學出版社，2002:1-40.

[15] 胡楓，趙海興. 一種超網絡演化模型構建及特性分析[J]. 中國科學，2013,43(1):16-22.

[16] Estrada E, Rodrigues V R. Subgraph centrality and clustering in complex hyper-networks[J]. Phsical A, 2006,364(1):581-594.

[17] 王志平，王眾托. 超網絡理論及其應用[M]. 北京：北京科學出版社，2008:5-30.

[18] 漆玉虎，郭進利,等. 超網絡度參數研究[J]. 科技與管理，2013,15(1):34-38.