考慮維修效能的修理級別優化

樊九九，郭霖瀚，楊懿，馬麟

(北京航空航天大學 可靠性與系統工程學院，北京100191)

目前，很多學者對修理級別分析(LORA)做了大量的研究.1998年，Barros［1］提出多級多層修理級別優化模型，Barros等［2］于2001年采用分支定界法來求解該模型.2006年，Gutin等［3］提出用二分圖表示Barros修理級別優化模型，提高了解的精確性，同年Saranga等［4］將智能遺傳算法應用到修理級別優化模型中.2009年，Basten等［5］通過放松對決策變量的約束，將修理級別優化模型轉化為最小費用流模型.2011年，Basten等［6-7］正式采用最小費用流方法直接求解多級多站點的修理級別優化模型.

在庫存優化方面，Sherbrooke［8］于 1968年首次提出兩層單級備件庫存METRIC模型.1973年Muckstadt［9］將 METRIC 模型拓展為兩層兩級，建立了 MOD-METRIC 模型.1985 年，Graves［10］為兩層單級METRIC模型提出了一種更準確的近似估算法，即 VARI-METRIC 模型，而 Sherbrooke［11］于1986年將此模型(VARI-METRIC)拓展為兩級.1990年，Axsater［12］利用懲罰成本約束代替服務水平，為METRIC模型提出了另一種評估方法.Kim等［13］在2007年對傳統多級多層庫存模型中的時間分布進行拓展，提供了可修備件在一般修理時間分布下的算法.

因為修理級別分析中并不考慮基地的可用性，如果只是簡單的依次考慮修理級別和備件庫存，并不能得到最優的解決方案.于是，有些學者開始考慮將修理級別分析和備件庫存聯合優化，從而得到最優方案.1997 年，Alfredsson［14］首次建立聯合修理級別分析和備件庫存優化的兩層單級模型.2003 年，Sleptchenko 等［15］將維修能力考慮進來，提出有限維修能力下的修理級別和庫存優化模型.2011年，Basten等［16-17］對修理級別與庫存聯合優化有了深入的研究，在文獻［7］的最小費用流修理級別優化模型基礎上進行改進，分別采用邊際分析法和迭代算法求解模型.

然而，在傳統的研究中，維修時間卻極少被考慮，它是影響裝備系統可用度的重要參數.為了縮短維修時間，就需要存儲一定數量的備件.備件庫存水平的提高意味著維修時間的縮短，但同時備件配置的費用將隨之增加.優化的目標是要得到費效比最佳的修理級別及庫存配置數量，所以費用不可能無限地增長，備件庫存水平也會受到限制.因此，為了尋找維修時間最短的送修級別，并使該時間下維修費用盡可能低，需要綜合考慮維修時間和備件配置費用這兩種因素.維修時間包括凈維修時間和資源等待時間，凈維修時間指按照具體的維修步驟，完成維修保障功能所需要的實際工作執行時間，屬于固定時間;資源等待時間指保障資源配置數量有限，導致保障資源被占用而產生的等待時間，屬于變化時間.在各類資源中，等待人力人員、保障設備和保障設施的時間相當于完成故障件隊列的凈維修時間，維修完后即可完成等待;但等待備件時，由于備件需要跨站點運輸，由備件引起的等待時間將遠遠長于凈維修時間，也遠遠長于其他資源的等待時間.縮短凈維修時間或其他資源等待時間相對于整個維修時間的變化并無明顯效果，因此修理級別優化中令維修時間盡可能短主要通過縮短備件等待時間來實現.利用Little公式，可以將備件等待時間轉化為備件短缺期望數(EBO)，所以可以將維修時間-費用平衡轉化為EBO-費用平衡.本文以EBO為目標函數，費用為約束條件，建立考慮維修時間的修理級別與備件庫存聯合優化的模型.

1 優化模型

1.1 建模分析

本文分析了單層三級保障系統，如圖1所示.

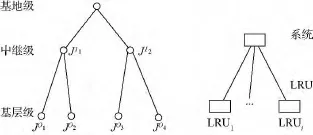
圖1 單層三級保障結構Fig.1 Single-indenture three-echelon support organization

本文修理級別優化問題建立在多級保障組織的結構中，需求數、在修件數和短缺數的隨機傳遞過程在各級保障組織間相互影響，研究這些影響關系是建模的前提(見圖2).

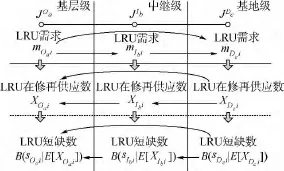
圖2 LRU需求數、在修件數和短缺數的隨機傳遞關系Fig.2 Stochastic transitive relation of demand，in-repairing and backorder of LRU

在保障組織各級別站點中，備件需求序列都服從均值為該站點需求率的平穩隨機過程，修理級別間需求過程的傳遞關系通過各級別站點需求過程的數字特征相互聯系.

在多級保障組織中，當有故障件到達時，故障件送至各級別維修均有一定的概率.若選擇基層級進行維修，則第i個外場可更換單元(LRU)在基層級Oa站點產生的備件需求率:

第i個LRU在中繼級Ib站點的需求率:

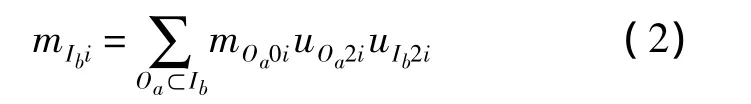
第i個LRU在基地級Dc站點的需求率:

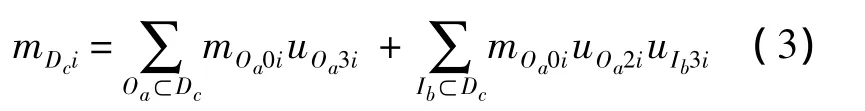
式中，mOa0i表示第i個LRU在外場Oa站點的實際備件需求數量;uOa1i表示第i個LRU在基層級Oa站點維修的概率;uOa2i表示基層級Oa站點的第i個LRU送至中繼級Ib站點維修的概率;uOa3i表示基層級Oa站點的第i個LRU送至基地級Dc站點維修的概率;uIb2i表示第i個LRU送至中繼級Ib站點后在本級維修的概率;uIb3i表示第i個LRU送至中繼級Ib站點后再送至基地級Dc站點維修的概率.

根據帕爾姆定理［18］可知，若備件的需求率服從均值為m的泊松過程，各故障件的維修周轉時間為均值T，且分布相互獨立，則在修件數服從均值為mT的泊松分布.

第i個LRU在基層級Oa站點的在修件期望數:

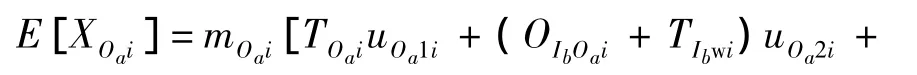
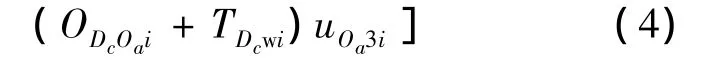
第i個LRU在中繼級Ib站點的在修件期望數:

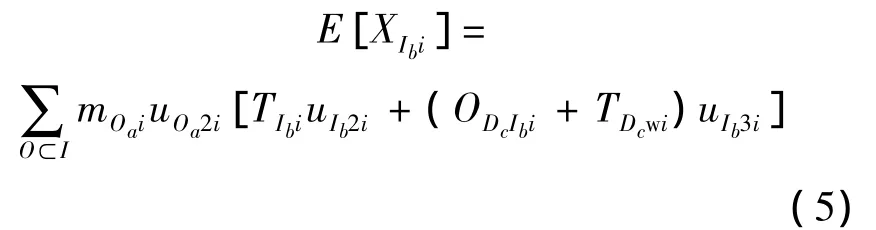
第i個LRU在基地級Dc站點的在修件期望數:

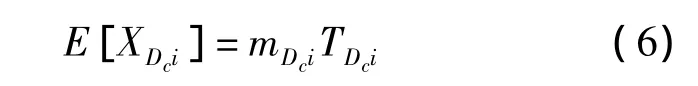
式中，TOai，TIbi，TDci分別表示第 i個 LRU 在基層級Oa站點、中繼級Ib站點和基地級Dc站點的維修時間;TOawi，TIbwi，TDcwi分別表示基層級 Oa站點、中繼級Ib站點和基地級Dc站點等待第i個LRU備件補給的時間;OIbOai表示第i個LRU在基層級Oa站點和中繼級Ib站點之間的往返時間;ODcOai表示第i個LRU在基地級Dc站點和基層級Oa站點之間的往返時間;ODcIbi表示第i個LRU在基地級Dc站點和中繼級Ib站點之間的往返時間.

需求到達后，高級別站點將對提出LRU需求的低級別站點進行補給，若該站點庫存不足，則出現短缺.

第i個LRU在基層級Oa站點的備件期望短缺數:

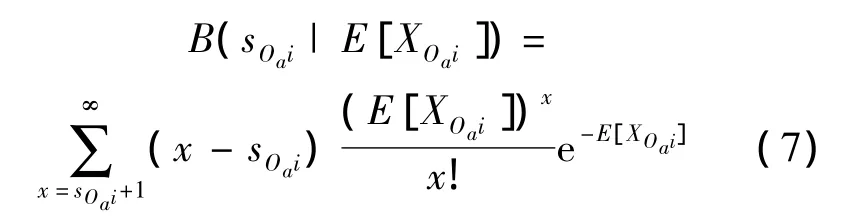
第i個LRU在中繼級Ib站點的備件期望短缺數:

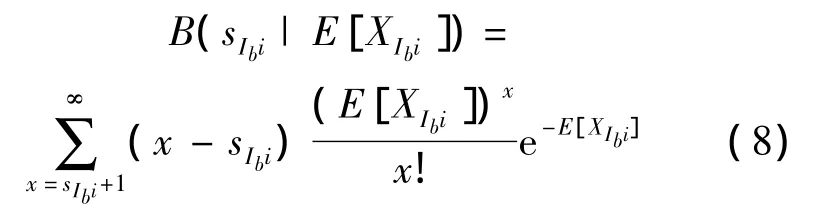
第i個LRU在基地級Dc站點的備件期望短缺數:

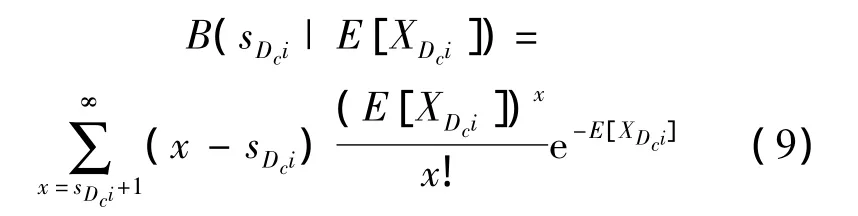
式中sOai，sIbi和sDci分別為第i個LRU在基層級Oa站點、中繼級Ib站點和基地級Dc站點的庫存數.

修理級別優化問題關注的是基層級的備件等待時間，根據Little公式，平均等待備件時間可以通過期望備件短缺數EBO除以備件需求率計算得出，即

式中，Tw為備件等待時間;m為備件需求量.結合多級保障組織多層產品結構中備件期望短缺數的傳遞過程，推導得到基層級LRU的期望短缺數，代入式(10)得到基層級Oa站點、中繼級Ib站點和基地級Dc站點的第i個LRU的等待時間.

1.2 目標函數及建模條件

本文主要是考慮維修時間的修理級別與庫存聯合優化，要權衡維修時間(主要是備件等待時間)和費用之間的關系.在引言中，已經分析了本模型的目標函數是EBO，而EBO是由備件等待時間轉化而來的.因此優化模型的實際目標函數是備件的平均等待時間.現推導以目標函數為前提的平均等待時間與EBO之間的關系.

在多級保障組織中，平均等待時間是指基層級各站點平均等待時間按各自需求率加權的平均值，如式(11):

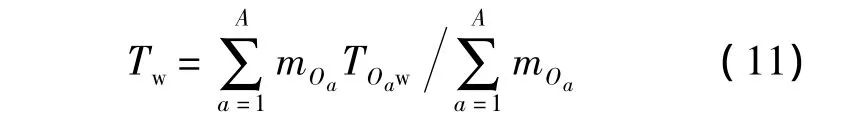
式中，mOa為基層級Oa站點的需求率，為該站點各類LRU需求率之和，即為第 i個LRU在基層級Oa站點的種類數;TOaw為基層級Oa站點的平均等待時間，同理可利用式(11)由該站點各類 LRU平均等待時間計算而得.根據式(10)，可得

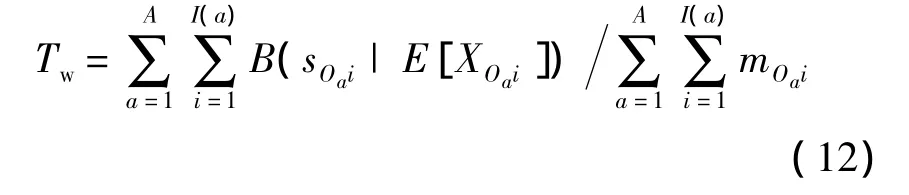
由式(12)可知，當需求率已知時，令平均等待時間Tw最小相當于令最小，即為本模型目標函數.

本模型的維修活動在以下條件下進行:

1)LRU故障時間服從指數分布;

2)庫存策略為可修產品的及時送修策略——(s－1，s)策略;

3)除備件外，其他維修資源均供應充足且維修都是成功的.

1.3 多級優化模型

經引言分析，本優化模型的約束條件需要考慮維修費用和決策變量兩類約束.

維修費用包括資源費用和備件費用.在資源費用方面，由于假設維修都是成功的，使得維持維修能力所需的資源費用也為固定值，無優化效果.在建立關于費用約束的不等式時，從費用上限中可以將此部分費用略去，費用不等式方程兩邊也不會受到影響.在備件費用方面，按模型的中間變量，即庫存配置數量計算備件配置的總費用.將維修費用限定在一定范圍內，構造維修費用的約束式，如式(13):

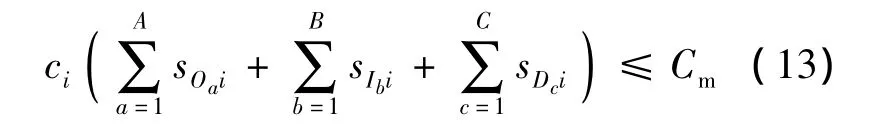
式中，ci為第i個LRU的單位購置成本;Cm為費用上限.

在決策變量約束方面，包含3部分內容:①由于優化建模要得出的是確定的修理級別，所以各變量均為0-1變量，1表示在該站點維修，0表示不在該站點維修，這部分約束如式(14)所示;②對故障LRU，只能送往基層級、中繼級和基地級中的某一個級別，如式(15)所示;③當故障LRU被送往中繼級維修時，可選擇在中繼級本地維修，也可選擇送往基地級維修，如式(16)所示.

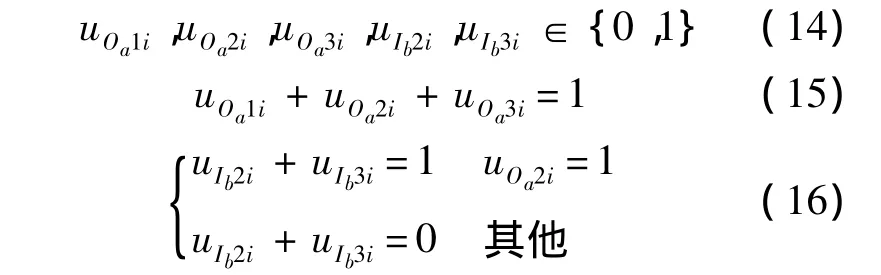
綜上，本模型可以表示為

2 優化算法

2.1 優化目標函數B(s，u)分析

相對于傳統METRIC模型中目標函數B(s)，本文引入送修決策變量u后，期望備件短缺數函數不再以庫存為唯一變量，而是以庫存數s和送修級別u為變量的二維變量函數B(s，u).盡管EBO在庫存維表現出凸函數特性，但在送修級別維的函數性質并不明確.

下面選擇三級保障組織單項備件為對象，驗證B(u)的函數特性.

設各級修理級別僅有一個站點，LRU送往基層級、中繼級和基地級維修的概率向量為u={u1，u2，u3}，且均為0-1 變量.設各級別站點備件庫存數為0，則期望短缺數與該站點的需求數相等，3種取值下基層級期望短缺數分別為

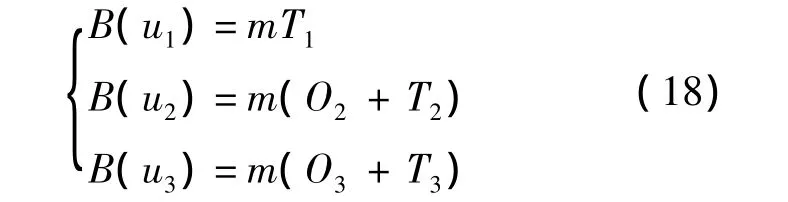
式中，T1，T2，T3分別為基層級、中繼級和基地級的維修時間;O2，O3分別為基層級與中繼級和基地級之間的申領交貨時間.令B(u3)＞B(u2)＞B(u1)，則

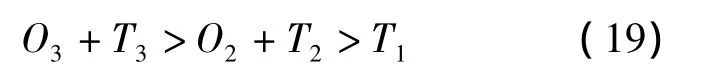
二階差分的計算式為

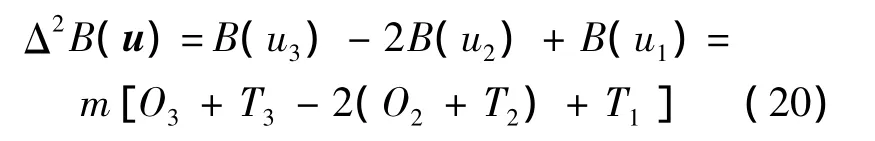
調整站點間的距離或定義適當的維修時間，都能使Δ2B(u)＜0同時滿足式(19)，因此B(u)為非凸函數.按照凸優化算法的原理，以庫存數s和送修級別組合u為變量的二維變量函數B(s，u)在實施凸優化算法時需要對庫存數和送修級別分別進行遍歷.B(u)為非凸函數，說明加入送修級別變量后，優化問題的尋優路徑受到了影響，進而影響到凸優化算法的應用，需要對函數進行重構或對算法進行改進.

2.2 算法分析

由于對各類備件的送修級別組合進行遍歷時，送修級別組合循環嵌套在備件種類循環內，所以，若在遍歷備件種類之前，已按送修級別決策變量構造出各類備件的EBO凸曲線，則各類備件按其單位費用效應邊際量迭代可以進行凸優化.因此，解決非凸函數優化算法的關鍵在于:為各類備件以送修級別為唯一變量的非凸函數B(u)分別構造凸函數.

構造每類備件的修理級別凸函數的過程與構造B(u)-C費用優化曲線的方法相同，也是利用增加該類備件產生的單位費用效應進行尋優決策.對于某一類備件，可能有多種送修級別可供選擇，此時相當于固定B(s，u)中的庫存s，比較哪種選擇產生的B(u)最小，在追加備件庫存的每一步都選擇產生最小B(u)的送修級別，則可產生最優的B(u)-C凸曲線.

用B(u)-C凸曲線上的點進行各類備件間的優化分析，得到的將是B(s，u)-C最優曲線.采用邊際分析法，生成B(s，u)-C費用最優曲線.算法步驟如下:

步驟1 初始化庫存數量si=0，?i;

步驟2 獲取各類備件在各站點的送修級別以及在各站點的EBO;

步驟3 構造各類備件在送修組合下的凸曲線;

步驟4 對各類備件凸曲線上的數據計算EBO-費用的邊際效應值Δ;

步驟5 選擇Δ最高的備件和修理級別配置備件;

步驟6 檢查是否超出費用約束，若未超出，返回步驟2，否則停止.

3 應用案例

本文示例以裝備的維修規劃為背景，介紹針對關鍵LRU部件，如何按照本文提出的修理級別優化理論，應用凸規劃優化算法，進行保障系統修理級別分析、建模、求解和驗證工作.

在本案例中，建立如圖1所示的單層三級優化模型.一個基地級有兩個中繼級(I1和I2)，每個中繼級有兩個基層級(O1，O2和 O3，O4).在每個基層級部署10個系統，每個系統由4類LRU組成.考慮到每個站點所處環境不同、系統使用情況不同，故同類LRU在不同站點需求率不同，不同站點維修能力不同(修理時間).利用Simlox軟件對4個基層級的40個系統執行1年任務進行仿真驗證，輸入數據如表1所示.

輸出結果:費用約束是100萬元;目標函數EBO優化值為2.3.最優修理級別如表2所示.

LRU在各級站點的最優庫存配置如表3所示.

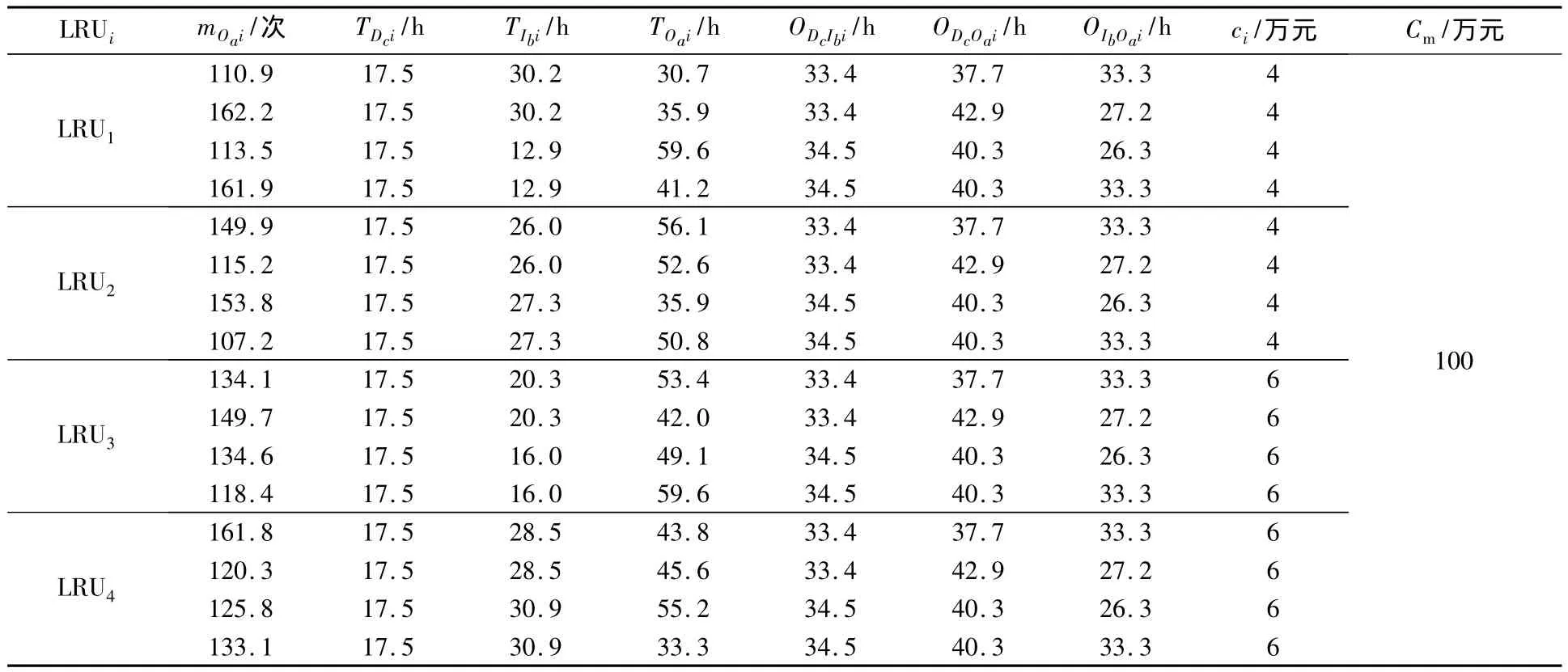
表1 多站點多類LRU的輸入數據Table1 Input data of multi-station multi-type LRU

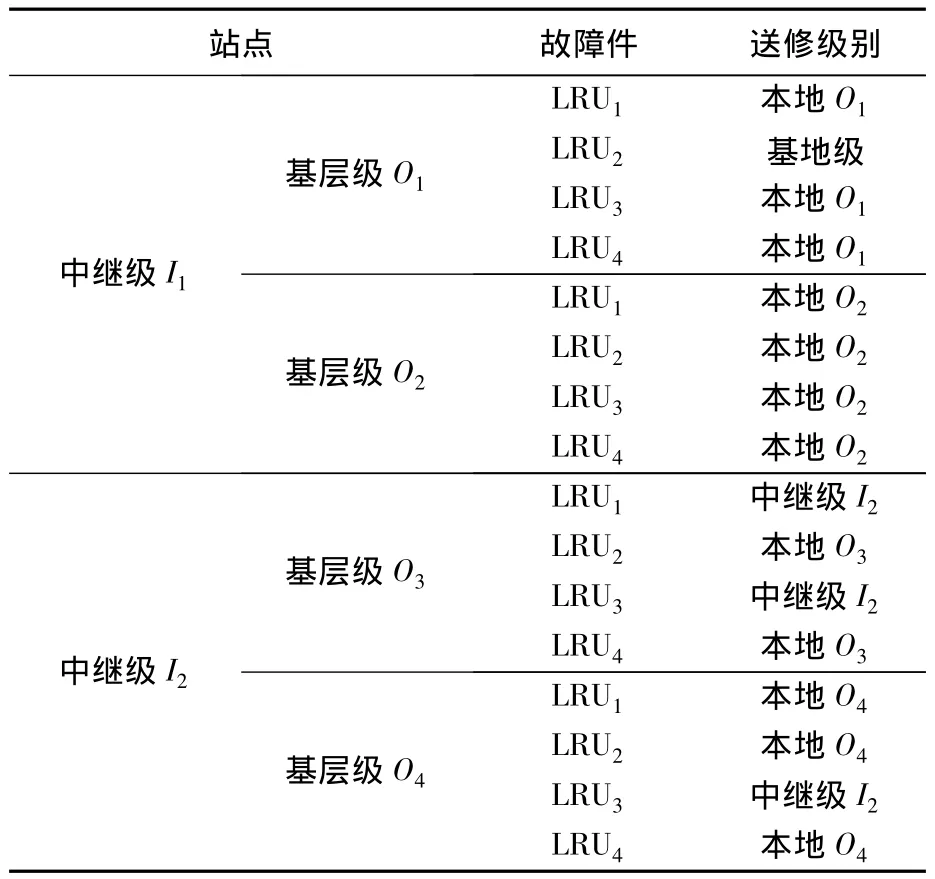
表2 各類各站點LRU最優修理級別Table2 Optimal level of repair of LRU in each station and each type

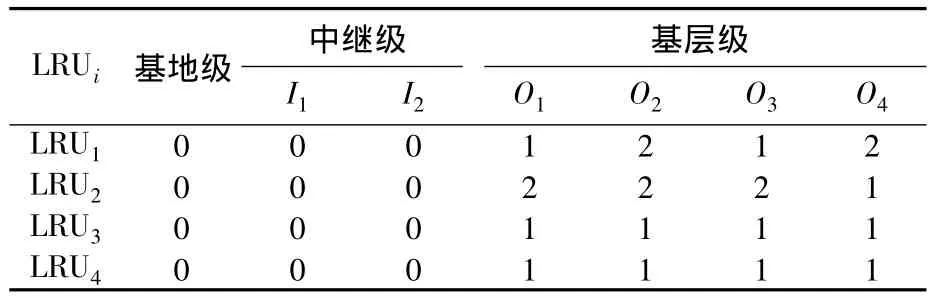
表3 各備件最優庫存配置Table3 Optimal inventory allocation of each spare

如圖3所示為EBOi-C曲線和EBO-C曲線.

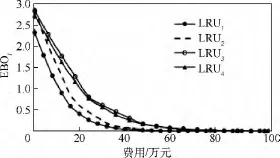
圖3 各類LRU優化曲線Fig.3 Optimal curves of each LRU

從圖3中可以看出4類LRU在總費用約束下分別得出的EBO優化曲線，在圖4中展示了4類LRU的綜合 EBO優化曲線.在圖5中，以表1的數據、表2的最優修理級別和表3的庫存配置作為仿真輸入，利用Simlox軟件，對利用本文所提出算法及模型算出的EBO進行仿真驗證，可以得出仿真EBO為2.7，而理論計算值為2.3，兩者之間相差很近，即可證明本文算法的正確性.

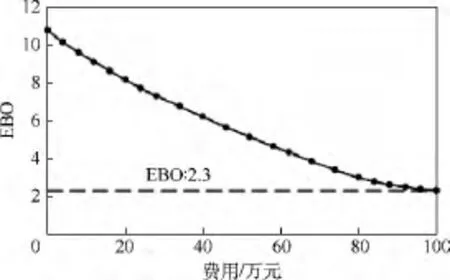
圖4 多類LRU綜合優化曲線Fig.4 Comprehensive optimal curve of multi-type LRU

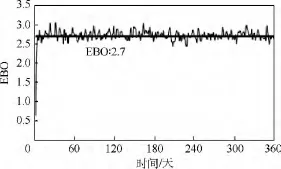
圖5 多類LRU優化和仿真曲線Fig.5 Optimization and simulation curve ofmulti-type LRU

4 結論

本文提出了一種在復雜裝備保障系統中重點考慮維修效能的修理級別分析方法，建立了備件庫存與修理級別分析聯合優化模型.

1)根據本文所提出模型和算法，能夠對復雜裝備保障系統中的修理級別和備件進行優化.

2)本文所設計的多變量凸優化算法能夠解決大規模站點群數量和備件數量的循環嵌套運算.

3)利用本模型所得出的最優修理級別和庫存配置，通過Simlox軟件仿真，比較目標函數值EBO的仿真和理論計算結果，證明了本文所提出的模型和算法的正確性.

下一步的工作將著眼于考慮更多的維修資源以及資源相關性，建立有限維修能力的優化模型.

References)

［1］ Barros L L.The optimization of repair decisions using life-cycle cost parameters［J］.IMA Journal of Mathematics Applied in Business ＆ Industry，1998，9(4):403-413.

［2］ Barros L L，Riley M.A combinatorial approach to level of repair analysis［J］.European Journal of Operational Research，2001，129(2):242-251.

［3］ Gutin G，Rafiey A，Yeo A，et al.Level of repair analysis and minimum cost homeomorphisms of graphs［J］.Discrete Applied Mathematics，2006，154(6):881-889.

［4］ Saranga H，Kumar U D.Optimization of aircraft maintenance/support infrastructure using genetic algorithm-level of repair analysis［J］.Annals of Operations Research，2006，143(1):91-106.

［5］ Basten R J I，Schutten J M J，Heijden M C.An efficient model formulation for level of repair analysis［J］.Annals of Operations Research，2009，172(1):119-142.

［6］ Basten R J I，Heijden M C，Schutten J M J.An efficient model formulation for level of repair analysis［J］.Annals of Operation Research，2009，172(1):119-142.

［7］ Basten R J I，Van der Heijden M C，Schutten J M J.A minimum cost flow model for level of repair analysis［J］.International Journal of Production Economics，2011，133(1):233-242.

［8］ Sherbrooke C C.METRIC:a multi-echelon technique for recoverable item control［J］.Operations Research，1968，16(1):122-141.

［9］ Muckstadt J A.A model for a multi-item，multi-echelon，multiindenture inventory system［J］，Management Science，1973，20(4):472-481.

［10］ Graves S C.A multi-echelon inventory model for a repairable item with one-for-one replenishment［J］.Management Science，1985，20(4):472-481.

［11］ Sherbrooke C C.VARI-METRIC:improved approximations for recoverable item control［J］.Operations Research，1986，34(2):311-319.

［12］ Axsater S.Simple solution procedures for a class of two-echelon inventory problem［J］.Operations Research，1990，38(1):64-69.

［13］ Kim J S，Shin K C，Park S K.An algorithm for repairable item inventory system with depot spares and general repair time distribution［J］.Applied Mathematical Modelling，2007，31(5):795-804.

［14］ Alfredsson P.Optimization of multi-echelon repairable item inventory system with simultaneous location of repair facilities［J］.European Journal of Operational Research，1997，99(3):584-595.

［15］ Sleptchenko A，Heijden M C，Harten A.Trade-off between inventory and repair capacity in spare part networks［J］.Journal of the Operations Research Society，2003，54(3):263-272.

［16］ Basten R J I，Van der Heijden M C，Schutten J M J.Practical extensions to a minimum cost flow model for level of repair analysis［J］.European Journal of Operational Research，2011，211(2):333-342.

［17］ Basten R J I，Heijden M C，Schutten J M J.Joint optimization of level of repair analysis and spare stocks［J］.European Journal of Operational Research，2012，222(3):474-483.

［18］ Sherbrook C C.Optimal inventory modeling of systems:multiechelon techniques［M］.2rd ed.New York:Kluwer Academic Publishers，2004:22-22.