疲勞壽命分散系數(shù)的確定與應(yīng)用研究
楊 俊,王 建,祁圣英
疲勞壽命分散系數(shù)的確定與應(yīng)用研究
楊 俊,王 建,祁圣英
(空軍西安局某軍事代表室,西安710021)
疲勞壽命分散系數(shù)是評(píng)估飛機(jī)結(jié)構(gòu)疲勞壽命與航空發(fā)動(dòng)機(jī)輪盤壽命試驗(yàn)的重要技術(shù)參數(shù)之一。闡述了國(guó)內(nèi)外疲勞壽命分散系數(shù)研究的成果,針對(duì)工程中實(shí)際壽命分布問題中最常見的對(duì)數(shù)正態(tài)分布和威布爾分布的形式,給出了基于試驗(yàn)樣本最差、中值、最好及第k試驗(yàn)壽命的分散系數(shù)表達(dá)式;重點(diǎn)分析總結(jié)對(duì)數(shù)正態(tài)分布標(biāo)準(zhǔn)差和威布爾分布中形狀參數(shù)的選取,同應(yīng)力多危險(xiǎn)部位分散系數(shù)研究及其隨應(yīng)力的變化規(guī)律;通過2個(gè)例子分析了疲勞分散系數(shù)在輪盤低循環(huán)疲勞壽命工程計(jì)算中的應(yīng)用,認(rèn)為疲勞壽命分散系數(shù)應(yīng)在不同溫度和應(yīng)變比,對(duì)數(shù)正態(tài)分布標(biāo)準(zhǔn)差,同應(yīng)力多危險(xiǎn)部位,3參數(shù)的威布爾分布,工程化應(yīng)用等方面開展進(jìn)一步研究。
疲勞壽命;分散系數(shù);對(duì)數(shù)正態(tài)分布;威布爾分布;輪盤;航空發(fā)動(dòng)機(jī);飛機(jī)
0 引言
疲勞壽命分散系數(shù)研究起源于飛機(jī)結(jié)構(gòu)疲勞壽命,根據(jù)飛機(jī)結(jié)構(gòu)失效的分布規(guī)律和中值壽命定義,借助于概率推導(dǎo)出可靠度和分散系數(shù)之間的函數(shù)表達(dá)式[1]。而近些年來(lái),基于小子樣數(shù)據(jù)的分散系數(shù)法成為航空發(fā)動(dòng)機(jī)輪盤壽命試驗(yàn)評(píng)估主要方法之一[2-3]。多年來(lái)針對(duì)疲勞壽命分散系數(shù)進(jìn)行了大量研究[1-4],使得構(gòu)件壽命分散系數(shù)可靠性評(píng)估法逐漸形成體系,并制定了各自的規(guī)范。在疲勞壽命分散系數(shù)研究中主要針對(duì)服從對(duì)數(shù)正態(tài)分布[3,5]和威布爾分布的分散系數(shù)[6]。目前除了對(duì)數(shù)正態(tài)分布標(biāo)準(zhǔn)差的選擇[7]及威布爾分布形狀參數(shù)[8]的選擇外,重點(diǎn)集中在同應(yīng)力多危險(xiǎn)部位的分散系數(shù)研究[9]及其隨應(yīng)力或應(yīng)變的變化規(guī)律[10]。
本文研究分析了疲勞壽命分散系數(shù)在飛機(jī)結(jié)構(gòu)疲勞壽命和航空發(fā)動(dòng)機(jī)輪盤壽命的應(yīng)用評(píng)估;并且確定了輪盤疲勞安全循環(huán)壽命。
1 疲勞壽命分散系數(shù)定義
文獻(xiàn)[1]將疲勞壽命分散系數(shù)定義為中值壽命N50與 Np,γ的比值

式中:N50為疲勞壽命隨機(jī)變量的總體均值,為理論值;Np,γ為在一定可靠度p和置信度γ下的壽命估計(jì)值。
式(1)顯示的是理論分散系數(shù)。而試驗(yàn)壽命分散系數(shù)

式中:[N50]t為中值試驗(yàn)壽命。
2 疲勞壽命分散系數(shù)在飛機(jī)結(jié)構(gòu)疲勞壽命評(píng)估中的應(yīng)用
很多國(guó)家都對(duì)疲勞壽命分散系數(shù)進(jìn)行研究,并提出基于對(duì)數(shù)正態(tài)分布的疲勞壽命分散系數(shù)的計(jì)算公式。
美國(guó)計(jì)算的分散系數(shù)

澳大利亞和英國(guó)計(jì)算的分散系數(shù)

式中:p為給定可靠度;γ為給定置信度;μp和μγ分別為可靠度與置信度標(biāo)準(zhǔn)正態(tài)偏量系數(shù);σ0為已知標(biāo)準(zhǔn)差;n為試驗(yàn)次數(shù)。
式(3)沒有考慮試驗(yàn)件數(shù)對(duì)分散系數(shù)的影響,因此不適宜處理疲勞試驗(yàn)結(jié)果。也沒考慮置信度的問題,即沒有考慮用少數(shù)子樣的試驗(yàn)結(jié)果代替母體真值的影響。式(4)雖然考慮了試驗(yàn)件數(shù)對(duì)分散系數(shù)的影響,但沒有考慮置信度的問題,同樣沒有考慮用少數(shù)子樣的試驗(yàn)結(jié)果代替母體真值的影響。中國(guó)也對(duì)疲勞壽命分散系數(shù)做了大量研究,高鎮(zhèn)同院士和傅惠民教授等假設(shè)“對(duì)數(shù)疲勞壽命遵循正態(tài)分布”,推導(dǎo)了基于中值試驗(yàn)壽命的分散系數(shù)計(jì)算公式[1],給出了材料疲勞試驗(yàn)統(tǒng)計(jì)分析方法,并行成中國(guó)的行業(yè)標(biāo)準(zhǔn);張福澤院士[4]在此基礎(chǔ)上對(duì)分散系數(shù)的分類和取值作了詳細(xì)論述,并對(duì)一些國(guó)家的分散系數(shù)取值差別和計(jì)算公式進(jìn)行評(píng)述。

式(5)同時(shí)考慮可靠度、置信度和試驗(yàn)次數(shù)對(duì)分散系數(shù)的影響,處理疲勞試驗(yàn)結(jié)果比較合理和完善。近些年,賀小帆、劉文廷[9]等給出了服從威布爾分布和基于中值試驗(yàn)壽命的分散系數(shù)計(jì)算公式,并與服從對(duì)數(shù)正態(tài)分布條件下得到的分散系數(shù)進(jìn)行了比較,為疲勞壽命服從雙參數(shù)威布爾分布的民機(jī)結(jié)構(gòu)確定分散系數(shù)提供技術(shù)依據(jù);陸山、楊劍秋[11]推導(dǎo)出了服從對(duì)數(shù)正態(tài)分布的基于小子樣最差和最好試驗(yàn)結(jié)果的壽命分散系數(shù)法;王衛(wèi)國(guó)[3]研究了服從威布爾分布的小子樣疲勞壽命分散系數(shù);盧小艷[8]研究了服從威布爾分布和對(duì)數(shù)正態(tài)分布,基于任意第k試驗(yàn)疲勞壽命分散系數(shù)的計(jì)算公式,為試驗(yàn)評(píng)估構(gòu)件概率壽命提供了研究方法和理論依據(jù)。
3 疲勞壽命分散系數(shù)在航空發(fā)動(dòng)機(jī)輪盤壽命評(píng)估中的應(yīng)用
輪盤(壓氣機(jī)盤或渦輪盤)是航空發(fā)動(dòng)機(jī)關(guān)鍵件,其壽命可靠性要求高,常常是制約整個(gè)發(fā)動(dòng)機(jī)壽命的瓶頸。目前,輪盤壽命可靠性評(píng)定采用數(shù)值模擬法和試驗(yàn)評(píng)估法2大類方法。試驗(yàn)評(píng)估法通過零部件在適當(dāng)?shù)妮d荷譜下的低循環(huán)疲勞試驗(yàn),再選擇一定可靠度和置信度下的分散系數(shù)來(lái)獲得輪盤的概率壽命,即常用的技術(shù)壽命。與飛機(jī)結(jié)構(gòu)疲勞壽命相比,航空發(fā)動(dòng)機(jī)輪盤壽命評(píng)估常采用最差或最好試驗(yàn)壽命與可靠壽命之比的壽命分散系數(shù)。
英國(guó)國(guó)防標(biāo)準(zhǔn)00-971指出,航空發(fā)動(dòng)機(jī)輪盤在工程上采用的壽命分布形式主要有對(duì)數(shù)正態(tài)分布和威布爾分布,并給出壽命符合對(duì)數(shù)正態(tài)分布,可靠度p=99.87%、置信度γ=95%時(shí),基于小子樣最差、最好或中值試驗(yàn)壽命的分散系數(shù),但僅限于壽命Nmax/Nmin=6,即對(duì)數(shù)壽命方差σ=0.13的特殊情形。美國(guó)在JSGC-87231A中給出服從雙參數(shù)威布爾分布的分散系數(shù)典型值。但2條文獻(xiàn)中均未給出詳細(xì)的計(jì)算公式。目前中國(guó)航空發(fā)動(dòng)機(jī)零部件的實(shí)際壽命散度可能與上述2條文獻(xiàn)條件有差別,因此,許多情況下不能直接引用2條文獻(xiàn)中的壽命分散系數(shù)。下面列舉了一些中國(guó)專家研究的成果。
3.1 基于對(duì)數(shù)正態(tài)分布的分散系數(shù)
3.1.1 基于對(duì)數(shù)正態(tài)分布分散系數(shù)公式確定
文獻(xiàn)[5]列出服從對(duì)數(shù)正態(tài)分布的基于中值壽命的散度系數(shù)計(jì)算公式,并推導(dǎo)了基于最差和最好試驗(yàn)壽命的分散系數(shù)計(jì)算公式。
(1)基于子樣中位壽命N50的分散系數(shù)計(jì)算見式(5)。
(2)基于子樣最差壽命N(1)的分散系數(shù)

(3)基于子樣最好壽命N(n)的分散系數(shù)

結(jié)果表明,中值壽命及最差試件的試驗(yàn)壽命的壽命分散系數(shù)與英國(guó)國(guó)防標(biāo)準(zhǔn)00-971相應(yīng)結(jié)果吻合較好,但最好試件試驗(yàn)壽命分散系數(shù)隨子樣數(shù)增加而增大,見表1。文獻(xiàn)[3]基于最大試驗(yàn)壽命的分散系數(shù)應(yīng)隨試件數(shù)的增加而單調(diào)增大,表1給出的壽命分散系數(shù)值更加合理。
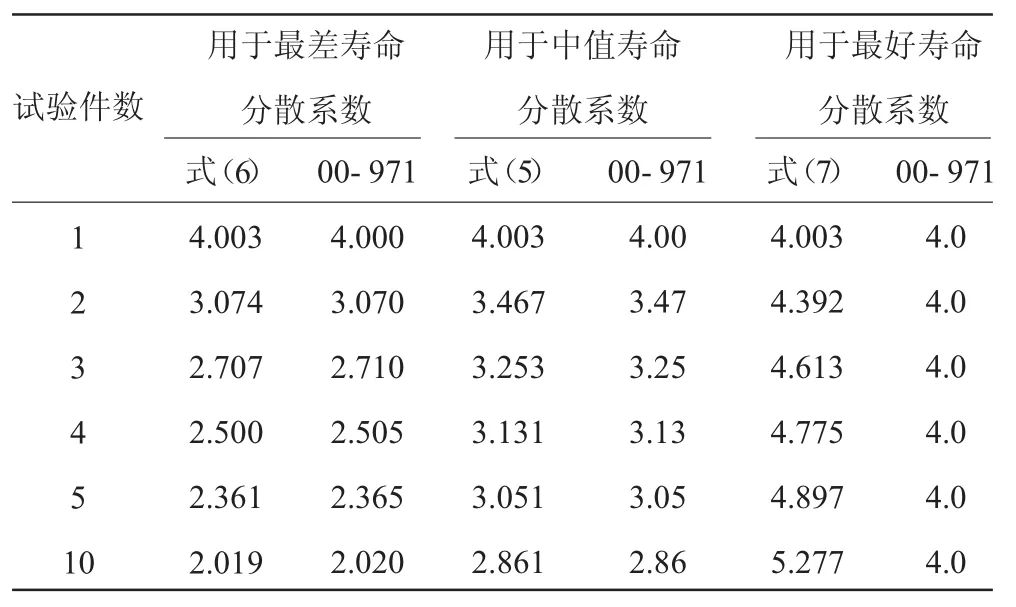
表1 服從對(duì)數(shù)正態(tài)分布的發(fā)動(dòng)機(jī)輪盤裂紋形成壽命分散系數(shù)γ=95%,p=99.87%,σ0=0.13
文獻(xiàn)[5]推導(dǎo)了壽命服從對(duì)數(shù)正態(tài)分布,假設(shè)可靠度p=99.87%、置信度γ=95%,對(duì)數(shù)壽命標(biāo)準(zhǔn)差σ0=0.13。基于n個(gè)子樣中任意第k次試驗(yàn)壽命的分散系數(shù)。
(4)基于第k試驗(yàn)壽命N(k)的分散系數(shù)

式中:F(μ)是母體的概率分布函數(shù),子樣第k次序統(tǒng)計(jì)量的概率分布F(k)(μ)可用該函數(shù)表示。具體推導(dǎo)過程見文獻(xiàn)[5]。
通過式(8)可得任意給定置信度、可靠度和子樣數(shù)n的基于任意第k試驗(yàn)壽命的分散系數(shù)。當(dāng)k=1或者k=n時(shí),式(8)分別為零故障和完全故障試驗(yàn)壽命分散系數(shù)計(jì)算公式。
3.1.2 基于對(duì)數(shù)正態(tài)分布分散系數(shù)標(biāo)準(zhǔn)差的確定
對(duì)于對(duì)數(shù)正態(tài)分布最為重要的是確定母體對(duì)數(shù)壽命標(biāo)準(zhǔn)差。可由以下幾種方法確定:
(1)根據(jù)大量的真盤試驗(yàn)值確定。
(2)根據(jù)試樣低循環(huán)疲勞性能數(shù)據(jù)統(tǒng)計(jì)確定[7]。
(3)數(shù)值模擬方法獲得構(gòu)件危險(xiǎn)部位壽命N0.13、N99.87,對(duì)數(shù)正態(tài)分布母體標(biāo)準(zhǔn)差為 σ0=(log(N0.13/N99.97))/6。
方法(1)最為直接,而且最接近母體真實(shí)方差。但由于輪盤造價(jià)昂貴,試驗(yàn)成本高,只能采用極小子樣壽命試驗(yàn),很難獲得大量真盤壽命試驗(yàn)數(shù)據(jù);方法(2)成本不高,但隨著樣本數(shù)量的不同,標(biāo)準(zhǔn)差估計(jì)值相差較大;方法(3)采用蒙特卡羅法或面響應(yīng)面法擬合出輪盤考核點(diǎn)壽命概率密度曲線,通過概率密度曲線得到母體標(biāo)準(zhǔn)差[12-13]。數(shù)值模擬為理論計(jì)算,與實(shí)際試驗(yàn)值有誤差。該方法主要用于輪盤可靠性數(shù)值模擬分析,在試驗(yàn)評(píng)估中一般不采用。
對(duì)于標(biāo)準(zhǔn)差的選擇,各國(guó)有較大差別,見表2。在飛機(jī)方面,美國(guó)取0.2,澳大利亞、英國(guó)和中國(guó)取0.176,日本取0.154。中國(guó)在飛機(jī)結(jié)構(gòu)壽命的可靠性估算中采用文獻(xiàn)[7]中給出的計(jì)算公式及各類安全標(biāo)準(zhǔn)差值。而在發(fā)動(dòng)機(jī)輪盤方面,英國(guó)通過大量的真盤試驗(yàn)和長(zhǎng)期的經(jīng)驗(yàn)取0.13,中國(guó)目前也參照該值計(jì)算。
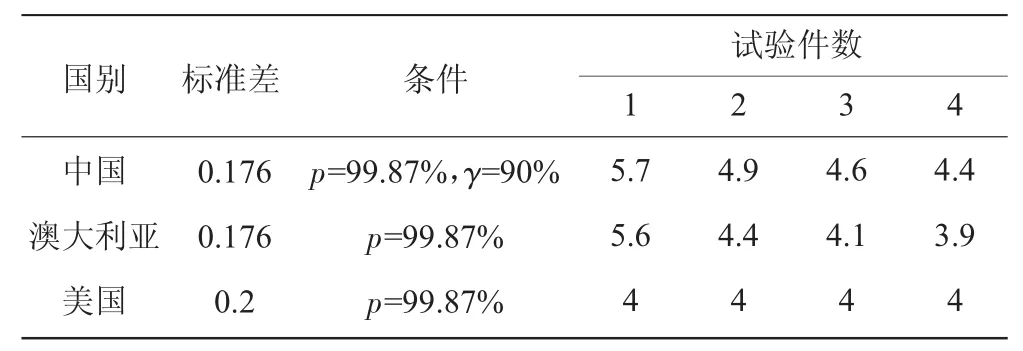
表2 各國(guó)服從對(duì)數(shù)正態(tài)分布裂紋形成壽命分散系數(shù)(飛機(jī)結(jié)構(gòu)可靠性)
3.2 基于威布爾分布的分散系數(shù)
威布爾分布是疲勞強(qiáng)度研究中的1種常用分布。其最大優(yōu)點(diǎn)是存在最小安全壽命,即100%存活率的安全壽命。而正態(tài)分布安全壽命為0時(shí),存活率才能等于100%。所以威布爾分布更符合工程實(shí)際,其分布函數(shù)為
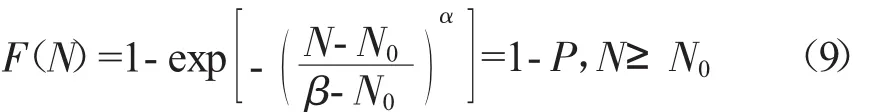
式中:α為形狀參數(shù),一般α>1;β為特征壽命;N0為最小壽命,也稱位置參數(shù)。當(dāng)N0>0時(shí),稱為3參數(shù)威布爾分布;當(dāng)N0=0時(shí),稱為雙參數(shù)威布爾分布。目前研究較多的是基于雙參數(shù)威布爾分布的分散系數(shù),而基于3參數(shù)威布爾分布的分散系數(shù),由于影響分散系數(shù)的參數(shù)較多,而且影響程度不同,研究得較少。
3.2.1 基于雙參數(shù)威布爾分布的分散系數(shù)
美國(guó)《航空渦噴渦扇渦軸渦槳發(fā)動(dòng)機(jī)通用規(guī)范》(JSGS-87231A)假設(shè)疲勞壽命服從雙參數(shù)威布爾分布,給出了1個(gè)確定渦輪盤試驗(yàn)時(shí)間的簡(jiǎn)單算例。文獻(xiàn)[9]假設(shè)疲勞壽命服從雙參數(shù)威布爾分布,給出了利用小子樣基于中值、最差和最好壽命分散系數(shù)試驗(yàn)壽命的分散系數(shù)計(jì)算公式,并應(yīng)用該公式評(píng)估了某風(fēng)扇輪盤的安全壽命。
基于最差、中值和最好壽命的分散系數(shù)分別為
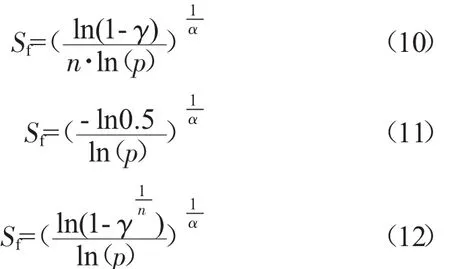
從式(11)中可見,基于中值壽命的分散系數(shù)是理論值,與試驗(yàn)次數(shù)無(wú)關(guān)。而考慮置信度后,基于中值壽命的分散系數(shù)為
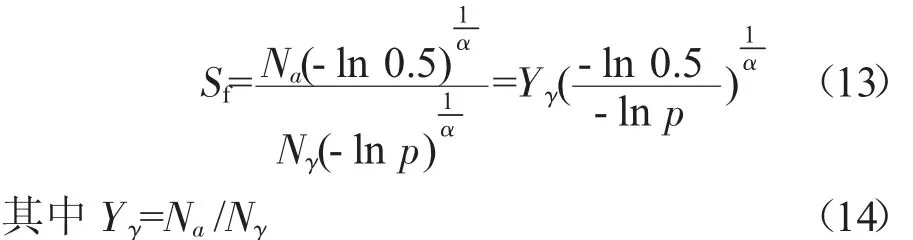
式中:Na為根據(jù)試件的疲勞試驗(yàn)值由極大似然法估計(jì)得到的特征壽命的估計(jì)值;Nγ為Na的單側(cè)置信下限。
基于第k試驗(yàn)壽命N(k)的分散系數(shù)公式為

式中:yγ為任意第k次序統(tǒng)計(jì)量的分布函數(shù)在子樣數(shù)n、故障數(shù)k-1、以及在雙參數(shù)威布爾分布和模型參數(shù)已知的情況下在0-1區(qū)間的根。
在已知置信度、破壞數(shù)、可靠度、試驗(yàn)截止時(shí)間及部件數(shù)的情況下,該方法可確定可靠壽命,還可反推產(chǎn)品試件數(shù)或者破壞數(shù)。
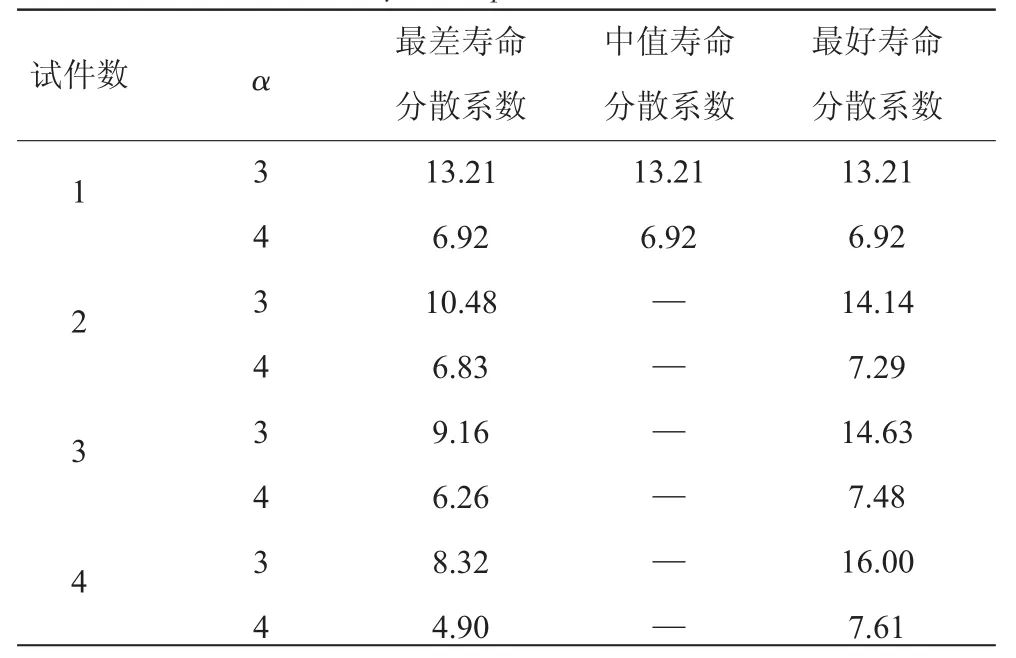
表3 服從威布爾分布的裂紋形成壽命分散系數(shù)(γ=95%,p=99.87%)
3.2.2 基于雙參數(shù)威布爾分布形狀參數(shù)的確定
根據(jù)表3和文獻(xiàn)[3],對(duì)比不同形狀參數(shù)的分散系數(shù)可知:服從雙參數(shù)威布爾分布的小子樣疲勞壽命分散系數(shù)對(duì)形狀參數(shù)α的變化比較敏感。對(duì)服從威布爾分布?jí)勖稚⑾禂?shù)的研究主要是對(duì)分布參數(shù)α進(jìn)行估計(jì)。α與分散性有關(guān),α越小分散性越大,反之亦然。目前國(guó)內(nèi)使用的疲勞分布參數(shù)α主要是由《實(shí)用飛機(jī)結(jié)構(gòu)設(shè)計(jì)手冊(cè)》給出的估計(jì)值:α=4,適用于鋁結(jié)構(gòu)(所有合金);α=3,適用于鈦合金和熱處理σb≤1700 MPa 的鋼;α=2.2,適用于熱處理 σb>1700 MPa的鋼。
周希沅在文獻(xiàn)[8]中根據(jù)國(guó)產(chǎn)材料及小結(jié)構(gòu)件的疲勞試驗(yàn)數(shù)據(jù),估計(jì)出威布爾分布的形狀參數(shù)α,并與美國(guó)材料α進(jìn)行比較,認(rèn)為國(guó)產(chǎn)材料的α和疲勞壽命的分散性均與美國(guó)材料的相當(dāng)。但仍然推薦使用《實(shí)用飛機(jī)結(jié)構(gòu)設(shè)計(jì)手冊(cè)》中的α值。而對(duì)用于航空發(fā)動(dòng)機(jī)高溫合金的α值,還沒有相關(guān)的研究,通常值介于3~4之間[12],在美國(guó)JSGS-87231A中α取3。
3.3 同應(yīng)力多危險(xiǎn)部位分散系數(shù)
航空發(fā)動(dòng)機(jī)輪盤低循環(huán)疲勞危險(xiǎn)部位一般是多個(gè),而且具有相同的結(jié)構(gòu)、應(yīng)力和溫度。危險(xiǎn)部位數(shù)目對(duì)低循環(huán)疲勞壽命影響屬于尺寸效應(yīng)的研究范疇。文獻(xiàn)[3]將多危險(xiǎn)部位按照最弱環(huán)理論將其等效為1個(gè)可靠性串連系統(tǒng)。即認(rèn)為n個(gè)危險(xiǎn)部位中有任何1個(gè)部位出現(xiàn)疲勞失效,就認(rèn)為輪盤發(fā)生失效。實(shí)際上有些片面,沒有考慮各危險(xiǎn)部位的相關(guān)性,估計(jì)出的輪盤壽命往往過于保守。而陸山教授[12]考慮了各危險(xiǎn)部位的相關(guān)性,認(rèn)為由于輪盤具有同樣應(yīng)力水平的危險(xiǎn)部位通常有多個(gè),并且各孔的壽命分散程度與母體壽命分散程度有差異,直接采用00-971提供的壽命分散系數(shù)進(jìn)行試驗(yàn)壽命評(píng)估偏保守,提出采用區(qū)間估計(jì)分散系數(shù)法和均值分散系數(shù)法2種方法進(jìn)行輪盤低循環(huán)疲勞壽命試驗(yàn)評(píng)估。目前,國(guó)內(nèi)在這方面的研究還很有限。
3.4 疲勞壽命分散系數(shù)隨應(yīng)力的變化規(guī)律
很多研究是針對(duì)材料質(zhì)量、制造工藝、試件幾何尺寸、計(jì)算模型等方面對(duì)疲勞壽命分散系數(shù)的影響進(jìn)行的。而張福澤院士[10]對(duì)載荷大小與疲勞壽命分散系數(shù)之間關(guān)系進(jìn)行了研究,通過267個(gè)鋁合金試件和139個(gè)鋼合金試件的疲勞試驗(yàn)數(shù)據(jù),繪出疲勞壽命分散系數(shù)Sf與試驗(yàn)最大應(yīng)力σmax之間的關(guān)系曲線,并得出疲勞壽命分散系數(shù)隨應(yīng)力的提高而減小的規(guī)律。
對(duì)于輪盤來(lái)說,工作過程中某型局部區(qū)域已進(jìn)入塑性變形狀態(tài),輪盤的壽命由該處的應(yīng)變幅值決定,故而該處的應(yīng)變幅值顯得更為重要,研究應(yīng)變幅值與散度系數(shù)的關(guān)系對(duì)于輪盤的技術(shù)壽命研究意義很大。
文獻(xiàn)[10]都是針對(duì)飛機(jī)材料,如鋁合金、鋼合金等進(jìn)行研究的,而航空發(fā)動(dòng)機(jī)渦輪盤主要材料為高溫合金,目前對(duì)其疲勞壽命分散系數(shù)研究較少。除了文獻(xiàn)[5]給出的分散系數(shù)表,還可以通過盤材試件的低循環(huán)疲勞性能數(shù)據(jù)統(tǒng)計(jì)后得到。文獻(xiàn)[14]就做過這方面的研究,通過不同溫度、應(yīng)變比或應(yīng)力比的疲勞性能數(shù)據(jù)統(tǒng)計(jì)值確定出相應(yīng)的疲勞壽命分散系數(shù),最后采用某溫度下缺口試樣的子樣標(biāo)準(zhǔn)差和真盤的標(biāo)準(zhǔn)差的均值來(lái)得到最終的標(biāo)準(zhǔn)差,進(jìn)而得到分散系數(shù)。由于航空發(fā)動(dòng)機(jī)輪盤在工作過程中所承受的溫度、應(yīng)力和應(yīng)變都是不同的,故而一定要在相應(yīng)的載荷狀態(tài)下確定發(fā)動(dòng)機(jī)輪盤的分散系數(shù)。
4 輪盤疲勞安全循環(huán)壽命的確定
4.1 第Ⅰ級(jí)高壓渦輪盤低循環(huán)疲勞試驗(yàn)[14]
對(duì)某型發(fā)動(dòng)機(jī)第Ⅰ級(jí)高壓渦輪盤進(jìn)行低循環(huán)疲勞試驗(yàn),在輪盤多個(gè)銷釘孔出現(xiàn)明顯可見裂紋時(shí)結(jié)束。分別對(duì)3個(gè)試驗(yàn)盤進(jìn)行疲勞壽命試驗(yàn),其壽命循環(huán)數(shù)分別為 1#:4670;2#:3820;3#:4350;平均壽命循環(huán)數(shù)為4280。從表1中得到壽命分散系數(shù)Y=3.25(可靠度p=99.87%、置信度γ=95%,對(duì)數(shù)壽命方差σ=0.13),計(jì)算得出安全循環(huán)壽命為1336個(gè)標(biāo)準(zhǔn)循環(huán)。第Ⅰ級(jí)高壓渦輪盤試驗(yàn)件裝配關(guān)系如圖1所示;試驗(yàn)第I級(jí)高壓渦輪盤在試驗(yàn)器上的安裝方案如圖2所示。
4.2 第Ⅱ級(jí)高壓渦輪盤低循環(huán)疲勞試驗(yàn)[18]
對(duì)某型發(fā)動(dòng)機(jī)第Ⅱ級(jí)高壓渦輪盤進(jìn)行低循環(huán)疲勞試驗(yàn),由于渦輪盤的中心孔出現(xiàn)裂紋,擴(kuò)展速率較快,可能導(dǎo)致盤破裂發(fā)生危險(xiǎn)性故障,而傳動(dòng)臂銷釘孔裂紋的影響可能不大(根據(jù)具體試驗(yàn)裂紋萌生壽命、擴(kuò)展速率、方向確定)。所以,如果中心孔未出現(xiàn)裂紋時(shí),傳動(dòng)臂銷釘孔已出現(xiàn)裂紋,只要裂紋局限在傳動(dòng)臂安裝邊,未通過傳動(dòng)臂向輪盤本體擴(kuò)展,則繼續(xù)試驗(yàn);若發(fā)現(xiàn)裂紋已通過傳動(dòng)臂向輪盤本體擴(kuò)展,則終止試驗(yàn)。傳動(dòng)臂試驗(yàn)壽命按此時(shí)的循環(huán)數(shù)確定,最后得到該渦輪盤試驗(yàn)循環(huán)數(shù)為5000循環(huán)。第Ⅱ級(jí)渦輪盤試驗(yàn)裝配關(guān)系如圖3所示;試驗(yàn)第Ⅱ級(jí)高壓渦輪盤在試驗(yàn)器上的安裝方案如圖4所示。
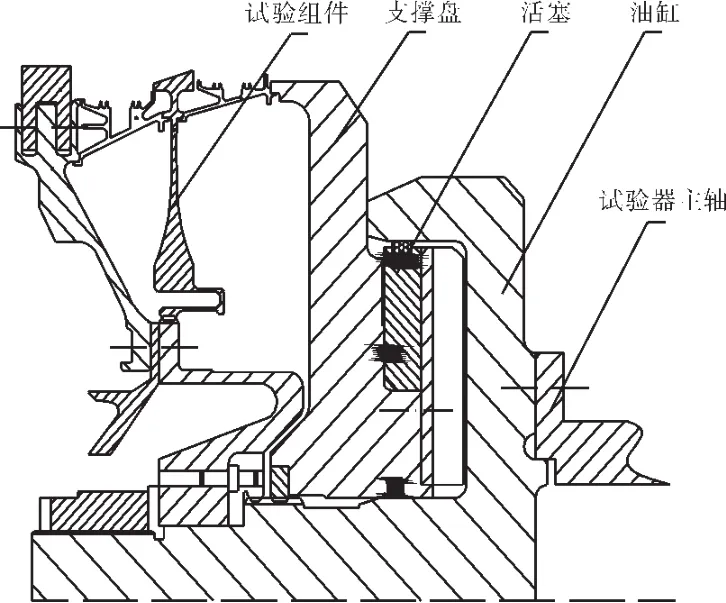
圖1 第I級(jí)高壓渦輪盤試驗(yàn)件裝配關(guān)系

圖2 試驗(yàn)第I級(jí)高壓渦輪盤在試驗(yàn)器上的安裝方案
根據(jù)表1的處理方法,當(dāng)只有1個(gè)試驗(yàn)結(jié)果時(shí),壽命散度系數(shù)為4。但考慮到銷釘孔處應(yīng)力較高,疲勞壽命分散度小,壽命分散系數(shù)取4不是很合理。傳動(dòng)臂銷釘孔共有16個(gè),按照銷釘孔裂紋擴(kuò)展到盤轉(zhuǎn)接R處作為發(fā)生故障,符合基于正態(tài)分布任意第k個(gè)試驗(yàn)壽命次序來(lái)確定散度系數(shù)[14],根據(jù)試驗(yàn)結(jié)果,有3個(gè)銷釘孔裂紋擴(kuò)展到盤轉(zhuǎn)接R處。故而得到16個(gè)樣本的第4個(gè)壽命次序量的散度系數(shù)為2.2972[5](可靠度p=99.87%、置信度γ=95%,對(duì)數(shù)壽命方差σ=0.13),由該分散系數(shù)得到的預(yù)定安全循環(huán)數(shù)為第Ι級(jí)高壓渦輪盤2531循環(huán),第Ⅱ級(jí)高壓渦輪盤2354循環(huán)。其他相關(guān)研究還可參見文獻(xiàn)[16-17]。
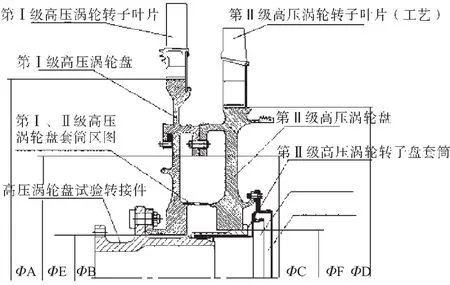
圖3 第Ⅱ級(jí)高壓渦輪盤試驗(yàn)裝配關(guān)系

圖4 試驗(yàn)第Ⅱ級(jí)高壓渦輪盤在試驗(yàn)器上的安裝方案
5 展望
綜上所述,根據(jù)國(guó)內(nèi)外對(duì)疲勞壽命分散系數(shù)研究的進(jìn)展,確定進(jìn)一步的研究工作。
(1)對(duì)于航空發(fā)動(dòng)機(jī)輪盤用高溫合金,由于不同溫度下和應(yīng)變狀態(tài)下疲勞分散性差別很大,應(yīng)開展對(duì)其分散系數(shù)的研究。
(2)對(duì)于服從對(duì)數(shù)正態(tài)分布的分散系數(shù)研究,應(yīng)不斷積累高溫合金的疲勞試驗(yàn)結(jié)果和真盤試驗(yàn)結(jié)果,經(jīng)過統(tǒng)計(jì)得到符合中國(guó)實(shí)際情況的標(biāo)準(zhǔn)差σ0。
(3)由于航空發(fā)動(dòng)機(jī)輪盤通常有多個(gè)具有相同的結(jié)構(gòu)、應(yīng)力和溫度的部位,同應(yīng)力多危險(xiǎn)部位分散系數(shù)有待進(jìn)一步研究。
(4)壽命服從3參數(shù)的威布爾分布的疲勞壽命分散系數(shù)研究較少,可做進(jìn)一步研究。
(5)進(jìn)一步開展疲勞分散系數(shù)的工程化應(yīng)用研究。
[1]高鎮(zhèn)同.疲勞應(yīng)用統(tǒng)計(jì)學(xué)[M].北京:國(guó)防工業(yè)出版社,1986:375-381.GAO Zhentong.The fatigue of applied statistics[M].Beijing:National Defence Industry Press,1986:375-381.(in Chinese)
[2]宋兆泓,付小平,吳樹雄.某渦輪盤小子樣低周疲勞壽命評(píng)估計(jì)算——威伯斯先驗(yàn)評(píng)估法[J].航空發(fā)動(dòng)機(jī),2002(3):18-20.SONG Zhaohong,F(xiàn)U Xiaoping,WU Shuxiong.Prediction of low cycle fatigue life for turbine disk by small sample——webayes method[J].Aeroengine,2002(3):18-20.(in Chinese)
[3]王衛(wèi)國(guó).輪盤低循環(huán)疲勞壽命預(yù)測(cè)模型和試驗(yàn)評(píng)估方法研究[D].南京:南京航空航天大學(xué),2006.WANG Weiguo.Research on prediction model for disc LCF life and experiment assessment methodology[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2006.(in Chinese)
[4]張福澤.疲勞分散系數(shù)的分類及其取值 [J].航空學(xué)報(bào),1987,8(6):B239-B243.ZHANG Fuze.The categories and values of fatigue scatter factors[J].Acta Aeronautica et Astronautica Sinica,1987,8 (6):B239-B243.(in Chinese)
[5]盧小艷,陸山.基于對(duì)數(shù)正態(tài)分布第k試驗(yàn)壽命的分散系數(shù)法[J].航空動(dòng)力學(xué)報(bào),2006,21(4):738-740.LU Xiaoyan,LU Shan.Life scatter factor method based on the kth order experimental life with logarithm normal distribution[J].Journal of Aerospace Power,2006,21(4):738-740.(in Chinese)
[6]賀小帆,劉文廷.服從不同分布的疲勞壽命分散系數(shù)分析[J].北京航空航天大學(xué)學(xué)報(bào),2002,28(1):47-49.HE Xiaofan,LIU Wenting.On scatter factors of fatigue life obeying different distributions[J].Journal of Beihang University,2002,28(1):47-49.(in Chinese)
[7]張福澤.疲勞分散系數(shù)中標(biāo)準(zhǔn)差的研究 [J],航空學(xué)報(bào),1986(1):25-28.ZHANG Fuze.The research of standard deviation of the fatigue scatter factor[J].Acta Aeronautica et Astronautica Sinica,1986(1):25-28.(in Chinese)
[8]周希沅.國(guó)產(chǎn)材料疲勞壽命分布參數(shù)的初步估計(jì) [J].航空學(xué)報(bào),1990,11(10):488-491.ZHOU Xiyuan.Preliminary estimation of the shape parameters of fatigue life distribution for homemade materials.[J].Acta Aeronautica et Astronautica Sinica,1990,11(10):488-491.(in Chinese)
[9]陸山,唐俊星.同應(yīng)力多危險(xiǎn)部位輪盤壽命可靠性試驗(yàn)評(píng)估方法[J].燃?xì)鉁u輪試驗(yàn)與研究,2007,20(2):5-8.LU Shan,TANG Junxing.Experimental assessment method of life reliability of a disk with multi-samestress critical sites[J].Gas Turbine Experiment and Research,2007,20(2):5-8.(in Chinese)
[10]張福澤.疲勞分散系數(shù)隨應(yīng)力的變化規(guī)律 [J].航空學(xué)報(bào),2007,28(3):582-585.ZHANG Fuze.Law of fatigue scatter factor versus test stress[J].Acta Aeronautica et Astronautica Sinica,2007,28 (3):582-585.(in Chinese)
[11]陸山,楊劍秋.基于小子樣最差和最好試驗(yàn)結(jié)果的壽命分散系數(shù)法[J].機(jī)械科學(xué)與技術(shù),2006,25(1):99-101.LU Shan,YANG Jianqiu.Life scatter factor method based on the worst and the best experiment results of small samples[J].Mechanical Science and Technology,2006,25(1):99-101.(in Chinese)
[12]唐俊星,陸山.某渦輪盤低循環(huán)疲勞概率壽命數(shù)值模擬[J].航空動(dòng)力學(xué)報(bào),2006,26(4):706-710.TANG Junxing,LU Shan.Numerical simulation of LCF probability life of a turbine disk[J].Journal of Aerospace Power,2006,26(4):706-710.(in Chinese)
[13]李斌,白廣忱.某飛行科目中渦輪盤的損傷計(jì)算[J].航空發(fā)動(dòng)機(jī),2013,39(5):55-59.LI Bin,BAIGuangchen.Damage calculation of turbine disk in a flight subject[J].Aeroengine,2013,39(5):55-59.(in Chinese)
[14]楊俊,謝壽生,祁圣英.基于等效應(yīng)變的輪盤低循環(huán)疲勞壽命預(yù)測(cè)[J].空軍工程大學(xué)學(xué)報(bào)(自然科學(xué)版),2010,11(6):12-16.YANG Jun,XIE Shousheng,QI Shengying.Disk low cycle fatigue life prediction based on equivalent strain [J].Journal of Air Force Engineering University(Natural Science Edition).2010,11(6):12-16.(in Chinese)
[15]楊俊,張貴斌,祁圣英.發(fā)動(dòng)機(jī)高壓兩級(jí)渦輪盤聯(lián)合低循環(huán)疲勞壽命試驗(yàn)[J].燃?xì)鉁u輪研究與試驗(yàn),2012,25(1):9-13.YNAG Jun,ZHANG Guibin,QI Shengying.Joint test of two-stage HP turbine disk low cycle fatigue life[J].Gas Turbine Experiment and Research,2012,25(1):9-13.(in Chinese)
[16]蔚奪魁,邵丕仁.某型發(fā)動(dòng)機(jī)渦輪盤銷釘孔邊低循環(huán)疲勞壽命分析[J].航空發(fā)動(dòng)機(jī),2000(2):37-41.YU Duokui,SHAO Peiren.Low cycle fatigue life analysis of turbine disk pin holes in aeroengine[J].Aeroengine,2000 (2):37-41.(in Chinese)
[17]葉大榮.某型發(fā)動(dòng)機(jī)渦輪盤強(qiáng)度與疲勞壽命計(jì)算[J].航空發(fā)動(dòng)機(jī),2006,32(4):16-18.YE Darong.Strength and fatigue life calculation of an engine turbine disk[J].Aeroengine,2006,32(4):16-18.(in Chinese)
Determination and Application of Fatigue Scatter Factors
YANG Jun,WANG Jian,QI Sheng-ying
(A Military Representative Office,Airforce Xi'an Bureau,Xi'an 710021,China)
Fatigue life scatter factor is one of the key technical parameters for aircraft parts fatigue life and aeroengine disk life experimental assessment.The development of fatigue life scatter factors was reviewed.Aiming at the logarithm-normal distribution and the Weibull distribution commonly used in engineering,the theoretical formulas of the life scatter factor based on the worst,median and the best experimental lives were given.A particular focus was placed on the analysis of selecting of the standard deviation of logarithm-normal distribution and the shape parameters of Weibull distribution,and on the research of scatter factor of multi same-stress critical sites,the law of scatter factor versus test stress.Two examples illustrated the engineering application of life scatter factor determination in disk low cycle fatigue.The results show that the fatigue life scatter factor investigation in combine with the future research focus on the areas such as different temperature and strain,standard deviation of logarithm-normal distribution,multisame-stresscritical sites,three parameter Weibull distribution,and engineering application should be conducted.
fatigue life;scatter factor;logarithm-normal distribution;Weibull distribution;disk;aeroengine;aircraft
V231.91
A
10.13477/j.cnki.aeroengine.2015.01.003
2014-02-22
楊俊(1979),男,博士,研究方向?yàn)楹娇瞻l(fā)動(dòng)機(jī)強(qiáng)度、壽命和可靠性;E-mail:yangjunkgy_013@163.com。
楊俊,王建,祁圣英.疲勞壽命分散系數(shù)的確定與應(yīng)用研究[J].航空發(fā)動(dòng)機(jī),2015,41(1):16-21.YANGJun,WANGJian,QIShengying.Determination and application of fatiguelifescatter factors[J].Aeroengine,2015,41(1):16-21.
(編輯:肖磊)

