航空發動機部件特性修正技術研究

賈忠湖，郭衛剛，馬 力

航空發動機部件特性修正技術研究

賈忠湖1，郭衛剛1，馬 力2

（1.海軍航空工程學院飛行器工程系，山東煙臺264001；2.海軍駐沈陽地區發動機專業軍事代表室，沈陽110043）

針對傳統部件特性修正方法未考慮發動機多狀態導致修正精度不高的問題，提出了1種基于粒子群優化和滑動最小二乘法的某型發動機部件特性修正方法。該方法利用粒子群優化算法分別求得在發動機不同狀態下的修正系數，并以這些系數為基礎，采用滑動最小二乘方法擬合修正系數曲面，從系數曲面上獲取原有部件特性圖上各點對應的修正系數，從而得到修正特性。試驗結果表明：該方法克服了傳統方法的不足，提高了特性修正精度，為開展單機監控和視情維修提供準確的部件數據基礎。

部件特性修正;粒子群算法;滑動最小二乘法;航空發動機

0 引言

不同型號的發動機有著不同的特性，甚至同一類型、同一批次的發動機由于制造和安裝工藝的差異，其部件特性也會有所差異，使得每臺發動機的性能不完全相同。因此，發動機模型的仿真結果與其真實性能存在一定誤差。因此，有必要針對單臺發動機的性能對模型進行修正，使模型能夠與真實發動機匹配[1-5]。

國內外專家提出了一些針對發動機部件特性的修正方法。文獻[6]提出了經典的修正因子法，可根據試驗數據，采用優化算法求出；文獻[7]發展了1種預測發動機部件特性的自適應模型方法；文獻[8]分析了部件特性自適應模型的不足，利用“部件特性刪除法”求解修正因子。

經典的修正因子法最大的改進是不再視修正因子為定值，而是隨狀態變化而變化。基于這樣的思路，本文提出1種更加有效地綜合利用航空發動機多個狀態試車數據的修正方法。

1 部件級穩態發動機模型的建立

發動機部件級解析模型建立的基本步驟和思路見文獻[9-10]，采用變比熱技術建立該型發動機各部件的氣動熱力模型。整臺發動機在非設計點工作時各部件狀態是互相制約的，即需滿足共同工作條件。共同工作條件包括：流量平衡、功率平衡、靜壓平衡和轉速平衡。穩態工作點求解的基本思路是對從進氣道入口至尾噴管出口截面所建的部件模型進行計算，遇到未知量就假定為已知，稱為獨立變量，按氣流流過的順序，完成所有部件氣動熱力計算，從而得到表示發動機工作的6個方程，稱為發動機共同工作方程。根據該型發動機的調節規律確定出的6個待求獨立變量為：風扇工作點位置參數βcL、高壓轉速nH、壓氣機工作點位置參數βcH、燃燒室出口總溫、高壓渦輪單位焓降和低壓渦輪單位焓降。則共同工作方程組為

式（1）表示的共同工作方程是包含獨立變量為未知數的6個隱式非線性方程，穩態工作點求解的數學問題即為求解以獨立變量為未知數的非線性隱式方程組。要獲得共同工作方程需進行1次完整的發動機氣動熱力計算，因此，該非線性方程組是非常復雜的。簡而言之，求解發動機部件級模型的數學問題就是求解1個復雜的多維非線性隱式方程組。

2 基于粒子群優化的方程求解

從上節分析可知，部件特性修正本質上是1個非線性方程組的優化過程。對這類問題的優化求解可采用傳統的迭代法，但存在受初值影響較大，不易收斂等不足[11]。并且隨著目標方程數目增加，求解變得更加困難；粒子群算法是近年來提出的群智能優化算法，適合解決復雜的非線性優化問題。因此，采用粒子群算法對共同工作方程組進行求解。

粒子群優化算法是1種模擬鳥群覓食過程中遷徙和聚集行為的進化算法[12-13]。假設在1個n維的目標搜索空間中，有N個粒子組成1個群體，其中第i個粒子表示 1 個 n 維的向量 xi=（xi1，xi2，…，xin），i=1，2，…，N，則每個粒子的位置就是1個潛在的解。第i個粒子的飛行速度也是1個n維向量，記為Vi=（Vi1,Vi2，…，Vin），記第i個粒子迄今為止搜索到的最優位置為 Pi=（Pi1,Pi2，…，Pin），整個粒子群迄今為止搜索到的最優位置為 Pg=（Pg1,Pg2，…，Pgn），w 為慣性權重。在每一步迭代中，粒子可根據以下公式更新自己的速度和位置

因子c1和c2分別用來調節該粒子向自身已經歷過的最優位置和同伴已尋找到的最優位置方向飛行的最大步長。增大c1和c2可使粒子向全局及個體最優位置飛行的速度加快，從而加快收斂速度，但過大的c1和c2可能導致由于飛行速度過快而飛過目標區域，選擇合適的c1和c2可以加快收斂速度又能避免陷入局部最優，通常情況下取c1=c2=2。隨機數r1和r2使得粒子飛行時的速度具有了一定的隨機性，這種隨機性提高了粒子在解空間的搜索能力。較小的慣性權重w可加強粒子局部搜索能力，而較大的w可加快收斂速度，所以可通過調節w來兼顧收斂速度和收斂精度，w常在[0.4，0.9]之間變化，隨著迭代步數的增加而減小，使得早期具有較快的收斂速度，而后期又有較強的局部搜索能力。根據具體問題，當飛行速度足夠小或達到預設的迭代步數時，停止迭代，輸出最優解。

式（1）表示的共同工作方程組的求解過程可轉化為如下優化問題進行尋優求解

對于上述優化問題，利用粒子群算法進行求解，粒子 xi=（xi1，xi2，…，xi12），各維度分別對應 βcL，nH，βcH，適應度函數選取為

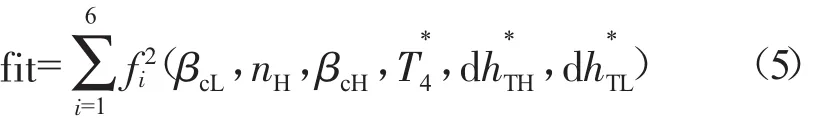
3 基于滑動最小二乘法的部件特性修正

利用該型發動機多個工作狀態下的試車數據，以風扇部件為例進行多狀態部件特性修正。粒子群算法求解部件特性修正系數得到在已知7個狀態下的風扇增壓比修正系數，比較發現在不同工作范圍得到的修正系數也不同。因此,傳統方法對于整個范圍的部件特性取相同的修正系數值是不準確的。通過計算可以得到風扇部件在較大范圍內多個狀態的增壓比修正系數，但受試驗所限，不可能對所有狀態進行試驗。因此,對于已知狀態之間的任意狀態，其修正系數可以根據該狀態周圍的已知狀態特性求取。如果利用所有已知狀態點的修正系數，能夠擬合出1個系數曲面，則任意狀態的修正系數可從該曲面獲得。

近年來滑動最小二乘（MLS，Moving Least Square）在曲面擬合方面取得較好的效果[14-15]，本文即采用滑動最小二乘法進行曲面擬合。滑動最小二乘法是1種基于點的近似方法，具有擬合精度高，通用性強的特點。其擬合函數采用隨坐標變化的系數向量來代替傳統最小二乘法的固定系數，因此，不存在對復雜、離散數據量的分段（分塊）擬合和平滑化等問題，解決了傳統曲線曲面擬合過程中存在的困難。

假設計算區域內擬合函數為

式中：x，y，z為計算區域的坐標變量。

設在n個結點zi=（xi，y）i有已知的實測值，分別為σi=σ（xi，y）i，i=1，2，…，n。用矢量形式可表示為

設擬合函數可近似表示為

式中：b1（z）為m個線性無關的基函數，且b1=1；bT（z）為由這些基函數組成的m維函數矢量；λ（z）為m維系數矢量，待求。

與經典的擬合方法不同，這里的待定系數λ（z）是隨著域內變量z變化的。首先固定1點z^，稱為估值點。研究在這點鄰域內的局部近似

所要求的近似函數與真實函數在已知的n個實測點上的加權平方范數最小，即

其中

由于基函數bi（z）已知，則測值點場坐標zi已知，因此，矩陣B是由確定數值元素構成的。權矩陣W是對角矩陣，其元素Wi（z^-zi）是非負的可導函數。為減少計算量，結點權函數只在其影響區域B（zi）內非零，即

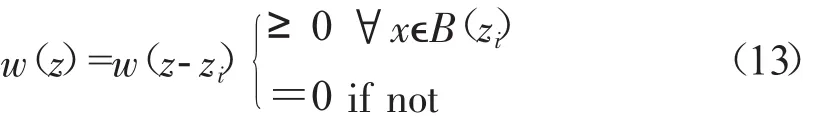
可解出

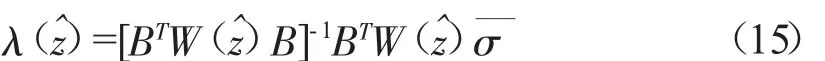
將式（14）代到式（9），得到在估值點（z^）附近的近似函數

對每個估值點z^必須確定1個相應的系數矢量λ（z^），這是因為權矩陣在數值上隨估值點的不同而變化。現在使量z^成為計算區域內的任意1點，即z^可用z代替，則得到全局滑動最小二乘法的近似函數

如果W（z）是常數矩陣，式（17）是1個經典的、非活動的、加權最小二乘法的近似函數。由于權函數是非線性函數，該式不能表述為1個解析函數，只能用數值方法求解。

權函數采取以下形式

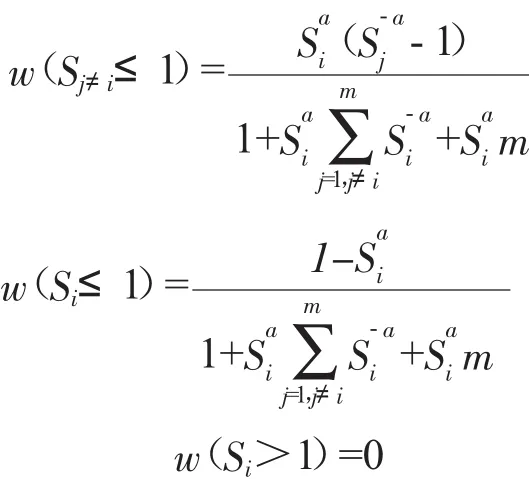
式中：m為影響區域內包含的結點個數；Si為與估值點距離最近的結點距離；Sj≠i為影響區域內其它結點與估值點的距離。

4 試驗分析

利用MLS和已知的修正系數點擬合計算獲得風扇的增壓比修正系數曲面，如圖1所示（圖中曲面只畫出風扇特性覆蓋的范圍）。用同樣方法獲得風扇的流量特性修正系數曲面，如圖2所示。

利用得到的相應修正系數曲面，可以獲得精確的修正特性圖。以風扇增壓比特性為例，對于任何1個轉速線上的點（每個轉速線上有10個點），則依據其在原來特性圖上的坐標，對應到2個修正系數曲面上，找到平面上相應位置對應到特性曲面的z軸值即為該點的修正系數。利用所求的原特性圖上所有點的修正系數計算出修正后的風扇增壓比和效率。修正前、后的風扇增壓比和效率特性分別如圖3、4所示。

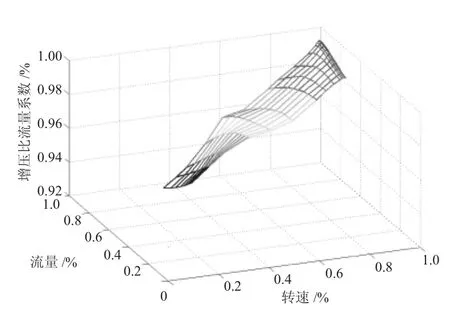
圖1 風扇的增壓比修正系數曲面

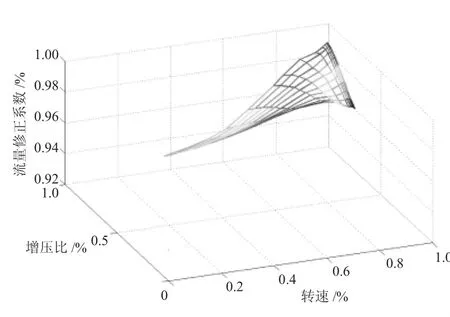
圖2 風扇的流量修正系數曲面

圖3 修正前、后的風扇增壓比特性

為了驗證本文方法得到修正特性的精度，分別利用經典方法、曲線擬合方法和本文方法得到修正部件特性，進行發動機穩態性能仿真計算。3種方法的發動機模型非線性方程組均采用粒子群算法求解，算法均迭代運算100次，并取相同的參數設置。以某渦扇發動機2個不同的狀態I、II來驗證由不同方法獲得部件特性的精度，2個狀態的對應的轉速為：狀態I：Nh=94.35%,N1=86.56%；狀態II：Nh=92.59%,N1=83.54%。

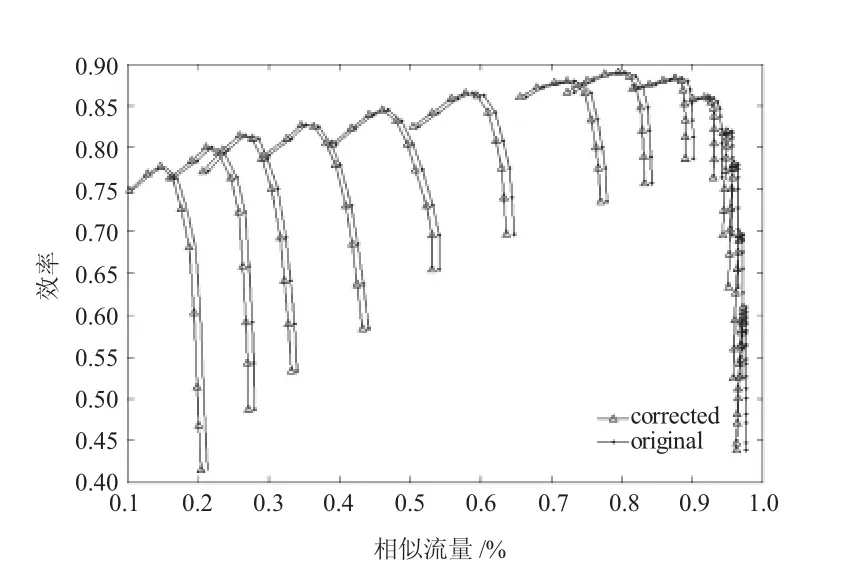
圖4 修正前、后的風扇效率特性

對于這2個狀態，分別基于不同方法得到的部件修正特性，利用粒子群算法進行穩態建模仿真。每種情況分別仿真計算20次，將運算結果對應的適應度函數平均值顯示在表1中。可以看出在不同狀態下的計算結果有較大不同。在狀態I下，用3種方法的修正特性計算所得結果相差不大，本文算法的適應度略小于其他2種方法的，表明本文方法略優。然而對應狀態II，經典方法和曲線擬合方法的計算結果變差，而采用本文方法計算取得最好的結果（適應度最小，表明計算誤差最小）。

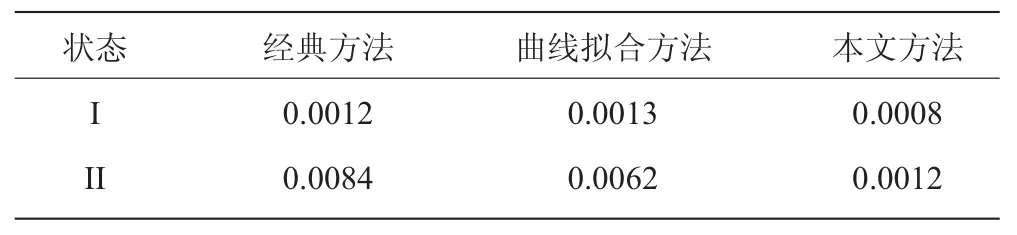
表1 不同狀態下3種方法得到的適應度函數平均值

5 結論

（1）研究了1種更加有效的綜合利用多個狀態試車數據的發動機部件特性修正方法，該方法利用粒子群優化算法分別求得在發動機不同狀態下的修正系數，采用滑動最小二乘方法擬合修正系數曲面，從而得到修正特性。

（2）該方法能夠提高修正精度，優于其他傳統方法，為開展基于單機監控和視情維修提供了準確的部件數據。

[1]Kamboukos P，Mathioudakis K.Comparison of linear and nonlinear gas turbine performance diagnostics[J].Journal of Engineering for Gas Turbines and Power，2005，127（1）：49-56.

[2]Zwebek A，Pilidis P.Degradation effects on combined cycle power plant performance-Part I:gas turbine cycle component degradation effects[J].Journal of Engineering for Gas Turbines and Power，2003，125（7）：651-657.

[3]Li Y G，Nilkitsaranont P.Gas turbine performance prognostic for condition based maintenance[J].Applied Energy，2009，86（10）：2152-2161.

[4]Volponi A J，DePold H，Ganguli R.The use of Kalman filter and neural network methodologies in gas turbine performance diagnostics:a comparative study[J].Journal of Engineering for Gas Turbines and Power，2003，125（7）：917-924.

[5]Fasching W A.CF6 jet engine performance improvement summary report[R].NASA-CR-2165612，1982.

[6]Stamatis A，Mathioudakis K，Papailiou K D.Adaptive simulation of gas turbine performance[J].Journal of Engineering for Gas Turbines and Power，1990，112（2）：168-175.

[7]吳虎，肖洪，蔣建軍.渦扇發動機部件特性自適應模擬[J].推進技術，2005，26（5）：430-433.WU Hu，XIAO Hong，JIANG Jianjun.Adaptive simulation of turbofan engine component performance[J].Journal of Propulsion Technology，2005，26（5）：430-433.（in Chinese）

[8]陳玉春，黃興，徐思遠，等.渦輪發動機部件特性自適應模型的確定方法[J].推進技術，2008，29（2）：214-218.CHEN Yuchun，HUANG Xing，XU Siyuan，et al.A method of definition for the adaptive simulation model of gas turbine performance[J].Journal of Propulsion Technology，2008，29 （2）：214-218.（in Chinese）.

[9]廉小純，吳虎.航空燃氣輪機原理 [M].北京：國防工業出版社，2001：45-74.LIAN Xiaochun，WU Hu.Aviation gas turbine principle[M].Beijing：Defense Industry Press，2001：45-74.（in Chinese）

[10]Kong C，Ki J.A new scaling method for component maps of gas turbine using system identification[J].Journal of Engineering for Gas Turbines and Power，2003，125（1）：958-979.

[11]Li Y G，Pilidis P.GA-based design-point performance adaptation and its comparison with ICM-based approach [J].Applied Energy，2010，87（1）：340-348.

[12]Kennedy J，Eberhart R C.Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks.Perth，Australia，1995：1942-1948.

[13]Eberhart R C，Kennedy J.A new optimizer using particle swarm theory[C]//Proceedings of the Sixth International Symposium on Micro Machine and Human Science，Nagoya:Japan，1995：39-43.

[14]Levin D.The approximation power of moving least-squares[J].Mathematics of Computation，1998，67（10）：1517-1531.

[15]Most T，Bucher C.A moving least squares weighting function for the element-free Galerkin method which almost fulfills essential boundary conditions[J].Structural Engineering and Mechanics，2005，21（3）：315-321.

Research on Correction of Aeroengine Component Characteristics

JIA Zhong-hu1,GUO Wei-gang1,MA Li2
（1.Department of Aircraft Engineering,Naval Aeronautical Engineering Institute,Yantai Shandong 264001,China;2.Navy Customer Representative Office of Engine in Shenyang,Shenyang 110043,China）

Aiming at the problem that the conventional correction methods doesn't consider the multi-condition of engine,the correction of component characteristic based on particle swarm and Moving Least Squares(MLS)was presented.The particle swarm method was used to solve the correction coefficients under different conditions.The MLSmethod was used to fit the curve consisted of correction coefficients,and got the correction coefficients from the orginal characteristic.The experiment results show the proposed method outperforms the conventional methods and improves the accuracy of component characteristic correction,which provide the accurate data for single aircraft monitoring and maintenance.

component characteristic correction;particle swarm algorithms;Moving Least Square method;aeroengine

V231.91

A

10.13477/j.cnki.aeroengine.2015.01.019

2014-01-21

賈忠湖（1964），男，博士，副教授，研究方向為飛行器動力學；E-mail：jiazh586@sina.com。

賈忠湖，郭衛剛，馬力.某型發動機部件特性修正技術研究[J].航空發動機，2015，41（1）:94-98.JIA Zhonghu，GUOWeigang，MA Li.Research on correction of aeroenginecomponentcharacteristics[J].Aeroengine，2015，41（1）：94-98.

（編輯：張寶玲）