加權Dirichlet空間上Toeplitz算子的緊性與Fredholm性質

夏　錦，胡　坤

（廣州大學a.數學與信息科學學院；b.數學與交叉科學廣東普通高校重點實驗室，廣東廣州　510006）

夏錦a，胡坤b

（廣州大學a.數學與信息科學學院；b.數學與交叉科學廣東普通高校重點實驗室，廣東廣州510006）

利用對數加權Bloch空間和對數加權小Bloch空間，刻畫了加權Dirichlet空間上Toeplitz算子的有界性、緊性與Fredholm性質，討論了Toeplitz算子的譜性質，計算了Toeplitz算子的Fredholm指標.

加權Dirichlet空間；Toeplitz算子；緊性；Fredholm指標

1　Introduction and prelim inaries

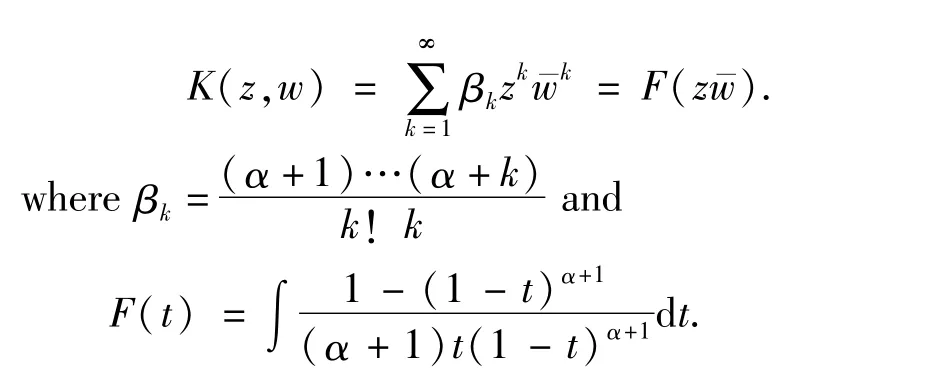
We deal with compactness of Toeplitz，little Hankel and Hankel operators.The results of compactness of these operator on Dirichlet space D2，can be found in CAO［5］，ZHAO［6］.Herewe obtain some useful sufficient condition for compactness of Toeplitz，little Hankel and Hankel operators onOur proof is partly based on some estimates in connection with logarithmic weighted bounded mean oscillation which is similar to bounded mean oscillation in ZHU［3］.More information of Toeplitz operators refers to Refs［7－13］.

2　Bounded and com pact Toeplitz，little Hankel and Hankel operators

We first recall some results on bounded mean oscillation in Bergman metric，more facts and proof in Ref.［2］.

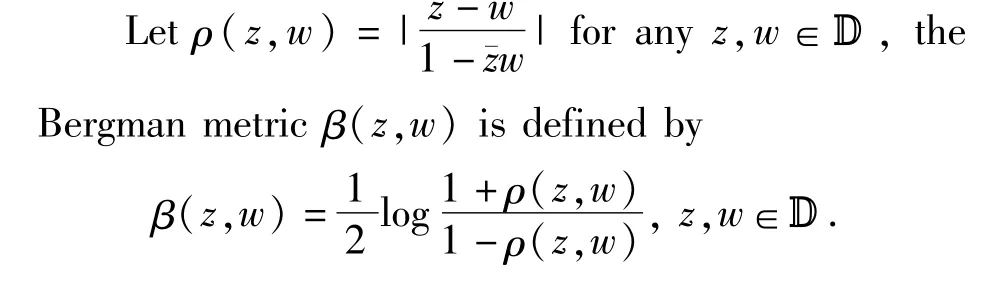
The Bergman metric is also M?bius invariant：

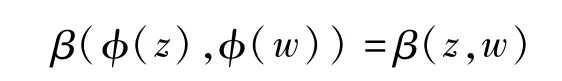
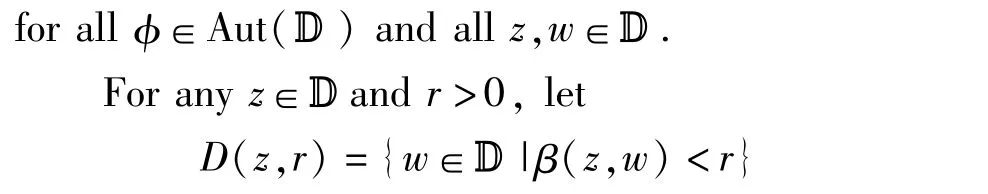
be the Bergman metric disk with center z and radius r.It is well known that D（z，r）is a Euclidean disk with Euclidean center and radius

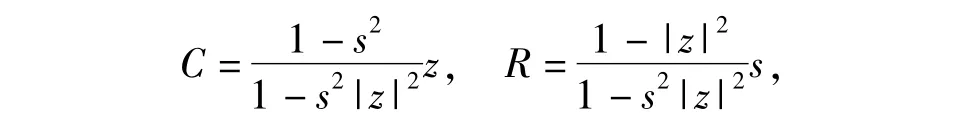
where s＝tanh r∈（0，1）.A functionφ∈L1is called

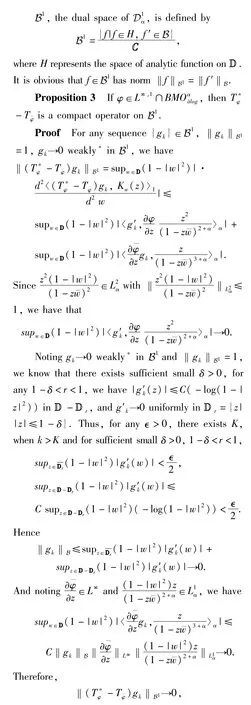
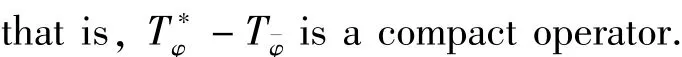
3　Fredholmness and index

A bounded linear operator A on a Banach space X is said to be Fredholm if both its kernel and cokernel are finite-dimensional；the index of a Fredholm operator is defined by

Ind A＝dim ker A－dim coker A.

We also define thewinding number of a nonvanishing continuous function u（z）by

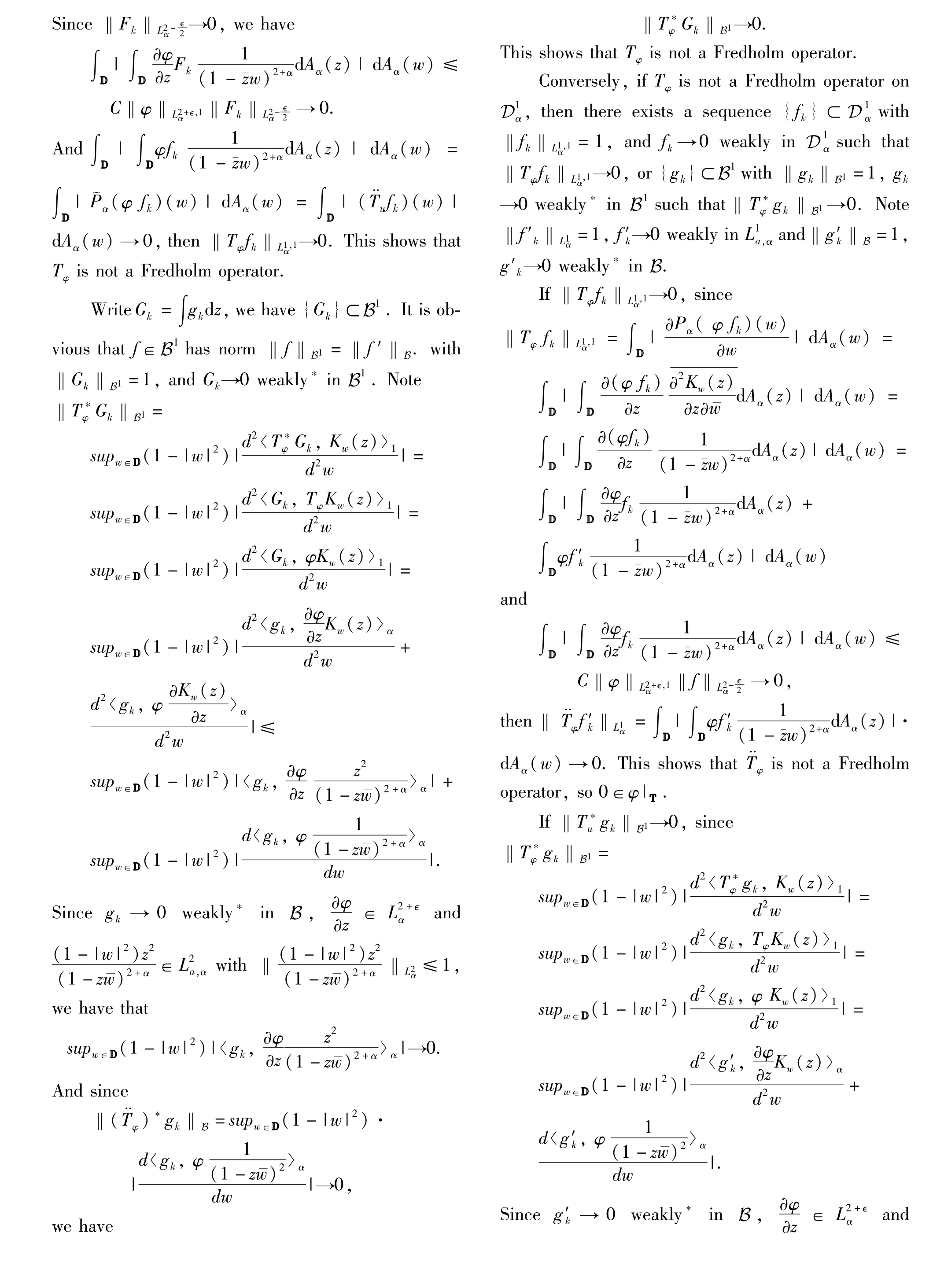
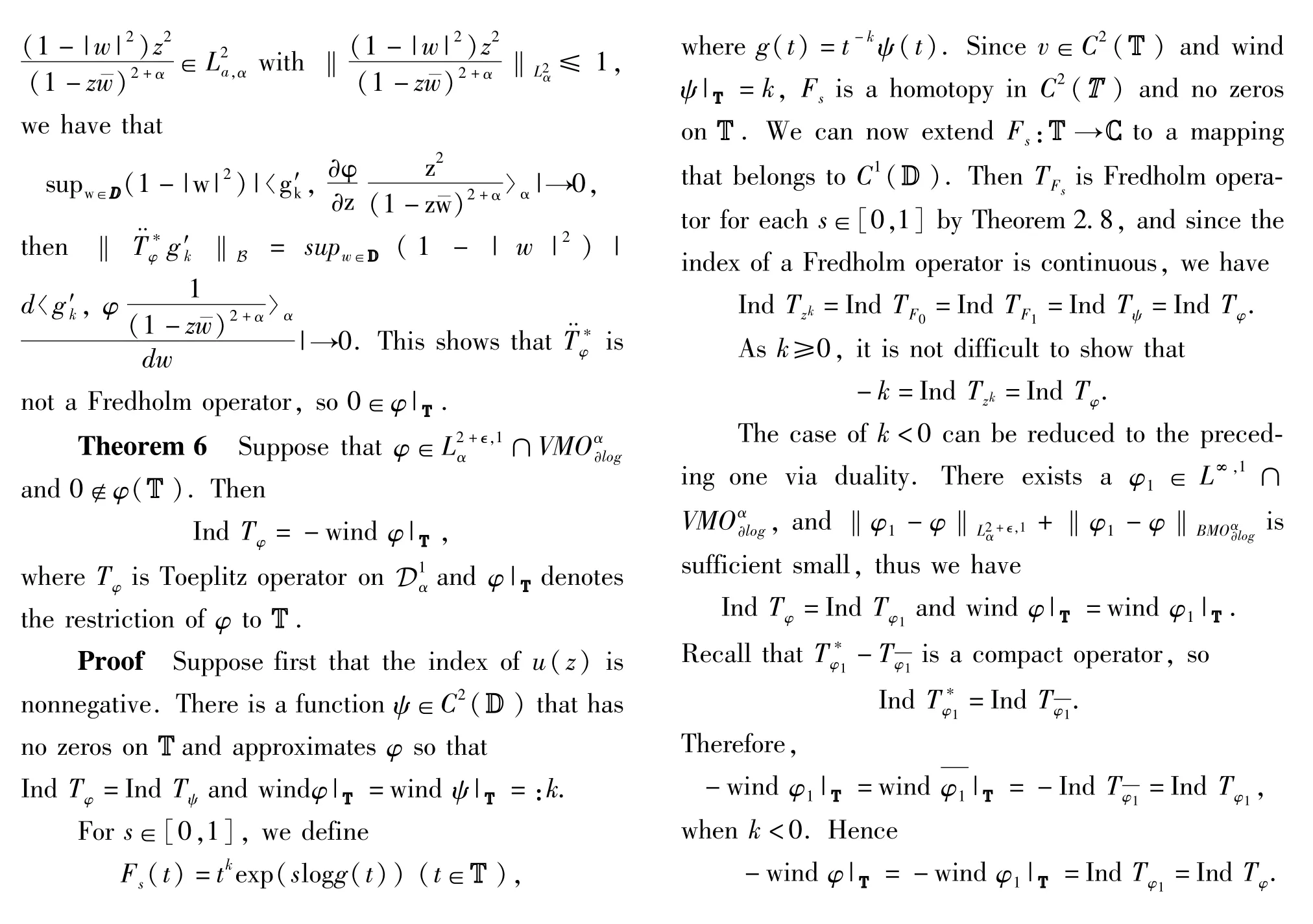
References：

［1］WANG X F，XIA J，CAO G F.Some properties of Toeplitz operators on Dirichlet space Dp［J］.Acta Math Sci，2012，32（2）：395-403.（in Chinese）

［2］ZHU K.Operator Theory on the Function spaces［M］.New York：Marcel Dekker，1990.

［3］ZHU K.Multipliers of BMO in Bergman metrics with applications to Toeplitz operators［J］.J Funct Anal，1989，87（1）：31-50.

［4］TASKINEN J，VIRTANEN JA.Spectral theory of Toeplitz and Hankel operators on the Bergman space A1［J］.New York J Math，2008，34：305-323.

［5］CAO G F.Fredholm properties of Toeplitz operators on Dirichlet spaces［J］.Pacif JMath，1999，2：209-223.

［6］ZHAO L K.Hankel operators on the Dirichlet space［J］.JMath Anal Appl，2009，352：767-772.

［7］B?TTCHER A，SILBERMANN B.Analysis of Toeplitz operators［M］.Berlin：Springer Monographs in Mathematics，Springer-Verlag，2006.

［8］PAPADIMITRAKIS M，VIRTANEN JA.Hankel and Toeplitz transforms on H1：Continuity，compactness and Fredholm properties［J］.Integr Eq Oper Theory，2008，61（4）：573-591.

［9］COBURN L A.Singular integral operators and Toeplitz operators on odd spheres［J］.Indian Univ Math J，1973/1974，23：433-439.

［10］MCDONALD G，SUNDBERG C.Fredholm properties of a class of Toeplitz operators on the ball［J］.Indian Univ Math J，1977，26（3）：567-576.

［11］DOUGLASR G.Banach algebraic techniques in operators theory（vol.128）［M］.New York：Springer-Verlag，1971.

［12］UPMEIER H.Toeplitz operators and index Theory in several complex variables［M］.Basel：Birkh?user，1996.

［13］CAO G F.Toeplitz operators and algebras on Dirichlet spaces［J］.Chin Ann Math，2002，23B（3）：385-396.

【責任編輯：周全】

date：2015－10－20；Revised date：2015－11－09

Com pact and Fredholm Toeplitz operators on weighted Dirichlet space

XIA Jina，HU Kunb

（a.School of Mathematics and Information Sciences；b.Key Laboratory of Mathematics and Interdisciplinary Sciences of the Guangdong Higher Education Institute，Guangzhou University，Guangzhou 510006，China）

In this paper，boundedness and compactness of the Toeplitz operators on the weighted Dirichlit space D1αare characterized with logarithmic weighted Bloch space and little logarithmic weighted Bloch space.The spectra properties of the Toeplitz operators are discussed.The Fredholm index of Toeplitz operators are computed.

weighted Dirichlet space；Toeplitz operator；compactness；Fredholm index

O 177 Document code：A

O 177

A

1671-4229（2015）06-0001-08

Biography：XIA Jin（1973－），female，associate professor，Ph.D.E-mail：2695931921＠qq.com