基于動態規劃的腸衣搭配模型與軟件設計

李 輝

(西南科技大學制造科學與工程學院，四川 綿陽 621010)

1 問題的重述

原料按長度分檔，通常以0.5 米為一檔，如：3-3.4 米按3 米計算，3.5 米-3.9 米按3.5 米計算，其余的依此類推。表1 是幾種常見成品的規格，長度單位為米，∞表示沒有上限，但實際長度小于26 米。

根據以上成品和原料描述，設計一個原料搭配方案，工人根據這個方案“照方抓藥”進行生產。公司對搭配方案的具體要求見2011 年競賽題。

2 問題分析

原問題的本質，是對腸衣原料按成品規格進行組裝的問題。由于所生產的成品有三種規格，并且三種規格所對應的最短長度和最大長度、根數等不相同，因此應該先把原料表分為三種規格的原料表。由于要求充分利用原材料，并且剩余的原材料可以降級使用，因此應該考慮從第三種規格的成品開始組裝，再依次組裝第二種成品、第一種成品。通過上述分析和本文要解決的問題，有以下兩個問題需要解決：

1）窮舉運算量巨大，如何降低問題的規模。成品的組裝，是從符合成品規格的原料中，選擇一組合適的原料，滿足根數、總長度等要求，即得到一個成品（捆），比較容易想到窮舉的辦法。但是，以題目中給出的數據，計算機運算量是巨大的，如何保證給定一組原料數據時，可以在30 分鐘以內給出搭配方案，是建立數學模型要解決的關鍵問題。

2）如何降級處理。例如，當成品三的長度為18 米的原料有剩余時，采用何種方式進行分割的問題。

3 問題的假設

1）以0.5 米為一檔，如：3-3.4 米按3 米計算，因此每一根都是有誤差的。在組裝的過程中，不考慮累積誤差對成品總長度的影響。

2）假設原料描述表中給出的根數和長度數據都是準確的。

4 符號說明

xij——表示第j 種規格的原料放到第i 個成品（捆）的根數；

cj——表示第j種規格原料的總根數；

mj——表示第j種規格原料的長度；

yi——第i 捆是否成為一個成品，0-1 變量，0 表示不能；

n——原料總的規格種數；

w——假設模型可求得的最大捆數，比理論上計算的數據稍大即可；

v——某種規格的成品，每捆所包含的根數。

5 模型建立與求解

問題的實質是根據題中的原料情況，建立適當的數學模型，通過計算，給出合理的搭配方案，以方便工人“照方抓藥”。根據對問題的分析，用0-1 變量yi表示能否組裝成一個成品。我們可以根據題目中給出的數據，計算理論的成品數量。例如，對于符合成品三規格的原料，我們可以求得其總長度為∑mjcj，理論上可以組裝成品的最大捆數為∑mjcj/89，約為136.62 捆，即最大可組裝136 捆。理論上，只要假設的值為137，再通過LINGO 軟件求得到的結果就是最大的成品捆數。

5.1 建立線性規劃模型

基于該思路，我們建立如下的數學模型：

決策變量：xij，表示第j 種規格的原料放到第i 個成品（捆）的根數；

目標函數為：Max=∑yj

約束條件：

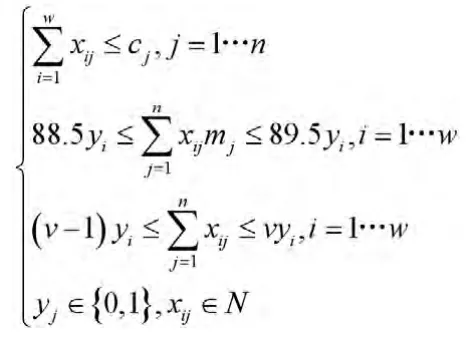
由于三種成品不同規格，因此需要根據上述思路建立三個類似的線性規劃模型。

在實際的計算中我們發現，基于該模型的LINGO 程序在進行成品二和成品三搭配方案的運算時，經過長達9 個小時的計算仍然未能得出結果。而在進行成品一的計算時，LINGO 僅需要1 秒鐘左右的時間。

5.2 建立動態規劃模型

在前面的計算中，我們發現當w——假設模型可求得的最大捆數，它的值取得較小時，LINGO 的運算速度很快，比如取w=10 時，程序運算需要1 秒。此時的最優值，并非原料所能組裝成該種規格的成品的最大捆數，而是從原料中選取了部分，組成了10 捆。

受此啟發，如果不斷的運行該程序，每次僅從原料中選取一部分，組裝成10 捆，把用掉的原料從總的原料中減去，更新庫存。下一次運算時，從上一次剩余的原料中，再選取一部分組裝成10 捆，依次這樣處理下去……直到所剩原料已經不足以組成1 捆（即最優值返回0時）為止，結束運算。

5.3 關于原料降級處理的措施

在上述討論中，我們為了充分利用原料，將剩余的原料做降級處理。拿長度為14 米的材料為例，如果有剩余，它可以和長度介于7-13.5 米的進行捆扎，成品屬于7-13.5 米的規格經過分析，大概分為以下三種措施：

①直接降至下一級的最大長度。如將剩余14 米長度的原料，割成13.5 米，即從成品三的原料變成成品二的原料，并且是成品二的最大長度。采用這樣的降級處理辦法，操作簡單，程序設計中容易實現，但是對原料浪費比較大。

②對半分割。觀察三種規格的成品的原料長度，可以發現，上一級剩余的原料，無論長度是多少，對半分割后都能落在下一級的長度區間內。采用這樣的降級處理辦法，操作簡單，程序設計也容易實現，比第一種辦法更節約原料。

③按一定的尺寸，將其分割成不相等的兩段或者兩段以上。根據組裝過程中所缺少某種長度的原料，將剩余原料切成該種長度的原料。例如，在對成品三的組裝中，14 米長的原料有剩余。在下一階段，對成品二的組裝中，11 米的原料緊缺，即將14 米的原料切成11+3米，11 米的降到下一級使用，3 米的降到再下一級使用。這樣的降級處理辦法看似比較科學，但是在動態規劃過程中，很難得到哪種原料緊缺的數據。因此，在實際操作中比較困難。

5.4 利用EXCEL 和LINGO 開發腸衣搭配軟件

如果單純依靠LINGO 軟件逐步進行求解，每進行一次運算，都要對矩陣xij中的數據進行分析，統計每一種長度的原料用掉了多少根，并計算剩余多少根，更新庫存。接著，修改LINGO 程序中的數據，再次進行運算。在對成品三的計算中，xij變量的個數達到10×24 個，統計起來很繁瑣，容易出錯，并且需要較為專業的人員才能看懂LINGO 的結果報告，不便于公司的應用。

為了使操作更加簡單有效，我們將腸衣原料數據輸入到excel 電子表格中，并在LINGO 中使用excel 表格的數據，將每次運行LINGO程序的結果返回給excel 電子表格的指定區域。配合使用VBA 和宏，對每次運算結果進行整理，統計用掉的原料根數、更新庫存量，并把搭配方案以“藥方”的形式通過二維表反饋給用戶，用戶界面如圖1 所示。

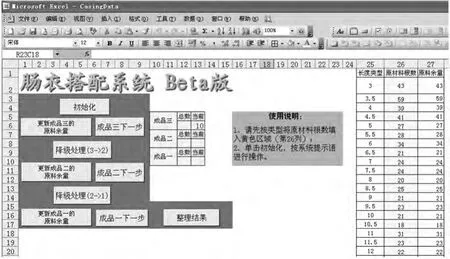
圖1 系統用戶界面

在圖1 所示的“腸衣搭配系統Beta 版”中，通過編寫VBA 程序，將每次運行LINGO 得到的數據進行統計分析，更新原料余量，所有操作都轉化為簡單的鼠標操作。下面對具體的操作做簡單的說明。

①打開名為“CasingData.xls”的EXCEL 電子表格；

②將原料描述表的數據，對應輸入第26 列；

③單擊初始化；

④按彈出對話框的提示，打開LINGO 程序，求解名為“階段三”的LINGO 程序，如圖2 所示；求解完成后，切換到excel 窗口；

⑤單擊“更新成品三原料余量”，可以看到在EXCEL 窗口的右邊，已經有了10 種搭配方案；

⑥單擊“成品三下一步”，按提示切換到LINGO 窗口，再次求解。求解完成后，切換到excel 窗口；注意，雖然這里求解的都是名為“階段三”的LINGO 程序，但EXCEL 傳遞給LINGO 的參數已經改變，因此運算結果是不一樣的。

⑦單擊“更新成品三原料余量”，新的搭配方案已經追加到上一步方案的后面；

⑧當成品三的原料再也不能組裝成品時，系統會提示采取降級處理。單擊“降級處理(3-＞2)”，系統提示運行“階段二”的LINGO 程序；

⑨同理，直至程序將成品一的原料搭配完成，提示“第一種規格的成品分配方案運算完畢，搭配完成！”時，表示運算已結束；

⑩單擊“整理結果”，EXCEL 窗口的右邊，方案已經給出，即是給工人的“藥方”，成品一的部分捆數的搭配表如表1 所示，其它捆的“藥方”形式也如表1 類似。

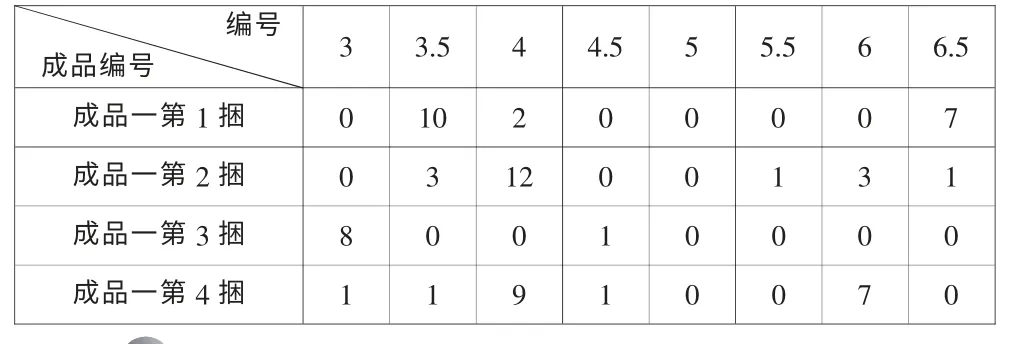
表1 成品一搭配表

［1］教材編寫組，編.運籌學[M].3 版.北京：清華大學出版社，2005，6.

［2］謝金星，薛毅.優化模型與LINGO/lindo 軟件[M].北京：清華大學出版社，2007.